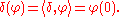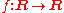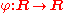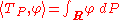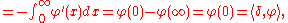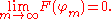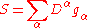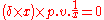Distribution (mathematics)
Encyclopedia
In mathematical analysis
, distributions (or generalized functions) are objects that generalize function
s. Distributions make it possible to differentiate
functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used to formulate generalized solutions of partial differential equation
s. Where a classical solution may not exist or be very difficult to establish, a distribution solution to a differential equation is often much easier. Distributions are also important in physics
and engineering
where many problems naturally lead to differential equations whose solutions or initial conditions are distributions, such as the Dirac delta distribution.
Generalized functions were introduced by Sergei Sobolev
in 1935. They were re-introduced in the late 1940s by Laurent Schwartz
, who developed a comprehensive theory of distributions.
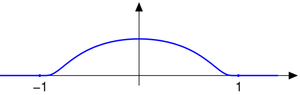Distributions are a class of linear functional
s that map a set of test functions (conventional and well-behaved
functions) onto the set of real numbers. In the simplest case, the set of test functions considered is D(R), which is the set of functions from R to R having two properties:
Then, a distribution d is a linear mapping from D(R) to R. Instead of writing d(φ), where φ is a test function in D(R), it is conventional to write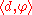
. A simple example of a distribution is the Dirac delta δ, defined by
There are straightforward mappings from both locally integrable function
s and probability distribution
s to corresponding distributions, as discussed below. However, not all distributions can be formed in this manner.
Suppose that
is a locally integrable function
, and let
be a test function in D(R). We can then define a corresponding distribution Tf by:
This integral is a real number
which linearly and continuously
depends on φ. This suggests the requirement that a distribution should be linear and continuous over the space of test functions D(R), which completes the definition. In a conventional abuse of notation
, f may be used to represent both the original function f and the distribution Tf derived from it.
Similarly, if P is a probability distribution
on the reals and φ is a test function, then a corresponding distribution TP may be defined by:
Again, this integral continuously and linearly depends on φ, so that TP is in fact a distribution.
Such distributions may be multiplied with real numbers and can be added together, so they form a real vector space
. In general it is not possible to define a multiplication for distributions, but distributions may be multiplied with infinitely differentiable functions.
It's desirable to choose a definition for the derivative of a distribution which, at least for distributions derived from locally integrable functions, has the property that (Tf)' = Tf . If φ is a test function, we can show that
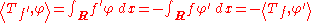
using integration by parts
and noting that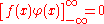
, since φ is zero outside of a bounded set. This suggests that if S is a distribution, we should define its derivative S' by
It turns out that this is the proper definition; it extends the ordinary definition of derivative, every distribution becomes infinitely differentiable and the usual properties of derivatives hold.
Example: Recall that the Dirac delta (so-called Dirac delta function) is the distribution defined by
It is the derivative of the distribution corresponding to the Heaviside step function
H: For any test function φ,
so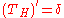
. Note, 
because of compact support. Similarly, the derivative of the Dirac delta is the distribution
This latter distribution is our first example of a distribution which is derived from neither a function nor a probability distribution.
U of Rn will be formally defined. With minor modifications, one can also define complex-valued distributions, and one can replace Rn by any (paracompact) smooth manifold.
The first object to define is the space D(U) of test functions on U. Once this is defined, it is then necessary to equip it with a topology
by defining the limit of a sequence
of elements of D(U). The space of distributions will then be given as the space of continuous linear functionals on D(U).
subset K of U such that φ(x) = 0 for all x in U \ K. The elements of D(U) are the infinitely differentiable functions φ : U → R with compact support – also known as bump functions. This is a real vector space
. It can be given a topology
by defining the limit of a sequence
of elements of D(U). A sequence (φk) in D(U) is said to converge to φ ∈ D(U) if the following two conditions hold :
With this definition, D(U) becomes a complete locally convex topological vector space
satisfying the Heine–Borel property
. If Ui is a countable nested family of open subsets of U with compact closures
, then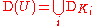
where DKi is the set of all smooth functions with support lying in Ki. The topology on D(U) is the final topology
of the family of nested metric spaces DKi and so D(U) is an LF-space
. The topology is not metrizable by the Baire category theorem
, since D(U) is the union of subspaces of the first category in D(U) .
S : D(U) → R (or S : D(U) → C), such that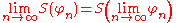
for any convergent sequence φn in D(U). The space of all distributions on U is denoted by D'(U). Equivalently, the vector space D'(U) is the continuous dual space of the topological vector space D(U).
The dual pairing between a distribution S in D′(U) and a test function 'φ' in D(U) is denoted using angle brackets thus:
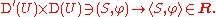
Equipped with the weak-* topology, the space D'(U) is a locally convex topological vector space. In particular, a sequence (Sk) in D'(U) converges to a distribution S if and only if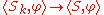
for all test functions φ. This is the case if and only if Sk converges uniformly to S on all bounded subsets of D(U). (A subset E of D(U) is bounded if there exists a compact subset K of U and numbers dn such that every φ in E has its support in K and has its n-th derivatives bounded by dn.)
over every compact subset K of U. This is a large class of functions which includes all continuous functions and all Lp functions
. The topology on D(U) is defined in such a fashion that any locally integrable function ƒ yields a continuous linear functional on D(U) – that is, an element of D′(U) – denoted here by Tƒ, whose value on the test function φ is given by the Lebesgue integral:
Conventionally, one abuses notation
by identifying Tƒ with ƒ, provided no confusion can arise, and thus the pairing between ƒ and φ is often written
If ƒ and g are two locally integrable functions, then the associated distributions Tƒ and Tg are equal to the same element of D'(U) if and only if ƒ and g are equal almost everywhere
(see, for instance). In a similar manner, every Radon measure
μ on U defines an element of D'(U) whose value on the test function φ is ∫φ dμ. As above, it is conventional to abuse notation and write the pairing between a Radon measure μ and a test function φ as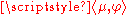
. Conversely, essentially by the Riesz representation theorem
, every distribution which is non-negative on non-negative functions is of this form for some (positive) Radon measure.
The test functions are themselves locally integrable, and so define distributions. As such they are dense in D'(U) with respect to the topology on D'(U) in the sense that for any distribution S ∈ D'(U), there is a sequence φn ∈ D(U) such that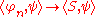
for all ψ ∈ D(U). This follows at once from the Hahn–Banach theorem
, since by an elementary fact about weak topologies the dual of D'(U) with its weak-* topology is the space D(U) . This can also be proven more constructively by a convolution argument.
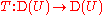
is a linear mapping of vector spaces which is continuous with respect to the weak-* topology, then it is possible to extend T to a mapping
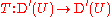
by passing to the limit. (This approach works for more general non-linear mappings as well, provided they are assumed to be uniformly continuous.)
In practice, however, it is more convenient to define operations on distributions by means of the transpose (or adjoint transformation) . If T : D(U) → D(U) is a continuous linear operator, then the transpose is an operator T* : D(U) → D(U) such that
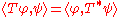
for all φ, ψ ∈ D(U). If such an operator T* exists, and is continuous, then the original operator T may be extended to distributions by defining
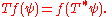
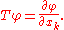
By integration by parts, if φ and ψ are in D(U), then
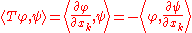
so that T* = −T. This is a continuous linear transformation D(U) → D(U). So, if S ∈ D'(U) is a distribution, then the partial derivative of S with respect to the coordinate xk is defined by the formula
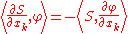
for all test functions 'φ'. In this way, every distribution is infinitely differentiable, and the derivative in the direction xk is a linear operator on D′(U). In general, if α = (α1, ..., αn) is an arbitrary multi-index and ∂α denotes the associated mixed partial derivative operator, the mixed partial derivative ∂αS of the distribution S ∈ D′(U) is defined by
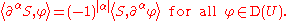
Differentiation of distributions is a continuous operator on D'(U); this is an important and desirable property that is not shared by most other notions of differentiation.
for φ ∈ D(U). Then, for any test function ψ
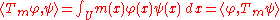
so that Tm* = Tm. Multiplication of a distribution S by the smooth function m is therefore defined by
Under multiplication by smooth functions, D'(U) is a module
over the ring
C∞(U). With this definition of multiplication by a smooth function, the ordinary product rule of calculus remains valid. However, a number of unusual identities also arise.
For example, the Dirac delta distribution δ is defined on R by
〈δ, φ〉 = φ(0),
so that mδ = m(0)δ. Its derivative is given by〈δ', φ〉 = −〈δ, φ〉 = −φ(0). But the product mδ' of m and δ' is the distribution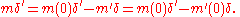
This definition of multiplication also makes it possible to define the operation of a linear differential operator
with smooth coefficients on a distribution. A linear differential operator takes a distribution S ∈ D'(U) to another distribution given by a sum of the form
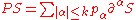
where the coefficients pα are smooth functions in U. If P is a given differential operator, then the minimum integer k for which such an expansion holds for every distribution S is called the order of P. The transpose of P is given by
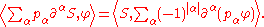
The space D'(U) is a D-module
with respect to the action of the ring of linear differential operators.
, it is possible to define
This is the composition of the distribution S with F, and is also called the pullback of S along F, sometimes written
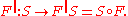
The pullback is often denoted F*, but this notation risks confusion with the above use of '*' to denote the transpose of a linear mapping.
The condition that F be a submersion is equivalent to the requirement that the Jacobian
derivative dF(x) of F is a surjective linear map for every x ∈ V. A necessary (but not sufficient) condition for extending F# to distributions is that F be an open mapping . The inverse function theorem
ensures that a submersion satisfies this condition.
If F is a submersion, then F# is defined on distributions by finding the transpose map. Uniqueness of this extension is guaranteed since F# is a continuous linear operator on D(U). Existence, however, requires using the change of variables
formula, the inverse function theorem (locally) and a partition of unity argument; see .
In the special case when F is a diffeomorphism
from an open subset V of Rn onto an open subset U of Rn change of variables under the integral gives
In this particular case, then, F# is defined by the transpose formula:
.
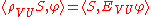
for all test functions φ ∈ D(V).
Unless U = V, the restriction to V is neither injective nor surjective. Lack of surjectivity follows since distributions can blow up towards the boundary of V. For instance, if U = R and V = (0,2), then the distribution
is in D'(V) but admits no extension to D'(U).
of the restriction map ρVU. Explicitly S vanishes on V if
for all test functions φ ∈ C∞(U) with support in V. Let V be a maximal open set on which the distribution S vanishes; i.e., V is the union of every open set on which S vanishes. The support of S is the complement of V in U. Thus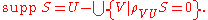
The distribution S has compact support if its support is a compact set. Explicitly, S has compact support if there is a compact subset K of U such that for every test function φ whose support is completely outside of K, we have S(φ) = 0. Compactly supported distributions define continuous linear functions on the space C∞(U); the topology on C∞(U) is defined such that a sequence of test functions φk converges to 0 if and only if all derivatives of φk converge uniformly to 0 on every compact subset of U. Conversely, it can be shown that every continuous linear functional on this space defines a distribution of compact support.
in generality: all tempered distributions have a Fourier transform, but not all distributions have one.
The space of test functions employed here, the so-called Schwartz space S(Rn), is the function space of all infinitely differentiable functions that are rapidly decreasing at infinity along with all partial derivatives. Thus is in the Schwartz space provided that any derivative of φ, multiplied with any power of |x|, converges towards 0 for |x| → ∞. These functions form a complete topological vector space
with a suitably defined family of seminorms. More precisely, let
for α, β multi-indices of size n. Then φ is a Schwartz function if all the values
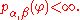
The family of seminorms pα, β defines a locally convex topology on the Schwartz-space. The seminorms are, in fact, norms
on the Schwartz space, since Schwartz functions are smooth. The Schwartz space is metrizable and complete
. Because the Fourier transform changes differentiation by xα into multiplication by xα and vice-versa, this symmetry implies that the Fourier transformations of a Schwartz function is also a Schwartz function.
The space of tempered distributions is defined as the (continuous) dual
of the Schwartz space. In other words, a distribution F is a tempered distribution if and only if
is true whenever,
holds for all multi-indices α, β.
The derivative of a tempered distribution is again a tempered distribution. Tempered distributions generalize the bounded (or slow-growing) locally integrable functions; all distributions with compact support and all square-integrable functions are tempered distributions. All locally integrable functions ƒ with at most polynomial growth, i.e. such that ƒ(x) = O(|x|r) for some r, are tempered distributions. This includes all functions in Lp(Rn)
for p ≥ 1.
The tempered distributions can also be characterized as slowly growing. This characterization is dual to the rapidly falling behaviour, e.g.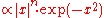
, of the test functions.
To study the Fourier transform, it is best to consider complex-valued test functions and complex-linear distributions. The ordinary continuous Fourier transform
F yields then an automorphism
of Schwartz function space, and we can define the Fourier transform of the tempered distribution S by (FS)(ψ) = S(Fψ) for every test function ψ. FS is thus again a tempered distribution. The Fourier transform is a continuous, linear, bijective operator from the space of tempered distributions to itself. This operation is compatible with differentiation in the sense that
and also with convolution: if S is a tempered distribution and ψ is a slowly increasing infinitely differentiable function on Rn (meaning that all derivatives of ψ grow at most as fast as polynomial
s), then Sψ is again
a tempered distribution and
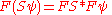
is the convolution of FS and Fψ. In particular, the Fourier transform of the unity function is the δ distribution.
of a function with a distribution, or even the convolution of two distributions.
Convolution of a test function with a distribution
If ƒ ∈ D(Rn) is a compactly supported smooth test function, then convolution with ƒ defines an operator
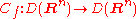
defined by Cƒg = ƒ∗g, which is linear (and continuous
with respect to the LF space topology on D(Rn).)
Convolution of ƒ with a distribution S ∈ D′(Rn) can be defined by taking the transpose of Cƒ relative to the duality pairing of D(Rn) with the space D′(Rn) of distributions . If ƒ, g, 'φ' ∈ D(Rn), then by Fubini's theorem
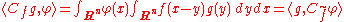
where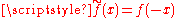
. Extending by continuity, the convolution of ƒ with a distribution S is defined by
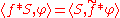
for all test functions 'φ' ∈ D(Rn).
An alternative way to define the convolution of a function ƒ and a distribution S is to use the translation operator τx defined on test functions by
and extended by the transpose to distributions in the obvious way . The convolution of the compactly supported function ƒ and the distribution S is then the function defined for each x ∈ Rn by
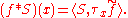
It can be shown that the convolution of a compactly supported function and a distribution is a smooth function. If the distribution S has compact support as well, then ƒ∗S is a compactly supported function, and the Titchmarsh convolution theorem
implies that
where ch denotes the convex hull
.
Distribution of compact support
It is also possible to define the convolution of two distributions S and T on Rn, provided one of them has compact support. Informally, in order to define S∗T where T has compact support, the idea is to extend the definition of the convolution ∗ to a linear operation on distributions so that the associativity formula
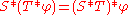
continues to hold for all test-functions 'φ'. proves the uniqueness of such an extension.
It is also possible to provide a more explicit characterization of the convolution of distributions . Suppose that it is T that has compact support. For any test function 'φ' in D(Rn), consider the function
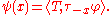
It can be readily shown that this defines a smooth function of x, which moreover has compact support. The convolution of S and T is defined by
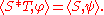
This generalizes the classical notion of convolution
of functions and is compatible with differentiation in the following sense:
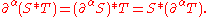
This definition of convolution remains valid under less restrictive assumptions about S and T; see for instance and .
Tempered distributions
If ƒ ∈ S′(Rn) is a tempered distribution, then there exists a constant C > 0, and positive integers M and N such that for all Schwartz functions φ ∈S(Rn)
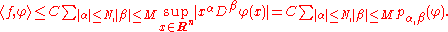
This estimate along with some techniques from functional analysis can be used to show that there is a continuous slowly increasing function F and a multiindex α such that
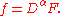
Compactly supported distributions
Let U be an open set, and K a compact subset of U. If ƒ is a distribution supported on K, then there is a continuous function F compactly supported in U (possibly on a larger set than K itself) such that
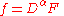
for some multi-index α. This follows from the previously quoted result on tempered distributions by means of a localization argument.
Distributions with point support
If ƒ has support at a single point {P}, then ƒ is in fact a finite linear combination of distributional derivatives of the δ function at P. That is, there exists an integer m and complex constants aα for multi indices |α| ≤ m such that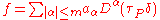
where τP is the translation operator.
General distributions
A version of the above theorem holds locally in the following sense . Let S be a distribution on U. Then one can find for every multi-index α a continuous function gα such that
and that any compact subset K of U intersects the supports of only finitely many gα; therefore, to evaluate the value of S for a given smooth function f compactly supported in U, we only need finitely many gα; hence the infinite sum above is well-defined as a distribution. If the distribution S is of finite order, then one can choose gα in such a way that only finitely many of them are nonzero.
, in which spaces of holomorphic function
s are used as test functions. A refined theory has been developed, in particular Mikio Sato
's algebraic analysis
, using sheaf theory and several complex variables
. This extends the range of symbolic methods that can be made into rigorous mathematics, for example Feynman integrals
.
in the 1950s. For example, if p.v. 1/x is the distribution obtained by the Cauchy principal value
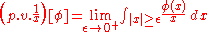
for all φ ∈ S(R), and δ is the Dirac delta distribution then
but
so the product of a distribution by a smooth function (which is always well defined) cannot be extended to an associative
product on the space of distributions.
Thus, nonlinear problems cannot be posed in general and thus not solved within distribution theory alone.
In the context of quantum field theory
, however, solutions can be found. In more than two spacetime dimensions the problem is related to the regularization
of divergences
. Here Henri Epstein and Vladimir Glaser developed the mathematically rigorous (but extremely technical) causal perturbation theory
. This does not solve the problem in other situations. Many other interesting theories are non linear, like for example Navier-Stokes equations
of fluid dynamics
.
In view of this, several not entirely satisfactory theories of algebra
s of generalized function
s have been developed, among which Colombeau's (simplified) algebra
is maybe the most popular in use today.
A simple solution of the multiplication problem is dictated by the path integral formulation
of quantum mechanics
. Since this is required to be equivalent to the Schrödinger theory of quantum mechanics
which is invariant under coordinate transformations, this property must be shared by path integrals. This fixes all products of distributions as shown by . The result is equivalent to what can be derived from dimensional regularization
.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, distributions (or generalized functions) are objects that generalize function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. Distributions make it possible to differentiate
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative. Distributions are widely used to formulate generalized solutions of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. Where a classical solution may not exist or be very difficult to establish, a distribution solution to a differential equation is often much easier. Distributions are also important in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
where many problems naturally lead to differential equations whose solutions or initial conditions are distributions, such as the Dirac delta distribution.
Generalized functions were introduced by Sergei Sobolev
Sergei Lvovich Sobolev
Sergei Lvovich Sobolev was a Soviet mathematician working in mathematical analysis and partial differential equations. He was born in St. Petersburg, and died in Moscow.-Work:...
in 1935. They were re-introduced in the late 1940s by Laurent Schwartz
Laurent Schwartz
Laurent-Moïse Schwartz was a French mathematician. He pioneered the theory of distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields medal in 1950 for his work...
, who developed a comprehensive theory of distributions.
Basic idea
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s that map a set of test functions (conventional and well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
functions) onto the set of real numbers. In the simplest case, the set of test functions considered is D(R), which is the set of functions from R to R having two properties:
- The function is smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
(infinitely differentiable); - The function has compact support (is identically zero outside some interval).
Then, a distribution d is a linear mapping from D(R) to R. Instead of writing d(φ), where φ is a test function in D(R), it is conventional to write
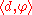. A simple example of a distribution is the Dirac delta δ, defined by
There are straightforward mappings from both locally integrable function
Locally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
s and probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s to corresponding distributions, as discussed below. However, not all distributions can be formed in this manner.
Suppose that
is a locally integrable function
Locally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
, and let
be a test function in D(R). We can then define a corresponding distribution Tf by:
-
.
This integral is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
which linearly and continuously
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
depends on φ. This suggests the requirement that a distribution should be linear and continuous over the space of test functions D(R), which completes the definition. In a conventional abuse of notation
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
, f may be used to represent both the original function f and the distribution Tf derived from it.
Similarly, if P is a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on the reals and φ is a test function, then a corresponding distribution TP may be defined by:
Again, this integral continuously and linearly depends on φ, so that TP is in fact a distribution.
Such distributions may be multiplied with real numbers and can be added together, so they form a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. In general it is not possible to define a multiplication for distributions, but distributions may be multiplied with infinitely differentiable functions.
It's desirable to choose a definition for the derivative of a distribution which, at least for distributions derived from locally integrable functions, has the property that (Tf)' = Tf . If φ is a test function, we can show that
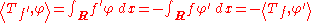
using integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
and noting that
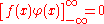, since φ is zero outside of a bounded set. This suggests that if S is a distribution, we should define its derivative S' by-
.
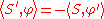It turns out that this is the proper definition; it extends the ordinary definition of derivative, every distribution becomes infinitely differentiable and the usual properties of derivatives hold.
Example: Recall that the Dirac delta (so-called Dirac delta function) is the distribution defined by
It is the derivative of the distribution corresponding to the Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
H: For any test function φ,
so
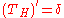. Note, because of compact support. Similarly, the derivative of the Dirac delta is the distributionThis latter distribution is our first example of a distribution which is derived from neither a function nor a probability distribution.
Test functions and distributions
In the sequel, real-valued distributions on an open subsetOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U of Rn will be formally defined. With minor modifications, one can also define complex-valued distributions, and one can replace Rn by any (paracompact) smooth manifold.
The first object to define is the space D(U) of test functions on U. Once this is defined, it is then necessary to equip it with a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
by defining the limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of elements of D(U). The space of distributions will then be given as the space of continuous linear functionals on D(U).
Test function space
The space D(U) of test functions on U is defined as follows. A function φ : U → R is said to have compact support if there exists a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset K of U such that φ(x) = 0 for all x in U \ K. The elements of D(U) are the infinitely differentiable functions φ : U → R with compact support – also known as bump functions. This is a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. It can be given a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
by defining the limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of elements of D(U). A sequence (φk) in D(U) is said to converge to φ ∈ D(U) if the following two conditions hold :
- There is a compact set K ⊂ U containing the supports of all φk:
-
- For each multiindex α, the sequence of partial derivatives Dαφk tends uniformly to Dαφ.
With this definition, D(U) becomes a complete locally convex topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
satisfying the Heine–Borel property
Heine–Borel theorem
In the topology of metric spaces the Heine–Borel theorem, named after Eduard Heine and Émile Borel, states:For a subset S of Euclidean space Rn, the following two statements are equivalent:*S is closed and bounded...
. If Ui is a countable nested family of open subsets of U with compact closures
, then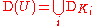where DKi is the set of all smooth functions with support lying in Ki. The topology on D(U) is the final topology
Final topology
In general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
of the family of nested metric spaces DKi and so D(U) is an LF-space
LF-space
In mathematics, an LF-space is a topological vector space V that is a countable strict inductive limit of Fréchet spaces. This means that for each n there is a subspace V_n such that-Properties:...
. The topology is not metrizable by the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
, since D(U) is the union of subspaces of the first category in D(U) .
Distributions
A distribution on U is a linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
S : D(U) → R (or S : D(U) → C), such that
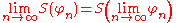
for any convergent sequence φn in D(U). The space of all distributions on U is denoted by D'(U). Equivalently, the vector space D'(U) is the continuous dual space of the topological vector space D(U).
The dual pairing between a distribution S in D′(U) and a test function 'φ' in D(U) is denoted using angle brackets thus:
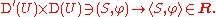
Equipped with the weak-* topology, the space D'(U) is a locally convex topological vector space. In particular, a sequence (Sk) in D'(U) converges to a distribution S if and only if
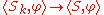
for all test functions φ. This is the case if and only if Sk converges uniformly to S on all bounded subsets of D(U). (A subset E of D(U) is bounded if there exists a compact subset K of U and numbers dn such that every φ in E has its support in K and has its n-th derivatives bounded by dn.)
Functions as distributions
The function ƒ : U → R is called locally integrable if it is Lebesgue integrableLebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
over every compact subset K of U. This is a large class of functions which includes all continuous functions and all Lp functions
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. The topology on D(U) is defined in such a fashion that any locally integrable function ƒ yields a continuous linear functional on D(U) – that is, an element of D′(U) – denoted here by Tƒ, whose value on the test function φ is given by the Lebesgue integral:
Conventionally, one abuses notation
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
by identifying Tƒ with ƒ, provided no confusion can arise, and thus the pairing between ƒ and φ is often written
If ƒ and g are two locally integrable functions, then the associated distributions Tƒ and Tg are equal to the same element of D'(U) if and only if ƒ and g are equal almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
(see, for instance). In a similar manner, every Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
μ on U defines an element of D'(U) whose value on the test function φ is ∫φ dμ. As above, it is conventional to abuse notation and write the pairing between a Radon measure μ and a test function φ as
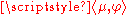. Conversely, essentially by the Riesz representation theoremRiesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, every distribution which is non-negative on non-negative functions is of this form for some (positive) Radon measure.
The test functions are themselves locally integrable, and so define distributions. As such they are dense in D'(U) with respect to the topology on D'(U) in the sense that for any distribution S ∈ D'(U), there is a sequence φn ∈ D(U) such that
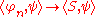
for all ψ ∈ D(U). This follows at once from the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, since by an elementary fact about weak topologies the dual of D'(U) with its weak-* topology is the space D(U) . This can also be proven more constructively by a convolution argument.
Operations on distributions
Many operations which are defined on smooth functions with compact support can also be defined for distributions. In general, if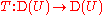is a linear mapping of vector spaces which is continuous with respect to the weak-* topology, then it is possible to extend T to a mapping
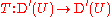
by passing to the limit. (This approach works for more general non-linear mappings as well, provided they are assumed to be uniformly continuous.)
In practice, however, it is more convenient to define operations on distributions by means of the transpose (or adjoint transformation) . If T : D(U) → D(U) is a continuous linear operator, then the transpose is an operator T* : D(U) → D(U) such that
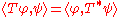
for all φ, ψ ∈ D(U). If such an operator T* exists, and is continuous, then the original operator T may be extended to distributions by defining
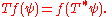
Differentiation
If T : D(U) → D(U) is given by the partial derivative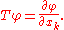By integration by parts, if φ and ψ are in D(U), then
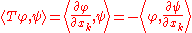
so that T* = −T. This is a continuous linear transformation D(U) → D(U). So, if S ∈ D'(U) is a distribution, then the partial derivative of S with respect to the coordinate xk is defined by the formula
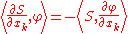
for all test functions 'φ'. In this way, every distribution is infinitely differentiable, and the derivative in the direction xk is a linear operator on D′(U). In general, if α = (α1, ..., αn) is an arbitrary multi-index and ∂α denotes the associated mixed partial derivative operator, the mixed partial derivative ∂αS of the distribution S ∈ D′(U) is defined by
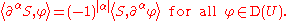
Differentiation of distributions is a continuous operator on D'(U); this is an important and desirable property that is not shared by most other notions of differentiation.
Multiplication by a smooth function
If m : U → R is an infinitely differentiable function and S is a distribution on U, then the product mS is defined by (mS)(φ) = S(mφ) for all test functions φ. This definition coincides with the transpose transformation offor φ ∈ D(U). Then, for any test function ψ
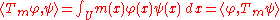
so that Tm* = Tm. Multiplication of a distribution S by the smooth function m is therefore defined by
Under multiplication by smooth functions, D'(U) is a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
C∞(U). With this definition of multiplication by a smooth function, the ordinary product rule of calculus remains valid. However, a number of unusual identities also arise.
For example, the Dirac delta distribution δ is defined on R by
〈δ, φ〉 = φ(0),
so that mδ = m(0)δ. Its derivative is given by〈δ', φ〉 = −〈δ, φ〉 = −φ(0). But the product mδ' of m and δ' is the distribution
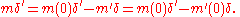
This definition of multiplication also makes it possible to define the operation of a linear differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
with smooth coefficients on a distribution. A linear differential operator takes a distribution S ∈ D'(U) to another distribution given by a sum of the form
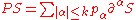
where the coefficients pα are smooth functions in U. If P is a given differential operator, then the minimum integer k for which such an expansion holds for every distribution S is called the order of P. The transpose of P is given by
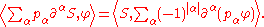
The space D'(U) is a D-module
D-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
with respect to the action of the ring of linear differential operators.
Composition with a smooth function
Let S be a distribution on an open set U ⊂ Rn. Let V be an open set in Rn, and F : V → U. Then provided F is a submersionSubmersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
, it is possible to define
This is the composition of the distribution S with F, and is also called the pullback of S along F, sometimes written
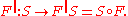
The pullback is often denoted F*, but this notation risks confusion with the above use of '*' to denote the transpose of a linear mapping.
The condition that F be a submersion is equivalent to the requirement that the Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
derivative dF(x) of F is a surjective linear map for every x ∈ V. A necessary (but not sufficient) condition for extending F# to distributions is that F be an open mapping . The inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
ensures that a submersion satisfies this condition.
If F is a submersion, then F# is defined on distributions by finding the transpose map. Uniqueness of this extension is guaranteed since F# is a continuous linear operator on D(U). Existence, however, requires using the change of variables
Integration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
formula, the inverse function theorem (locally) and a partition of unity argument; see .
In the special case when F is a diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
from an open subset V of Rn onto an open subset U of Rn change of variables under the integral gives
In this particular case, then, F# is defined by the transpose formula:
Localization of distributions
There is no way to define the value of a distribution in D'(U) at a particular point of U. However, as is the case with functions, distributions on U restrict to give distributions on open subsets of U. Furthermore, distributions are locally determined in the sense that a distribution on all of U can be assembled from a distribution on an open cover of U satisfying some compatibility conditions on the overlap. Such a structure is known as a sheafSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
.
Restriction
Let U and V be open subsets of Rn with V ⊂ U. Let EVU : D(V) → D(U) be the operator which extends by zero a given smooth function compactly supported in V to a smooth function compactly supported in the larger set U. Then the restriction mapping ρ VU is defined to be the transpose of EVU. Thus for any distribution S ∈ D'(U), the restriction ρVU S is a distribution in the dual space D'(V) defined by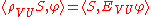for all test functions φ ∈ D(V).
Unless U = V, the restriction to V is neither injective nor surjective. Lack of surjectivity follows since distributions can blow up towards the boundary of V. For instance, if U = R and V = (0,2), then the distribution
is in D'(V) but admits no extension to D'(U).
Support of a distribution
Let S ∈ D′(U) be a distribution on an open set U. Then S is said to vanish on an open set V of U if S lies in the kernelKernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of the restriction map ρVU. Explicitly S vanishes on V if
for all test functions φ ∈ C∞(U) with support in V. Let V be a maximal open set on which the distribution S vanishes; i.e., V is the union of every open set on which S vanishes. The support of S is the complement of V in U. Thus
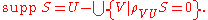
The distribution S has compact support if its support is a compact set. Explicitly, S has compact support if there is a compact subset K of U such that for every test function φ whose support is completely outside of K, we have S(φ) = 0. Compactly supported distributions define continuous linear functions on the space C∞(U); the topology on C∞(U) is defined such that a sequence of test functions φk converges to 0 if and only if all derivatives of φk converge uniformly to 0 on every compact subset of U. Conversely, it can be shown that every continuous linear functional on this space defines a distribution of compact support.
Tempered distributions and Fourier transform
By using a larger space of test functions, one can define the tempered distributions, a subspace of D'(Rn). These distributions are useful if one studies the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
in generality: all tempered distributions have a Fourier transform, but not all distributions have one.
The space of test functions employed here, the so-called Schwartz space S(Rn), is the function space of all infinitely differentiable functions that are rapidly decreasing at infinity along with all partial derivatives. Thus is in the Schwartz space provided that any derivative of φ, multiplied with any power of |x|, converges towards 0 for |x| → ∞. These functions form a complete topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
with a suitably defined family of seminorms. More precisely, let
for α, β multi-indices of size n. Then φ is a Schwartz function if all the values
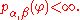
The family of seminorms pα, β defines a locally convex topology on the Schwartz-space. The seminorms are, in fact, norms
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on the Schwartz space, since Schwartz functions are smooth. The Schwartz space is metrizable and complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
. Because the Fourier transform changes differentiation by xα into multiplication by xα and vice-versa, this symmetry implies that the Fourier transformations of a Schwartz function is also a Schwartz function.
The space of tempered distributions is defined as the (continuous) dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of the Schwartz space. In other words, a distribution F is a tempered distribution if and only if
is true whenever,
holds for all multi-indices α, β.
The derivative of a tempered distribution is again a tempered distribution. Tempered distributions generalize the bounded (or slow-growing) locally integrable functions; all distributions with compact support and all square-integrable functions are tempered distributions. All locally integrable functions ƒ with at most polynomial growth, i.e. such that ƒ(x) = O(|x|r) for some r, are tempered distributions. This includes all functions in Lp(Rn)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for p ≥ 1.
The tempered distributions can also be characterized as slowly growing. This characterization is dual to the rapidly falling behaviour, e.g.
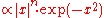, of the test functions.To study the Fourier transform, it is best to consider complex-valued test functions and complex-linear distributions. The ordinary continuous Fourier transform
Continuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
F yields then an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of Schwartz function space, and we can define the Fourier transform of the tempered distribution S by (FS)(ψ) = S(Fψ) for every test function ψ. FS is thus again a tempered distribution. The Fourier transform is a continuous, linear, bijective operator from the space of tempered distributions to itself. This operation is compatible with differentiation in the sense that
and also with convolution: if S is a tempered distribution and ψ is a slowly increasing infinitely differentiable function on Rn (meaning that all derivatives of ψ grow at most as fast as polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s), then Sψ is again
a tempered distribution and
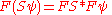
is the convolution of FS and Fψ. In particular, the Fourier transform of the unity function is the δ distribution.
Convolution
Under some circumstances, it is possible to define the convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of a function with a distribution, or even the convolution of two distributions.
Convolution of a test function with a distribution
If ƒ ∈ D(Rn) is a compactly supported smooth test function, then convolution with ƒ defines an operator
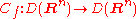
defined by Cƒg = ƒ∗g, which is linear (and continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
with respect to the LF space topology on D(Rn).)
Convolution of ƒ with a distribution S ∈ D′(Rn) can be defined by taking the transpose of Cƒ relative to the duality pairing of D(Rn) with the space D′(Rn) of distributions . If ƒ, g, 'φ' ∈ D(Rn), then by Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
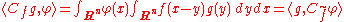
where
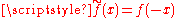. Extending by continuity, the convolution of ƒ with a distribution S is defined by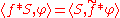for all test functions 'φ' ∈ D(Rn).
An alternative way to define the convolution of a function ƒ and a distribution S is to use the translation operator τx defined on test functions by
and extended by the transpose to distributions in the obvious way . The convolution of the compactly supported function ƒ and the distribution S is then the function defined for each x ∈ Rn by
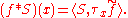
It can be shown that the convolution of a compactly supported function and a distribution is a smooth function. If the distribution S has compact support as well, then ƒ∗S is a compactly supported function, and the Titchmarsh convolution theorem
Titchmarsh convolution theorem
The Titchmarsh convolution theorem is named after Edward Charles Titchmarsh,a British mathematician. The theorem describes the properties of the support of the convolution of two functions.- Titchmarsh convolution theorem :...
implies that
where ch denotes the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
.
Distribution of compact support
It is also possible to define the convolution of two distributions S and T on Rn, provided one of them has compact support. Informally, in order to define S∗T where T has compact support, the idea is to extend the definition of the convolution ∗ to a linear operation on distributions so that the associativity formula
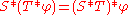
continues to hold for all test-functions 'φ'. proves the uniqueness of such an extension.
It is also possible to provide a more explicit characterization of the convolution of distributions . Suppose that it is T that has compact support. For any test function 'φ' in D(Rn), consider the function
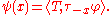
It can be readily shown that this defines a smooth function of x, which moreover has compact support. The convolution of S and T is defined by
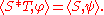
This generalizes the classical notion of convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of functions and is compatible with differentiation in the following sense:
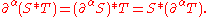
This definition of convolution remains valid under less restrictive assumptions about S and T; see for instance and .
Distributions as derivatives of continuous functions
The formal definition of distributions exhibits them as a subspace of a very large space, namely the topological dual of D(U) (or S(Rd) for tempered distributions). It is not immediately clear from the definition how exotic a distribution might be. To answer this question, it is instructive to see distributions built up from a smaller space, namely the space of continuous functions. Roughly, any distribution is locally a (multiple) derivative of a continuous function. A precise version of this result, given below, holds for distributions of compact support, tempered distributions, and general distributions. Generally speaking, no proper subset of the space of distributions contains all continuous functions and is closed under differentiation. This says that distributions are not particularly exotic objects; they are only as complicated as necessary.Tempered distributions
If ƒ ∈ S′(Rn) is a tempered distribution, then there exists a constant C > 0, and positive integers M and N such that for all Schwartz functions φ ∈S(Rn)
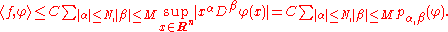
This estimate along with some techniques from functional analysis can be used to show that there is a continuous slowly increasing function F and a multiindex α such that
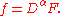
Compactly supported distributions
Let U be an open set, and K a compact subset of U. If ƒ is a distribution supported on K, then there is a continuous function F compactly supported in U (possibly on a larger set than K itself) such that
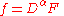
for some multi-index α. This follows from the previously quoted result on tempered distributions by means of a localization argument.
Distributions with point support
If ƒ has support at a single point {P}, then ƒ is in fact a finite linear combination of distributional derivatives of the δ function at P. That is, there exists an integer m and complex constants aα for multi indices |α| ≤ m such that
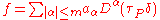
where τP is the translation operator.
General distributions
A version of the above theorem holds locally in the following sense . Let S be a distribution on U. Then one can find for every multi-index α a continuous function gα such that
and that any compact subset K of U intersects the supports of only finitely many gα; therefore, to evaluate the value of S for a given smooth function f compactly supported in U, we only need finitely many gα; hence the infinite sum above is well-defined as a distribution. If the distribution S is of finite order, then one can choose gα in such a way that only finitely many of them are nonzero.
Using holomorphic functions as test functions
The success of the theory led to investigation of the idea of hyperfunctionHyperfunction
In mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...
, in which spaces of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s are used as test functions. A refined theory has been developed, in particular Mikio Sato
Mikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
's algebraic analysis
Algebraic analysis
Algebraic analysis is an area of mathematics that deals with systems of linear partial differential equations by using sheaf theory and complex analysis to study properties and generalizations of functions such as hyperfunctions and microfunctions.-See also:...
, using sheaf theory and several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. This extends the range of symbolic methods that can be made into rigorous mathematics, for example Feynman integrals
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
.
Problem of multiplication
A possible limitation of the theory of distributions (and hyperfunctions) is that it is a purely linear theory, in the sense that the product of two distributions cannot consistently be defined (in general), as has been proved by Laurent SchwartzLaurent Schwartz
Laurent-Moïse Schwartz was a French mathematician. He pioneered the theory of distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields medal in 1950 for his work...
in the 1950s. For example, if p.v. 1/x is the distribution obtained by the Cauchy principal value
Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
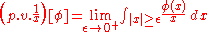
for all φ ∈ S(R), and δ is the Dirac delta distribution then
but
so the product of a distribution by a smooth function (which is always well defined) cannot be extended to an associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
product on the space of distributions.
Thus, nonlinear problems cannot be posed in general and thus not solved within distribution theory alone.
In the context of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, however, solutions can be found. In more than two spacetime dimensions the problem is related to the regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
of divergences
Ultraviolet divergence
In physics, an ultraviolet divergence is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very high energy , or, equivalently, because of physical phenomena at very short distances. An infinite answer to a question that should have a...
. Here Henri Epstein and Vladimir Glaser developed the mathematically rigorous (but extremely technical) causal perturbation theory
Causal perturbation theory
Causal perturbation theory is a mathematically rigorous approach to renormalization theory, which makesit possible to put the theoretical setup of perturbative quantum field theory on a sound mathematical basis....
. This does not solve the problem in other situations. Many other interesting theories are non linear, like for example Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
of fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
.
In view of this, several not entirely satisfactory theories of algebra
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
s of generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s have been developed, among which Colombeau's (simplified) algebra
Colombeau algebra
In mathematics, the Colombeau algebra is an algebra introduced with the aim of constructing an improved theory of distributions in which multiplication is not problematic...
is maybe the most popular in use today.
A simple solution of the multiplication problem is dictated by the path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Since this is required to be equivalent to the Schrödinger theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
which is invariant under coordinate transformations, this property must be shared by path integrals. This fixes all products of distributions as shown by . The result is equivalent to what can be derived from dimensional regularization
Dimensional regularization
In theoretical physics, dimensional regularization is a method introduced by Giambiagi and Bollini for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of an auxiliary complex parameter d, called the...
.
See also
- CurrentCurrent (mathematics)In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz...
- Colombeau algebraColombeau algebraIn mathematics, the Colombeau algebra is an algebra introduced with the aim of constructing an improved theory of distributions in which multiplication is not problematic...
- Gelfand triple
- Generalized functionGeneralized functionIn mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
- Homogeneous distribution
- HyperfunctionHyperfunctionIn mathematics, hyperfunctions are generalizations of functions, as a 'jump' from one holomorphic function to another at a boundary, and can be thought of informally as distributions of infinite order...
- Malgrange–Ehrenpreis theoremMalgrange–Ehrenpreis theoremIn mathematics, the Malgrange–Ehrenpreis theorem states that every non-zero linear differential operator with constant coefficients has a Green's function...
- Pseudodifferential operator
- Riesz representation theoremRiesz representation theoremThere are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
- Vague topologyVague topologyIn mathematics, particularly in the area of functional analysis and topological vector spaces, the vague topology is an example of the weak-* topology which arises in the study of measures on locally compact Hausdorff spaces....
- Weak solutionWeak solutionIn mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
Further reading
- M. J. Lighthill (1959). Introduction to Fourier Analysis and Generalised Functions. Cambridge University Press. ISBN 0-521-09128-4 (requires very little knowledge of analysis; defines distributions as limits of sequences of functions under integrals)
- H. KleinertHagen KleinertHagen Kleinert is Professor of Theoretical Physics at the Free University of Berlin, Germany , at theWest University of Timişoara, at thein Bishkek. He is also of the...
, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2006)(also available online here). See Chapter 11 for defining products of distributions from the physical requirement of coordinate invariance. - V.S. Vladimirov (2002). Methods of the theory of generalized functions. Taylor & Francis. ISBN 0-415-27356-0.....