Antiderivative

	Email		Print
	Bookmark		Link

Antiderivative

In calculus

Calculus

Calculus is a branch of mathematics that includes the study of limit , derivatives, integrals, and infinite series, and constitutes a major part of modern university education....
, an antiderivative, primitive or indefinite integral of a function

Function (mathematics)

The mathematical concept of a function expresses dependence between two quantities, one of which is known and the other which is produced. A function associates a single output to each input element drawn from a fixed Set , such as the real numbers , although different inputs may have the same output....
f is a function F whose derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much a quantity is changing at a given point....
is equal to f, i.e., F ′ = f. The process of solving for antiderivatives is antidifferentiation (or indefinite integration). Antiderivatives are related to definite integral

Integral

Integration is an important concept in mathematics, specifically in the field of calculus and, more broadly, mathematical analysis. Given a function ƒ of a Real number variable x and an interval [a, b] of the real line, the integral...
s through the fundamental theorem of calculus

Fundamental theorem of calculus

The fundamental theorem of calculus specifies the relationship between the two central operations of calculus: derivative and integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an antiderivative can be reversed by a differentiation....
: the definite integral of a function over an interval is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval.
ntidifferentiation is the process of finding the set of all antiderivatives of a given function.

Discussion

Ask a question about 'Antiderivative'

Start a new discussion about 'Antiderivative'

Answer questions from other users

Full Discussion Forum

Encyclopedia

In calculus

Calculus

Function (mathematics)

Derivative

Integral

Fundamental theorem of calculus

Rules and Formula

Antidifferentiation is the process of finding the set of all antiderivatives of a given function. The symbol denotes the operation of antidifferentiation, and we write

where

and

The expression F(x) + C is the general antiderivative of f.

Because antidifferentiation is the inverse operation of the differentiation, antidifferentiation theorems and rules are obtained from those on differentiation. Thus the following theorems can be proved from the corresponding differentiation theorems:

General antidifferentiation rule:

The general antiderivative of a constant times a function is the constant multiplied by the general antiderivative of the function:

If f and g are defined on the same interval, then:

The general antiderivative of the sum or difference of two functions equals the sum or difference of the general antiderivatives of the functions.

If are defined on the same interval,

where are constants.

If n is a rational number,

Forms containing Trigonometric Functions

Forms containing Inverse Trigonometric Functions

Forms containing Exponential and Logarithmic Functions

Forms containing Hyperbolic Functions

Example

The function F(x) = x³/3 is an antiderivative of f(x) = x². As the derivative of a constant is zero

0 (number)

0 is both a number and the numerical digit used to represent that number in numeral system. It plays a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures....
, x² will have an infinite

Infinity

Infinity comes from the Latin infinitas or "unboundedness." It refers to several distinct concepts – usually linked to the idea of "without end" – which arise in philosophy, mathematics, and theology....
number of antiderivatives; such as (x³/3) + 0, (x³ / 3) + 7, (x³ / 3) − 42, etc. Thus, the entire antiderivative family

Family (mathematics)

Family in mathematics may refer to:*Indexed family*Family of sets...
of x² can be obtained by changing the value of C in F(x) = (x³ / 3) + C; where C is an arbitrary constant known as the constant of integration

Arbitrary constant of integration

In calculus, the indefinite integral of a given function is always written with a constant, the constant of integration. This constant expresses an ambiguity inherent in the construction of antiderivatives....
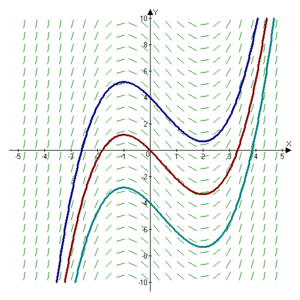
. Essentially, the graphs

Graph of a function

In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian coordinate system, together with Cartesian axes, etc....
of antiderivatives of a given function are vertical translation

Vertical translation

In function graph of a function, a vertical translation is a Relation graph which, for every Point ; has a y value which differs from another graph, by exactly some constant c....
s of each other; each graph's location depending upon the value

Value (mathematics)

In mathematics, value commonly refers to the 'output' of a Function . In the most basic case, that of unary, single-valued functions, there is one input and one output .The function of the example is real-valued, since each and every possible function value is real....
of C.

Uses and properties

Antiderivatives are important because they can be used to compute definite integrals

Integral

Fundamental theorem of calculus

The fundamental theorem of calculus specifies the relationship between the two central operations of calculus: derivative and integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an antiderivative can be reversed by a differentiation....
: if F is an antiderivative of the integrable function f, then:

Because of this, each of the infinitely many antiderivatives of a given function f is sometimes called the "general integral" or "indefinite integral" of f and is written using the integral symbol with no bounds:

If F is an antiderivative of f, and the function f is defined on some interval

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set....
, then every other antiderivative G of f differs from F by a constant: there exists a number C such that G(x) = F(x) + C for all x. C is called the arbitrary constant of integration

Arbitrary constant of integration

Disjoint union

In set theory, a disjoint union is a modified union operation which indexes the elements according to which set they originated in.Formally, let be a family of sets indexed by I....
of two or more intervals, then a different constant of integration may be chosen for each of the intervals. For instance

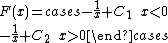
is the most general antiderivative of on its natural domain

Every continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, small changes in the input result in small changes in the output. Otherwise, a function is said to be discontinuous....
f has an antiderivative, and one antiderivative F is given by the definite integral of f with variable upper boundary: Varying the lower boundary produces other antiderivatives (but not necessarily all possible antiderivatives). This is another formulation of the fundamental theorem of calculus

Fundamental theorem of calculus

Polynomial

In mathematics, a polynomial is an expression constructed from variables and constants, using the operations of addition, subtraction, multiplication, and constant non-negative whole number exponents....
s, exponential function

Exponential function

The exponential function is a function in mathematics. The application of this function to a value x is written as exp. Equivalently, this can be written in the form ex, where e is the mathematical constant that is the base of the natural logarithm and that is also known as Euler's number....
s, logarithm

Logarithm

In mathematics, the logarithm of a number to a given base is the Power or exponent to which the base must be raised in order to produce the number....
s, trigonometric functions, inverse trigonometric functions and their combinations). Examples of these are

See also differential Galois theory

Differential Galois theory

In mathematics, the antiderivatives of certain elementary functions cannot themselves be expressed as elementary functions. A standard example of such a function is e−x2, whose antiderivative is the error function, familiar from statistics....
for a more detailed discussion.

Techniques of integration

Finding antiderivatives of elementary functions is often considerably harder than finding their derivatives. For some elementary functions, it is impossible to find an antiderivative in terms of other elementary functions. See the article on elementary functions

Elementary function (differential algebra)

In mathematics, an elementary function is a function built from a finite number of exponential functions, logarithms, constants, one variable, and nth roots through function composition and combinations using the four arithmetic ....
for further information.

We have various methods at our disposal:

the linearity of integration
Linearity of integration

In calculus, linearity is a fundamental property of the integral that follows from the sum rule in integration and the constant factor rule in integration....
allows us to break complicated integrals into simpler ones
integration by substitution
Integration by substitution

In calculus, integration by substitution is a tool for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative....
, often combined with trigonometric identities or the natural logarithm
Natural logarithm

The natural logarithm, formerly known as the hyperbolic logarithm, is the logarithm to the base e , where e is an irrational number constant approximately equal to 2.718281828....
integration by parts
Integration by parts

In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other, hopefully simpler, integrals....
to integrate products of functions
the inverse chain rule method, a special case of integration by substitution
the method of partial fractions in integration
Partial fractions in integration

In integral calculus, the use of partial fractions is required to integrate the general rational function. Any rational function of a real variable can be written as the sum of a polynomial function and a finite number of partial fractions....
allows us to integrate all rational function
Rational function

In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions....
s (fractions of two polynomials)
the Risch algorithm
Risch algorithm

The Risch algorithm, named after Robert H. Risch, is an algorithm for the calculus operation of indefinite integration . The algorithm transforms the problem of integration into a problem in differential algebra....
integrals can also be looked up in a table of integrals
when integrating multiple times, we can use certain additional techniques, see for instance double integrals and polar coordinates
Coordinates (mathematics)

Coordinates are numbers which describe the location of points in a plane or in space. For example, the height above sea level is a coordinate which is useful for describing points near the surface of the earth....
, the Jacobian
Jacobian

In vector calculus, the Jacobian is shorthand for either the Jacobian matrix or its determinant, the Jacobian determinant.In algebraic geometry the Jacobian of a algebraic curve means the Jacobian variety: a group variety associated to the curve, in which the curve can be embedded....
and the Stokes' theorem
Stokes' theorem

In differential geometry, Stokes' theorem is a statement about the integral of differential forms which generalizes several theorems from vector calculus....
computer algebra system
Computer algebra system

A computer algebra system is a Application software that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form....
s can be used to automate some or all of the work involved in the symbolic techniques above, which is particularly useful when the algebraic manipulations involved are very complex or lengthy
if a function has no elementary antiderivative (for instance, exp(x²)), its definite integral can be approximated using numerical integration
Numerical integration

In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical ordinary differential equations....
to calculate the ( times) repeated antiderivative of a function Cauchy's formula is useful (cf. Cauchy formula for repeated integration
Cauchy formula for repeated integration

The Cauchy formula for repeated integration allows one to compress antidifferentiations of a function into a single integral ....
):

Antiderivatives of non-continuous functions

To illustrate some of the subtleties of the fundamental theorem of calculus

Fundamental theorem of calculus

The fundamental theorem of calculus specifies the relationship between the two central operations of calculus: derivative and integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an antiderivative can be reversed by a differentiation....
, it is instructive to consider what kinds of non-continuous functions might have antiderivatives. While there are still open questions in this area, it is known that:

Some highly pathological functions
Pathological (mathematics)

In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive.Often, when the usefulness of a theorem is challenged by counterexamples, defenders of the theorem argue that the exceptions are pathological....
with large sets of discontinuities may nevertheless have antiderivatives.
In some cases, the antiderivatives of such pathological functions may be found by Riemann integration
Riemann integral

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an Interval ....
, while in other cases these functions are not Riemann integrable.

We first state some general facts and then provide some illustrative examples. Throughout, we assume that the domains of our functions are open intervals.

A necessary, but not sufficient, condition for a function f to have an antiderivative is that f have the intermediate value property
Intermediate value theorem

In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the of a continuous function there is a corresponding value in its domain mapping to the original....
. That is, if [a,b] is a subinterval of the domain of f and d is any real number between f(a) and f(b), then f(c)=d for some c between a and b. To see this, let F be an antiderivative of f and consider the continuous function g(x)=F(x)-dx on the closed interval [a, b]. Then g must have either a maximum or minimum c in the open interval (a,b) and so 0=g′(c)=f(c)-d.
The set of discontinuities of f must be a meagre set
Baire space

In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes....
. This set must also be an F-sigma set (since the set of discontinuities of any function must be of this type). Moreover for any meagre F-sigma set, one can construct some function f having an antiderivative, which has the given set as its set of discontinuities.
If f has an antiderivative, is bounded
Boundedness

Boundedness or bounded may refer to:*Bounded set, a set of finite size, including a bounded poset, a partially ordered set which has both a greatest element and a least element...
on closed finite subintervals of the domain and has a set of discontinuities of Lebesgue measure
Lebesgue measure

In mathematics, the Lebesgue measure, named after Henri Lebesgue, is the standard way of assigning a length, area or volume to subsets of Euclidean space....
0, then an antiderivative may be found by integration.
If f has an antiderivative F on a closed interval [a,b], then for any choice of partition 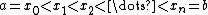, if one chooses sample points 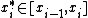as specified by the mean value theorem
Mean value theorem

In calculus, the mean value theorem states, roughly, that given a section of a Smooth function curve, there is at least one point on that section at which the derivative of the curve is equal to the "average" derivative of the section....
, then the corresponding Riemann sum telescopes
Telescoping series

In mathematics, a telescoping series is an informal expression referring to a series whose sum can be found by exploiting the circumstance that nearly every term cancels with either a succeeding or preceding term....
to the value F(b)-F(a).

However if f is unbounded, or if f is bounded but the set of discontinuities of f has positive Lebesgue measure, a different choice of sample points may give a significantly different value for the Riemann sum, no matter how fine the partition. See Example 4 below.

Some examples

The function

with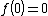 is not continuous at but has the antiderivative

with . Since f is bounded on closed finite intervals and is only discontinuous at 0, the antiderivative F may be obtained by integration: .
The function

with is not continuous at but has the antiderivative

with . Unlike Example 1, f(x) is unbounded in any interval containing 0, so the Riemann integral is undefined.
If f(x) is the function in Example 1 and F is its antiderivative, and is a dense
Dense set

In topology and related areas of mathematics, a subset A of a topological space X is called dense if, intuitively, any point in X can be "well-approximated" by points in A....
countable subset of the open interval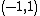 , then the function

has as antiderivative

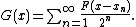
The set of discontinuities of g is precisely the set . Since g is bounded on closed finite intervals and the set of discontinuities has measure 0, the antiderivative G may be found by integration.
Let be a dense countable subset of the open interval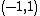 . Consider the everywhere continuous strictly increasing function

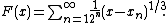
It can be shown that

for all values x where the series converges, and that the graph of F(x) has vertical tangent lines at all other values of x. In particular the graph has vertical tangent lines at all points in the set .

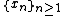Moreover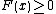 for all x where the derivative is defined. It follows that the inverse function is differentiable everywhere and that

for all x in the set which is dense in the interval 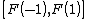. Thus g has an antiderivative G. On the other hand, it can not be true that

since for any partition of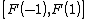 , one can choose sample points for the Riemann sum from the set 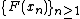, giving a value of 0 for the sum. It follows that g has a set of discontinuities of positive Lebesgue measure. Figure 1 on the right shows an approximation to the graph of g(x) where and the series is truncated to 8 terms. Figure 2 shows the graph of an approximation to the antiderivative G(x), also truncated to 8 terms. On the other hand if the Riemann integral is replaced by the Lebesgue integral, then Fatou's lemma
Fatou's lemma

In mathematics, Fatou's lemma establishes an inequality relating the integral of the limit superior and limit inferior of a sequence of function s to the limit inferior of integrals of these functions....
or the dominated convergence theorem
Dominated convergence theorem

In measure theory, a branch of mathematical analysis, Henri Lebesgue's dominated convergence theorem provides sufficient conditions under which two Limit commute, namely Lebesgue integral and pointwise convergence for a sequence of Function ....
shows that g does satisfy the fundamental theorem of calculus in that context.

In Examples 3 and 4, the sets of discontinuities of the functions g are dense only in a finite open interval . However these examples can be easily modified so as to have sets of discontinuities which are dense on the entire real line . Let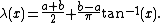 Then has a dense set of discontinuities on and has antiderivative

Using a similar method as in Example 5, one can modify g in Example 4 so as to vanish at all rational numbers. If one uses a naive version of the Riemann integral
Riemann integral

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an Interval ....
defined as the limit of left-hand or right-hand Riemann sums over regular partitions, one will obtain that the integral of such a function g over an interval is 0 whenever a and b are both rational, instead of . Thus the fundamental theorem of calculus will fail spectacularly.