
Hyperreal number
Encyclopedia
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal
quantities. The hyperreals, or nonstandard reals, *R, are an extension
of the real number
s R that contains numbers greater than anything of the form

Such a number is infinite, and its inverse is infinitesimal
. According to Keisler
(1994), the term "hyperreal" was introduced by Edwin Hewitt
(1948, p. 74), who spelled it with a hyphen: "hyper-real".
The hyperreal numbers satisfy the transfer principle
, which is a mathematical implementation of Leibniz's heuristic Law of Continuity
. The transfer principle states that true first order
statements about R are also valid in *R. For example, the commutative law of addition, x + y = y + x, holds for the hyperreals just as it does for the reals; since R is a real closed field
, so is *R. Since sin πn = 0 for all integers n, one also has sin πH = 0 for all hyperinteger
s H. The transfer principle for ultrapowers is a consequence of Łoś' theorem of 1955.
Concerns about the logical soundness
of arguments involving infinitesimals date back to ancient Greek mathematics, with Euclid
replacing such proofs with ones using other techniques such as the method of exhaustion
. In the 1960s Abraham Robinson
proved that the hyperreals were logically consistent if and only if the reals were. This put to rest the fear that any proof involving infinitesimals might be unsound, provided that they were manipulated according to the logical rules which Robinson delineated.
The application of hyperreal numbers and in particular the transfer principle to problems of analysis
is called non-standard analysis
; some find it more intuitive than standard real analysis
. One immediate application is the definition of the basic concepts of analysis such as derivative and integral in a direct fashion, without passing via logical complications of multiple quantifiers. Thus, the derivative of f(x) becomes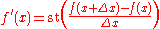 for an infinitesimal
for an infinitesimal 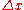 , where st(·) denotes the standard part function
, where st(·) denotes the standard part function
, which associates to every finite hyperreal, the unique real infinitely close to it.
. However, statements of the form "for any set of numbers S ..." may not carry over. The only properties that differ between the reals and the hyperreals are those that rely on quantification over sets, or other higher-level structures such as functions and relations, which are typically constructed out of sets. Each real set, function, and relation has its natural hyperreal extension, satisfying the same first-order properties. The kinds of logical sentences that obey this restriction on quantification are referred to as statements in first-order logic
.
The transfer principle, however, doesn't mean that R and *R have identical behavior. For instance, in *R there exists an element ω such that
but there is no such number in R. This is possible because the existence of such a number cannot be expressed as a first order statement.
As an example of the transfer principle, the statement that for any nonzero number x, 2x ≠ x, is true for the real numbers, and it is in the form required by the transfer principle, so it is also true for the hyperreal numbers. This shows that it is not possible to use a generic symbol such as ∞ for all the infinite quantities in the hyperreal system; infinite quantities differ in magnitude from other infinite quantities, and infinitesimals from other infinitesimals.
Similarly, the casual use of 1/0 = ∞ is invalid, since the transfer principle applies to the statement that division by zero is undefined. The rigorous counterpart of such a calculation would be that if ε is infinitesimal, then 1/ε is infinite.
For any finite hyperreal number x, its standard part, st x, is defined as the unique real number that differs from it only infinitesimally. The derivative of a function y(x) is defined not as dy/dx but as the standard part of dy/dx.
For example, to find the derivative
f′(x) of the function
f(x) = x2, let dx be an infinitesimal. Then,
The use of the standard part in the definition of the derivative is a rigorous alternative to the traditional practice of neglecting the square of an infinitesimal quantity. After the third line of the differentiation above, the typical method from Newton through the 19th century would have been simply to discard the dx2 term. In the hyperreal system,
dx2 ≠ 0, since dx is nonzero, and the transfer principle can be applied to the statement that the square of any nonzero number is nonzero. However, the quantity dx2 is infinitesimally small compared to dx; that is, the hyperreal system contains a hierarchy of infinitesimal quantities.
lattice defined as a, a + dx, a + 2dx, ... a + ndx, where dx is infinitesimal, n is an infinite hypernatural, and the lower and upper bounds of integration are a and b = a + n dx.
containing the reals R as a subfield. Unlike the reals, the hyperreals do not form a standard metric space
, but by virtue of their order they carry an order topology
.
The use of the definite article the in the phrase the hyperreal numbers is somewhat misleading in that there is not a unique ordered field that is referred to in most treatments.
However, a 2003 paper by Kanovei and Shelah
shows that there is a definable, countably saturated
(meaning ω-saturated, but not of course countable) elementary extension
of the reals, which therefore has a good claim to the title of the hyperreal numbers. Furthermore, the field obtained by the ultrapower construction from the space of all real sequences, is unique up to isomorphism if one assumes the continuum hypothesis
.
The condition of being a hyperreal field is a stronger one than that of being a real closed field
strictly containing R. It is also stronger than that of being a superreal field in the sense of Dales and Woodin
.
, but the ultrafilter itself cannot be explicitly constructed. (Kanovei and Shelah have found a method that gives an explicit construction, at the cost of a significantly more complicated treatment.)
and (more explicitly) Leibniz
introduced differentials, they used infinitesimals and these were still regarded as useful by later mathematicians such as Euler
and Cauchy
. Nonetheless these concepts were from the beginning seen as suspect, notably by George Berkeley
. Berkeley's criticism centered on a perceived shift in hypothesis in the definition of the derivative in terms of infinitesimals (or fluxions), where dx is assumed to be nonzero at the beginning of the calculation, and to vanish at its conclusion (see Ghosts of departed quantities for details). When in the 1800s calculus
was put on a firm footing through the development of the (ε, δ)-definition of limit by Bolzano, Cauchy, Weierstrass
, and others, infinitesimals were largely abandoned, though research in non-Archimedean fields continued (Ehrlich 2006).
However, in the 1960s Abraham Robinson
showed how infinitely large and infinitesimal numbers can be rigorously defined and used to develop the field of non-standard analysis
. Robinson developed his theory nonconstructively, using model theory
; however it is possible to proceed using only algebra
and topology
, and proving the transfer principle as a consequence of the definitions. In other words hyperreal numbers per se, aside from their use in nonstandard analysis, have no necessary relationship to model theory or first order logic, although they were discovered by the application of model theoretic techniques from logic. Hyper-real fields were in fact originally introduced by Hewitt (1948) by purely algebraic techniques, using an ultrapower construction.
s of reals. In fact we can add and multiply sequences componentwise; for example:
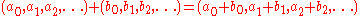
and analogously for multiplication.
This turns the set of such sequences into a commutative ring
, which is in fact a real algebra
A. We have a natural embedding of R in A by identifying the real number r with the sequence (r, r, r, ...) and this identification preserves the corresponding algebraic operations of the reals. The intuitive motivation is, for example, to represent an infinitesimal number using a sequence that approaches zero. The inverse of such a sequence would represent an infinite number. As we will see below, the difficulties arise because of the need to define rules for comparing such sequences in a manner that, although inevitably somewhat arbitrary, must be self-consistent and well defined. For example, we may have two sequences that differ in their first n members, but are equal after that; such sequences should clearly be considered as representing the same hyperreal number. Similarly, most sequences oscillate randomly forever, and we must find some way of taking such a sequence and interpreting it as, say, , where
, where  is a certain infinitesimal number.
is a certain infinitesimal number.
Comparing sequences is thus a delicate matter. We could, for example, try to define a relation between sequences in a componentwise fashion:
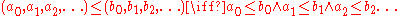
but here we run into trouble, since some entries of the first sequence may be bigger than the corresponding entries of the second sequence, and some others may be smaller. It follows that the relation defined in this way is only a partial order. To get around this, we have to specify which positions matter. Since there are infinitely many indices, we don't want finite sets of indices to matter. A consistent choice of index sets that matter is given by any free ultrafilter
U on the natural number
s; these can be characterized as ultrafilters which do not contain any finite sets. (The good news is that Zorn's lemma
guarantees the existence of many such U; the bad news is that they cannot be explicitly constructed.) We think of U as singling out those sets of indices that "matter": We write (a0, a1, a2, ...) ≤ (b0, b1, b2, ...) if and only if the set of natural numbers { n : an ≤ bn } is in U.
This is a total preorder and it turns into a total order
if we agree not to distinguish between two sequences a and b if a≤b and b≤a. With this identification, the ordered field *R of hyperreals is constructed. From an algebraic point of view, U allows us to define a corresponding maximal ideal
I in the commutative ring A (namely, the set of the sequences that vanish in some element of U), and then to define *R as A/I; as the quotient of a commutative ring by a maximal ideal, *R is a field. This is also notated A/U, directly in terms of the free ultrafilter U; the two are equivalent. The maximality of I follows from the possibility of, given a sequence a, construct a sequence b inverting its non-null elements and not altering its null entries. The product ab is in this case identified with the number 1, and any ideal containing 1 must be A. In the resulting field, these a and b are inverses.
The field A/U is an ultrapower
of R.
Since this field contains R it has cardinality at least the continuum. Since A has cardinality
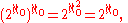
it is also no larger than , and hence has the same cardinality as R.
, and hence has the same cardinality as R.
One question we might ask is whether, if we had chosen a different free ultrafilter V, the quotient field A/U would be isomorphic as an ordered field to A/V. This question turns out to be equivalent to the continuum hypothesis
; in ZFC with the continuum hypothesis we can prove this field is unique up to order isomorphism
, and in ZFC with the negation of continuum hypothesis we can prove that there are non-order-isomorphic pairs of fields which are both countably indexed ultrapowers of the reals.
For more information about this method of construction, see ultraproduct
.
Let us see where these classes come from. Consider first the sequences of real numbers. They form a ring, that is, one can multiply add and subtract them, but not always divide by non-zero. The real numbers are considered as the constant sequences, the sequence is zero if it is identically zero, that is, an = 0 for all n.
In our ring of sequences one can get ab = 0 with neither a = 0 nor b = 0. Thus, if for two sequences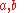 one has ab = 0, at least one of them should be declared zero. Surprisingly enough, there is a consistent way to do it. As a result, the classes of sequences that differ by some sequence declared zero will form a field which is called a hyperreal field
one has ab = 0, at least one of them should be declared zero. Surprisingly enough, there is a consistent way to do it. As a result, the classes of sequences that differ by some sequence declared zero will form a field which is called a hyperreal field
. It will contain the infinitesimals in addition to the ordinary real numbers, as well as infinitely large numbers (the reciprocals of infinitesimals, including those represented by sequences diverging to infinity). Also every hyperreal which is not infinitely large will be infinitely close to an ordinary real, in other words, it will be the sum of an ordinary real and an infinitesimal.
This construction is parallel to the construction of the reals from the rationals given by Cantor
. He started with the ring of the Cauchy sequence
s of rationals and declared all the sequences that converge to zero to be zero. The result is the reals. To continue the construction of hyperreals, let us consider the zero sets of our sequences, that is, the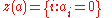 , that is,
, that is,  is the set of indexes
is the set of indexes  for which
for which  . It is clear that if
. It is clear that if  , then the union of
, then the union of  and
and 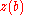 is N (the set of all natural numbers), so:
is N (the set of all natural numbers), so:
Now the idea is to single out a bunch U of subsets X of N and to declare that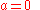 if and only if
if and only if  belongs to U. From the above conditions one can see that:
belongs to U. From the above conditions one can see that:
Any family of sets that satisfies (2)-(4) is called a filter
(an example: the complements to the finite sets, it is called the Fréchet filter
and it is used in the usual limit theory). If (1) also holds, U is called an ultrafilter
(because you can add no more sets to it without breaking it). The only explicitly known example of an ultrafilter is the family of sets containing a given element (in our case, say, the number 10). Such ultrafilters are called trivial, and if we use it in our construction, we come back to the ordinary real numbers. Any ultrafilter containing a finite set is trivial. It is known that any filter can be extended to an ultrafilter, but the proof uses the axiom of choice. The existence of a nontrivial ultrafilter (the ultrafilter lemma) can be added as an extra axiom, as it is weaker than the axiom of choice.
Now if we take a nontrivial ultrafilter (which is an extension of the Fréchet filter) and do our construction, we get the hyperreal numbers as a result.
If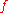 is a real function of a real variable
is a real function of a real variable  then
then 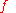 naturally extends to a hyperreal function of a hyperreal variable by composition:
naturally extends to a hyperreal function of a hyperreal variable by composition:
where means "the equivalence class of the sequence
means "the equivalence class of the sequence  relative to our ultrafilter", two sequences being in the same class if and only if the zero set of their difference belongs to our ultrafilter.
relative to our ultrafilter", two sequences being in the same class if and only if the zero set of their difference belongs to our ultrafilter.
All the arithmetical expressions and formulas make sense for hyperreals and hold true if they are true for the ordinary reals. One can prove that any finite (that is, such that for some ordinary real
for some ordinary real  ) hyperreal
) hyperreal  will be of the form
will be of the form  where
where 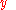 is an ordinary (called standard) real and
is an ordinary (called standard) real and 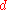 is an infinitesimal.
is an infinitesimal.
Now one can see that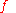 is continuous means that
is continuous means that 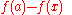 is infinitely small whenever
is infinitely small whenever  is, and
is, and 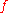 is differentiable means that
is differentiable means that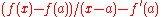
is infinitely small whenever is. Remarkably, if one allows
is. Remarkably, if one allows  to be hyperreal, the derivative will be automatically continuous (because,
to be hyperreal, the derivative will be automatically continuous (because, 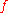 being differentiable at
being differentiable at  ,
,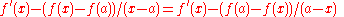
is infinitely small when is, therefore
is, therefore 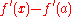 is also infinitely small when
is also infinitely small when  is).
is).
, and in fact a valuation ring
, with the unique maximal ideal S being the infinitesimals; the quotient F/S is isomorphic to the reals. Hence we have a homomorphic
mapping, st(x), from F to R whose kernel
consists of the infinitesimals and which sends every element x of F to a unique real number whose difference from x is in S; which is to say, is infinitesimal. Put another way, every finite nonstandard real number is "very close" to a unique real number, in the sense that if x is a finite nonstandard real, then there exists one and only one real number st(x) such that x – st(x) is infinitesimal. This number st(x) is called the standard part
of x, conceptually the same as x to the nearest real number. This operation is an order-preserving homomorphism and hence is well-behaved both algebraically and order theoretically. It is order-preserving though not isotonic, i.e. implies
implies 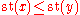 , but
, but  does not imply
does not imply  .
.
The map st is continuous with respect to the order topology on the finite hyperreals; in fact it is locally constant
.
, also called a T3.5 space, and C(X) is the algebra of continuous real-valued functions on X. Suppose M is a maximal ideal
in C(X). Then the factor algebra A = C(X)/M is a totally ordered field F containing the reals. If F strictly contains R then M is called a hyperreal ideal (terminology due to Hewitt
(1948)) and F a hyperreal field. Note that no assumption is being made that the cardinality of F is greater than R; it can in fact have the same cardinality.
An important special case is where the topology on X is the discrete topology
; in this case X can be identified with a cardinal number
κ and C(X) with the real algebra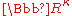 of functions from κ to R. The hyperreal fields we obtain in this case are called ultrapower
of functions from κ to R. The hyperreal fields we obtain in this case are called ultrapower
s of R and are identical to the ultrapowers constructed via free ultrafilter
s in model theory.
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
quantities. The hyperreals, or nonstandard reals, *R, are an extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R that contains numbers greater than anything of the form

Such a number is infinite, and its inverse is infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
. According to Keisler
Howard Jerome Keisler
H. Jerome Keisler is an American mathematician, currently professor emeritus at University of Wisconsin–Madison. His research has included model theory and non-standard analysis.His Ph.D...
(1994), the term "hyperreal" was introduced by Edwin Hewitt
Edwin Hewitt
Edwin Hewitt was an American mathematician known for his work in abstract harmonic analysis and for his discovery, in collaboration with Leonard Jimmie Savage, of the Hewitt–Savage zero-one law.He received his Ph.D...
(1948, p. 74), who spelled it with a hyphen: "hyper-real".
The hyperreal numbers satisfy the transfer principle
Transfer principle
In model theory, a transfer principle states that all statements of some language that are true for some structure are true for another structure...
, which is a mathematical implementation of Leibniz's heuristic Law of Continuity
Law of Continuity
The Law of Continuity is a heuristic principle introduced by Leibniz based on earlier work by Nicholas of Cusa and Johannes Kepler. It is the principle that "whatever succeeds for the finite, also succeeds for the infinite"...
. The transfer principle states that true first order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
statements about R are also valid in *R. For example, the commutative law of addition, x + y = y + x, holds for the hyperreals just as it does for the reals; since R is a real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
, so is *R. Since sin πn = 0 for all integers n, one also has sin πH = 0 for all hyperinteger
Hyperinteger
In non-standard analysis, a hyperinteger N is a hyperreal number equal to its own integer part. A hyperinteger may be either finite or infinite. A finite hyperinteger is an ordinary integer...
s H. The transfer principle for ultrapowers is a consequence of Łoś' theorem of 1955.
Concerns about the logical soundness
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
of arguments involving infinitesimals date back to ancient Greek mathematics, with Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
replacing such proofs with ones using other techniques such as the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
. In the 1960s Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
proved that the hyperreals were logically consistent if and only if the reals were. This put to rest the fear that any proof involving infinitesimals might be unsound, provided that they were manipulated according to the logical rules which Robinson delineated.
The application of hyperreal numbers and in particular the transfer principle to problems of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
is called non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
; some find it more intuitive than standard real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
. One immediate application is the definition of the basic concepts of analysis such as derivative and integral in a direct fashion, without passing via logical complications of multiple quantifiers. Thus, the derivative of f(x) becomes
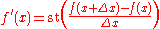 for an infinitesimal
for an infinitesimal 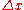 , where st(·) denotes the standard part function
, where st(·) denotes the standard part functionStandard part function
In non-standard analysis, the standard part function is a function from the limited hyperreals to the reals, which associates to every hyperreal, the unique real infinitely close to it. As such, it is a mathematical implementation of the historical concept of adequality introduced by Pierre de...
, which associates to every finite hyperreal, the unique real infinitely close to it.
The transfer principle
The idea of the hyperreal system is to extend the real numbers R to form a system *R that includes infinitesimal and infinite numbers, but without changing any of the elementary axioms of algebra. Any statement of the form "for any number x..." that is true for the reals is also true for the hyperreals. For example, the axiom that states "for any number x, x + 0 = x" still applies. The same is true for quantification over several numbers, e.g., "for any numbers x and y, xy = yx." This ability to carry over statements from the reals to the hyperreals is called the transfer principleTransfer principle
In model theory, a transfer principle states that all statements of some language that are true for some structure are true for another structure...
. However, statements of the form "for any set of numbers S ..." may not carry over. The only properties that differ between the reals and the hyperreals are those that rely on quantification over sets, or other higher-level structures such as functions and relations, which are typically constructed out of sets. Each real set, function, and relation has its natural hyperreal extension, satisfying the same first-order properties. The kinds of logical sentences that obey this restriction on quantification are referred to as statements in first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
.
The transfer principle, however, doesn't mean that R and *R have identical behavior. For instance, in *R there exists an element ω such that
but there is no such number in R. This is possible because the existence of such a number cannot be expressed as a first order statement.
Calculus with algebraic functions
Informal notations for non-real quantities have historically appeared in calculus in two contexts: as infinitesimals like dx and as the symbol ∞, used, for example, in limits of integration of improper integrals.As an example of the transfer principle, the statement that for any nonzero number x, 2x ≠ x, is true for the real numbers, and it is in the form required by the transfer principle, so it is also true for the hyperreal numbers. This shows that it is not possible to use a generic symbol such as ∞ for all the infinite quantities in the hyperreal system; infinite quantities differ in magnitude from other infinite quantities, and infinitesimals from other infinitesimals.
Similarly, the casual use of 1/0 = ∞ is invalid, since the transfer principle applies to the statement that division by zero is undefined. The rigorous counterpart of such a calculation would be that if ε is infinitesimal, then 1/ε is infinite.
For any finite hyperreal number x, its standard part, st x, is defined as the unique real number that differs from it only infinitesimally. The derivative of a function y(x) is defined not as dy/dx but as the standard part of dy/dx.
For example, to find the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
f′(x) of the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f(x) = x2, let dx be an infinitesimal. Then,
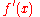 |
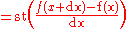 |
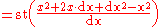 |
|
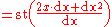 |
|
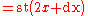 |
|
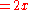 |
The use of the standard part in the definition of the derivative is a rigorous alternative to the traditional practice of neglecting the square of an infinitesimal quantity. After the third line of the differentiation above, the typical method from Newton through the 19th century would have been simply to discard the dx2 term. In the hyperreal system,
dx2 ≠ 0, since dx is nonzero, and the transfer principle can be applied to the statement that the square of any nonzero number is nonzero. However, the quantity dx2 is infinitesimally small compared to dx; that is, the hyperreal system contains a hierarchy of infinitesimal quantities.
Integration
One way of defining a definite integral in the hyperreal system is as the standard part of an infinite sum on a hyperfiniteHyperfinite
Hyperfinite may refer to:*Hyperfinite set*von Neumann algebra...
lattice defined as a, a + dx, a + 2dx, ... a + ndx, where dx is infinitesimal, n is an infinite hypernatural, and the lower and upper bounds of integration are a and b = a + n dx.
Properties
The hyperreals *R form an ordered fieldOrdered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
containing the reals R as a subfield. Unlike the reals, the hyperreals do not form a standard metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, but by virtue of their order they carry an order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
.
The use of the definite article the in the phrase the hyperreal numbers is somewhat misleading in that there is not a unique ordered field that is referred to in most treatments.
However, a 2003 paper by Kanovei and Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
shows that there is a definable, countably saturated
Saturated model
In mathematical logic, and particularly in its subfield model theory, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size...
(meaning ω-saturated, but not of course countable) elementary extension
Elementary substructure
In model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
of the reals, which therefore has a good claim to the title of the hyperreal numbers. Furthermore, the field obtained by the ultrapower construction from the space of all real sequences, is unique up to isomorphism if one assumes the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
.
The condition of being a hyperreal field is a stronger one than that of being a real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
strictly containing R. It is also stronger than that of being a superreal field in the sense of Dales and Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
.
Development
The hyperreals can be developed either axiomatically or by more constructively oriented methods. The essence of the axiomatic approach is to assert (1) the existence of at least one infinitesimal number, and (2) the validity of the transfer principle. In the following subsection we give a detailed outline of a more constructive approach. This method allows one to construct the hyperreals if given a set-theoretic object called an ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
, but the ultrafilter itself cannot be explicitly constructed. (Kanovei and Shelah have found a method that gives an explicit construction, at the cost of a significantly more complicated treatment.)
From Newton to Robinson
When NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and (more explicitly) Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
introduced differentials, they used infinitesimals and these were still regarded as useful by later mathematicians such as Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
and Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
. Nonetheless these concepts were from the beginning seen as suspect, notably by George Berkeley
George Berkeley
George Berkeley , also known as Bishop Berkeley , was an Irish philosopher whose primary achievement was the advancement of a theory he called "immaterialism"...
. Berkeley's criticism centered on a perceived shift in hypothesis in the definition of the derivative in terms of infinitesimals (or fluxions), where dx is assumed to be nonzero at the beginning of the calculation, and to vanish at its conclusion (see Ghosts of departed quantities for details). When in the 1800s calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
was put on a firm footing through the development of the (ε, δ)-definition of limit by Bolzano, Cauchy, Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, and others, infinitesimals were largely abandoned, though research in non-Archimedean fields continued (Ehrlich 2006).
However, in the 1960s Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
showed how infinitely large and infinitesimal numbers can be rigorously defined and used to develop the field of non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
. Robinson developed his theory nonconstructively, using model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
; however it is possible to proceed using only algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and proving the transfer principle as a consequence of the definitions. In other words hyperreal numbers per se, aside from their use in nonstandard analysis, have no necessary relationship to model theory or first order logic, although they were discovered by the application of model theoretic techniques from logic. Hyper-real fields were in fact originally introduced by Hewitt (1948) by purely algebraic techniques, using an ultrapower construction.
The ultrapower construction
We are going to construct a hyperreal field via sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of reals. In fact we can add and multiply sequences componentwise; for example:
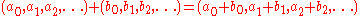
and analogously for multiplication.
This turns the set of such sequences into a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, which is in fact a real algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
A. We have a natural embedding of R in A by identifying the real number r with the sequence (r, r, r, ...) and this identification preserves the corresponding algebraic operations of the reals. The intuitive motivation is, for example, to represent an infinitesimal number using a sequence that approaches zero. The inverse of such a sequence would represent an infinite number. As we will see below, the difficulties arise because of the need to define rules for comparing such sequences in a manner that, although inevitably somewhat arbitrary, must be self-consistent and well defined. For example, we may have two sequences that differ in their first n members, but are equal after that; such sequences should clearly be considered as representing the same hyperreal number. Similarly, most sequences oscillate randomly forever, and we must find some way of taking such a sequence and interpreting it as, say,
 , where
, where  is a certain infinitesimal number.
is a certain infinitesimal number.Comparing sequences is thus a delicate matter. We could, for example, try to define a relation between sequences in a componentwise fashion:
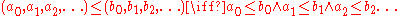
but here we run into trouble, since some entries of the first sequence may be bigger than the corresponding entries of the second sequence, and some others may be smaller. It follows that the relation defined in this way is only a partial order. To get around this, we have to specify which positions matter. Since there are infinitely many indices, we don't want finite sets of indices to matter. A consistent choice of index sets that matter is given by any free ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
U on the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s; these can be characterized as ultrafilters which do not contain any finite sets. (The good news is that Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
guarantees the existence of many such U; the bad news is that they cannot be explicitly constructed.) We think of U as singling out those sets of indices that "matter": We write (a0, a1, a2, ...) ≤ (b0, b1, b2, ...) if and only if the set of natural numbers { n : an ≤ bn } is in U.
This is a total preorder and it turns into a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
if we agree not to distinguish between two sequences a and b if a≤b and b≤a. With this identification, the ordered field *R of hyperreals is constructed. From an algebraic point of view, U allows us to define a corresponding maximal ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I in the commutative ring A (namely, the set of the sequences that vanish in some element of U), and then to define *R as A/I; as the quotient of a commutative ring by a maximal ideal, *R is a field. This is also notated A/U, directly in terms of the free ultrafilter U; the two are equivalent. The maximality of I follows from the possibility of, given a sequence a, construct a sequence b inverting its non-null elements and not altering its null entries. The product ab is in this case identified with the number 1, and any ideal containing 1 must be A. In the resulting field, these a and b are inverses.
The field A/U is an ultrapower
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
of R.
Since this field contains R it has cardinality at least the continuum. Since A has cardinality
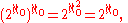
it is also no larger than
 , and hence has the same cardinality as R.
, and hence has the same cardinality as R.One question we might ask is whether, if we had chosen a different free ultrafilter V, the quotient field A/U would be isomorphic as an ordered field to A/V. This question turns out to be equivalent to the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
; in ZFC with the continuum hypothesis we can prove this field is unique up to order isomorphism
Order isomorphism
In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...
, and in ZFC with the negation of continuum hypothesis we can prove that there are non-order-isomorphic pairs of fields which are both countably indexed ultrapowers of the reals.
For more information about this method of construction, see ultraproduct
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
.
An intuitive approach to the ultrapower construction
The following is an intuitive way of understanding the hyperreal numbers. The approach taken here is very close to the one in the book by Goldblatt. Recall that the sequences converging to zero are sometimes called infinitely small. These are almost the infinitesimals in a sense; the true infinitesimals include the classes of sequences that contain a sequence converging to zero. However, there may be infinitesimals not represented by null sequences; see P-point.Let us see where these classes come from. Consider first the sequences of real numbers. They form a ring, that is, one can multiply add and subtract them, but not always divide by non-zero. The real numbers are considered as the constant sequences, the sequence is zero if it is identically zero, that is, an = 0 for all n.
In our ring of sequences one can get ab = 0 with neither a = 0 nor b = 0. Thus, if for two sequences
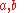 one has ab = 0, at least one of them should be declared zero. Surprisingly enough, there is a consistent way to do it. As a result, the classes of sequences that differ by some sequence declared zero will form a field which is called a hyperreal field
one has ab = 0, at least one of them should be declared zero. Surprisingly enough, there is a consistent way to do it. As a result, the classes of sequences that differ by some sequence declared zero will form a field which is called a hyperreal fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. It will contain the infinitesimals in addition to the ordinary real numbers, as well as infinitely large numbers (the reciprocals of infinitesimals, including those represented by sequences diverging to infinity). Also every hyperreal which is not infinitely large will be infinitely close to an ordinary real, in other words, it will be the sum of an ordinary real and an infinitesimal.
This construction is parallel to the construction of the reals from the rationals given by Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
. He started with the ring of the Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s of rationals and declared all the sequences that converge to zero to be zero. The result is the reals. To continue the construction of hyperreals, let us consider the zero sets of our sequences, that is, the
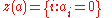 , that is,
, that is,  is the set of indexes
is the set of indexes  for which
for which  . It is clear that if
. It is clear that if  , then the union of
, then the union of  and
and 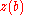 is N (the set of all natural numbers), so:
is N (the set of all natural numbers), so:
- One of the sequences that vanish on 2 complementary sets should be declared zero
- If
 is declared zero,
is declared zero, 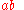 should be declared zero too, no matter what
should be declared zero too, no matter what  is.
is. - If both
 and
and  are declared zero, then
are declared zero, then  should also be declared zero.
should also be declared zero.
Now the idea is to single out a bunch U of subsets X of N and to declare that
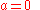 if and only if
if and only if  belongs to U. From the above conditions one can see that:
belongs to U. From the above conditions one can see that:
- From 2 complementary sets one belongs to U
- Any set containing a set that belongs to U, also belongs to U.
- An intersection of any 2 sets belonging to U belongs to U.
- Finally, we do not want an empty set to belong to U because then everything becomes zero, as every set contains an empty set.
Any family of sets that satisfies (2)-(4) is called a filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
(an example: the complements to the finite sets, it is called the Fréchet filter
Fréchet filter
In mathematics, Fréchet filter is an important concept in order theory.If X is an infinite set, the Fréchet filter,also called cofinite filter on X, is the set of all subsets of X having finite complement in X....
and it is used in the usual limit theory). If (1) also holds, U is called an ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
(because you can add no more sets to it without breaking it). The only explicitly known example of an ultrafilter is the family of sets containing a given element (in our case, say, the number 10). Such ultrafilters are called trivial, and if we use it in our construction, we come back to the ordinary real numbers. Any ultrafilter containing a finite set is trivial. It is known that any filter can be extended to an ultrafilter, but the proof uses the axiom of choice. The existence of a nontrivial ultrafilter (the ultrafilter lemma) can be added as an extra axiom, as it is weaker than the axiom of choice.
Now if we take a nontrivial ultrafilter (which is an extension of the Fréchet filter) and do our construction, we get the hyperreal numbers as a result.
If
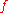 is a real function of a real variable
is a real function of a real variable  then
then 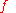 naturally extends to a hyperreal function of a hyperreal variable by composition:
naturally extends to a hyperreal function of a hyperreal variable by composition:
where
 means "the equivalence class of the sequence
means "the equivalence class of the sequence  relative to our ultrafilter", two sequences being in the same class if and only if the zero set of their difference belongs to our ultrafilter.
relative to our ultrafilter", two sequences being in the same class if and only if the zero set of their difference belongs to our ultrafilter.All the arithmetical expressions and formulas make sense for hyperreals and hold true if they are true for the ordinary reals. One can prove that any finite (that is, such that
 for some ordinary real
for some ordinary real  ) hyperreal
) hyperreal  will be of the form
will be of the form  where
where 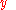 is an ordinary (called standard) real and
is an ordinary (called standard) real and 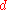 is an infinitesimal.
is an infinitesimal.Now one can see that
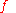 is continuous means that
is continuous means that 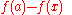 is infinitely small whenever
is infinitely small whenever  is, and
is, and 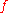 is differentiable means that
is differentiable means that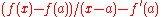
is infinitely small whenever
 is. Remarkably, if one allows
is. Remarkably, if one allows  to be hyperreal, the derivative will be automatically continuous (because,
to be hyperreal, the derivative will be automatically continuous (because, 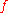 being differentiable at
being differentiable at  ,
,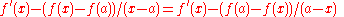
is infinitely small when
 is, therefore
is, therefore 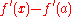 is also infinitely small when
is also infinitely small when  is).
is).Properties of infinitesimal and infinite numbers
The finite elements F of *R form a local ringLocal ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
, and in fact a valuation ring
Valuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
, with the unique maximal ideal S being the infinitesimals; the quotient F/S is isomorphic to the reals. Hence we have a homomorphic
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
mapping, st(x), from F to R whose kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
consists of the infinitesimals and which sends every element x of F to a unique real number whose difference from x is in S; which is to say, is infinitesimal. Put another way, every finite nonstandard real number is "very close" to a unique real number, in the sense that if x is a finite nonstandard real, then there exists one and only one real number st(x) such that x – st(x) is infinitesimal. This number st(x) is called the standard part
Standard part function
In non-standard analysis, the standard part function is a function from the limited hyperreals to the reals, which associates to every hyperreal, the unique real infinitely close to it. As such, it is a mathematical implementation of the historical concept of adequality introduced by Pierre de...
of x, conceptually the same as x to the nearest real number. This operation is an order-preserving homomorphism and hence is well-behaved both algebraically and order theoretically. It is order-preserving though not isotonic, i.e.
 implies
implies 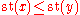 , but
, but  does not imply
does not imply  .
.- We have, if both x and y are finite,
-

-

- If x is finite and not infinitesimal.
-
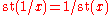
- x is real if and only if
-
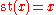
The map st is continuous with respect to the order topology on the finite hyperreals; in fact it is locally constant
Locally constant function
In mathematics, a function f from a topological space A to a set B is called locally constant, if for every a in A there exists a neighborhood U of a, such that f is constant on U....
.
Hyperreal fields
Suppose X is a Tychonoff spaceTychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
, also called a T3.5 space, and C(X) is the algebra of continuous real-valued functions on X. Suppose M is a maximal ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
in C(X). Then the factor algebra A = C(X)/M is a totally ordered field F containing the reals. If F strictly contains R then M is called a hyperreal ideal (terminology due to Hewitt
Hewitt
- People :In science:* Carl Hewitt, US scientist* Edwin Hewitt, mathematician* John Hewitt , British and South African herpetologist and museum curator* Paul G...
(1948)) and F a hyperreal field. Note that no assumption is being made that the cardinality of F is greater than R; it can in fact have the same cardinality.
An important special case is where the topology on X is the discrete topology
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
; in this case X can be identified with a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ and C(X) with the real algebra
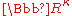 of functions from κ to R. The hyperreal fields we obtain in this case are called ultrapower
of functions from κ to R. The hyperreal fields we obtain in this case are called ultrapowerUltraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
s of R and are identical to the ultrapowers constructed via free ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s in model theory.
See also
- HyperintegerHyperintegerIn non-standard analysis, a hyperinteger N is a hyperreal number equal to its own integer part. A hyperinteger may be either finite or infinite. A finite hyperinteger is an ordinary integer...
- Real closed fieldReal closed fieldIn mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s - Non-standard calculusNon-standard calculusIn mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...
- Constructive non-standard analysisConstructive non-standard analysisIn mathematics, constructive nonstandard analysis is a version of Abraham Robinson's non-standard analysis, developed by Moerdijk , Palmgren , Ruokolainen . Ruokolainen wrote:-References:...
Further reading
- Hatcher, William S. (1982) "Calculus is Algebra", American Mathematical MonthlyAmerican Mathematical MonthlyThe American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
89: 362–370. - Hewitt, Edwin (1948) Rings of real-valued continuous functions. I. Trans. Amer. Math. Soc. 64, 45—99.
- Keisler, H. Jerome (1994) The hyperreal line. Real numbers, generalizations of the reals, and theories of continua, 207—237, Synthese Lib., 242, Kluwer Acad. Publ., Dordrecht.
External links
- Crowell, Calculus. A text using infinitesimals.
- Hermoso, Nonstandard Analysis and the Hyperreals. A gentle introduction.
- Keisler, Elementary Calculus: An Approach Using Infinitesimals. Includes an axiomatic treatment of the hyperreals, and is freely available under a Creative Commons license
- Stroyan, A Brief Introduction to Infinitesimal Calculus


