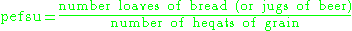Moscow Mathematical Papyrus
Encyclopedia
The Moscow Mathematical Papyrus is an ancient Egyptian mathematical
papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev
. Golenishchev bought the papyrus in 1892 or 1893 in Thebes
. It later entered the collection of the Pushkin State Museum of Fine Arts in Moscow, where it remains today.
Based on the palaeography
and orthography of the hieratic
text, the text was most likely written down in the 13th dynasty
and based on older material probably dating to the Twelfth dynasty of Egypt
, roughly 1850 BC. Approximately 18 feet long and varying between 1½ and 3 inches wide, its format was divided into 25 problems with solutions by the Soviet
Orientalist
Vasily Vasilievich Struve
in 1930. It is a well-known mathematical papyrus along with the Rhind Mathematical Papyrus
. The Moscow Mathematical Papyrus is older than the Rhind Mathematical Papyrus, while the latter is the larger of the two.
. The papyrus is well known for some of its geometry problems. Problems 10 and 14 compute a surface area and the volume of a frustum
respectively. The remaining problems are more common in nature.
also contains four of these type of problems. Problems 1, 19, and 25 of the Moscow Papyrus are Aha problems. For instance problem 19 asks one to calculate a quantity taken 1 and ½ times and added to 4 to make 10. In other words, in modern mathematical notation one is asked to solve
A higher pefsu number means weaker bread or beer. The pefsu number is mentioned in many offering lists. For example problem 8 translates as:
(Struve, Gillings) or possibly the area of a semi-cylinder (Peet). Below we assume that the problem refers to the area of a hemisphere.
The text of problem 10 runs like this: "Example of calculating a basket. You are given a basket with a mouth of 4 1/2 . What is its surface? Take 1/9 of 9 (since) the basket is half an egg-shell. You get 1. Calculate the remainder which is 8. Calculate 1/9 of 8. You get 2/3 + 1/6 + 1/18. Find the remainder of this 8 after subtracting 2/3 + 1/6 + 1/18. You get 7 + 1/9. Multiply 7 + 1/9 by 4 + 1/2. You get 32. Behold this is its area. You have found it correctly."
The solution amounts to computing the area as
This means the scribe of the Moscow Papyrus used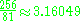
to approximate pi.
The 14th problem of the Moscow Mathematical calculates the volume of a frustum
.
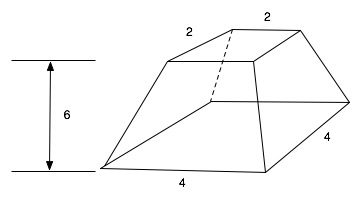
Problem 14 states that a pyramid has been truncated in such a way that the top area is a square of length 2 units, the bottom a square of length 4 units, and the height 6 units, as shown. The volume is found to be 56 cubic units, which is correct.
The text of the example runs like this: "If you are told: a truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top: You are to square the 4; result 16. You are to double 4; result 8. You are to square this 2; result 4. You are to add the 16 and the 8 and the 4; result 28. You are to take 1/3 of 6; result 2. You are to take 28 twice; result 56. See, it is of 56. You will find (it) right"
The solution to the problem indicates that the Egyptians knew the correct formula for obtaining the volume
of a truncated pyramid
:
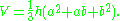
We do not know how the Egyptians arrived at the formula for the volume of a frustum
.
General papyri:
For the 2/n tables see:
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev
Vladimir Golenishchev
Vladimir Semyonovich Golenishchev was one of the first and most accomplished Russian Egyptologists.Golenishchev came from an old noble family, of which Field Marshal Kutuzov was also a member, and was educated at the Saint Petersburg University. In 1884–85 he organized and financed excavations in...
. Golenishchev bought the papyrus in 1892 or 1893 in Thebes
Thebes, Egypt
Thebes is the Greek name for a city in Ancient Egypt located about 800 km south of the Mediterranean, on the east bank of the river Nile within the modern city of Luxor. The Theban Necropolis is situated nearby on the west bank of the Nile.-History:...
. It later entered the collection of the Pushkin State Museum of Fine Arts in Moscow, where it remains today.
Based on the palaeography
Palaeography
Palaeography, also spelt paleography is the study of ancient writing. Included in the discipline is the practice of deciphering, reading, and dating historical manuscripts, and the cultural context of writing, including the methods with which writing and books were produced, and the history of...
and orthography of the hieratic
Hieratic
Hieratic refers to a cursive writing system that was used in the provenance of the pharaohs in Egypt and Nubia that developed alongside the hieroglyphic system, to which it is intimately related...
text, the text was most likely written down in the 13th dynasty
Thirteenth dynasty of Egypt
The thirteenth dynasty of ancient Egypt is often combined with Dynasties XI, XII and XIV under the group title Middle Kingdom. Other writers separate it from these dynasties and join it to Dynasties XIV through XVII as part of the Second Intermediate Period...
and based on older material probably dating to the Twelfth dynasty of Egypt
Twelfth dynasty of Egypt
The twelfth dynasty of ancient Egypt is often combined with Dynasties XI, XIII and XIV under the group title Middle Kingdom.-Rulers:Known rulers of the twelfth dynasty are as follows :...
, roughly 1850 BC. Approximately 18 feet long and varying between 1½ and 3 inches wide, its format was divided into 25 problems with solutions by the Soviet
Soviet Union
The Soviet Union , officially the Union of Soviet Socialist Republics , was a constitutionally socialist state that existed in Eurasia between 1922 and 1991....
Orientalist
Oriental studies
Oriental studies is the academic field of study that embraces Near Eastern and Far Eastern societies and cultures, languages, peoples, history and archaeology; in recent years the subject has often been turned into the newer terms of Asian studies and Middle Eastern studies...
Vasily Vasilievich Struve
Vasily Vasilievich Struve
Vasily Vasilievich Struve was a Soviet orientalist from the Struve family, the founder of the Soviet scientific school of researchers on Ancient Near East history....
in 1930. It is a well-known mathematical papyrus along with the Rhind Mathematical Papyrus
Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
. The Moscow Mathematical Papyrus is older than the Rhind Mathematical Papyrus, while the latter is the larger of the two.
Exercises contained in the Moscow Papyrus
The problems in the Moscow Papyrus follow no particular order, and the solutions of the problems provide much less detail than those in the Rhind Mathematical PapyrusRhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
. The papyrus is well known for some of its geometry problems. Problems 10 and 14 compute a surface area and the volume of a frustum
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
respectively. The remaining problems are more common in nature.
Ship’s part problems
Problems 2 and 3 are ship’s part problems. One of the problems calculates the length of a ship’s rudder and the other computes the length of a ship’s mast given that it is 1/3 + 1/5 of the length of a cedar log originally 30 cubits long.Aha problems
Aha problems involve finding unknown quantities (referred to as Aha) if the sum of the quantity and part(s) of it are given. The Rhind Mathematical PapyrusRhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
also contains four of these type of problems. Problems 1, 19, and 25 of the Moscow Papyrus are Aha problems. For instance problem 19 asks one to calculate a quantity taken 1 and ½ times and added to 4 to make 10. In other words, in modern mathematical notation one is asked to solve
Pefsu problems
Most of the problems are pefsu problems: 10 of the 25 problems. A pefsu measures the strength of the beer made from a heqat of grain
A higher pefsu number means weaker bread or beer. The pefsu number is mentioned in many offering lists. For example problem 8 translates as:
- (1) Example of calculating 100 loaves of bread of pefsu 20
- (2) If someone says to you: “You have 100 loaves of bread of pefsu 20
- (3) to be exchanged for beer of pefsu 4
- (4) like 1/2 1/4 malt-date beer
- (5) First calculate the grain required for the 100 loaves of the bread of pefsu 20
- (6) The result is 5 heqat. Then reckon what you need for a des-jug of beer like the beer called 1/2 1/4 malt-date beer
- (7) The result is 1/2 of the heqat measure needed for des-jug of beer made from Upper-Egyptian grain.
- (8) Calculate 1/2 of 5 heqat, the result will be 2 1/2
- (9) Take this 2 1/2 four times
- (10) The result is 10. Then you say to him:
- (11) Behold! The beer quantity is found to be correct.
Baku problems
Problems 11 and 23 are Baku problems. These calculate the output of workers. Problem 11 asks if someone brings in 100 logs measuring 5 by 5, then how many logs measuring 4 by 4 does this correspond to? Problem 23 finds the output of a shoemaker given that he has to cut and decorate sandals.Geometry problems
Seven of the twenty-five problems are geometry problems and range from computing areas of triangles, to finding the surface area of a hemisphere (problem 10) and finding the volume of a frustum (a truncated pyramid).Problem 10
The 10th problem of the Moscow Mathematical Papyrus asks for a calculation of the surface area of a hemisphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(Struve, Gillings) or possibly the area of a semi-cylinder (Peet). Below we assume that the problem refers to the area of a hemisphere.
The text of problem 10 runs like this: "Example of calculating a basket. You are given a basket with a mouth of 4 1/2 . What is its surface? Take 1/9 of 9 (since) the basket is half an egg-shell. You get 1. Calculate the remainder which is 8. Calculate 1/9 of 8. You get 2/3 + 1/6 + 1/18. Find the remainder of this 8 after subtracting 2/3 + 1/6 + 1/18. You get 7 + 1/9. Multiply 7 + 1/9 by 4 + 1/2. You get 32. Behold this is its area. You have found it correctly."
The solution amounts to computing the area as
This means the scribe of the Moscow Papyrus used
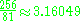to approximate pi.Problem 14: Volume of frustum of square pyramid
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
.
Problem 14 states that a pyramid has been truncated in such a way that the top area is a square of length 2 units, the bottom a square of length 4 units, and the height 6 units, as shown. The volume is found to be 56 cubic units, which is correct.
The text of the example runs like this: "If you are told: a truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top: You are to square the 4; result 16. You are to double 4; result 8. You are to square this 2; result 4. You are to add the 16 and the 8 and the 4; result 28. You are to take 1/3 of 6; result 2. You are to take 28 twice; result 56. See, it is of 56. You will find (it) right"
The solution to the problem indicates that the Egyptians knew the correct formula for obtaining the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a truncated pyramid
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
:
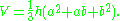
We do not know how the Egyptians arrived at the formula for the volume of a frustum
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
.
Other papyri
Other mathematical texts from Ancient Egypt include:- Berlin PapyrusBerlin papyrusThe Berlin Papyrus 6619, commonly known as the Berlin Papyrus, is an ancient Egyptian papyrus document from the Middle Kingdom. This papyrus was found at the ancient burial ground of Saqqara in the early 19th century CE....
also known as Berlin Papyrus 6619 - Egyptian Mathematical Leather RollEgyptian Mathematical Leather RollThe Egyptian Mathematical Leather Roll was a 10 × 17 in leather roll purchased by Alexander Henry Rhind in 1858...
- Lahun Mathematical PapyriLahun Mathematical PapyriThe Lahun Mathematical Papyri are part of a collection of Kahun Papyri discovered at El-Lahun by Flinders Petrie during excavations of a worker's town near the pyramid of Sesostris II...
- Rhind Mathematical PapyrusRhind Mathematical PapyrusThe Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
General papyri:
- Papyrus Harris IPapyrus Harris IPapyrus Harris I is also known as the Great Harris Papyrus and simply the Harris Papyrus . Its technical designation is Papyrus British Museum 9999...
- Rollin Papyrus
For the 2/n tables see:
- RMP 2/n table
Full Text of the Moscow Mathematical Papyrus
- Struve, Vasilij Vasil'evič, and Boris Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau. Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
Other references
- Allen, Don. April 2001. The Moscow Papyrus and Summary of Egyptian Mathematics.
- Couchoud, Sylvia, http://translate.google.com/translate?hl=en&sl=fr&u=http://fr.wikipedia.org/wiki/Sylvia_Couchoud&sa=X&oi=translate&resnum=10&ct=result&prev=/search%3Fq%3Dcouchoud,%2Bsylvia%26hl%3Den%26rlz%3D1B2GGFB_enUS216US216.
- Gardner, Milo, http://planetmath.org/encyclopedia/MoscowMathematicalPapyrus.html.
- Imhausen, A., Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Wiesbaden 2003.
- Mathpages.com. The Prismoidal Formula.
- O'Connor and Robertson, 2000. Mathematics in Egyptian Papyri.
- Truman State University, Math and Computer Science Division. Mathematics and the Liberal Arts: Ancient Egypt and The Moscow Mathematical Papyrus.
- Williams, Scott W. Mathematicians of the African Diaspora, containing a page on Egyptian Mathematics Papyri.
- Zahrt, Kim R. W. Thoughts on Ancient Egyptian Mathematics.