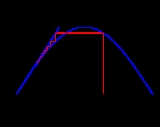
Fixed point iteration
Encyclopedia
In numerical analysis
, fixed-point iteration is a method of computing fixed points
of iterated function
s.
More specifically, given a function defined on the real number
defined on the real number
s with real values and given a point in the domain
in the domain
of , the fixed point iteration
, the fixed point iteration
is

which gives rise to the sequence
 which is hoped to converge
which is hoped to converge
to a point . If
. If  is continuous, then one can prove that the obtained
is continuous, then one can prove that the obtained  is a fixed point of
is a fixed point of  , i.e.,
, i.e.,
 .
.
More generally, the function f can be defined on any metric space
with values in that same space.
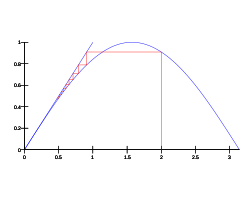
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, fixed-point iteration is a method of computing fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
s.
More specifically, given a function
 defined on the real number
defined on the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with real values and given a point
 in the domain
in the domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of
 , the fixed point iteration
, the fixed point iterationIteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
is

which gives rise to the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
 which is hoped to converge
which is hoped to convergeLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
to a point
 . If
. If  is continuous, then one can prove that the obtained
is continuous, then one can prove that the obtained  is a fixed point of
is a fixed point of  , i.e.,
, i.e., .
.More generally, the function f can be defined on any metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
with values in that same space.
Examples
- A first simple and useful example is the Babylonian method for computing the square rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of a>0, which consists in taking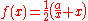 , i.e. the mean value of x and a/x, to approach the limit
, i.e. the mean value of x and a/x, to approach the limit  (from whatever starting point
(from whatever starting point  ). This is a special case of Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
). This is a special case of Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
quoted below.

- The fixed-point iteration
 converges to the unique fixed point of the function
converges to the unique fixed point of the function  for any starting point
for any starting point  This example does satisfy the hypotheses of the Banach fixed point theoremBanach fixed point theoremIn mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
This example does satisfy the hypotheses of the Banach fixed point theoremBanach fixed point theoremIn mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
. Hence, the error after n steps satisfies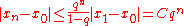 (where we can take
(where we can take  , if we start from
, if we start from  .) When the error is less than a multiple of
.) When the error is less than a multiple of 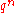 for some constant q, we say that we have linear convergence. The Banach fixed-point theorem allows one to obtain fixed-point iterations with linear convergence.
for some constant q, we say that we have linear convergence. The Banach fixed-point theorem allows one to obtain fixed-point iterations with linear convergence.
- The fixed-point iteration
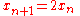 will diverge unless
will diverge unless  . We say that the fixed point of
. We say that the fixed point of 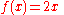 is repelling.
is repelling.
- The requirement that f is continuous is important, as the following example shows. The iteration

converges to 0 for all values of .
.
However, 0 is not a fixed point of the function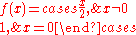
as this function is not continuous at , and in fact has no fixed points.
, and in fact has no fixed points.
Applications
- Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
for a given differentiable function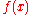 is
is 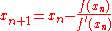 . If we write
. If we write 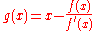 we may rewrite the Newton iteration as the fixed point iteration
we may rewrite the Newton iteration as the fixed point iteration 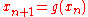 . If this iteration converges to a fixed point
. If this iteration converges to a fixed point  of
of 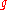 then
then 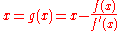 so
so 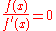 . The inverse of anything is nonzero, therefore
. The inverse of anything is nonzero, therefore 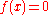 : x is a root of f. Under the assumptions of the Banach fixed point theoremBanach fixed point theoremIn mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
: x is a root of f. Under the assumptions of the Banach fixed point theoremBanach fixed point theoremIn mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
, the Newton iteration, framed as the fixed point method, demonstrates linear convergence. However, a more detailed analysis shows quadratic convergence, i.e.,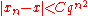 , under certain circumstances.
, under certain circumstances.
- Halley's methodHalley's methodIn numerical analysis, Halley’s method is a root-finding algorithm used for functions of one real variable with a continuous second derivative, i.e., C2 functions. It is named after its inventor Edmond Halley, who also discovered Halley's Comet....
is similar to Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
but, when it works correctly, its error is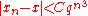 (cubic convergence). In general, it is possible to design methods that converge with speed
(cubic convergence). In general, it is possible to design methods that converge with speed 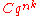 for any
for any  . As a general rule, the higher the
. As a general rule, the higher the 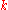 , the less stable it is, and the more computationally expensive it gets. For these reasons, higher order methods are typically not used.
, the less stable it is, and the more computationally expensive it gets. For these reasons, higher order methods are typically not used.
- Runge-Kutta methods and numerical Ordinary Differential EquationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
solvers in general can be viewed as fixed point iterations. Indeed, the core idea when analyzing the A-stability of ODE solvers is to start with the special case , where a is a complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, where a is a complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, and to check whether the ODE solver converges to the fixed point whenever the real part of a is negative.
whenever the real part of a is negative.
- The Picard–Lindelöf theoremPicard–Lindelöf theoremIn mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
, which shows that ordinary differential equations have solutions, is essentially an application of the Banach fixed point theoremBanach fixed point theoremIn mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
to a special sequence of functions which forms a fixed point iteration.
- The goal seekingGoal seekingIn computing, goal seeking is the ability to calculate backward to obtain an input that would result in a given output. This can also be called what-if analysis or back-solving. It can either be attempted through trial and improvement or more logical means...
function in Excel can be used to find solutions to the Colebrook equation to an accuracy of 15 significant figures.
- Some of the "successive approximation" schemes used in dynamic programmingDynamic programmingIn mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
to solve Bellman's functional equationBellman equationA Bellman equation , named after its discoverer, Richard Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming...
are based on fixed point iterations in the space of the return function.
Properties
If a function defined on the real line with real values is Lipschitz continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
defined on the real line with real values is Lipschitz continuousLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
with Lipschitz constant , then this function has precisely one fixed point, and the fixed-point iteration converges towards that fixed point for any initial guess
, then this function has precisely one fixed point, and the fixed-point iteration converges towards that fixed point for any initial guess  This theorem can be generalized to any metric space.
This theorem can be generalized to any metric space.
The speed of convergence of the iteration sequence can be increased by using a convergence acceleration method such as Aitken's delta-squared processAitken's delta-squared processIn numerical analysis, Aitken's delta-squared process is a series acceleration method, used for accelerating the rate of convergence of a sequence. It is named after Alexander Aitken, who introduced this method in 1926. Its early form was known to Seki Kōwa and was found for rectification of the...
. The application of Aitken's method to fixed-point iteration is known as Steffensen's methodSteffensen's methodIn numerical analysis, Steffensen's method is a root-finding method, similar to Newton's method, named after Johan Frederik Steffensen. Steffensen's method also achieves quadratic convergence, but without using derivatives as Newton's method does....
, and it can be shown that Steffensen's method yields a rate of convergence that is at least quadratic.
See also
- Root-finding algorithmRoot-finding algorithmA root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
- Fixed-point theoremFixed-point theoremIn mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point , under some conditions on F that can be stated in general terms...
- Fixed-point combinator
- Banach fixed-point theorem
- Cobweb plotCobweb plotA cobweb plot, or Verhulst diagram is a visual tool used in the dynamical systems field of mathematics to investigate the qualitative behaviour of one dimensional iterated functions, such as the logistic map...
External links
- Newton's method

