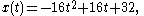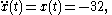Differential calculus
Encyclopedia
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, differential calculus is a subfield of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus.
The primary objects of study in differential calculus are the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, related notions such as the differential
Differential of a function
In calculus, the differential represents the principal part of the change in a function y = ƒ with respect to changes in the independent variable. The differential dy is defined bydy = f'\,dx,...
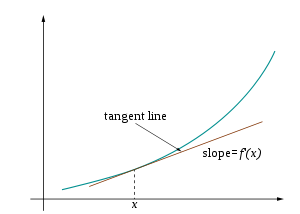
, and their applications. The derivative of a function at a chosen input value describes the rate of change of the function near that input value. The process of finding a derivative is called differentiation. Geometrically, the derivative at a point equals the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the tangent line to the graph of the function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
at that point. For a real-valued function
Real-valued function
In mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
of a single real variable, the derivative of a function at a point generally determines the best linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
to the function at that point.
Differential calculus and integral calculus are connected by the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
, which states that differentiation is the reverse process to integration.
Differentiation has applications to nearly all quantitative disciplines. For example, in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the derivative of the displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
of a moving body with respect to time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
is the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the body, and the derivative of velocity with respect to time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
is acceleration. Newton's second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
states that the derivative of the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of a body equals the force applied to the body. The reaction rate
Reaction rate
The reaction rate or speed of reaction for a reactant or product in a particular reaction is intuitively defined as how fast or slow a reaction takes place...
of a chemical reaction
Chemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
is a derivative. In operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, derivatives determine the most efficient ways to transport materials and design factories.
Derivatives are frequently used to find the maxima and minima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of a function. Equations involving derivatives are called differential equations and are fundamental in describing natural phenomena
Natural phenomenon
A natural phenomenon is a non-artificial event in the physical sense, and therefore not produced by humans, although it may affect humans . Common examples of natural phenomena include volcanic eruptions, weather, decay, gravity and erosion...
. Derivatives and their generalizations appear in many fields of mathematics, such as complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, differential geometry, measure theory and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
The derivative
Suppose that x and y are real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and that y is a function of x, that is, for every value of x, there is a corresponding value of y. This relationship is written as y = f(x). If f(x) is the equation for a straight line, then there are two real numbers m and b such that . m is called the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
and can be determined from the formula:
where the symbol Δ (the uppercase form of the Greek
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
letter Delta
Delta (letter)
Delta is the fourth letter of the Greek alphabet. In the system of Greek numerals it has a value of 4. It was derived from the Phoenician letter Dalet...
) is an abbreviation for "change in". It follows that .
A general function is not a line, so it does not have a slope. The derivative of f at the point x is the best possible approximation to the idea of the slope of f at the point x. It is usually denoted f
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
, of f near the point x. This latter property is usually taken as the definition of the derivative.
A closely related notion is the differential
Differential (calculus)
In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
of a function.
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
, which is usually denoted ∂y/∂x. The linearization of f in all directions at once is called the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
.
History of differentiation
The concept of a derivative in the sense of a tangent line is a very old one, familiar to GreekAncient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
geometers such as
Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
(c. 300 BC), Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
(c. 287–212 BC) and Apollonius of Perga
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
(c. 262–190 BC). Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
also introduced the use of infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
s, although these were primarily used to study areas and volumes rather than derivatives and tangents; see Archimedes' use of infinitesimals
Archimedes' use of infinitesimals
The Method of Mechanical Theorems is a work by Archimedes which contains the first attested explicit use of infinitesimals. The work was originally thought to be lost, but was rediscovered in the celebrated Archimedes Palimpsest...
.
The use of infinitesimals to study rates of change can be found in Indian mathematics
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
, perhaps as early as 500 AD, when the astronomer and mathematician Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
(476–550) used infinitesimals to study the motion of the moon. The use of infinitesimals to compute rates of change was developed significantly by Bhāskara II (1114–1185); indeed, it has been argued that many of the key notions of differential calculus can be found in his work, such as "Rolle's theorem
Rolle's theorem
In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...
". The Persian mathematician
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
, Sharaf al-Dīn al-Tūsī (1135–1213), was the first to discover the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of cubic polynomials
Cubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
, an important result in differential calculus; his Treatise on Equations developed concepts related to differential calculus, such as the derivative function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and the maxima and minima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of curves, in order to solve cubic equations which may not have positive solutions.
The modern development of calculus is usually credited to Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
(1643–1727) and Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
(1646–1716), who provided independent and unified approaches to differentiation and derivatives. The key insight, however, that earned them this credit, was the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
relating differentiation and integration: this rendered obsolete most previous methods for computing areas and volumes, which had not been significantly extended since the time of Ibn al-Haytham (Alhazen). For their ideas on derivatives, both Newton and Leibniz built on significant earlier work by mathematicians such as Isaac Barrow
Isaac Barrow
Isaac Barrow was an English Christian theologian, and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for the discovery of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was...
(1630–1677), René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
(1596–1650), Christiaan Huygens (1629–1695), Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
(1623–1662) and John Wallis (1616–1703). Isaac Barrow is generally given credit for the early development of the derivative. Nevertheless, Newton and Leibniz remain key figures in the history of differentiation, not least because Newton was the first to apply differentiation to theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, while Leibniz systematically developed much of the notation still used today.
Since the 17th century many mathematicians have contributed to the theory of differentiation. In the 19th century, calculus was put on a much more rigorous footing by mathematicians such as Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
(1789–1857), Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
(1826–1866), and Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
(1815–1897). It was also during this period that the differentiation was generalized to Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
Optimization
If f is a differentiable functionDifferentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
on R (or an open interval) and x is a local maximum or a local minimum of f, then the derivative of f at x is zero; points where are called critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
or stationary point
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
s (and the value of f at x is called a critical value
Critical value
-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
). (The definition of a critical point is sometimes extended to include points where the derivative does not exist.) Conversely, a critical point x of f can be analysed by considering the second derivative
Second derivative
In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
of f at x:
- if it is positive, x is a local minimum;
- if it is negative, x is a local maximum;
- if it is zero, then x could be a local minimum, a local maximum, or neither. (For example, has a critical point at , but it has neither a maximum nor a minimum there, whereas has a critical point at and a minimum and a maximum, respectively, there.)
This is called the second derivative test
Second derivative test
In calculus, the second derivative test is a criterion often useful for determining whether a given stationary point of a function is a local maximum or a local minimum using the value of the second derivative at the point....
. An alternative approach, called the first derivative test
First derivative test
In calculus, the first derivative test uses the first derivative of a function to determine whether a given critical point of a function is a local maximum, a local minimum, or neither.-Intuitive explanation:...
, involves considering the sign of the f
Taking derivatives and solving for critical points is therefore often a simple way to find local minima or maxima, which can be useful in optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
. By the extreme value theorem
Extreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
, a continuous function on a closed interval must attain its minimum and maximum values at least once. If the function is differentiable, the minima and maxima can only occur at critical points or endpoints.
This also has applications in graph sketching: once the local minima and maxima of a differentiable function have been found, a rough plot of the graph can be obtained from the observation that it will be either increasing or decreasing between critical points.
In higher dimensions, a critical point of a scalar valued function is a point at which the gradient is zero. The second derivative test can still be used to analyse critical points by considering the eigenvalues of the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of second partial derivatives of the function at the critical point. If all of the eigenvalues are positive, then the point is a local minimum; if all are negative, it is a local maximum. If there are some positive and some negative eigenvalues, then the critical point is a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
, and if none of these cases hold (i.e., some of the eigenvalues are zero) then the test is inconclusive.
Calculus of variations
One example of an optimization problem is: Find the shortest curve between two points on a surface, assuming that the curve must also lie on the surface. If the surface is a plane, then the shortest curve is a line. But if the surface is, for example, egg-shaped, then the shortest pathShortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
is not immediately clear. These paths are called geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s, and one of the simplest problems in the calculus of variations is finding geodesics. Another example is: Find the smallest area surface filling in a closed curve in space. This surface is called a minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
and it, too, can be found using the calculus of variations.
Physics
Calculus is of vital importance in physics: many physical processes are described by equations involving derivatives, called differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. Physics is particularly concerned with the way quantities change and evolve over time, and the concept of the "time derivative
Time derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t\,.-Notation:...
" — the rate of change over time — is essential for the precise definition of several important concepts. In particular, the time derivatives of an object's position are significant in Newtonian physics:
- velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
is the derivative (with respect to time) of an object's displacement (distance from the original position) - accelerationAccelerationIn physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
is the derivative (with respect to time) of an object's velocity, that is, the second derivative (with respect to time) of an object's position.
For example, if an object's position on a line is given by
then the object's velocity is
and the object's acceleration is
which is constant.
Differential equations
A differential equation is a relation between a collection of functions and their derivatives. An ordinary differential equation is a differential equation that relates functions of one variable to their derivatives with respect to that variable. A partial differential equation is a differential equation that relates functions of more than one variable to their partial derivatives. Differential equations arise naturally in the physical sciences, in mathematical modelling, and within mathematics itself. For example, Newton's second law, which describes the relationship between acceleration and force, can be stated as the ordinary differential equation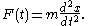
The heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
in one space variable, which describes how heat diffuses through a straight rod, is the partial differential equation
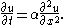
Here u(x,t) is the temperature of the rod at position x and time t and α is a constant that depends on how fast heat diffuses through the rod.
Mean value theorem
The mean value theorem gives a relationship between values of the derivative and values of the original function. If f(x) is a real-valued function and a and b are numbers with , then the mean value theorem says that under mild hypotheses, the slope between the two points (a,f(a)) and (b,f(b)) is equal to the slope of the tangent line to f at some point c between a and b. In other words,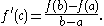
In practice, what the mean value theorem does is control a function in terms of its derivative. For instance, suppose that f has derivative equal to zero at each point. This means that its tangent line is horizontal at every point, so the function should also be horizontal. The mean value theorem proves that this must be true: The slope between any two points on the graph of f must equal the slope of one of the tangent lines of f. All of those slopes are zero, so any line from one point on the graph to another point will also have slope zero. But that says that the function does not move up or down, so it must be a horizontal line. More complicated conditions on the derivative lead to less precise but still highly useful information about the original function.
Taylor polynomials and Taylor series
The derivative gives the best possible linear approximation, but this can be very different from the original function. One way of improving the approximation is to take a quadratic approximation. That is to say, the linearization of a real-valued function f(x) at the point x0 is a linear polynomial , and it may be possible to get a better approximation by considering a quadratic polynomial . Still better might be a cubic polynomial , and this idea can be extended to arbitrarily high degree polynomials. For each one of these polynomials, there should be a best possible choice of coefficients a, b, c, and d that makes the approximation as good as possible.In the neigbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of x0, for a the best possible choice is always f(x0), and for b the best possible choice is always f
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
. Using these coefficients gives the Taylor polynomial of f. The Taylor polynomial of degree d is the polynomial of degree d which best approximates f, and its coefficients can be found by a generalization of the above formulas. Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
gives a precise bound on how good the approximation is. If f is a polynomial of degree less than or equal to d, then the Taylor polynomial of degree d equals f.
The limit of the Taylor polynomials is an infinite series called the Taylor series. The Taylor series is frequently a very good approximation to the original function. Functions which are equal to their Taylor series are called analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s. It is impossible for functions with discontinuities or sharp corners to be analytic, but there are smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s which are not analytic.
Implicit function theorem
Some natural geometric shapes, such as circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s, cannot be drawn as the graph of a function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
. For instance, if , then the circle is the set of all pairs (x,y) such that . This set is called the zero set of f. It is not the same as the graph of f, which is a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
. The implicit function theorem converts relations such as into functions. It states that if f is continuously differentiable, then around most points, the zero set of f looks like graphs of functions pasted together. The points where this is not true are determined by a condition on the derivative of f. The circle, for instance, can be pasted together from the graphs of the two functions
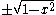. In a neighborhood of every point on the circle except (−1,0) and (1,0), one of these two functions has a graph that looks like the circle. (These two functions also happen to meet (−1,0) and (1,0), but this is not guaranteed by the implicit function theorem.)The implicit function theorem is closely related to the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
, which states when a function looks like graphs of invertible functions pasted together.
See also
- Differential (calculus)Differential (calculus)In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
- Differential geometry
- Numerical differentiationNumerical differentiationIn numerical analysis, numerical differentiation describes algorithms for estimating the derivative of a mathematical function or function subroutine using values of the function and perhaps other knowledge about the function.-Finite difference formulae:...
- Techniques for differentiation
- List of calculus topics