Chinese mathematics
Encyclopedia
Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimal
s, a place value decimal system
, a binary system
, algebra
, geometry
, and trigonometry
.
Many believe that Chinese mathematics and the mathematics of the ancient Mediterranean world had developed more or less independently up to the time when The Nine Chapters on the Mathematical Art
reached its final form, while the Writings on Reckoning and Huainanzi
preceded it. It is often suggested that some Chinese mathematical discoveries predate their Western counterparts. One example is the Pythagorean theorem
. There is some controversy regarding this issue and the precise nature of this knowledge in early China. The Chinese were one of the most advanced in dealing with mathematical computations, being the earliest to use place value decimal calculation notation, about one millennium earlier than other civilization. Elements of "Pythagorean" science have been found, for example, in one of the oldest Classical Chinese texts (see King Wen sequence
). Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal
, such as by Shen Kuo
.
Knowledge of Chinese mathematics
before 254 BC is somewhat fragmentary, and even after this date the manuscript traditions are obscure. The dating of the use of certain mathematical methods in Chinese history is problematic and disputed
In early times the focus was on astronomy
and perfecting the calendar
and not on establishing the proof
. Axiomic proof was the strength of ancient Greek mathematician; ancient Chinese mathematicians excelled at place value decimal device computation, algorithm development and algebra, the weakness of their Greek counterparts. The algorithm and algebra tradition of ancient Chinese together with the axiomic deduction of Greece formed the two equally important pillars of world mathematics. While the Greek mathematics declined in the west during the mediaval times, the achievement of Chinese algebra reached its zenith.
Simple mathematics on Oracle bone script
date back to the Shang Dynasty
(1600–1050 BC). One of the oldest surviving mathematical works is the Yi Jing
, which greatly influenced written literature during the Zhou Dynasty
(1050–256 BC). For mathematics, the book included a sophisticated use of hexagrams. Leibniz pointed out, the I Ching contained elements of
binary numbers.
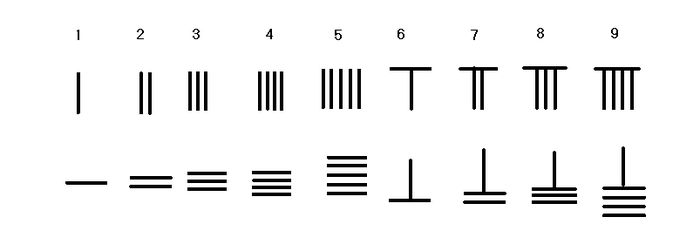
Since the Shang period, the Chinese had already fully developed a decimal
system. Since early times, Chinese understood basic arithmetic
(which dominated far eastern history), algebra
, equations, and negative numbers with counting rods
Although the Chinese were more focused on arithmetic and advanced algebra for astronomical
uses, they were also the first to develop negative numbers, algebraic geometry
(only Chinese geometry) and the usage of decimals.
Mathematics was one of the Liù Yì (六艺) or Six Arts
, students were required to master during the Zhou Dynasty
(1122–256 BC). Learning them all perfectly was required to be a perfect gentleman, or in the Chinese sense, a "Renaissance Man
". Six Arts have their roots in the Confucian philosophy.
The oldest existent work on geometry in China comes from the philosophical Mohist canon of c. 330 BC, compiled by the followers of Mozi
(470–390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small wealth of information on mathematics as well. It provided an 'atomic' definition of the geometric point, stating that a line is separated into parts, and the part which has no remaining parts (i.e. cannot be divided into smaller parts) and thus forms the extreme end of a line is a point. Much like Euclid
's first and third definitions and Plato
's 'beginning of a line', the Mo Jing stated that "a point may stand at the end (of a line) or at its beginning like a head-presentation in childbirth. (As to its invisibility) there is nothing similar to it." Similar to the atomists of Democritus
, the Mo Jing stated that a point is the smallest unit, and cannot be cut in half, since 'nothing' cannot be halved. It stated that two lines of equal length will always finish at the same place, while providing definitions for the comparison of lengths and for parallels, along with principles of space and bounded space. It also described the fact that planes without the quality of thickness cannot be piled up since they cannot mutually touch. The book provided definitions for circumference, diameter, and radius, along with the definition of volume.
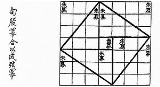
The history of mathematical development lacks some evidence. There are still debates about certain mathematical classics. For example, the Zhou Bi Suan Jing dates around 1200–1000 BC, yet many scholars believed it was written between 300–250 BC. The Zhou Bi Suan Jing contains an in-depth proof of the Gougu Theorem (Pythagorean Theorem
) but focuses more on astronomical calculations.
mathematics, or before, due to the burning of books and burying of scholars
.
Knowledge of this period must be carefully determined by their civil projects and historical evidence. The Qin dynasty created a standard system of weights. Civil projects of the Qin dynasty were incredible feats of human engineering. Emperor Qin Shihuang（秦始皇）ordered many men to build large, lifesize statues for the palace tomb along with various other temples and shrines. The shape of the tomb is designed with geometric skills of architecture. It is certain that one of the greatest feats of human history; the great wall required many mathematical "techniques." All Qin dynasty buildings and grand projects used advanced computation formulas for volume, area and proportion.
called chousuan
,consisted of only nine symbols, a blank space on the counting board stood for zero. The mathematicians Liu Xin
(d. 23) and Zhang Heng
(78–139) gave more accurate approximations for pi
than Chinese of previous centuries had used. Zhang also applied mathematics in his work in astronomy
.
(writings on reckoning) is an ancient Chinese text on mathematics approximately seven thousand characters in length, written on 190 bamboo strips. It was discovered together with other writings in 1984 when archaeologists opened a tomb at Zhangjiashan in Hubei
province. From documentary evidence this tomb is known to have been closed in 186 BC, early in the Western Han dynasty
. While its relationship to the Nine Chapters is still under discussion by scholars, some of its contents are clearly paralleled there. The text of the Suan shu shu is however much less systematic than the Nine Chapters, and appears to consist of a number of more or less independent short sections of text drawn from a number of sources. Some linguistic hints point back to the Qin dynasty
.
In an example of an elementary mathematics in the Suàn shù shū, the square root
is approximated by using an "excess and deficiency" method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend."
is a Chinese mathematics
book, its oldest archeological date being 179 AD (traditionally dated 1000 BC), but perhaps as early as 300–200 BC. Although the author(s) are unknown, they made a huge contribution in the eastern world. The methods were made for everyday life and gradually taught advanced methods. It also contains evidence of the Gaussian elimination
and Cramer's Rule
for system of linear equations.
It was one of the most influential of all Chinese mathematical books and it is composed of some 246 problems. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns. Estimates concerning the Chou Pei Suan Ching, generally considered to be the oldest of the mathematical classics, differ by almost a thousand years. A date of about 300 BC would appear reasonable, thus placing it in close competition with another treatise, the Jiu zhang suanshu, composed about 250 BC, that is, shortly before the Han dynasty (202 BC). Almost as old at the Chou Pei, and perhaps the most influential of all Chinese mathematical books, was the Jiuzhang suanshu, or Nine Chapters on the Mathematical Art. This book includes 246 problems on surveying, agriculture, partnerships, engineering, taxation, calculation, the solution of equations, and the properties of right triangles. Chapter eight of the Nine chapters is significant for its solution of problems of simultaneous linear equations, using both positive and negative numbers. The earliest known magic squares appeared in China. The Chinese were especially fond of patterns, as a natural outcome of arranging counting rods
in rows on counting board to carry out computation; hence,it is not surprising that the first record (of ancient but unknown origin) of a magic square appeared there. The concern for such patterns led the author of the Nine Chapters to solve the system of simultaneous linear equations by placing the coefficients and constant terms of the linear equations into a matrix and performing column reducing operations on the matrix to reduce it to a triangular form represented by the equations 36z = 99, 5y + z = 24, and 3x + 2y + z = 39 from which the values of z, y, and x are successively found with ease. The last problem in the chapter involves four equations in five unknowns, and the topic of indeterminate equations was to remain a favorite among Oriental peoples.
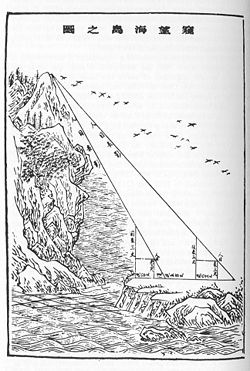In the third century Liu Hui
wrote his commentary on the Nine Chapters and also wrote Haidao suanjing which dealt with using Pythagorean theorem (already known by the 9 chapters), and triple, quadruple triangulation for surveying; his accomplishment in the mathematical surveying exceeded those accomplished in the west by a millennium. He was the first Chinese mathematician to calculate π=3.1416 with his π algorithm. He discovered the usage of Cavalieri's principle
to find an accurate formula for the volume of a cylinder, and also developed elements of the integral and the differential
calculus
during the 3rd century CE.
In the fourth century, another influential mathematician named Zu Chongzhi
, introduced the Da Ming Li. This calendar was specifically calculated to predict many cosmological cycles that will occur in a period of time. Very little is really known about his life. Today, the only sources are found in Book of Sui
, we now know that Zu Chongzhi was one of the generations of mathematicians. He used Liu Hui's pi-algorithm applied to a 12288-gon and obtained a value of pi to 7 accurate decimal places (between 3.1415926 and 3.1415927), which would remain the most accurate approximation of π available for the next 900 years. He also used He Chengtian's interpolation method for approximating irrational number with fraction in his astronomy and mathematical works, he obtained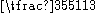
as a good fraction approximate for pi; Yoshio Mikami commented that neither the Greeks, nor the Hindus nor Arabs knew about this fraction approximation to pi, not until the Dutch mathematician Adrian Anthoniszoom rediscovered it in 1585, "the Chinese had therefore been possessed of this the most extraordinary of all fractional values over a whole millennium earlier than Europe" Along with his son, Zu Geng, Zu Chongzhi used the Cavalieri Method to find an accurate solution for calculating the volume of the sphere. His work, Zhui Shu was discarded out of the syllabus of mathematics during the Song dynasty and lost. Many believed that Zhui Shu contains the formulas and methods for linear
, matrix algebra, algorithm for calculating the value of π, formula for the volume of the sphere. The text should also associate with his astronomical methods of interpolation, which would contain knowledge, similar to our modern mathematics.
A mathematical manual called "Sunzi mathematical classic" dated around 400 CE contained the most detailed step by step description of multiplication and division algorithm with counting rods. The earliest record of multiplication and division algorithm using Hindu Arabic numerals was in writing by Al Khwarizmi in early 9th century. Khwarizmi's step by step division algorithm was completely identical to Sunzi division algorithm described in Sunzi mathematical classic four centuries earlier. Khwarizmi's work was translated in to Latin in the 13th century and spread to the west, the division algorithm later evolved into Galley division
. The route of transmission of Chinese place value decimal arithmetic know how to the west is unclear, how Sunzi's division and multiplication algorithm with rod calculus ended up in Hindu Arabic numeral form in Khwarizmi's work is unclear, as al Khwarizmi never given any Sankrit source nor quoted any Sanskrit stanza. However, the influence of rod calculus on Hindu division is evident, for example in the division example, 324 should be 32400, only rod calculus used blanks for zeros.
In the fifth century the manual called "Zhang Qiujian suanjing" discussed linear and quadratic equations. By this point the Chinese had the concept of negative numbers.
study of mathematics was fairly standard in the great schools. Wang Xiaotong
was a great mathematician in the beginning of the Tang Dynasty
, and he wrote a book: Jigu suanjing (Continuation of Ancient Mathematics), in which cubic equations
appear for the first time
The Tibetans obtained their first knowledge of mathematics (arithmetic) from China during the reign of gNam-ri srong btsan
, who died in 630.
The table
of sines by the Indian mathematician
, Aryabhata
, were translated into the Chinese mathematical book of the Kaiyuan Zhanjing
, compiled in 718 AD during the Tang Dynasty. Although the Chinese excelled in other fields of mathematics such as solid geometry
, binomial theorem
, and complex algebra
ic formulas. However,early forms of trigonometry
were not as widely appreciated as in the contemporary Indian and Islamic mathematics
. I-Xing, the mathematician and Buddhist monk was credited for calculating the tangent table. Instead, the early Chinese used an empirical
substitute known as chong cha, while practical use of plane trigonometry in using the sine, the tangent, and the secant were known.
developed an additive multiplicative method for extraction of square root and cubic root which implemented the "Horner" rule.
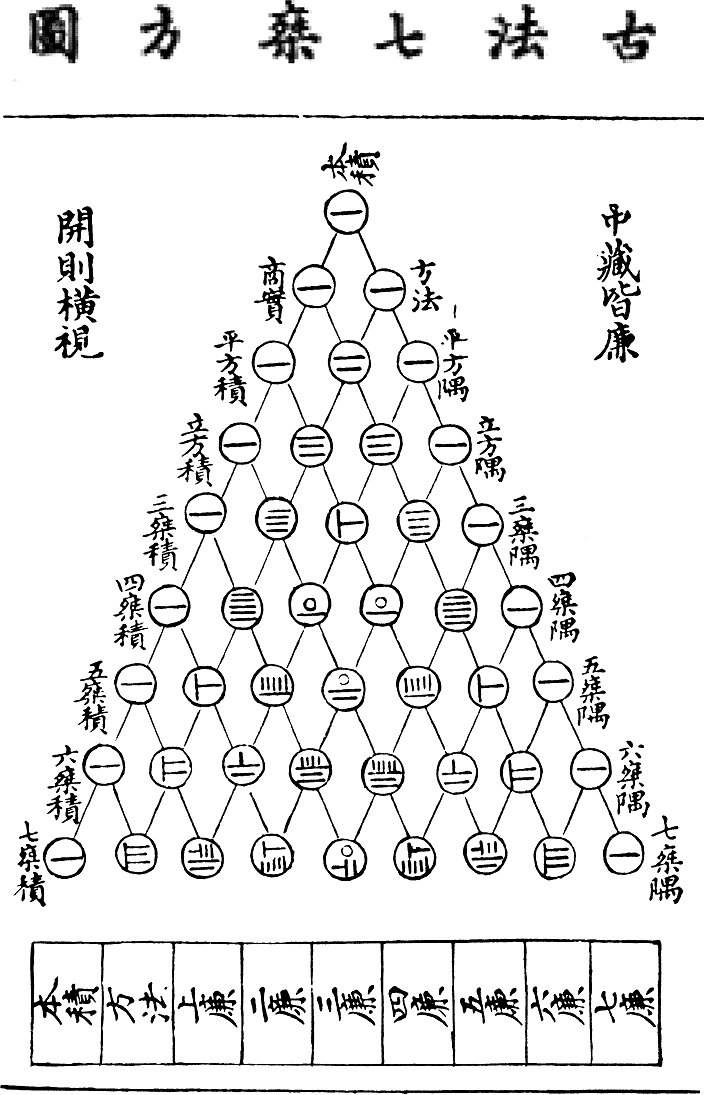
Four outstanding mathematicians arose during the Song Dynasty
and Yuan Dynasty
, particularly in the twelfth and thirteenth centuries: Yang Hui
, Qin Jiushao, Li Zhi
(Li Ye), and Zhu Shijie
. Yang Hui, Qin Jiushao, Zhu Shijie all used the Horner
-Ruffini
method six hundred years earlier to solve certain types of simultaneous equations, roots, quadratic, cubic, and quartic equations. Yang Hui was also the first person in history to discover and prove "Pascal's Triangle
", along with its binomial proof (although the earliest mention of the Pascal's triangle in China exists before the eleventh century AD). Li Zhi on the other hand, investigated on a form of algebraic geometry. His book; Ce Hai Yuan Jing revolutionized the idea of inscribing a circle into triangles, which could be calculated using equations with the Pythagorean theorem. Guo Shoujing of this era also worked on spherical trigonometry for precise astronomical calculations. At this point of mathematical history, a lot of modern western mathematics were already discovered by Chinese mathematicians.
Things grew quiet for a time until the thirteenth century Renaissance of Chinese math. This saw Chinese mathematicians solving equations with methods Europe would not know until the eighteenth century. The high point of this era came with Zhu Shijie
's two books Suanxue qimeng and the Siyuan yujian. In one case he reportedly gave a method equivalent to Gauss
's pivotal condensation.
Qin Jiushao (c. 1202–1261) was the first to introduce the zero symbol
into Chinese mathematics. Before this innovation, blank spaces were used instead of zeros in the system of counting rods
. One of the most important contribution of Qin Jiushao was his method of solving high order numerical equations. Referring to Qin's solution of a 4th order equation, Yoshio Mikami put it:" Who can deny the fact of Horner's illustrious process being used in China at least nearly six long centuries earlier than in Europe ?". Qin also solved a 10th order equation
Pascal's triangle
was first illustrated in China by Yang Hui in his book Xiangjie Jiuzhang Suanfa (详解九章算法), although it was described earlier around 1100 by Jia Xian
. Although the Introduction to Computational Studies (算学启蒙) written by Zhu Shijie
(fl.
13th century) in 1299 contained nothing new in Chinese algebra
, it had a great impact on the development of Japanese mathematics
.
The Precious Mirror opens with a diagram of the arithmetic triangle (Pascal's triangle) using a round zero symbol, but Chu Shih-chieh denies credit for it. A similar triangle appears in Yang Hui's work, but without the zero symbol.
There are many summation series equations given without proof in the Precious mirror. A few of the summation series are:
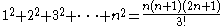
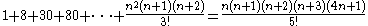
(or Li Ye) (1192–1272 AD). He used fan fa, or Horner's method, to solve equations of degree as high as six, although he did not describe his method of solving equations.
Shu-shu chiu-chang, or Mathematical Treatise in Nine Sections
, was written by the wealthy governor and minister Ch'in Chiu-shao
(ca. 1202 – ca. 1261 AD) and with the invention of a method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.
The earliest known magic square
s of order greater than three are attributed to Yang Hui
(fl. ca. 1261–1275), who worked with magic squares of order as high as ten. He also worked with magic circle
.
in China slowly began to change and advance during the Song Dynasty (960–1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendarical science and astronomical calculations. The polymath
Chinese scientist, mathematician and official Shen Kuo
(1031–1095) used trigonometric functions to solve mathematical problems of chords and arcs. Victor J. Katz writes that in Shen's formula "technique of intersecting circles", he created an approximation of the arc of a circle s by s = c + 2v2/d, where d is the diameter
, v is the versine
, c is the length of the chord c subtending the arc. Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry
developed in the 13th century by the mathematician and astronomer Guo Shoujing
(1231–1316). As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry
in his calculations to improve the calendar system
and Chinese astronomy
. Along with a later 17th century Chinese illustration of Guo's mathematical proofs, Needham states that:
However after the overthrow of the Yuan Dynasty
China became suspicious of knowledge it used. The Ming Dynasty
turned away from math and physics in favor of botany
and pharmacology
.
At this period, the abacus
which first appeared in Song dynasty now overtook the counting rods and became the preferred computing device. Zhu Zaiyu, Prince of Zheng who invented the equal temperament
used 81 position abacus to calculate the square root and cubic root of 2 to 25 figure accuracy.
However, this switching from counting rods to abacus to gain speed in calculation was at a high cost, causing the stagnation and decline of
Chinese mathematics. The pattern rich layout of counting rod numerals on counting board inspired many Chinese inventions in mathematics,such
as cross multiply principe of fractions, method for solving linear equations. The pattern rich counting rods inspired Japanese mathematician
to invent the concept of matrix. In Ming dynasty, mathematicians were fascinated with perfecting algorithms for abacus, many mathematical works
devoted to abacus mathematics appeared in this period, at the expense of new ideas creation.
Despite the achievements of Shen and Guo's work in trigonometry, another substantial work in Chinese trigonometry would not be published again until 1607, with the dual publication of Euclid's Elements
by Chinese official and astronomer Xu Guangqi
(1562–1633) and the Italian Jesuit Matteo Ricci
(1552–1610).
A revival of math in China began in the late nineteenth century, Joseph Edkins
, Alexander Wylie and Li Shanlan
translated works on astronomy, algebra and differential-integral calculus into Chinese, published by London Missionary Press in Shanghai.
Zhoubi Suanjing" c. 1000 BCE-100 CE
-Astronomical theories, and computation techniques
-Proof of the Pythagorean theorem (Shang Gao Theorem)
-Fractional computations
-Pythagorean theorem for astronomical purposes
Nine Chapters of Mathematical Arts1000 BCE? – 50 CE
-ch.1, computational algorithm, area of plane figures, GCF, LCD
-ch.2, proportions
-ch.3, proportions
-ch.4, square, cube roots, finding unknowns
-ch.5, volume and usage of pi as 3
-ch.6, proportions
-ch,7, interdeterminate equations
-ch.8, Gaussian elimination and matrices
-ch.9, Pythagorean theorem (Gougu Theorem)
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
s, a place value decimal system
Decimal system
Decimal system may refer to:* The decimal number system, used in mathematics for writing numbers and performing arithmetic.* The Dewey Decimal System, a subject classification system used in libraries....
, a binary system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
, algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
.
Many believe that Chinese mathematics and the mathematics of the ancient Mediterranean world had developed more or less independently up to the time when The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
reached its final form, while the Writings on Reckoning and Huainanzi
Huainanzi
The Huáinánzǐ is a 2nd century BCE Chinese philosophical classic from the Han dynasty that blends Daoist, Confucianist, and Legalist concepts, including theories such as Yin-Yang and the Five Phases. It was written under the patronage of Liu An, Prince of Huainan, a legendarily prodigious author...
preceded it. It is often suggested that some Chinese mathematical discoveries predate their Western counterparts. One example is the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. There is some controversy regarding this issue and the precise nature of this knowledge in early China. The Chinese were one of the most advanced in dealing with mathematical computations, being the earliest to use place value decimal calculation notation, about one millennium earlier than other civilization. Elements of "Pythagorean" science have been found, for example, in one of the oldest Classical Chinese texts (see King Wen sequence
King Wen sequence
The King Wen sequence is an arrangement of the sixty-four divination figures in 易經 Yì Jīng, the I Ching or Book of Changes. They are called hexagrams in English because each figure is composed of six 爻 yáo—broken or unbroken lines, that represent 陰 yin or 陽 yang respectively.The King Wen sequence...
). Knowledge of Pascal's triangle has also been shown to have existed in China centuries before Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
, such as by Shen Kuo
Shen Kuo
Shen Kuo or Shen Gua , style name Cunzhong and pseudonym Mengqi Weng , was a polymathic Chinese scientist and statesman of the Song Dynasty...
.
Knowledge of Chinese mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
before 254 BC is somewhat fragmentary, and even after this date the manuscript traditions are obscure. The dating of the use of certain mathematical methods in Chinese history is problematic and disputed
In early times the focus was on astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and perfecting the calendar
Calendar
A calendar is a system of organizing days for social, religious, commercial, or administrative purposes. This is done by giving names to periods of time, typically days, weeks, months, and years. The name given to each day is known as a date. Periods in a calendar are usually, though not...
and not on establishing the proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
. Axiomic proof was the strength of ancient Greek mathematician; ancient Chinese mathematicians excelled at place value decimal device computation, algorithm development and algebra, the weakness of their Greek counterparts. The algorithm and algebra tradition of ancient Chinese together with the axiomic deduction of Greece formed the two equally important pillars of world mathematics. While the Greek mathematics declined in the west during the mediaval times, the achievement of Chinese algebra reached its zenith.
Early Chinese mathematics
Oracle bone script
Oracle bone script refers to incised ancient Chinese characters found on oracle bones, which are animal bones or turtle shells used in divination in Bronze Age China...
date back to the Shang Dynasty
Shang Dynasty
The Shang Dynasty or Yin Dynasty was, according to traditional sources, the second Chinese dynasty, after the Xia. They ruled in the northeastern regions of the area known as "China proper" in the Yellow River valley...
(1600–1050 BC). One of the oldest surviving mathematical works is the Yi Jing
I Ching
The I Ching or "Yì Jīng" , also known as the Classic of Changes, Book of Changes and Zhouyi, is one of the oldest of the Chinese classic texts...
, which greatly influenced written literature during the Zhou Dynasty
Zhou Dynasty
The Zhou Dynasty was a Chinese dynasty that followed the Shang Dynasty and preceded the Qin Dynasty. Although the Zhou Dynasty lasted longer than any other dynasty in Chinese history, the actual political and military control of China by the Ji family lasted only until 771 BC, a period known as...
(1050–256 BC). For mathematics, the book included a sophisticated use of hexagrams. Leibniz pointed out, the I Ching contained elements of
binary numbers.
Since the Shang period, the Chinese had already fully developed a decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
system. Since early times, Chinese understood basic arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
(which dominated far eastern history), algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, equations, and negative numbers with counting rods
Counting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
Although the Chinese were more focused on arithmetic and advanced algebra for astronomical
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
uses, they were also the first to develop negative numbers, algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
(only Chinese geometry) and the usage of decimals.
Mathematics was one of the Liù Yì (六艺) or Six Arts
Six Arts
The Six Arts formed the basis of education in ancient Chinese culture. During the Zhou Dynasty , students were required to master the "liù yì" :# Rites# Music# Archery# Charioteering# Calligraphy# Mathematics...
, students were required to master during the Zhou Dynasty
Zhou Dynasty
The Zhou Dynasty was a Chinese dynasty that followed the Shang Dynasty and preceded the Qin Dynasty. Although the Zhou Dynasty lasted longer than any other dynasty in Chinese history, the actual political and military control of China by the Ji family lasted only until 771 BC, a period known as...
(1122–256 BC). Learning them all perfectly was required to be a perfect gentleman, or in the Chinese sense, a "Renaissance Man
Polymath
A polymath is a person whose expertise spans a significant number of different subject areas. In less formal terms, a polymath may simply be someone who is very knowledgeable...
". Six Arts have their roots in the Confucian philosophy.
The oldest existent work on geometry in China comes from the philosophical Mohist canon of c. 330 BC, compiled by the followers of Mozi
Mozi
Mozi |Lat.]] as Micius, ca. 470 BC – ca. 391 BC), original name Mo Di , was a Chinese philosopher during the Hundred Schools of Thought period . Born in Tengzhou, Shandong Province, China, he founded the school of Mohism, and argued strongly against Confucianism and Daoism...
(470–390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small wealth of information on mathematics as well. It provided an 'atomic' definition of the geometric point, stating that a line is separated into parts, and the part which has no remaining parts (i.e. cannot be divided into smaller parts) and thus forms the extreme end of a line is a point. Much like Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's first and third definitions and Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
's 'beginning of a line', the Mo Jing stated that "a point may stand at the end (of a line) or at its beginning like a head-presentation in childbirth. (As to its invisibility) there is nothing similar to it." Similar to the atomists of Democritus
Democritus
Democritus was an Ancient Greek philosopher born in Abdera, Thrace, Greece. He was an influential pre-Socratic philosopher and pupil of Leucippus, who formulated an atomic theory for the cosmos....
, the Mo Jing stated that a point is the smallest unit, and cannot be cut in half, since 'nothing' cannot be halved. It stated that two lines of equal length will always finish at the same place, while providing definitions for the comparison of lengths and for parallels, along with principles of space and bounded space. It also described the fact that planes without the quality of thickness cannot be piled up since they cannot mutually touch. The book provided definitions for circumference, diameter, and radius, along with the definition of volume.
The history of mathematical development lacks some evidence. There are still debates about certain mathematical classics. For example, the Zhou Bi Suan Jing dates around 1200–1000 BC, yet many scholars believed it was written between 300–250 BC. The Zhou Bi Suan Jing contains an in-depth proof of the Gougu Theorem (Pythagorean Theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
) but focuses more on astronomical calculations.
Qin mathematics
Not much is known about Qin dynastyQin Dynasty
The Qin Dynasty was the first imperial dynasty of China, lasting from 221 to 207 BC. The Qin state derived its name from its heartland of Qin, in modern-day Shaanxi. The strength of the Qin state was greatly increased by the legalist reforms of Shang Yang in the 4th century BC, during the Warring...
mathematics, or before, due to the burning of books and burying of scholars
Burning of books and burying of scholars
Burning of the books and burying of the scholars is a phrase that refers to a policy and a sequence of events in the Qin Dynasty of Ancient China, between the period of 213 and 206 BC. During these events, the Hundred Schools of Thought were pruned; legalism survived...
.
Knowledge of this period must be carefully determined by their civil projects and historical evidence. The Qin dynasty created a standard system of weights. Civil projects of the Qin dynasty were incredible feats of human engineering. Emperor Qin Shihuang（秦始皇）ordered many men to build large, lifesize statues for the palace tomb along with various other temples and shrines. The shape of the tomb is designed with geometric skills of architecture. It is certain that one of the greatest feats of human history; the great wall required many mathematical "techniques." All Qin dynasty buildings and grand projects used advanced computation formulas for volume, area and proportion.
Han mathematics
In the Han Dynasty, numbers were developed into a place value decimal system and used on a counting board with a set of counting rodsCounting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
called chousuan
Rod calculus
Rod calculus or rod calculation is the method of mathematical computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were replaced by the more convenient and faster abacus.-Hardware:...
,consisted of only nine symbols, a blank space on the counting board stood for zero. The mathematicians Liu Xin
Liu Xin
Liu Xin , later changed name to Liu Xiu , courtesy name Zijun , was a Chinese astronomer, historian, and editor during the Xin Dynasty . He was the son of Confucian scholar Liu Xiang and an associate of other prominent thinkers such as the philosopher Huan Tan...
(d. 23) and Zhang Heng
Zhang Heng
Zhang Heng was a Chinese astronomer, mathematician, inventor, geographer, cartographer, artist, poet, statesman, and literary scholar from Nanyang, Henan. He lived during the Eastern Han Dynasty of China. He was educated in the capital cities of Luoyang and Chang'an, and began his career as a...
(78–139) gave more accurate approximations for pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
than Chinese of previous centuries had used. Zhang also applied mathematics in his work in astronomy
Chinese astronomy
Astronomy in China has a very long history, with historians considering that "they [the Chinese] were the most persistent and accurate observers of celestial phenomena anywhere in the world before the Arabs."...
.
Suan shu shu
The Suàn shù shūSuàn shù shu
The Suàn shù shū , or the Writings on Reckoning , is one of the earliest known Chinese mathematical treatises...
(writings on reckoning) is an ancient Chinese text on mathematics approximately seven thousand characters in length, written on 190 bamboo strips. It was discovered together with other writings in 1984 when archaeologists opened a tomb at Zhangjiashan in Hubei
Hubei
' Hupeh) is a province in Central China. The name of the province means "north of the lake", referring to its position north of Lake Dongting...
province. From documentary evidence this tomb is known to have been closed in 186 BC, early in the Western Han dynasty
Han Dynasty
The Han Dynasty was the second imperial dynasty of China, preceded by the Qin Dynasty and succeeded by the Three Kingdoms . It was founded by the rebel leader Liu Bang, known posthumously as Emperor Gaozu of Han. It was briefly interrupted by the Xin Dynasty of the former regent Wang Mang...
. While its relationship to the Nine Chapters is still under discussion by scholars, some of its contents are clearly paralleled there. The text of the Suan shu shu is however much less systematic than the Nine Chapters, and appears to consist of a number of more or less independent short sections of text drawn from a number of sources. Some linguistic hints point back to the Qin dynasty
Qin Dynasty
The Qin Dynasty was the first imperial dynasty of China, lasting from 221 to 207 BC. The Qin state derived its name from its heartland of Qin, in modern-day Shaanxi. The strength of the Qin state was greatly increased by the legalist reforms of Shang Yang in the 4th century BC, during the Warring...
.
In an example of an elementary mathematics in the Suàn shù shū, the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
is approximated by using an "excess and deficiency" method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend."
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical ArtThe Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
is a Chinese mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
book, its oldest archeological date being 179 AD (traditionally dated 1000 BC), but perhaps as early as 300–200 BC. Although the author(s) are unknown, they made a huge contribution in the eastern world. The methods were made for everyday life and gradually taught advanced methods. It also contains evidence of the Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
and Cramer's Rule
Cramer's rule
In linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
for system of linear equations.
It was one of the most influential of all Chinese mathematical books and it is composed of some 246 problems. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns. Estimates concerning the Chou Pei Suan Ching, generally considered to be the oldest of the mathematical classics, differ by almost a thousand years. A date of about 300 BC would appear reasonable, thus placing it in close competition with another treatise, the Jiu zhang suanshu, composed about 250 BC, that is, shortly before the Han dynasty (202 BC). Almost as old at the Chou Pei, and perhaps the most influential of all Chinese mathematical books, was the Jiuzhang suanshu, or Nine Chapters on the Mathematical Art. This book includes 246 problems on surveying, agriculture, partnerships, engineering, taxation, calculation, the solution of equations, and the properties of right triangles. Chapter eight of the Nine chapters is significant for its solution of problems of simultaneous linear equations, using both positive and negative numbers. The earliest known magic squares appeared in China. The Chinese were especially fond of patterns, as a natural outcome of arranging counting rods
Counting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
in rows on counting board to carry out computation; hence,it is not surprising that the first record (of ancient but unknown origin) of a magic square appeared there. The concern for such patterns led the author of the Nine Chapters to solve the system of simultaneous linear equations by placing the coefficients and constant terms of the linear equations into a matrix and performing column reducing operations on the matrix to reduce it to a triangular form represented by the equations 36z = 99, 5y + z = 24, and 3x + 2y + z = 39 from which the values of z, y, and x are successively found with ease. The last problem in the chapter involves four equations in five unknowns, and the topic of indeterminate equations was to remain a favorite among Oriental peoples.
Mathematics in the period of disunity
Liu Hui
Liu Hui was a mathematician of the state of Cao Wei during the Three Kingdoms period of Chinese history. In 263, he edited and published a book with solutions to mathematical problems presented in the famous Chinese book of mathematic known as The Nine Chapters on the Mathematical Art .He was a...
wrote his commentary on the Nine Chapters and also wrote Haidao suanjing which dealt with using Pythagorean theorem (already known by the 9 chapters), and triple, quadruple triangulation for surveying; his accomplishment in the mathematical surveying exceeded those accomplished in the west by a millennium. He was the first Chinese mathematician to calculate π=3.1416 with his π algorithm. He discovered the usage of Cavalieri's principle
Cavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
to find an accurate formula for the volume of a cylinder, and also developed elements of the integral and the differential
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
during the 3rd century CE.
In the fourth century, another influential mathematician named Zu Chongzhi
Zu Chongzhi
Zu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
, introduced the Da Ming Li. This calendar was specifically calculated to predict many cosmological cycles that will occur in a period of time. Very little is really known about his life. Today, the only sources are found in Book of Sui
Book of Sui
The Book of Sui was the official history of the Chinese dynasty Sui Dynasty, and it ranks among the official Twenty-Four Histories of imperial China. It was compiled by a team of historians led by the Tang Dynasty official Wei Zheng and was completed in 636.-External links:* of the Book of Sui,...
, we now know that Zu Chongzhi was one of the generations of mathematicians. He used Liu Hui's pi-algorithm applied to a 12288-gon and obtained a value of pi to 7 accurate decimal places (between 3.1415926 and 3.1415927), which would remain the most accurate approximation of π available for the next 900 years. He also used He Chengtian's interpolation method for approximating irrational number with fraction in his astronomy and mathematical works, he obtained
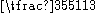as a good fraction approximate for pi; Yoshio Mikami commented that neither the Greeks, nor the Hindus nor Arabs knew about this fraction approximation to pi, not until the Dutch mathematician Adrian Anthoniszoom rediscovered it in 1585, "the Chinese had therefore been possessed of this the most extraordinary of all fractional values over a whole millennium earlier than Europe" Along with his son, Zu Geng, Zu Chongzhi used the Cavalieri Method to find an accurate solution for calculating the volume of the sphere. His work, Zhui Shu was discarded out of the syllabus of mathematics during the Song dynasty and lost. Many believed that Zhui Shu contains the formulas and methods for linearLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, matrix algebra, algorithm for calculating the value of π, formula for the volume of the sphere. The text should also associate with his astronomical methods of interpolation, which would contain knowledge, similar to our modern mathematics.
A mathematical manual called "Sunzi mathematical classic" dated around 400 CE contained the most detailed step by step description of multiplication and division algorithm with counting rods. The earliest record of multiplication and division algorithm using Hindu Arabic numerals was in writing by Al Khwarizmi in early 9th century. Khwarizmi's step by step division algorithm was completely identical to Sunzi division algorithm described in Sunzi mathematical classic four centuries earlier. Khwarizmi's work was translated in to Latin in the 13th century and spread to the west, the division algorithm later evolved into Galley division
Galley division
In arithmetic, the galley method, also known as the batello or the scratch method, was the most widely used method of division in use prior to 1600. The names galea and batello refer to a boat which the outline of the work was thought to resemble.An earlier version of this method was used as early...
. The route of transmission of Chinese place value decimal arithmetic know how to the west is unclear, how Sunzi's division and multiplication algorithm with rod calculus ended up in Hindu Arabic numeral form in Khwarizmi's work is unclear, as al Khwarizmi never given any Sankrit source nor quoted any Sanskrit stanza. However, the influence of rod calculus on Hindu division is evident, for example in the division example, 324 should be 32400, only rod calculus used blanks for zeros.
In the fifth century the manual called "Zhang Qiujian suanjing" discussed linear and quadratic equations. By this point the Chinese had the concept of negative numbers.
Tang mathematics
By the Tang DynastyTang Dynasty
The Tang Dynasty was an imperial dynasty of China preceded by the Sui Dynasty and followed by the Five Dynasties and Ten Kingdoms Period. It was founded by the Li family, who seized power during the decline and collapse of the Sui Empire...
study of mathematics was fairly standard in the great schools. Wang Xiaotong
Wang Xiaotong
Wang Xiaotong , also known as Wang Hs'iao-t'ung, was a Chinese mathematician and calendarist. He is famous as the author of the Jigu Suanjing one of the Ten Computational Canons....
was a great mathematician in the beginning of the Tang Dynasty
Tang Dynasty
The Tang Dynasty was an imperial dynasty of China preceded by the Sui Dynasty and followed by the Five Dynasties and Ten Kingdoms Period. It was founded by the Li family, who seized power during the decline and collapse of the Sui Empire...
, and he wrote a book: Jigu suanjing (Continuation of Ancient Mathematics), in which cubic equations
appear for the first time
The Tibetans obtained their first knowledge of mathematics (arithmetic) from China during the reign of gNam-ri srong btsan
Namri Songtsen
Namri Songtsen , also known as "Namri Löntsen" was, according to tradition, the 32nd King of Tibet , despite the fact he formerly ruled only the Yarlung valley, and later the central part of the Tibetan plateau...
, who died in 630.
The table
Āryabhaṭa's sine table
Āryabhaṭa's sine table is a set of twenty-four of numbers given in the astronomical treatise Āryabhaṭiya composed by the fifth century Indian mathematician and astronomer Āryabhaṭa , for the computation of the half-chords of certain set of arcs of a circle...
of sines by the Indian mathematician
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
, Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
, were translated into the Chinese mathematical book of the Kaiyuan Zhanjing
Treatise on Astrology of the Kaiyuan Era
The Treatise on Astrology of the Kaiyuan Era is a Chinese astrology encyclopedia compiled by the lead editor Gautama Siddha and numerous scholars from 714 to 724 AD during the Kaiyuan era of Tang Dynasty. The compilation is attributed to the author by 729. Its full title is regarded as the Great...
, compiled in 718 AD during the Tang Dynasty. Although the Chinese excelled in other fields of mathematics such as solid geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, and complex algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic formulas. However,early forms of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
were not as widely appreciated as in the contemporary Indian and Islamic mathematics
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
. I-Xing, the mathematician and Buddhist monk was credited for calculating the tangent table. Instead, the early Chinese used an empirical
Empirical
The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....
substitute known as chong cha, while practical use of plane trigonometry in using the sine, the tangent, and the secant were known.
Song and Yuan mathematics
Northern Song Dynasty mathematician Jia XianJia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
developed an additive multiplicative method for extraction of square root and cubic root which implemented the "Horner" rule.
Song Dynasty
The Song Dynasty was a ruling dynasty in China between 960 and 1279; it succeeded the Five Dynasties and Ten Kingdoms Period, and was followed by the Yuan Dynasty. It was the first government in world history to issue banknotes or paper money, and the first Chinese government to establish a...
and Yuan Dynasty
Yuan Dynasty
The Yuan Dynasty , or Great Yuan Empire was a ruling dynasty founded by the Mongol leader Kublai Khan, who ruled most of present-day China, all of modern Mongolia and its surrounding areas, lasting officially from 1271 to 1368. It is considered both as a division of the Mongol Empire and as an...
, particularly in the twelfth and thirteenth centuries: Yang Hui
Yang Hui
Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...
, Qin Jiushao, Li Zhi
Li Zhi (mathematician)
Li Zhi , later Li Ye , was a Chinese mathematician and scholar, who published and improved the tian yuan shu method for solving polynomial equations of one variable.- Name :...
(Li Ye), and Zhu Shijie
Zhu Shijie
Zhu Shijie , courtesy name Hanqing , pseudonym Songting , was one of the greatest Chinese mathematicians lived during the Yuan Dynasty....
. Yang Hui, Qin Jiushao, Zhu Shijie all used the Horner
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
-Ruffini
Ruffini's rule
In mathematics, Ruffini's rule allows the rapid division of any polynomial by a binomial of the form x − r. It was described by Paolo Ruffini in 1809. Ruffini's rule is a special case of synthetic division when the divisor is a linear factor. The Horner scheme is a fast algorithm for dividing...
method six hundred years earlier to solve certain types of simultaneous equations, roots, quadratic, cubic, and quartic equations. Yang Hui was also the first person in history to discover and prove "Pascal's Triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
", along with its binomial proof (although the earliest mention of the Pascal's triangle in China exists before the eleventh century AD). Li Zhi on the other hand, investigated on a form of algebraic geometry. His book; Ce Hai Yuan Jing revolutionized the idea of inscribing a circle into triangles, which could be calculated using equations with the Pythagorean theorem. Guo Shoujing of this era also worked on spherical trigonometry for precise astronomical calculations. At this point of mathematical history, a lot of modern western mathematics were already discovered by Chinese mathematicians.
Things grew quiet for a time until the thirteenth century Renaissance of Chinese math. This saw Chinese mathematicians solving equations with methods Europe would not know until the eighteenth century. The high point of this era came with Zhu Shijie
Zhu Shijie
Zhu Shijie , courtesy name Hanqing , pseudonym Songting , was one of the greatest Chinese mathematicians lived during the Yuan Dynasty....
's two books Suanxue qimeng and the Siyuan yujian. In one case he reportedly gave a method equivalent to Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
's pivotal condensation.
Qin Jiushao (c. 1202–1261) was the first to introduce the zero symbol
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
into Chinese mathematics. Before this innovation, blank spaces were used instead of zeros in the system of counting rods
Counting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
. One of the most important contribution of Qin Jiushao was his method of solving high order numerical equations. Referring to Qin's solution of a 4th order equation, Yoshio Mikami put it:" Who can deny the fact of Horner's illustrious process being used in China at least nearly six long centuries earlier than in Europe ?". Qin also solved a 10th order equation
Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
was first illustrated in China by Yang Hui in his book Xiangjie Jiuzhang Suanfa (详解九章算法), although it was described earlier around 1100 by Jia Xian
Jia Xian
Jia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
. Although the Introduction to Computational Studies (算学启蒙) written by Zhu Shijie
Zhu Shijie
Zhu Shijie , courtesy name Hanqing , pseudonym Songting , was one of the greatest Chinese mathematicians lived during the Yuan Dynasty....
(fl.
Floruit
Floruit , abbreviated fl. , is a Latin verb meaning "flourished", denoting the period of time during which something was active...
13th century) in 1299 contained nothing new in Chinese algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, it had a great impact on the development of Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
.
Precious Mirror of the Four Elements
Si-yüan yü-jian《四元玉鑒》, or Precious Mirror of the Four Elements, was written by Chu Shi-jie in 1303 AD and it marks the peak in the development of Chinese algebra. The four elements, called heaven, earth, man and matter, represented the four unknown quantities in his algebraic equations. The Ssy-yüan yü-chien deals with simultaneous equations and with equations of degrees as high as fourteen. The author uses the method of fan fa, today called Horner's method, to solve these equations.The Precious Mirror opens with a diagram of the arithmetic triangle (Pascal's triangle) using a round zero symbol, but Chu Shih-chieh denies credit for it. A similar triangle appears in Yang Hui's work, but without the zero symbol.
There are many summation series equations given without proof in the Precious mirror. A few of the summation series are:
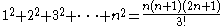
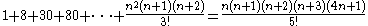
Algebra
Ts'e-yuan hai-ching (pinyin: Cèyuán Hǎijìng) (Chinese characters:測圓海鏡), or Sea-Mirror of the Circle Measurements, is a collection of some 170 problems written by Li ZhiLi Zhi (mathematician)
Li Zhi , later Li Ye , was a Chinese mathematician and scholar, who published and improved the tian yuan shu method for solving polynomial equations of one variable.- Name :...
(or Li Ye) (1192–1272 AD). He used fan fa, or Horner's method, to solve equations of degree as high as six, although he did not describe his method of solving equations.
Shu-shu chiu-chang, or Mathematical Treatise in Nine Sections
Mathematical Treatise in Nine Sections
The Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
, was written by the wealthy governor and minister Ch'in Chiu-shao
Ch'in Chiu-Shao
Qin Jiushao , courtesy name Daogu , was a Chinese mathematician.- Biography :He was born in Ziyang, Sichuan, his ancestry was from Shandong, and is now regarded as one of the greatest mathematicians of the 13th century. This is particularly remarkable, as Qin did not devote his life to mathematics...
(ca. 1202 – ca. 1261 AD) and with the invention of a method of solving simultaneous congruences, it marks the high point in Chinese indeterminate analysis.
The earliest known magic square
Magic square
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
s of order greater than three are attributed to Yang Hui
Yang Hui
Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...
(fl. ca. 1261–1275), who worked with magic squares of order as high as ten. He also worked with magic circle
Magic circle (mathematics)
Magic circles were invented by the Song Dynasty Chinese mathematician Yang Hui . It is the arrangement of natural numbers on circles where the sum of the numbers on each circle and the sum of numbers on diameter are identical...
.
Trigonometry
The embryonic state of trigonometryTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
in China slowly began to change and advance during the Song Dynasty (960–1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendarical science and astronomical calculations. The polymath
Polymath
A polymath is a person whose expertise spans a significant number of different subject areas. In less formal terms, a polymath may simply be someone who is very knowledgeable...
Chinese scientist, mathematician and official Shen Kuo
Shen Kuo
Shen Kuo or Shen Gua , style name Cunzhong and pseudonym Mengqi Weng , was a polymathic Chinese scientist and statesman of the Song Dynasty...
(1031–1095) used trigonometric functions to solve mathematical problems of chords and arcs. Victor J. Katz writes that in Shen's formula "technique of intersecting circles", he created an approximation of the arc of a circle s by s = c + 2v2/d, where d is the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
, v is the versine
Versine
The versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
, c is the length of the chord c subtending the arc. Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
developed in the 13th century by the mathematician and astronomer Guo Shoujing
Guo Shoujing
Guo Shoujing , courtesy name Ruosi , was a Chinese astronomer, engineer, and mathematician born in Xingtai, Hebei who lived during the Yuan Dynasty...
(1231–1316). As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
in his calculations to improve the calendar system
Chinese calendar
The Chinese calendar is a lunisolar calendar, incorporating elements of a lunar calendar with those of a solar calendar. It is not exclusive to China, but followed by many other Asian cultures as well...
and Chinese astronomy
Chinese astronomy
Astronomy in China has a very long history, with historians considering that "they [the Chinese] were the most persistent and accurate observers of celestial phenomena anywhere in the world before the Arabs."...
. Along with a later 17th century Chinese illustration of Guo's mathematical proofs, Needham states that:
Guo used a quadrangular spherical pyramid, the basal quadrilateral of which consisted of one equatorial and one ecliptic arc, together with two meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
s, one of which passed through the summer solsticeSummer solsticeThe summer solstice occurs exactly when the axial tilt of a planet's semi-axis in a given hemisphere is most inclined towards the star that it orbits. Earth's maximum axial tilt to our star, the Sun, during a solstice is 23° 26'. Though the summer solstice is an instant in time, the term is also...
point...By such methods he was able to obtain the du lü (degrees of equator corresponding to degrees of ecliptic), the ji cha (values of chords for given ecliptic arcs), and the cha lü (difference between chords of arcs differing by 1 degree).
Later developments
Yuan Dynasty
The Yuan Dynasty , or Great Yuan Empire was a ruling dynasty founded by the Mongol leader Kublai Khan, who ruled most of present-day China, all of modern Mongolia and its surrounding areas, lasting officially from 1271 to 1368. It is considered both as a division of the Mongol Empire and as an...
China became suspicious of knowledge it used. The Ming Dynasty
Ming Dynasty
The Ming Dynasty, also Empire of the Great Ming, was the ruling dynasty of China from 1368 to 1644, following the collapse of the Mongol-led Yuan Dynasty. The Ming, "one of the greatest eras of orderly government and social stability in human history", was the last dynasty in China ruled by ethnic...
turned away from math and physics in favor of botany
Botany
Botany, plant science, or plant biology is a branch of biology that involves the scientific study of plant life. Traditionally, botany also included the study of fungi, algae and viruses...
and pharmacology
Pharmacology
Pharmacology is the branch of medicine and biology concerned with the study of drug action. More specifically, it is the study of the interactions that occur between a living organism and chemicals that affect normal or abnormal biochemical function...
.
At this period, the abacus
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
which first appeared in Song dynasty now overtook the counting rods and became the preferred computing device. Zhu Zaiyu, Prince of Zheng who invented the equal temperament
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
used 81 position abacus to calculate the square root and cubic root of 2 to 25 figure accuracy.
However, this switching from counting rods to abacus to gain speed in calculation was at a high cost, causing the stagnation and decline of
Chinese mathematics. The pattern rich layout of counting rod numerals on counting board inspired many Chinese inventions in mathematics,such
as cross multiply principe of fractions, method for solving linear equations. The pattern rich counting rods inspired Japanese mathematician
to invent the concept of matrix. In Ming dynasty, mathematicians were fascinated with perfecting algorithms for abacus, many mathematical works
devoted to abacus mathematics appeared in this period, at the expense of new ideas creation.
Despite the achievements of Shen and Guo's work in trigonometry, another substantial work in Chinese trigonometry would not be published again until 1607, with the dual publication of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
by Chinese official and astronomer Xu Guangqi
Xu Guangqi
Xu Guangqi , was a Chinese scholar-bureaucrat, agricultural scientist, astronomer, and mathematician in the Ming Dynasty. Xu was a colleague and collaborator of the Italian Jesuits Matteo Ricci and Sabatino de Ursis and they translated several classic Western texts into Chinese, including part of...
(1562–1633) and the Italian Jesuit Matteo Ricci
Matteo Ricci
Matteo Ricci, SJ was an Italian Jesuit priest, and one of the founding figures of the Jesuit China Mission, as it existed in the 17th-18th centuries. His current title is Servant of God....
(1552–1610).
A revival of math in China began in the late nineteenth century, Joseph Edkins
Joseph Edkins
Joseph Edkins was a British Protestant missionary who spent 57 years in China, 30 of them in Beijing. As a Sinologue, he specialized in Chinese religions. He was also a linguist, a translator, and a philologist. Writing prolifically, he penned many books about the Chinese language and the Chinese...
, Alexander Wylie and Li Shanlan
Li Shanlan
Li Shanlan was a Chinese mathematician of the Qing Dynasty.A native of Haining, Zhejiang, he was fascinated by mathematics since childhood, beginning with the Nine Chapters on the Mathematical Art. He eked out a living by being a private tutor for some years before fleeing to Shanghai in 1852 to...
translated works on astronomy, algebra and differential-integral calculus into Chinese, published by London Missionary Press in Shanghai.
Mathematical texts
Zhou DynastyZhoubi Suanjing" c. 1000 BCE-100 CE
-Astronomical theories, and computation techniques
-Proof of the Pythagorean theorem (Shang Gao Theorem)
-Fractional computations
-Pythagorean theorem for astronomical purposes
Nine Chapters of Mathematical Arts1000 BCE? – 50 CE
-ch.1, computational algorithm, area of plane figures, GCF, LCD
-ch.2, proportions
-ch.3, proportions
-ch.4, square, cube roots, finding unknowns
-ch.5, volume and usage of pi as 3
-ch.6, proportions
-ch,7, interdeterminate equations
-ch.8, Gaussian elimination and matrices
-ch.9, Pythagorean theorem (Gougu Theorem)
See also
- Chinese astronomyChinese astronomyAstronomy in China has a very long history, with historians considering that "they [the Chinese] were the most persistent and accurate observers of celestial phenomena anywhere in the world before the Arabs."...
- History of mathematicsHistory of mathematicsThe area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
- Indian mathematicsIndian mathematicsIndian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
- Islamic mathematicsIslamic mathematicsIn the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
- Japanese mathematicsJapanese mathematicsdenotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
- Indian mathematics
External links
- Early mathematics texts (Chinese) - Chinese Text ProjectChinese Text ProjectThe Chinese Text Project is a digital library project that assembles collections of early Chinese texts. The name of the project in Chinese literally means "The Digitization Project of Chinese Philosophy Books", showing its focus on books related to Chinese philosophy...
- Overview of Chinese mathematics
- Chinese Mathematics Through the Han Dynasty