Wavefunction
Encyclopedia
Not to be confused with the related concept of the Wave equation
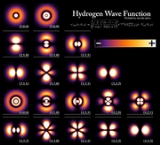
A wave function or wavefunction is a probability amplitude in quantum mechanics
describing the quantum state of a particle and how it behaves. Typically, its values are complex number
s and, for a single particle, it is a function
of space and time. The laws of quantum mechanics (the Schrödinger equation
) describe how the wave function evolves over time. The wave function behaves qualitatively like other wave
s, like water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation
. This explains the name "wave function", and gives rise to wave-particle duality.
The most common symbols for a wave function are ψ or Ψ (lower-case and capital psi
).
Although ψ is a complex number, |ψ|2 is real, and corresponds to the probability density
of finding a particle in a given place at a given time, if the particle's position is measured
.
The SI units for ψ depend on the system. For one particle in three dimensions, its units are m–3/2. These unusual units are required so that an integral of |ψ|2 over a region of three-dimensional space is a unitless probability (i.e., the probability that the particle is in that region). For different numbers of particles and/or dimensions, the units may be different.
The wave function is absolutely central to quantum mechanics: it makes the subject what it is. Also; it is the source of the mysterious consequences and philosophical difficulties in what quantum mechanics means in nature, and even how nature itself behaves at the atomic scale and beyond - which continue in debate to this day.
In the 1920s and 1930s, there were two divisions (so to speak) of theoretical physicists
who simultaneously founded quantum mechanics: one for calculus
and one for linear algebra
. Those who used the techniques of calculus included Louis de Broglie, Erwin Schrödinger
, Paul Dirac
, Hermann Weyl
, Oskar Klein
, Walter Gordon
, Douglas Hartree
and Vladimir Fock
. This hand of quantum mechanics became known as "wave mechanics". Those who applied the methods of linear algebra included Werner Heisenberg
, Max Born
, Wolfgang Pauli
and John Slater
. This other hand of quantum mechanics came to be called "matrix mechanics". Schrödinger was one who subsequently showed that the two approaches were equivalent. In each case, the wavefunction was at the centre of attention in two forms, giving quantum mechanics its ubiquitous unity.
Introduction of wave functions
De Broglie could be considered the founder of the wave model in 1925, due to his symmetric relation
between momentum
and wavelength
: the De Broglie equation. Schrödinger searched for an equation that would describe these waves, and was the first to construct and publish an equation for which the wave function satisfied in 1926, based on classical
energy
conservation
. Indeed it is now called the Schrödinger equation.
Interpretation and acceptance
However, no-one, even Schrödinger and De Broglie, were clear on how to interpret it. What did this function mean? Around 1924–27, Born, Heisenberg, Bohr and others provided the perspective of probability amplitude
. This is the Copenhagen interpretation
of quantum mechanics. There are many other interpretations of quantum mechanics, but this is considered the most important - since quantum calculations can be understood.
Applications and approximations
In 1927, Hartree and Fock made the first step in an attempt to solve the N-body
wave function, and developed the self-consistency cycle: an iterative
algorithm
to approximate the solution. Now it is also known as the Hartree–Fock method. The Slater
determinant
and permanent
(of a matrix
) was part of the method, provided by Slater.
Relativistic wave functions
Interestingly, Schrödinger did encounter an equation for which the wave function satisfied relativistic energy conservation before he published the non-relativistic one, but it lead to unacceptable consequences for that time so he discarded it. In 1927, Klien, Gorden and Fock also found it, but taking a step further: enmeshed the electromagnetic
interaction
into it and proved it was Lorentz-invariant
. De Broglie also arrived at exactly the same equation in 1928. This wave equation is now known most commonly as the Klein–Gordon equation .
By 1928 Dirac deduced his equation from the first successful unified combination of special relativity
and quantum mechanics to the electron
- the Dirac equation
. He found an unusual character of the wavefunction for this equation: it was not a single complex number, but a spinor
. Spin
automatically entered into the properties of the wavefunction. Although there were problems; Dirac was capable of resolving them. Around the same time Weyl also found his relativistic equation, which also had spinor solutions.
Later other wave equations were developed: see Relativistic wave equations
for further information.
and analysis
(study of functions
, change etc.) can be used to represent
the wavefunction in a number of situations. Superficially, this formalism is simple to understand for the following reasons.
Although these functions are continuous
- they are not deterministic; but probability distribution
s. Perhaps oddly; this approach is not the most general way to represent probability amplitudes. The more advanced techniques use linear algebra
(the study of vectors, matrices, etc.) and more generally still; abstract algebra
(algebraic structures, generalizations of Euclidean spaces etc.).
, in one spatial dimension. (More general cases are discussed below). The state of such a particle is completely described by its wave function:
,
where x is position and t is time. This function is complex-valued
, meaning that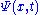
is a complex number
.
If the particle's position is measured
, its location is not deterministic, but is described by a probability distribution
. The probability that its position x will be in the interval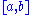
(meaning a ≤ x ≤ b) is: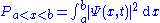
where t is the time at which the particle was measured. In other words,
is the probability density
that the particle is at x, rather than some other location.
This leads to the normalization condition: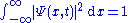
,
because if the particle is measured, there is 100% probability that it will be somewhere.
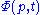
where p is the momentum
in one dimension, which can be any value from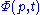
to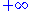 
, and t is time. If the particle's momentum is measured
, the result is not deterministic, but is described by a probability distribution: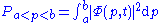
,
analogous to the position case. The position-space and momentum-space wave functions are Fourier transform
s of each other, therefore both contain the same information, and either one alone is sufficient to calculate any property of the particle. For one-dimension: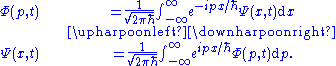
Sometimes the wave-vector k is used in place of momentum
p, since they are related by the de Broglie relation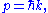
and the equivalent space is referred to as k-space. Again it makes no difference which is used since p and k are equivalent - up to a constant. In practice, the position-space wavefunction is used much more often than the momentum-space wavefunction.
. Specifically, the entire wave function is treated as a single abstract vector:
where
is a column vector written in bra-ket notation
. The statement that "wave functions form an abstract vector space" simply means that it is possible to add together different wave functions, and multiply wave functions by complex numbers (see vector space
for details). (Technically, because of the normalization condition, wave functions form a projective space
rather than an ordinary vector space.) This vector space is infinite-dimensional
, because there is no finite set of functions which can be added together in various combinations to create every possible function. Also, it is a Hilbert space
, because the inner product of wave functions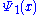
and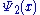 
can be defined as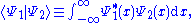
where * denotes complex conjugate
.
There are several advantages to understanding wave functions as elements of an abstract vector space:
H. Some properties of such a space are
Physically, the nature of the inner product is dependent on the basis in use, becuase the basis is chosen to reflect the quantum state of the system.
When the basis is a countable set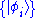
and orthonormal, that is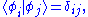
then an arbitrary vector
can be expressed as
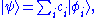
where the components are the (complex) numbers
This wave function is known as a descrete spectrum, since the bases are descrete.
When the basis is an uncountable set, the orthonormality condition holds similarly,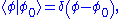
then an arbitrary vector
can be expressed as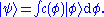
where the components are the functions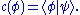
This wave function is known as a continuous spectrum, since the bases are continuous.
Paramount to the analysis is the Kronecker delta,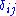
, and the Dirac delta function
,
, since the bases used are orthonormal. More detailed discussion of wave functions as elements of vector spaces is below, following further definitions.
,
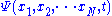The probability that particle 1 is in an x-interval R1 = [a1,b1] and particle 2 in interval R2 = [a2,b2] etc, up to particle N in interval RN = [aN,bN], all measured simultaneously at time t, is given by:
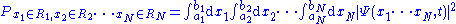
The normalization condition becomes:
.
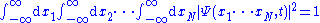In each case, there are N one-dimensional integrals, one for each particle.
The position-space wave function of a single particle in three spatial dimensions is similar to the case of one spatial dimension above:
where r is the position in three-dimensional space (r is short for (x,y,z)), and t is time. As always
is a complex number
. If the particle's position is measured at time t, the probability that it is in a region R is: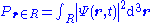
(a three-dimensional integral over the region R, with differential volume element d3r, also written "dV" or "dx dy dz"). The normalization condition is: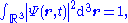
where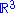
is all of three-dimensional space.
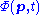
where p is the momentum in 3-dimensional space, and t is time. This time there are three components of momentum which can have values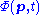
to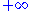 
in each direction, in Cartesian coordinates x, y, z.
The probability of measuring the momentum components px between a and b, py between c and d, and pz between e and f, is given by:
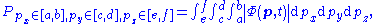
hence the normalization:
analogous to space, d3p = dpxdpydpz. The generalization of the previous Fourier transform is
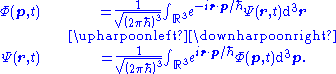
and the EPR paradox
possible. The position-space wave function for N particles is written:
where ri is the position of the ith particle in three-dimensional space, and t is time. If the particles' positions are all measured simultaneously at time t, the probability that particle 1 is in region R1 and particle 2 is in region R2 and so on is: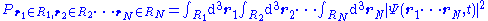
The normalization condition is: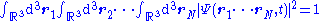
(altogether, this is 3N one-dimensional integrals).
In quantum mechanics there is a fundamental distinction between identical particles and distinguishable particles. For example, any two electrons are fundamentally indistinguishable from each other; the laws of physics make it impossible to "stamp an identification number" on a certain electron to keep track of it. This translates to a requirement on the wavefunction: For example, if particles 1 and 2 are indistinguishable, then: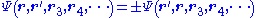
where the + sign is required if the particles are boson
s, and the – sign is required if they are fermion
s. More exactly stated:
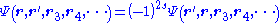
where s = spin quantum number,
The wavefunction is said to be symmetric (no sign change) under boson interchange and antisymmetric (sign changes) under fermion interchange.
, the wave function can be written in "position-spin-space" as: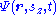
where r is a position in three-dimensional space, t is time, and sz is the spin projection quantum number
along the z axis. (The z axis is an arbitrary choice; other axes can be used instead if the wave function is transformed appropriately, see below.) The sz parameter, unlike r and t, is a discrete variable. For example, for a spin-1/2 particle, sz can only be +1/2 or -1/2, and not any other value. (In general, for spin s, sz can be s, s–1,...,–s.) If the particle's position and spin is measured simultaneously at time t, the probability that its position is in R1 and its spin projection quantum number is a certain value m is: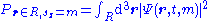
The normalization condition is: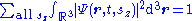
.
where
is all of three-dimensional space. Since the spin quantum number has discrete values, it must be written as a sum rather than an integral, taken over all possible values.
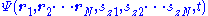
The probability that particle 1 is in region R1 with spin sz1 = m1 and particle 2 is in region R2 with spin sz2 = m2 etc reads (probability subscripts now removed due to their great length):
The normalization condition is:
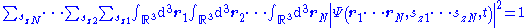
Now there are 3N one-dimensional integrals followed by N sums.
Hilbert space
). For the wave functions above, the Hilbert space usually has not only infinite dimensions, but uncountably infinitely many dimensions. On the hand, linear algebra
is much simpler for finite-dimensional vector spaces. Therefore it is helpful to look at an example where the Hilbert space of wave functions is finite dimensional.
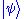, by expanding it in terms of other possible states of the same system - collectively referred to as a basis or representation 
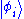. In what follows, all wave functions are assumed to be normalized.
An element of a vector space
can be expressed in different bases elements
; and so the same applies to wave functions. The components of a wave function describing the same physical state take different complex
values depending on the basis being used; however, just like elements of a vector space, the wave function itself is independent on the basis chosen. Choosing a new coordinate system does not change the vector itself, only the representation of the vector with respect to the new coordinate frame, since the components will be different but the linear combination of them still equals the vector.
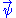with n components describes how to express the state of the physical system 
as the linear combination
of n basis elements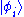
, (i = 1, 2...n). The following is a breakdown of the used formalism.
As a column vector or column matrix:
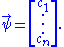
State vector: Ψ and bra-ket notation
Equivalently in bra-ket notation, the state of a particle with wave function Ψ can be written as a ket;
The corresponding bra is the complex conjugate of the transposed matrix (into a row matrix/row vector):
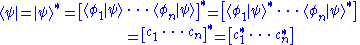
By "the state of a particle with wavefunction Ψ", written as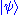
, this means the variables which characterize the system, with respect to the wavefunction. The wave function associated with a particular state may be seen as an expansion of the state in a basis of 
. For example, a basis could be for a free particle travelling in one dimension, with momentum eigenstates ψ± corresponding to the ±x direction:
Another example is the superposition of two energy eigenstates for a particle trapped in a 1-d box (these states are stationary state
):
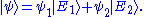
The most characteristic example is a particle in a spin up or down configuration:
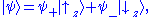
(see below for details of this frequent case). Notice how kets are not completely analogous to the ordinary notion of vectors - rather they are labels for a state of a wavefunction, which are used in a similar way. In all of the above examples, the particle is not in any one definite or preferred state, but rather in both at the same time - hence the term superposition. The free particle could be have momentum in the +x or –x direction simultaneously, the trapped particle in the 1-d potential well can be in the energy eigenstates corresponding to eigenvalues E1 and E2 at the same time, the particle with spin could be in spin up or down orientation at any instant of time. The relative chance of which state occurs is related to the (moduli squares of the) coefficients.
Ket Ψ, ket bases, and orthonormality
The choice of basis vectors is important, as two column vectors with the same components can represent two different states of a system if their associated basis states are different.
To illustrate this, let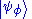
have the bases 
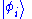and let 
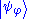have bases 
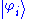, i.e.
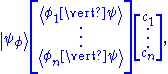
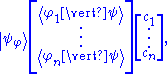
which implies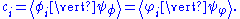
If for each index i;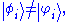
it then follows
The orthonormality relation is:
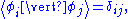
Ket Ψ and its components, the collapse postulate
The physical meaning of the components of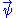
is given by the wave function collapse postulate:
The sum of the probabilities of all possible states must sum to 1 (see normalization using kets below), demanding:
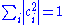
Each row or column matrix entry corresponds to a coefficient (of a ket) in the linear combination. The equality
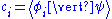
can be verified using the orthonormality relation,
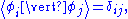
which allows any component to be found simply by multiplying by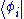
. For component q (between 1 and n),
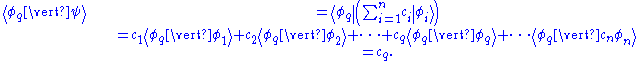
Ket Ψ and function Ψ
The wavefunction for position and momentum space, respectively, can be written using bra-ket notation in one dimension as:
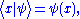
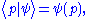
for three dimensions:
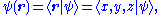
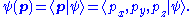
All read: the probability amplitude of a particle in state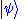
at position r or momentum p (in the relevant number of dimensions).
Note that (say)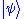
is not the same as 
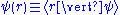. The former is the state of the particle, whereas the latter is simply a wave function describing how to express the former as a superposition of states with definite position.
Inner product of two ket vectors ψ and χ
Suppose we have another wavefunction in the same basis:
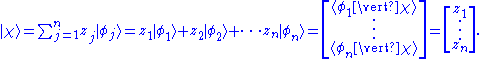
then the inner product can be defined as:
that is
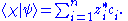
Outer product of two ket vectors ψ and χ and the closure relation
The outer product of two bra-ket vectors is defined as:
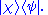
Summation over the inner product of like bases kets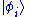
leads to the closure relation:
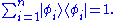
The equality to unity is not due to normalization, but because this is an identity operator (its action on anything leaves it unchanged). This can be used to obtain the ket wavefunction as a superposition of its basis vectors simply multiplying by the state of the wavefunction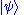
:
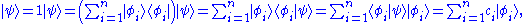
which was a previous statement. Also the inner product can be obtained:
Ket Ψ normalization
Starting from:
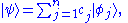
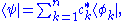
taking the inner product (and recalling orthonormality;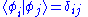
):
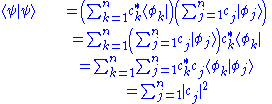
This expression means the projection of a complex probability amplitude onto itself is real. Since it is a probability amplitude, normalization requires this product to be unity, because it is equal to the sum of all possible quantum states (probabilities of these states occurring):
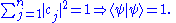
Collecting equivalences together:
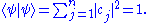
As a corollary, the normalization constant N can be written in terms of the coefficients of the vector components. Normally N is inserted into the eigenfunctions - then the normalizing sum of the squares of eiegnfunctions is done. Since |ψ|2 is calculated, N2 factors out of the sum rather than N. Even if ψ is left non-normalized then N2 can be inserted in front of the sum, then setting this multiplied sum to 1 will normalize ψ. Either way - N satisfies:
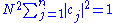
hence
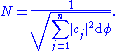
A normalizing constant scalar multiplies an non-normalized wavefunction ψ to obtain the normalized wavefunction ψ:
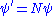
particle, but for this instance ignore its spatial degrees of freedom. Using the definition above, the wave function can now be written without position dependence:
,
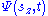where again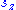
is the spin quantum number in the z-direction, either +1/2 or -1/2. So at a given time t, 
is completely characterized by just the two complex numbers Ψ(+1/2,t) and Ψ(–1/2,t). For simplicity these are often written as Ψ(+1/2,t) ≡ Ψ+ ≡ Ψ↑, and Ψ(–1/2,t) ≡ Ψ– ≡ Ψ↓ respectively. This is still called a "wave function", even though in this situation it has no resemblance to familiar wave
s (like mechanical wave
s), being only a pair of numbers instead of a continuous function.
Using the above formalism, the two numbers characterizing the wave function can be written as a column vector:
where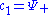
and 
. Therefore the set of all possible wave functions is a two dimensional complex vector space
. If the particle's spin projection in the z-direction is measured, it will be spin up (+1/2 ≡ ↑z) with probability
, and spin down (–1/2 ≡ ↓z) with probability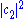 
.
In bra-ket notation
this can be written:
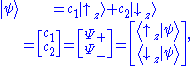
using the basis vectors (in alternate notations)
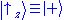for "spin up" or sz = +1/2,
for "spin down" or sz = –1/2.
The normalization requirement is
which says the probability of the particle in the spin up state (↑z, corresponding to the coefficient c1) plus the probability in the spin down(↓z, corresponding to the coefficient c2) state is 1.
To see this explicitly for this case, expand the ket in terms of the bases:
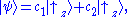
implying
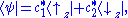
taking the inner product (and recalling orthonormality) leads to the normalization condition:
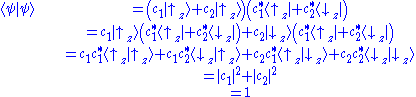
Conventional vector: Ψ and conventional notation
As a column vector or column matrix, there are infinitely many entries:
State vector: Ψ and bra-ket notation
In bra-ket notation;
The corresponding bra is as before:
. For this reason the collection of all states 
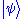is known as a continuum or spectrum of states. Finite or countably infinite basis vectors are summed over a discrete index - for a continuous basis the integral is over the continuous index, replacing the sum.
Continuously indexed vector: Ψ and bra-ket notation
As usual
is the physical state of the particle. The sum for a superposition of states now becomes an integral. In what follows, all integrals are with respect to the basis variable ϕ, over the required range. Usually this is just the real line or subset intervals of it. The state 
is given by:
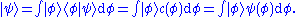
See below for more on notation of basis and components.
Ket Ψ, ket bases and orthonormality
As with the discrete bases, some symbol is used to denotes the basis states, again written in the form
, so that 
is the span of all these basis states. The symbol usually corresponds to some property or observable, but for generality any letter may be used. The general state is written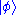 
, a particular state may be written as (say) subscripted or primed: 
or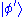 
. Alternatively and equivalently, 
denotes a basis ket for the state of ψ corresponding to the observable ϕ, the meaning is the same. In short the general basis can be written 
, and a particular basis is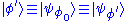 
.
The basis states are given by:
which can be deduced from the orthonormality and closure relations given below. The orthonormality relation is:
Ket Ψ and its components
The components of the state
are still 
, that is the projection of the wavefunction onto some basis is a component. This is a function of the basis variable ϕ, sometimes written using another symbol such as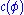 
or more usually the same as the physical state 
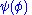, since the component of the state ψ corresponds to the basis ϕ. That is: 
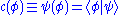. It is still true that 
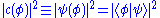is the probability density of measuring the observable ϕ. In what follows both alternatives are repeated to connect analogous notation with the previous summed countable states, and illustrate equivalence between notations used in the literature.
Inner product of two ket vectors ψ and χ
Given two states in the same basis:
the inner product becomes
that is
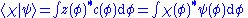
Outer product of two ket vectors ψ and χ and the closure relation
The outer product is still:
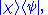
integrating over the inner product of like bases kets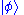
leads to the analogous closure relation:
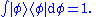
Multiplying by the state of the wavefunction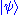
obtains the ket wavefunction as a superposition of its basis vectors:
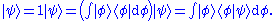
Also the inner product can be obtained:
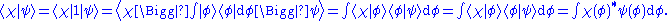
Ket Ψ normalization
Starting from:
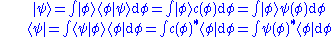
taking the inner product;
Since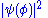
is the probability density of measuring the observable ϕ in the state ψ, this integral must be 1 as before:
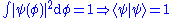
Collecting equivalences together:
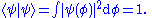
The normalization constant N for the continuous case can be manipulated in a similar way to the discrete case. The normalization constant N can be written in terms of the component continuum. Normally N is inserted into the eigenfunctions - then the normalizing integral of the squares of eiegnfunctions is done. Again |ψ|2 is calculated, and N2 factors out of the integrand rather than N. Even if ψ is left non-normalized then N2 can be inserted in front of the integral, then setting this multiplied integral to 1 will normalize ψ. Either way - N satisfies:
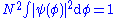
hence
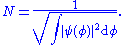
can be expanded in terms of a continuum of states with definite position, 
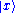, in the following way.
The basis states are the one-dimensional position states:
. Consider the region that the particle may occupy, given by the interval R = [a, b], then this implies the basis vectors are all the possible positions between x = a and x = b.
The components are:
.
Therefore the state for the wavefunction is:
In this case a base state can be expressed in terms of all possible basis states as:
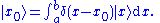
The spatial state of the wave function
associated with the position state 
is by orthogonality
.
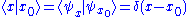We have the identity as another corollary of the closure relation, relating ψ(x) to a basis position x0;
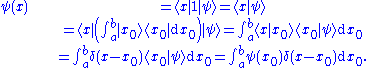
Taking the inner product of
with itself leads to the inner product stated at the beginning of this article (in that case 
and 
):
.
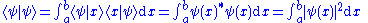For the inclusion of time dependance, simply attatch the time coordinate to all basis states by the replacements
However no integration with respect to t should be done becuase t is a constant; the instant x is measured to take some value in the interval a to b. For the momentum analogue, simply make the replacement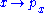
.
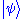can be expanded in terms of a continuum of states with definite position, 
as follows.
The basis states are the three-dimensional position states:
. Let the 3-dimensional region that the particle may occupy be R.
The components are:
.
Therefore the state for the wavefunction is:
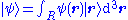
In this case a base state can be expressed in terms of all possible basis states as:
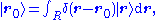
where the 3d Dirac-δ function is generalized to:
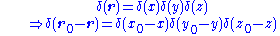
The spatial state of the wave function
associated with the position state 
is by orthogonally
.
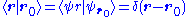Again we have the identity as another corollary of the closure relation, relating ψ(r) to a basis position r0;
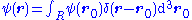
Taking the inner product of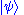
with itself leads to the normalization conditions in the three-dimensional definitions above:
.
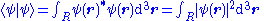In short, the above expressions take the same form for any number of spatial dimensions.
If these requirements are not met; it is not possible to interpret the wavefunction as a probability amplitude. The values of the wavefunction and its first order derivatives may not be finite and definite (exactly one value), i.e. probabilities can be infinite and multiple-valued at any one position and time - which is nonsense and doesn't satisfy the probability axioms
. Furthermore, when using the wavefunction to calculate a measurable observable of the quantum system, there will not be finite or definite values to calculate from - in this case the observable can take a number of values and can be infinite. This is unphysical and not observed when measuring in an experiment. Therefore a wavefunction is meaningful only if these conditions are satisfied.
valued quantity; only its relative phase and relative magnitude can be measured. It does not directly tell anything about the magnitudes or directions of measurable observables. An operator extracts this information by acting on the wavefunction ψ. For details and examples on how quantum mechanical operators act on the wave function, commutation of operators, and expectation values of operators; see Operator (physics).
. Many famous physicists of a previous generation puzzled over this problem, such as Schrödinger
, Einstein
and Bohr
. Some advocate formulations or variants of the Copenhagen interpretation
(e.g. Bohr, Wigner and von Neuman) while others, such as Wheeler
or Jaynes
, take the more classical approach and regard the wave function as representing information in the mind of the observer, i.e. a measure of our knowledge of reality. Some, ranging from Schrödinger, Einstein, Bohm
and Everett and others, argued that the wave function must have an objective, physical existence. For more on this topic, see Interpretations of quantum mechanics.
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
A wave function or wavefunction is a probability amplitude in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
describing the quantum state of a particle and how it behaves. Typically, its values are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and, for a single particle, it is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of space and time. The laws of quantum mechanics (the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
) describe how the wave function evolves over time. The wave function behaves qualitatively like other wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s, like water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. This explains the name "wave function", and gives rise to wave-particle duality.
The most common symbols for a wave function are ψ or Ψ (lower-case and capital psi
Psi (letter)
Psi is the 23rd letter of the Greek alphabet and has a numeric value of 700. In both Classical and Modern Greek, the letter indicates the combination /ps/ . The letter was adopted into the Old Italic alphabet, and its shape is continued into the Algiz rune of the Elder Futhark...
).
Although ψ is a complex number, |ψ|2 is real, and corresponds to the probability density
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of finding a particle in a given place at a given time, if the particle's position is measured
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
.
The SI units for ψ depend on the system. For one particle in three dimensions, its units are m–3/2. These unusual units are required so that an integral of |ψ|2 over a region of three-dimensional space is a unitless probability (i.e., the probability that the particle is in that region). For different numbers of particles and/or dimensions, the units may be different.
The wave function is absolutely central to quantum mechanics: it makes the subject what it is. Also; it is the source of the mysterious consequences and philosophical difficulties in what quantum mechanics means in nature, and even how nature itself behaves at the atomic scale and beyond - which continue in debate to this day.
Historical background
Calculus and linear algebra: wave and matrix mechanicsIn the 1920s and 1930s, there were two divisions (so to speak) of theoretical physicists
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
who simultaneously founded quantum mechanics: one for calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and one for linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. Those who used the techniques of calculus included Louis de Broglie, Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
, Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, Oskar Klein
Oskar Klein
Oskar Benjamin Klein was a Swedish theoretical physicist.Klein was born in Danderyd outside Stockholm, son of the chief rabbi of Stockholm, Dr. Gottlieb Klein from Homonna in Hungary and Antonie Levy...
, Walter Gordon
Walter Gordon
Walter Gordon may refer to:*Jamaa Fanaka, African-American filmmaker . He is sometimes credited as either Walt Gordon or Walter Gordon....
, Douglas Hartree
Douglas Hartree
Douglas Rayner Hartree PhD, FRS was an English mathematician and physicist most famous for the development of numerical analysis and its application to the Hartree-Fock equations of atomic physics and the construction of the meccano differential analyser.-Early life:Douglas Hartree was born in...
and Vladimir Fock
Vladimir Fock
Vladimir Aleksandrovich Fock was a Soviet physicist, who did foundational work on quantum mechanics and quantum electrodynamics....
. This hand of quantum mechanics became known as "wave mechanics". Those who applied the methods of linear algebra included Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
, Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
, Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
and John Slater
John Slater
John Slater may refer to:Business and government*John Fox Slater , American philanthropist, son of John Slater *John Slater , father of John Fox Slater, brother and partner of Samuel Slater...
. This other hand of quantum mechanics came to be called "matrix mechanics". Schrödinger was one who subsequently showed that the two approaches were equivalent. In each case, the wavefunction was at the centre of attention in two forms, giving quantum mechanics its ubiquitous unity.
Introduction of wave functions
De Broglie could be considered the founder of the wave model in 1925, due to his symmetric relation
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
between momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
and wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
: the De Broglie equation. Schrödinger searched for an equation that would describe these waves, and was the first to construct and publish an equation for which the wave function satisfied in 1926, based on classical
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
conservation
Conservation
Conservation may refer to:* Conservation movement, to protect animals, fungi, plants and their habitats** Conservation biology, the science of the protection and management of biodiversity...
. Indeed it is now called the Schrödinger equation.
Interpretation and acceptance
However, no-one, even Schrödinger and De Broglie, were clear on how to interpret it. What did this function mean? Around 1924–27, Born, Heisenberg, Bohr and others provided the perspective of probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
. This is the Copenhagen interpretation
Copenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
of quantum mechanics. There are many other interpretations of quantum mechanics, but this is considered the most important - since quantum calculations can be understood.
Applications and approximations
In 1927, Hartree and Fock made the first step in an attempt to solve the N-body
Many-body problem
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...
wave function, and developed the self-consistency cycle: an iterative
Iteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to approximate the solution. Now it is also known as the Hartree–Fock method. The Slater
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and permanent
Permanent
The permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
(of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
) was part of the method, provided by Slater.
Relativistic wave functions
Interestingly, Schrödinger did encounter an equation for which the wave function satisfied relativistic energy conservation before he published the non-relativistic one, but it lead to unacceptable consequences for that time so he discarded it. In 1927, Klien, Gorden and Fock also found it, but taking a step further: enmeshed the electromagnetic
Electromagnetic
Electromagnetic may refer to:* Electromagnetism* Electromagnetic field* Electromagnetic force* Electromagnetic radiation* Electromagnetic induction* Electromagnetic spectrum...
interaction
Interaction
Interaction is a kind of action that occurs as two or more objects have an effect upon one another. The idea of a two-way effect is essential in the concept of interaction, as opposed to a one-way causal effect...
into it and proved it was Lorentz-invariant
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
. De Broglie also arrived at exactly the same equation in 1928. This wave equation is now known most commonly as the Klein–Gordon equation .
By 1928 Dirac deduced his equation from the first successful unified combination of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and quantum mechanics to the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
- the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
. He found an unusual character of the wavefunction for this equation: it was not a single complex number, but a spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
. Spin
Spin
-In mathematics, science and technology:* Electron magnetic dipole moment* Rotation or spin, a movement of an object in a circular motion* Social Phobia Inventory, abbreviated as SPIN, a psychological test of social anxiety disorder....
automatically entered into the properties of the wavefunction. Although there were problems; Dirac was capable of resolving them. Around the same time Weyl also found his relativistic equation, which also had spinor solutions.
Later other wave equations were developed: see Relativistic wave equations
Relativistic wave equations
Before the creation of quantum field theory, physicists attempted to formulate versions of the Schrödinger equation which were compatible with special relativity...
for further information.
Wavefunctions as multi-variable functions - analytical calculus formalism
Multivariable calculusMultivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
and analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
(study of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, change etc.) can be used to represent
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
the wavefunction in a number of situations. Superficially, this formalism is simple to understand for the following reasons.
- It is more directly intiutive to have probability amplitudes as functions of space and time. At every position and time coordinate, the probability amplitude has a value by direct calculation.
- Functions can easily describe waveWaveIn physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
-like motion, using periodic functionPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s, and Fourier analysis can be readily done. - Functions are easy to produce, visualize and interpret, due to the pictorial nature of the graph of a functionGraph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
(i.e. curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s, contourContourContour may refer to:* an outline or silhouette* a contour line on a contour map, or the corresponding line on the ground or sea bed* Contour , a phonetic sound* Pitch contour , a melody shape...
s, surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s). When the situation is in a high number of dimensions (say 3) - it is possible to analyse the function in a lower dimensional slice (say 2) or contour plots of the function to determine the behaviour of the system within that confined region.
Although these functions are continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
- they are not deterministic; but probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. Perhaps oddly; this approach is not the most general way to represent probability amplitudes. The more advanced techniques use linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
(the study of vectors, matrices, etc.) and more generally still; abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
(algebraic structures, generalizations of Euclidean spaces etc.).
Position-space wavefunction
For now, consider the simple case of a single particle, without spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, in one spatial dimension. (More general cases are discussed below). The state of such a particle is completely described by its wave function:
,where x is position and t is time. This function is complex-valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, meaning that
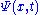is a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
.
If the particle's position is measured
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
, its location is not deterministic, but is described by a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. The probability that its position x will be in the interval
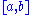(meaning a ≤ x ≤ b) is: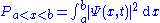where t is the time at which the particle was measured. In other words,
is the probability densityProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
that the particle is at x, rather than some other location.
This leads to the normalization condition:
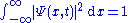,because if the particle is measured, there is 100% probability that it will be somewhere.
Momentum-space wavefunction
The particle also has a wave function in momentum space: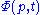where p is the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
in one dimension, which can be any value from
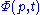to , and t is time. If the particle's momentum is measuredMeasurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
, the result is not deterministic, but is described by a probability distribution:
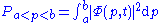,analogous to the position case. The position-space and momentum-space wave functions are Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s of each other, therefore both contain the same information, and either one alone is sufficient to calculate any property of the particle. For one-dimension:
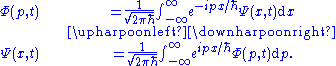
Sometimes the wave-vector k is used in place of momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
p, since they are related by the de Broglie relation
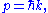
and the equivalent space is referred to as k-space. Again it makes no difference which is used since p and k are equivalent - up to a constant. In practice, the position-space wavefunction is used much more often than the momentum-space wavefunction.
Wave functions as an abstract vector space - linear/abstract algebra formalism
The set of all possible wave functions (at any given time) forms an abstract mathematical vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Specifically, the entire wave function is treated as a single abstract vector:
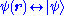
where
is a column vector written in bra-ket notationBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
. The statement that "wave functions form an abstract vector space" simply means that it is possible to add together different wave functions, and multiply wave functions by complex numbers (see vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
for details). (Technically, because of the normalization condition, wave functions form a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
rather than an ordinary vector space.) This vector space is infinite-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
, because there is no finite set of functions which can be added together in various combinations to create every possible function. Also, it is a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, because the inner product of wave functions
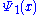and 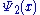can be defined as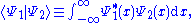where * denotes complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
.
There are several advantages to understanding wave functions as elements of an abstract vector space:
- All the powerful tools of linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
can be used to manipulate and understand wave functions. For example:- Linear algebra explains how a vector space can be given a basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, and then any vector can be expressed in this basis. This explains the relationship between a wave function in position space and a wave function in momentum space, and suggests that there are other possibilities too. - Bra-ket notationBra-ket notationBra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
can be used to manipulate wave functions.
- Linear algebra explains how a vector space can be given a basis
- The idea that quantum states are vectors in a Hilbert space is completely general in all aspects of quantum mechanics and quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, whereas the idea that quantum states are complex-valued "wave" functions of space is only true in certain situations.
Introduction to vector formalism
Given an isolated physical system, the allowed states of this system (i.e. the states the system could occupy without violating the laws of physics) are part of a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H. Some properties of such a space are
- If
and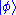 
are two allowed states, then 
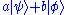is also an allowed state, provided 
. (This condition is due to normalisation, see below.) - There is always an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of allowed states of the vector space H.
Physically, the nature of the inner product is dependent on the basis in use, becuase the basis is chosen to reflect the quantum state of the system.
When the basis is a countable set
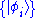and orthonormal, that is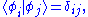then an arbitrary vector
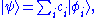
can be expressed aswhere the components are the (complex) numbers
This wave function is known as a descrete spectrum, since the bases are descrete.When the basis is an uncountable set, the orthonormality condition holds similarly,
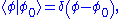
then an arbitrary vector
can be expressed as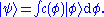where the components are the functions
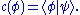This wave function is known as a continuous spectrum, since the bases are continuous.Paramount to the analysis is the Kronecker delta,
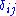, and the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
,
, since the bases used are orthonormal. More detailed discussion of wave functions as elements of vector spaces is below, following further definitions.Many spin-0 particles in one spatial dimension
The wavefunction can be generalized to incorporate N particles in one dimension: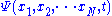,The probability that particle 1 is in an x-interval R1 = [a1,b1] and particle 2 in interval R2 = [a2,b2] etc, up to particle N in interval RN = [aN,bN], all measured simultaneously at time t, is given by:
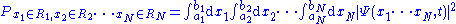
The normalization condition becomes:
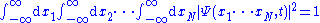.In each case, there are N one-dimensional integrals, one for each particle.
Position space wavefunction
where r is the position in three-dimensional space (r is short for (x,y,z)), and t is time. As always
is a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. If the particle's position is measured at time t, the probability that it is in a region R is:
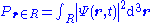
(a three-dimensional integral over the region R, with differential volume element d3r, also written "dV" or "dx dy dz"). The normalization condition is:
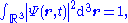
where
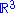is all of three-dimensional space.Momentum space wavefunction
There is a corresponding momentum space wavefunction for three-dimensions also: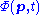where p is the momentum in 3-dimensional space, and t is time. This time there are three components of momentum which can have values
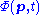to in each direction, in Cartesian coordinates x, y, z.The probability of measuring the momentum components px between a and b, py between c and d, and pz between e and f, is given by:
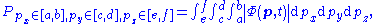
hence the normalization:
analogous to space, d3p = dpxdpydpz. The generalization of the previous Fourier transform is
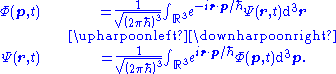
Many spin-0 particles in three spatial dimensions
When there are many particles, there is only one wave function, not a separate wave function for each particle. The fact that one wave function describes many particles is what makes quantum entanglementQuantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
and the EPR paradox
EPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
possible. The position-space wave function for N particles is written:
where ri is the position of the ith particle in three-dimensional space, and t is time. If the particles' positions are all measured simultaneously at time t, the probability that particle 1 is in region R1 and particle 2 is in region R2 and so on is:
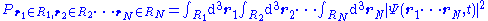
The normalization condition is:
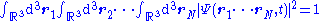
(altogether, this is 3N one-dimensional integrals).
In quantum mechanics there is a fundamental distinction between identical particles and distinguishable particles. For example, any two electrons are fundamentally indistinguishable from each other; the laws of physics make it impossible to "stamp an identification number" on a certain electron to keep track of it. This translates to a requirement on the wavefunction: For example, if particles 1 and 2 are indistinguishable, then:
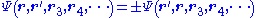
where the + sign is required if the particles are boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s, and the – sign is required if they are fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s. More exactly stated:
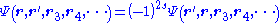
where s = spin quantum number,
- integer for bosons:
- and half-integer for fermions:
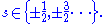
The wavefunction is said to be symmetric (no sign change) under boson interchange and antisymmetric (sign changes) under fermion interchange.
One particle with spin in three dimensions
For a particle with spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, the wave function can be written in "position-spin-space" as:
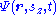
where r is a position in three-dimensional space, t is time, and sz is the spin projection quantum number
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
along the z axis. (The z axis is an arbitrary choice; other axes can be used instead if the wave function is transformed appropriately, see below.) The sz parameter, unlike r and t, is a discrete variable. For example, for a spin-1/2 particle, sz can only be +1/2 or -1/2, and not any other value. (In general, for spin s, sz can be s, s–1,...,–s.) If the particle's position and spin is measured simultaneously at time t, the probability that its position is in R1 and its spin projection quantum number is a certain value m is:
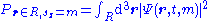
The normalization condition is:
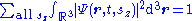.where
is all of three-dimensional space. Since the spin quantum number has discrete values, it must be written as a sum rather than an integral, taken over all possible values.Many particles with spin in three dimensions
Likewise, the wavefunction for N particles each with spin is: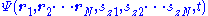The probability that particle 1 is in region R1 with spin sz1 = m1 and particle 2 is in region R2 with spin sz2 = m2 etc reads (probability subscripts now removed due to their great length):
The normalization condition is:
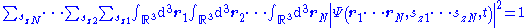
Now there are 3N one-dimensional integrals followed by N sums.
Wave functions in vector form
As explained above, quantum states are always vectors in an abstract vector space (technically, a complex projectiveProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
). For the wave functions above, the Hilbert space usually has not only infinite dimensions, but uncountably infinitely many dimensions. On the hand, linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
is much simpler for finite-dimensional vector spaces. Therefore it is helpful to look at an example where the Hilbert space of wave functions is finite dimensional.
Basis representation
A wave function describes the state of a physical system, by expanding it in terms of other possible states of the same system - collectively referred to as a basis or representation . In what follows, all wave functions are assumed to be normalized.An element of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
can be expressed in different bases elements
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
; and so the same applies to wave functions. The components of a wave function describing the same physical state take different complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
values depending on the basis being used; however, just like elements of a vector space, the wave function itself is independent on the basis chosen. Choosing a new coordinate system does not change the vector itself, only the representation of the vector with respect to the new coordinate frame, since the components will be different but the linear combination of them still equals the vector.
Finite dimensional basis vectors
To start, consider the finite basis representation. A wave function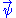 with n components describes how to express the state of the physical system as the linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of n basis elements
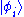, (i = 1, 2...n). The following is a breakdown of the used formalism.Formalism
Conventional vector: Ψ and conventional notationAs a column vector or column matrix:
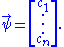
State vector: Ψ and bra-ket notation
Equivalently in bra-ket notation, the state of a particle with wave function Ψ can be written as a ket;
The corresponding bra is the complex conjugate of the transposed matrix (into a row matrix/row vector):
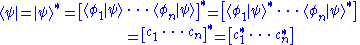
By "the state of a particle with wavefunction Ψ", written as
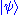, this means the variables which characterize the system, with respect to the wavefunction. The wave function associated with a particular state may be seen as an expansion of the state in a basis of . For example, a basis could be for a free particle travelling in one dimension, with momentum eigenstates ψ± corresponding to the ±x direction:Another example is the superposition of two energy eigenstates for a particle trapped in a 1-d box (these states are stationary state
Stationary state
In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
):
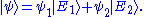
The most characteristic example is a particle in a spin up or down configuration:
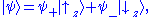
(see below for details of this frequent case). Notice how kets are not completely analogous to the ordinary notion of vectors - rather they are labels for a state of a wavefunction, which are used in a similar way. In all of the above examples, the particle is not in any one definite or preferred state, but rather in both at the same time - hence the term superposition. The free particle could be have momentum in the +x or –x direction simultaneously, the trapped particle in the 1-d potential well can be in the energy eigenstates corresponding to eigenvalues E1 and E2 at the same time, the particle with spin could be in spin up or down orientation at any instant of time. The relative chance of which state occurs is related to the (moduli squares of the) coefficients.
Ket Ψ, ket bases, and orthonormality
The choice of basis vectors is important, as two column vectors with the same components can represent two different states of a system if their associated basis states are different.
To illustrate this, let
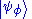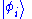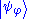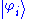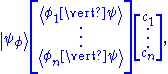
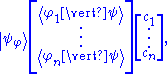
have the bases and let have bases , i.e.which implies
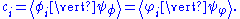
If for each index i;
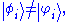
it then follows
The orthonormality relation is:
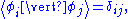
Ket Ψ and its components, the collapse postulate
The physical meaning of the components of
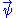is given by the wave function collapse postulate:The sum of the probabilities of all possible states must sum to 1 (see normalization using kets below), demanding:
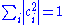
Each row or column matrix entry corresponds to a coefficient (of a ket) in the linear combination. The equality
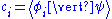
can be verified using the orthonormality relation,
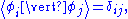
which allows any component to be found simply by multiplying by
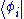. For component q (between 1 and n),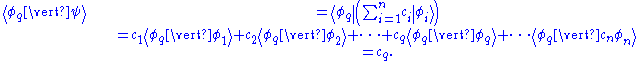Ket Ψ and function Ψ
The wavefunction for position and momentum space, respectively, can be written using bra-ket notation in one dimension as:
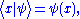
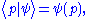
for three dimensions:
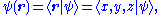
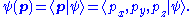
All read: the probability amplitude of a particle in state
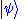at position r or momentum p (in the relevant number of dimensions).Note that (say)
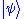is not the same as 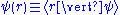. The former is the state of the particle, whereas the latter is simply a wave function describing how to express the former as a superposition of states with definite position.Inner product of two ket vectors ψ and χ
Suppose we have another wavefunction in the same basis:
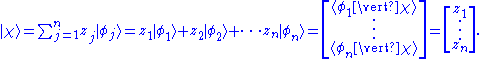
then the inner product can be defined as:
that is
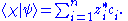
Outer product of two ket vectors ψ and χ and the closure relation
The outer product of two bra-ket vectors is defined as:
Summation over the inner product of like bases kets
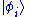leads to the closure relation: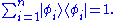The equality to unity is not due to normalization, but because this is an identity operator (its action on anything leaves it unchanged). This can be used to obtain the ket wavefunction as a superposition of its basis vectors simply multiplying by the state of the wavefunction
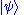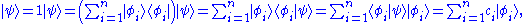
:which was a previous statement. Also the inner product can be obtained:
Ket Ψ normalization
Starting from:
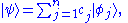
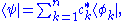
taking the inner product (and recalling orthonormality;
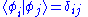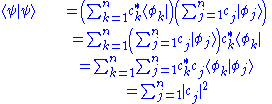
):This expression means the projection of a complex probability amplitude onto itself is real. Since it is a probability amplitude, normalization requires this product to be unity, because it is equal to the sum of all possible quantum states (probabilities of these states occurring):
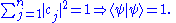
Collecting equivalences together:
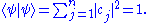
As a corollary, the normalization constant N can be written in terms of the coefficients of the vector components. Normally N is inserted into the eigenfunctions - then the normalizing sum of the squares of eiegnfunctions is done. Since |ψ|2 is calculated, N2 factors out of the sum rather than N. Even if ψ is left non-normalized then N2 can be inserted in front of the sum, then setting this multiplied sum to 1 will normalize ψ. Either way - N satisfies:
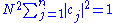
hence
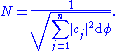
A normalizing constant scalar multiplies an non-normalized wavefunction ψ to obtain the normalized wavefunction ψ:
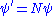
Application to one spin-½ particle (neglect spatial freedom)
A simple and important case is a spin-½Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
particle, but for this instance ignore its spatial degrees of freedom. Using the definition above, the wave function can now be written without position dependence:
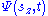,where again
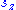is the spin quantum number in the z-direction, either +1/2 or -1/2. So at a given time t, is completely characterized by just the two complex numbers Ψ(+1/2,t) and Ψ(–1/2,t). For simplicity these are often written as Ψ(+1/2,t) ≡ Ψ+ ≡ Ψ↑, and Ψ(–1/2,t) ≡ Ψ– ≡ Ψ↓ respectively. This is still called a "wave function", even though in this situation it has no resemblance to familiar waveWave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s (like mechanical wave
Mechanical wave
A mechanical or material wave is a wave that needs a medium to travel. The oscillating material does not move far from its initial equilibrium position, as only the energy is transferred by connected particles. Ocean waves and sound are examples of this phenomenon.A mechanical wave requires an...
s), being only a pair of numbers instead of a continuous function.
Using the above formalism, the two numbers characterizing the wave function can be written as a column vector:
where
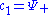and . Therefore the set of all possible wave functions is a two dimensional complex vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. If the particle's spin projection in the z-direction is measured, it will be spin up (+1/2 ≡ ↑z) with probability
, and spin down (–1/2 ≡ ↓z) with probability 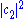.In bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
this can be written:
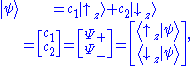
using the basis vectors (in alternate notations)
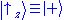for "spin up" or sz = +1/2, for "spin down" or sz = –1/2.The normalization requirement is
which says the probability of the particle in the spin up state (↑z, corresponding to the coefficient c1) plus the probability in the spin down(↓z, corresponding to the coefficient c2) state is 1.
To see this explicitly for this case, expand the ket in terms of the bases:
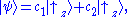
implying
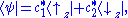
taking the inner product (and recalling orthonormality) leads to the normalization condition:
Infinite dimensional basis vectors
The case of a countably infinite vector, with a discrete index, is treated and interpreted in the same manner as a finite vector, except the sum is extended over an infinite number of basis elements.Conventional vector: Ψ and conventional notation
As a column vector or column matrix, there are infinitely many entries:
State vector: Ψ and bra-ket notation
In bra-ket notation;
The corresponding bra is as before:
Continuously indexed vectors
Now consider an uncountably infinite number of components of the physical state of the particle,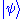. For this reason the collection of all states 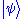is known as a continuum or spectrum of states. Finite or countably infinite basis vectors are summed over a discrete index - for a continuous basis the integral is over the continuous index, replacing the sum.Continuously indexed vector: Ψ and bra-ket notation
As usual
is the physical state of the particle. The sum for a superposition of states now becomes an integral. In what follows, all integrals are with respect to the basis variable ϕ, over the required range. Usually this is just the real line or subset intervals of it. The state is given by: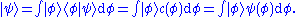See below for more on notation of basis and components.
Ket Ψ, ket bases and orthonormality
As with the discrete bases, some symbol is used to denotes the basis states, again written in the form
, so that is the span of all these basis states. The symbol usually corresponds to some property or observable, but for generality any letter may be used. The general state is written 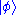, a particular state may be written as (say) subscripted or primed: or 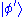. Alternatively and equivalently, denotes a basis ket for the state of ψ corresponding to the observable ϕ, the meaning is the same. In short the general basis can be written , and a particular basis is 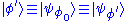.The basis states are given by:
which can be deduced from the orthonormality and closure relations given below. The orthonormality relation is:
Ket Ψ and its components
The components of the state
are still , that is the projection of the wavefunction onto some basis is a component. This is a function of the basis variable ϕ, sometimes written using another symbol such as 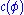or more usually the same as the physical state 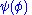, since the component of the state ψ corresponds to the basis ϕ. That is: 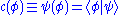. It is still true that 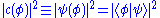is the probability density of measuring the observable ϕ. In what follows both alternatives are repeated to connect analogous notation with the previous summed countable states, and illustrate equivalence between notations used in the literature.Inner product of two ket vectors ψ and χ
Given two states in the same basis:
the inner product becomes
that is
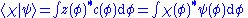
Outer product of two ket vectors ψ and χ and the closure relation
The outer product is still:
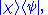
integrating over the inner product of like bases kets
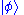leads to the analogous closure relation: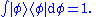Multiplying by the state of the wavefunction
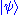obtains the ket wavefunction as a superposition of its basis vectors: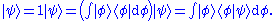Also the inner product can be obtained:
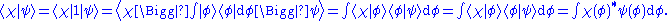
Ket Ψ normalization
Starting from:
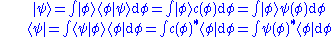
taking the inner product;
Since
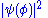is the probability density of measuring the observable ϕ in the state ψ, this integral must be 1 as before: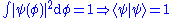Collecting equivalences together:
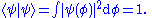
The normalization constant N for the continuous case can be manipulated in a similar way to the discrete case. The normalization constant N can be written in terms of the component continuum. Normally N is inserted into the eigenfunctions - then the normalizing integral of the squares of eiegnfunctions is done. Again |ψ|2 is calculated, and N2 factors out of the integrand rather than N. Even if ψ is left non-normalized then N2 can be inserted in front of the integral, then setting this multiplied integral to 1 will normalize ψ. Either way - N satisfies:
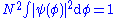
hence
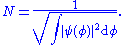
Application to one spin-0 particle in one spatial dimension
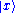An example of this is the spatial wave function of a particle. First consider one-dimension; the x-axis or real line (as in the one-dimensional cases above). Then can be expanded in terms of a continuum of states with definite position, , in the following way.The basis states are the one-dimensional position states:
. Consider the region that the particle may occupy, given by the interval R = [a, b], then this implies the basis vectors are all the possible positions between x = a and x = b.The components are:
.Therefore the state for the wavefunction is:
In this case a base state can be expressed in terms of all possible basis states as:
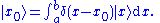
The spatial state of the wave function
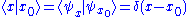associated with the position state is by orthogonality.We have the identity as another corollary of the closure relation, relating ψ(x) to a basis position x0;
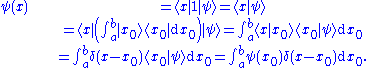
Taking the inner product of
with itself leads to the inner product stated at the beginning of this article (in that case and ):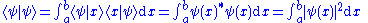.For the inclusion of time dependance, simply attatch the time coordinate to all basis states by the replacements
However no integration with respect to t should be done becuase t is a constant; the instant x is measured to take some value in the interval a to b. For the momentum analogue, simply make the replacement
.Application to one spin-0 particle in three spatial dimensions
The generalization of the previous result is straightforward. In three dimensions,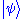 can be expanded in terms of a continuum of states with definite position, as follows.The basis states are the three-dimensional position states:
. Let the 3-dimensional region that the particle may occupy be R.The components are:
.Therefore the state for the wavefunction is:
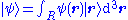
In this case a base state can be expressed in terms of all possible basis states as:
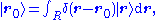
where the 3d Dirac-δ function is generalized to:
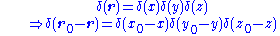
The spatial state of the wave function
associated with the position state is by orthogonally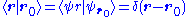.Again we have the identity as another corollary of the closure relation, relating ψ(r) to a basis position r0;
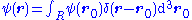
Taking the inner product of
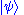with itself leads to the normalization conditions in the three-dimensional definitions above: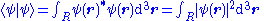.In short, the above expressions take the same form for any number of spatial dimensions.
Constraints
The wavefunction must satisfy the following requirements for the calculations and physical interpretation make sense:- It must everywhere be finite.
- It must everywhere be a continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, and continuously differentiableSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
(at least up to all possible first order derivatives).- As a corollary, the function would be single-valued, else multiple probabilities occur at the same position and time, again unphysical.
- It must everywhere satisfy the relavant normalization condition, so that the particle/system of particles exists somewhare with 100% certainty.
If these requirements are not met; it is not possible to interpret the wavefunction as a probability amplitude. The values of the wavefunction and its first order derivatives may not be finite and definite (exactly one value), i.e. probabilities can be infinite and multiple-valued at any one position and time - which is nonsense and doesn't satisfy the probability axioms
Probability axioms
In probability theory, the probability P of some event E, denoted P, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov, which are described below....
. Furthermore, when using the wavefunction to calculate a measurable observable of the quantum system, there will not be finite or definite values to calculate from - in this case the observable can take a number of values and can be infinite. This is unphysical and not observed when measuring in an experiment. Therefore a wavefunction is meaningful only if these conditions are satisfied.
Information about quantum systems
Although the wavefunction contains information, it is a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
valued quantity; only its relative phase and relative magnitude can be measured. It does not directly tell anything about the magnitudes or directions of measurable observables. An operator extracts this information by acting on the wavefunction ψ. For details and examples on how quantum mechanical operators act on the wave function, commutation of operators, and expectation values of operators; see Operator (physics).
Ontology
Whether the wave function really exists, and what it represents, are major questions in the interpretation of quantum mechanicsInterpretation of quantum mechanics
An interpretation of quantum mechanics is a set of statements which attempt to explain how quantum mechanics informs our understanding of nature. Although quantum mechanics has held up to rigorous and thorough experimental testing, many of these experiments are open to different interpretations...
. Many famous physicists of a previous generation puzzled over this problem, such as Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
, Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
and Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
. Some advocate formulations or variants of the Copenhagen interpretation
Copenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
(e.g. Bohr, Wigner and von Neuman) while others, such as Wheeler
John Archibald Wheeler
John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
or Jaynes
Edwin Thompson Jaynes
Edwin Thompson Jaynes was Wayman Crow Distinguished Professor of Physics at Washington University in St. Louis...
, take the more classical approach and regard the wave function as representing information in the mind of the observer, i.e. a measure of our knowledge of reality. Some, ranging from Schrödinger, Einstein, Bohm
David Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
and Everett and others, argued that the wave function must have an objective, physical existence. For more on this topic, see Interpretations of quantum mechanics.
Examples
Here are examples of wavefunctions for specific applications:- Free particleFree particleIn physics, a free particle is a particle that, in some sense, is not bound. In classical physics, this means the particle is present in a "field-free" space.-Classical Free Particle:The classical free particle is characterized simply by a fixed velocity...
- Particle in a boxParticle in a boxIn quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
- Finite square well
- Delta potential
- Quantum harmonic oscillatorQuantum harmonic oscillatorThe quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
- Hydrogen atom and Hydrogen-like atomHydrogen-like atomA hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
See also
- BosonBosonIn particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
- Double-slit experimentDouble-slit experimentThe double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
- Faraday waveFaraday waveFaraday waves, also known as Faraday ripples, named after Michael Faraday, are nonlinear standing waves that appear on liquids enclosed by a vibrating receptacle. When the vibration frequency exceeds a critical value, the flat hydrostatic surface becomes unstable. This is known as the Faraday...
- FermionFermionIn particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
- Normalisable wave function
- Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
- Wave function collapse
- Wave packetWave packetIn physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere...