.gif)
Basis (linear algebra)
Encyclopedia
In linear algebra
, a basis is a set of linearly independent
vector
s that, in a linear combination
, can represent every vector in a given vector space
or free module
, or, more simply put, which define a "coordinate system". In more general terms, a basis is a linearly independent spanning set.
Given a basis of vector space, every element of the vector space can be expressed uniquely as a finite linear combination of basis vectors. Every vector space has a basis, and all bases of a vector space have the same number of elements, called the dimension
of the vector space.
V over a field
F is a linearly independent
subset of V that span
s (or generates) V.
In more detail, suppose that B = { v1, …, vn } is a finite subset of a vector space V over a field
F (such as the real or complex number
s R or C). Then B is a basis if it satisfies the following conditions: for every x in V it is possible to choose a1, …, an ∈ F such that x = a1v1 + … + anvn.
The numbers ai are called the coordinates of the vector x with respect to the basis B, and by the first property they are uniquely determined.
A vector space that has a finite basis is called finite-dimensional
. To deal with infinite-dimensional spaces, we must generalize the above definition to include infinite basis sets. We therefore say that a set (finite or infinite) B ⊂ V is a basis, if for every x in V it is possible to choose a1, …, an ∈ F and v1, …, vn ∈ B such that x = a1v1 + … + anvn.
The sums in the above definition are all finite because without additional structure the axioms of a vector space
do not permit us to meaningfully speak about an infinite sum of vectors. Settings that permit infinite linear combinations allow alternative definitions of the basis concept: see Related notions below.
It is often convenient to list the basis vectors in a specific order, for example, when considering the transformation matrix of a linear map with respect to a basis. We then speak of an ordered basis, which we define to be a sequence
(rather than a set) of linearly independent vectors that span V: see Ordered bases and coordinates below.
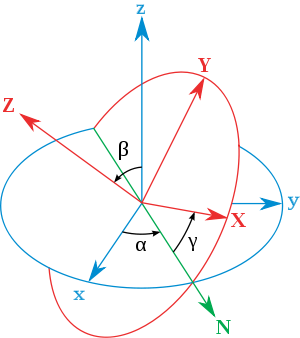 There are several ways to describe a basis for the space. Some are made ad-hoc for a specific dimension. For example, there are several ways
There are several ways to describe a basis for the space. Some are made ad-hoc for a specific dimension. For example, there are several ways
to give a basis in dim 3, like Euler angles
.
The general case is to give a matrix with the components of the new basis vectors in columns. This is also the more general method because it can express any possible set of vectors even if it is not a basis. This matrix can be seen as three things:
Basis Matrix: Is a matrix that represents the basis, because its columns are the components of vectors of the basis. This matrix represents any vector of the new basis as linear combination of the current basis.
Rotation operator: When orthonormal bases are used, any other orthonormal basis can be defined by a rotation matrix. This matrix represents the rotation operator that rotates the vectors of the basis to the new one. It is exactly the same matrix as before because the rotation matrix multiplied by the identity matrix I has to be the new basis matrix.
Change of basis matrix: This matrix can be used to change different objects of the space to the new basis. Therefore is called "change of basis
" matrix. It is important to note that some objects change their components with this matrix and some others, like vectors, with its inverse.
any of the following equivalent conditions are met:
Every vector space has a basis. The proof of this requires the axiom of choice. All bases of a vector space have the same cardinality
(number of elements), called the dimension
of the vector space. This result is known as the dimension theorem
, and requires the ultrafilter lemma, a strictly weaker form of the axiom of choice.
Also many vector sets can be attributed a standard basis
which comprises both spanning and linearly independent vectors.
Standard bases for example:
In Rn {E1,...,En} where En is the n-th column of the identity matrix which consists of all ones in the main diagonal and zeros everywhere else. This is because the columns of the identity matrix are linearly independent can always span a vector set by expressing it as a linear combination.
In P2 where P2 is the set of all polynomials of degree at most 2 {1,x,x2} is the standard basis.
In M22 {M1,1,M1,2,M2,1,M2,2} where M22 is the set of all 2x2 matrices. and Mm,n is the 2x2 matrix with a 1 in the m,n position and zeros everywhere else. This again is a standard basis since it is linearly independent and spanning.
A similar question is when does a subset S contain a basis. This occurs if and only if S spans V. In this case, S will usually contain several different bases.
Here, using three different proofs, we show that the vectors (1,1) and (−1,2) form a basis for R2.
Part I: If two vectors v,w are linearly independent, then (a and b scalars) implies
(a and b scalars) implies 
To prove that they are linearly independent, suppose that there are numbers a,b such that:
(i.e., they are linearly dependent) Then:
Subtracting the first equation from the second, we obtain:
Subtracting this equation from the first equation then:

Hence we have linear independence.
Part II: To prove that these two vectors generate R2, we have to let (a,b) be an arbitrary element of R2, and show that there exist numbers r,s ∈ R such that:

Then we have to solve the equations:


Subtracting the first equation from the second, we get:

Since the above matrix has a nonzero determinant, its columns form a basis of R2. See: invertible matrix.
a basis {vi} by the first n integers. An ordered basis is also called a frame.
Suppose V is an n-dimensional vector space over a field
F. A choice of an ordered basis for V is equivalent to a choice of a linear isomorphism φ from the coordinate space
Fn to V.
Proof. The proof makes use of the fact that the standard basis
of Fn is an ordered basis.
Suppose first that
is a linear isomorphism. Define an ordered basis {vi} for V by
where {ei} is the standard basis for Fn.
Conversely, given an ordered basis, consider the map defined by
where x = x1e1 + x2e2 + ... + xnen is an element of Fn. It is not hard to check that φ is a linear isomorphism.
These two constructions are clearly inverse to each other. Thus ordered bases for V are in 1-1 correspondence with linear isomorphisms Fn → V.
The inverse of the linear isomorphism φ determined by an ordered basis {vi} equips V with coordinates: if, for a vector v ∈ V, φ−1(v) = (a1, a2,...,an) ∈ Fn, then the components aj = aj(v) are the coordinates of v in the sense that v = a1(v) v1 + a2(v) v2 + ... + an(v) vn.
The maps sending a vector v to the components aj(v) are linear maps from V to F, because of φ−1 is linear. Hence they are linear functional
s. They form a basis for the dual space
of V, called the dual basis.
) or algebraic basis can be used to refer to a basis as defined in this article. This is to make a distinction with other notions of "basis" that exist when infinite-dimensional vector spaces are endowed with extra structure. The most important alternatives are orthogonal bases
on Hilbert space
s, Schauder bases
and Markushevich bases on normed linear spaces.
The common feature of the other notions is that they permit the taking of infinite linear combinations of the basic vectors in order to generate the space. This, of course, requires that infinite sums are meaningfully defined on these spaces, as is the case for topological vector space
s – a large class of vector spaces including e.g. Hilbert space
s, Banach space
s or Fréchet space
s.
The preference of other types of bases for infinite dimensional spaces is justified by the fact that the Hamel basis becomes "too big" in Banach spaces: If X is an infinite dimensional normed vector space which is complete
(i.e. X is a Banach space
), then any Hamel basis of X is necessarily uncountable. This is a consequence of the Baire category theorem
. The completeness as well as infinite dimension are crucial assumptions in the previous claim. Indeed, finite dimensional spaces have by definition finite basis and there are infinite dimensional (non-complete) normed spaces which have countable Hamel basis. Consider , the space of the sequence
, the space of the sequence
s of real numbers which have only finitely many non-zero coordinates, with the norm
of real numbers which have only finitely many non-zero coordinates, with the norm  The standard basis
The standard basis
is its countable Hamel basis.
, one learns that the functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are an "orthogonal basis" of the (real or complex) vector space of all (real or complex valued) functions on the interval [0, 2π] that are square-integrable on this interval, i.e., functions f satisfying

The functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are linearly independent, and every function f that is square-integrable on [0, 2π] is an "infinite linear combination" of them, in the sense that

for suitable (real or complex) coefficients ak, bk. But most square-integrable functions cannot be represented as finite linear combinations of these basis functions, which therefore do not comprise a Hamel basis. Every Hamel basis of this space is much bigger than this merely countably infinite set of functions. Hamel bases of spaces of this kind are typically not useful, whereas orthonormal bases of these spaces are essential in Fourier analysis.
, projective space
, convex set
, and cone
have related notions of (a basis for an n-dimensional affine space is points in general linear position), (essentially the same as an affine basis, this is
points in general linear position), (essentially the same as an affine basis, this is  points in general linear position, here in projective space), (the vertices of a polytope), and (points on the edges of a polygonal cone); see also a Hilbert basis (linear programming)
points in general linear position, here in projective space), (the vertices of a polytope), and (points on the edges of a polygonal cone); see also a Hilbert basis (linear programming)
.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a basis is a set of linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s that, in a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
, can represent every vector in a given vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
or free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
, or, more simply put, which define a "coordinate system". In more general terms, a basis is a linearly independent spanning set.
Given a basis of vector space, every element of the vector space can be expressed uniquely as a finite linear combination of basis vectors. Every vector space has a basis, and all bases of a vector space have the same number of elements, called the dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of the vector space.
Definition
A basis B of a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is a linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
subset of V that span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
s (or generates) V.
In more detail, suppose that B = { v1, …, vn } is a finite subset of a vector space V over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F (such as the real or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s R or C). Then B is a basis if it satisfies the following conditions:
- the
-
- for all
- the
The numbers ai are called the coordinates of the vector x with respect to the basis B, and by the first property they are uniquely determined.
A vector space that has a finite basis is called finite-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
. To deal with infinite-dimensional spaces, we must generalize the above definition to include infinite basis sets. We therefore say that a set (finite or infinite) B ⊂ V is a basis, if
- every finite subset
The sums in the above definition are all finite because without additional structure the axioms of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
do not permit us to meaningfully speak about an infinite sum of vectors. Settings that permit infinite linear combinations allow alternative definitions of the basis concept: see Related notions below.
It is often convenient to list the basis vectors in a specific order, for example, when considering the transformation matrix of a linear map with respect to a basis. We then speak of an ordered basis, which we define to be a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(rather than a set) of linearly independent vectors that span V: see Ordered bases and coordinates below.
Expression of a basis

Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
to give a basis in dim 3, like Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
.
The general case is to give a matrix with the components of the new basis vectors in columns. This is also the more general method because it can express any possible set of vectors even if it is not a basis. This matrix can be seen as three things:
Basis Matrix: Is a matrix that represents the basis, because its columns are the components of vectors of the basis. This matrix represents any vector of the new basis as linear combination of the current basis.
Rotation operator: When orthonormal bases are used, any other orthonormal basis can be defined by a rotation matrix. This matrix represents the rotation operator that rotates the vectors of the basis to the new one. It is exactly the same matrix as before because the rotation matrix multiplied by the identity matrix I has to be the new basis matrix.
Change of basis matrix: This matrix can be used to change different objects of the space to the new basis. Therefore is called "change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
" matrix. It is important to note that some objects change their components with this matrix and some others, like vectors, with its inverse.
Properties
Again, B denotes a subset of a vector space V. Then, B is a basis if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
any of the following equivalent conditions are met:
- B is a minimal generating set of V, i.e., it is a generating set and no proper subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of B is also a generating set. - B is a maximal set of linearly independent vectors, i.e., it is a linearly independent set but no other linearly independent set contains it as a proper subset.
- Every vector in V can be expressed as a linear combination of vectors in B in a unique way. If the basis is ordered (see Ordered bases and coordinates below) then the coefficients in this linear combination provide coordinates of the vector relative to the basis.
Every vector space has a basis. The proof of this requires the axiom of choice. All bases of a vector space have the same cardinality
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
(number of elements), called the dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of the vector space. This result is known as the dimension theorem
Dimension theorem for vector spaces
In mathematics, the dimension theorem for vector spaces states that all bases of a vector space have equally many elements. This number of elements may be finite, or given by an infinite cardinal number, and defines the dimension of the space....
, and requires the ultrafilter lemma, a strictly weaker form of the axiom of choice.
Also many vector sets can be attributed a standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
which comprises both spanning and linearly independent vectors.
Standard bases for example:
In Rn {E1,...,En} where En is the n-th column of the identity matrix which consists of all ones in the main diagonal and zeros everywhere else. This is because the columns of the identity matrix are linearly independent can always span a vector set by expressing it as a linear combination.
In P2 where P2 is the set of all polynomials of degree at most 2 {1,x,x2} is the standard basis.
In M22 {M1,1,M1,2,M2,1,M2,2} where M22 is the set of all 2x2 matrices. and Mm,n is the 2x2 matrix with a 1 in the m,n position and zeros everywhere else. This again is a standard basis since it is linearly independent and spanning.
Examples
- Consider R2, the vector space of all coordinates (a, b) where both a and b are real numbers. Then a very natural and simple basis is simply the vectors e1 = (1,0) and e2 = (0,1): suppose that v = (a, b) is a vector in R2, then v = a (1,0) + b (0,1). But any two linearly independent vectors, like (1,1) and (−1,2), will also form a basis of R2 (see the section Proving that a finite spanning set is a basis further down).
- More generally, the vectors e1, e2, ..., en are linearly independent and generate Rn. Therefore, they form a basis for Rn and the dimension of Rn is n. This basis is called the standard basisStandard basisIn mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
.
- Let V be the realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space generated by the functions et and e2t. These two functions are linearly independent, so they form a basis for V.
- Let R[x] denote the vector space of real polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s; then (1, x, x2, ...) is a basis of R[x]. The dimension of R[x] is therefore equal to aleph-0.
Extending to a basis
Let S be a subset of a vector space V. To extend S to a basis means to find a basis B that contains S as a subset. This can be done if and only if S is linearly independent. Almost always, there is more than one such B, except in rather special circumstances (i.e. L is already a basis, or L is empty and V has two elements).A similar question is when does a subset S contain a basis. This occurs if and only if S spans V. In this case, S will usually contain several different bases.
Example of alternative proofs
Often, a mathematical result can be proven in more than one way.Here, using three different proofs, we show that the vectors (1,1) and (−1,2) form a basis for R2.
From the definition of basis
We have to prove that these two vectors are linearly independent and that they generate R2.Part I: If two vectors v,w are linearly independent, then
 (a and b scalars) implies
(a and b scalars) implies 
To prove that they are linearly independent, suppose that there are numbers a,b such that:

(i.e., they are linearly dependent) Then:
- and and
Subtracting the first equation from the second, we obtain:
- so
Subtracting this equation from the first equation then:

Hence we have linear independence.
Part II: To prove that these two vectors generate R2, we have to let (a,b) be an arbitrary element of R2, and show that there exist numbers r,s ∈ R such that:

Then we have to solve the equations:


Subtracting the first equation from the second, we get:
- and then
- and finally

By the dimension theorem
Since (−1,2) is clearly not a multiple of (1,1) and since (1,1) is not the zero vector, these two vectors are linearly independent. Since the dimension of R2 is 2, the two vectors already form a basis of R2 without needing any extension.By the invertible matrix theorem
Simply compute the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

Since the above matrix has a nonzero determinant, its columns form a basis of R2. See: invertible matrix.
Ordered bases and coordinates
A basis is just a set of vectors with no given ordering. For many purposes it is convenient to work with an ordered basis. For example, when working with a coordinate representation of a vector it is customary to speak of the "first" or "second" coordinate, which makes sense only if an ordering is specified for the basis. For finite-dimensional vector spaces one typically indexesIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
a basis {vi} by the first n integers. An ordered basis is also called a frame.
Suppose V is an n-dimensional vector space over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. A choice of an ordered basis for V is equivalent to a choice of a linear isomorphism φ from the coordinate space
Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
Fn to V.
Proof. The proof makes use of the fact that the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
of Fn is an ordered basis.
Suppose first that
- φ : Fn → V
is a linear isomorphism. Define an ordered basis {vi} for V by
- vi = φ(ei) for 1 ≤ i ≤ n
where {ei} is the standard basis for Fn.
Conversely, given an ordered basis, consider the map defined by
- φ(x) = x1v1 + x2v2 + ... + xnvn,
where x = x1e1 + x2e2 + ... + xnen is an element of Fn. It is not hard to check that φ is a linear isomorphism.
These two constructions are clearly inverse to each other. Thus ordered bases for V are in 1-1 correspondence with linear isomorphisms Fn → V.
The inverse of the linear isomorphism φ determined by an ordered basis {vi} equips V with coordinates: if, for a vector v ∈ V, φ−1(v) = (a1, a2,...,an) ∈ Fn, then the components aj = aj(v) are the coordinates of v in the sense that v = a1(v) v1 + a2(v) v2 + ... + an(v) vn.
The maps sending a vector v to the components aj(v) are linear maps from V to F, because of φ−1 is linear. Hence they are linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s. They form a basis for the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of V, called the dual basis.
Analysis
In the context of infinite-dimensional vector spaces over the real or complex numbers, the term Hamel basis (named after Georg HamelGeorg Hamel
Georg Karl Wilhelm Hamel was a German mathematician with interests in mechanics, the foundations of mathematics and function theory....
) or algebraic basis can be used to refer to a basis as defined in this article. This is to make a distinction with other notions of "basis" that exist when infinite-dimensional vector spaces are endowed with extra structure. The most important alternatives are orthogonal bases
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, Schauder bases
Schauder basis
In mathematics, a Schauder basis or countable basis is similar to the usual basis of a vector space; the difference is that Hamel bases use linear combinations that are finite sums, while for Schauder bases they may be infinite sums...
and Markushevich bases on normed linear spaces.
The common feature of the other notions is that they permit the taking of infinite linear combinations of the basic vectors in order to generate the space. This, of course, requires that infinite sums are meaningfully defined on these spaces, as is the case for topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s – a large class of vector spaces including e.g. Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s or Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s.
The preference of other types of bases for infinite dimensional spaces is justified by the fact that the Hamel basis becomes "too big" in Banach spaces: If X is an infinite dimensional normed vector space which is complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
(i.e. X is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
), then any Hamel basis of X is necessarily uncountable. This is a consequence of the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
. The completeness as well as infinite dimension are crucial assumptions in the previous claim. Indeed, finite dimensional spaces have by definition finite basis and there are infinite dimensional (non-complete) normed spaces which have countable Hamel basis. Consider
 , the space of the sequence
, the space of the sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s
 of real numbers which have only finitely many non-zero coordinates, with the norm
of real numbers which have only finitely many non-zero coordinates, with the norm  The standard basis
The standard basisStandard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
is its countable Hamel basis.
Example
In the study of Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, one learns that the functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are an "orthogonal basis" of the (real or complex) vector space of all (real or complex valued) functions on the interval [0, 2π] that are square-integrable on this interval, i.e., functions f satisfying

The functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are linearly independent, and every function f that is square-integrable on [0, 2π] is an "infinite linear combination" of them, in the sense that

for suitable (real or complex) coefficients ak, bk. But most square-integrable functions cannot be represented as finite linear combinations of these basis functions, which therefore do not comprise a Hamel basis. Every Hamel basis of this space is much bigger than this merely countably infinite set of functions. Hamel bases of spaces of this kind are typically not useful, whereas orthonormal bases of these spaces are essential in Fourier analysis.
Affine geometry
The related notions of an affine spaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, and cone
Cone (linear algebra)
In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
have related notions of (a basis for an n-dimensional affine space is
 points in general linear position), (essentially the same as an affine basis, this is
points in general linear position), (essentially the same as an affine basis, this is  points in general linear position, here in projective space), (the vertices of a polytope), and (points on the edges of a polygonal cone); see also a Hilbert basis (linear programming)
points in general linear position, here in projective space), (the vertices of a polytope), and (points on the edges of a polygonal cone); see also a Hilbert basis (linear programming)Hilbert basis (linear programming)
In linear programming, a Hilbert basis for a convex cone C is an integer cone basis: minimal set of integer vectors such that every integer vector in C is a conical combination of the vectors in the Hilbert basis with integer coefficients....
.
Historical references
, reprint:External links
- Instructional videos from Khan Academy

