
Normalisable wavefunction
Encyclopedia
In quantum mechanics
, wave functions which describe real particle
s must be normalizable: the probability
of the particle to occupy any place must equal 1.
Mathematically
, in one dimension
this is expressed as:
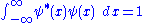
Or identically: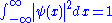
where the integration from to
to  indicates that the probability that the particle exists somewhere is unity.
indicates that the probability that the particle exists somewhere is unity.
All wave functions which represent real particles must be normalizable, that is, they must have a total probability of one - they must describe the probability of the particle existing as 100%. For certain boundary conditions, this trait enables anyone who solves the Schrödinger equation
to discard solutions which do not have a finite integral at a given interval. For example, this disqualifies periodic function
s as wave function solutions for infinite intervals, while those functions can be solutions for finite intervals.
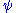 is a complex
is a complex
function
. However,
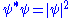
is real
, greater than or equal to zero, and is known as a probability density function
. Here, indicates the complex conjugate.
indicates the complex conjugate.
This means that
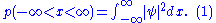
where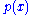 is the probability of finding the particle at
is the probability of finding the particle at  . Equation (1) is given by the definition of a probability density function
. Equation (1) is given by the definition of a probability density function
. Since the particle exists, its probability of being anywhere in space must be equal to 1. Therefore we integrate over all space:
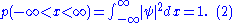
If the integral is finite, we can multiply the wave function,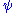 , by a constant such that the integral is equal to 1. Alternatively, if the wave function already contains an appropriate arbitrary constant, we can solve equation (2) to find the value of this constant which normalizes the wave function.
, by a constant such that the integral is equal to 1. Alternatively, if the wave function already contains an appropriate arbitrary constant, we can solve equation (2) to find the value of this constant which normalizes the wave function.
 and
and  ; its wave function is:
; its wave function is:
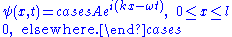
To normalize the wave function we need to find the value of the arbitrary constant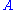 ; i.e., solve
; i.e., solve
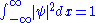
to find .
.
Substituting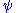 into
into 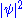 we get
we get
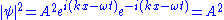
so,
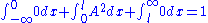
therefore;
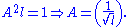
Hence, the normalized wave function is:

All properties of the particle such as: probability distribution, momentum, energy, expectation value of position etc.; are derived from the Schrödinger
wave equation. The properties are therefore unchanged if the Schrödinger wave equation is invariant under normalization.
The Schrödinger wave equation is:

If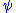 is normalized and replaced with
is normalized and replaced with 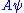 , then
, then
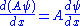 and
and 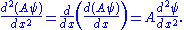
The Schrödinger wave equation therefore becomes:
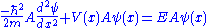
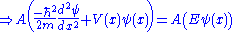
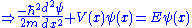
which is the original Schrödinger wave equation. That is to say, the Schrödinger wave equation is invariant
under normalization, and consequently associated properties are unchanged.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, wave functions which describe real particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s must be normalizable: the probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
of the particle to occupy any place must equal 1.
Mathematically
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in one dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
this is expressed as:
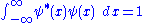
Or identically:
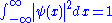
where the integration from
 to
to  indicates that the probability that the particle exists somewhere is unity.
indicates that the probability that the particle exists somewhere is unity.All wave functions which represent real particles must be normalizable, that is, they must have a total probability of one - they must describe the probability of the particle existing as 100%. For certain boundary conditions, this trait enables anyone who solves the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
to discard solutions which do not have a finite integral at a given interval. For example, this disqualifies periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s as wave function solutions for infinite intervals, while those functions can be solutions for finite intervals.
Derivation of normalization
In general,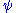 is a complex
is a complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. However,
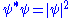
is real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, greater than or equal to zero, and is known as a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. Here,
 indicates the complex conjugate.
indicates the complex conjugate.This means that
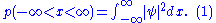
where
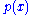 is the probability of finding the particle at
is the probability of finding the particle at  . Equation (1) is given by the definition of a probability density function
. Equation (1) is given by the definition of a probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. Since the particle exists, its probability of being anywhere in space must be equal to 1. Therefore we integrate over all space:
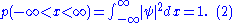
If the integral is finite, we can multiply the wave function,
 , by a constant such that the integral is equal to 1. Alternatively, if the wave function already contains an appropriate arbitrary constant, we can solve equation (2) to find the value of this constant which normalizes the wave function.
, by a constant such that the integral is equal to 1. Alternatively, if the wave function already contains an appropriate arbitrary constant, we can solve equation (2) to find the value of this constant which normalizes the wave function.Example of normalization
A particle is restricted to a 1D region between and
and  ; its wave function is:
; its wave function is: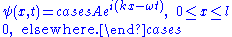
To normalize the wave function we need to find the value of the arbitrary constant
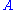 ; i.e., solve
; i.e., solve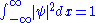
to find
 .
.Substituting
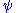 into
into 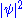 we get
we get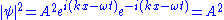
so,
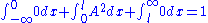
therefore;
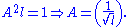
Hence, the normalized wave function is:

Proof that wave function normalization does not change associated properties
If normalization of a wave function changed the properties associated with the wave function, the process becomes pointless as we still cannot yield any information about the properties of the particle associated with the un-normalized wave function. It is therefore important to establish that the properties associated with the wave function are not altered by normalization.All properties of the particle such as: probability distribution, momentum, energy, expectation value of position etc.; are derived from the Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
wave equation. The properties are therefore unchanged if the Schrödinger wave equation is invariant under normalization.
The Schrödinger wave equation is:

If
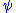 is normalized and replaced with
is normalized and replaced with 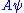 , then
, then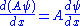 and
and 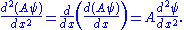
The Schrödinger wave equation therefore becomes:
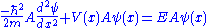
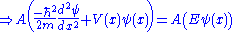
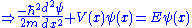
which is the original Schrödinger wave equation. That is to say, the Schrödinger wave equation is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under normalization, and consequently associated properties are unchanged.

