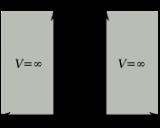
Particle in a box
Overview
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
and quantum systems. In classical systems, for example a ball trapped inside a heavy box, the particle can move at any speed within the box and it is no more likely to be found at one position than another.
Unanswered Questions

