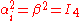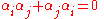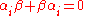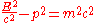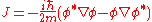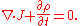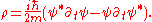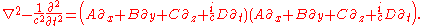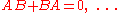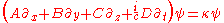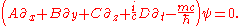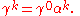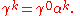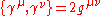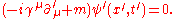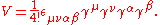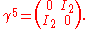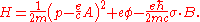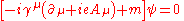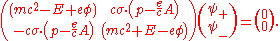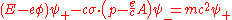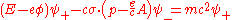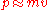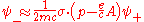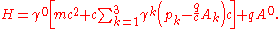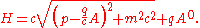Dirac equation
Encyclopedia
The Dirac equation is a relativistic
quantum mechanical
wave equation
formulated by British physicist Paul Dirac
in 1928. It provided a description of elementary
spin-½
particles, such as electron
s, consistent with both the principles of quantum mechanics and the theory of special relativity
, and was the first theory fully to account for relativity in the context of quantum mechanics. It accounted for the fine details of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, antimatter
, hitherto unsuspected and unobserved, and actually predated its experimental discovery. It also provided a theoretical justification for the introduction of several-component wave functions in Pauli's phenomenological theory of spin. Although Dirac did not at first fully appreciate what his own equation was telling him, his resolute faith in the logic of mathematics as a means to physical reasoning, his explanation of spin as a consequence of the union of quantum mechanics and relativity, and the eventual discovery of the positron, represents one of the great triumphs of theoretical physics, fully on a par with the work of Newton
, Maxwell
, and Einstein
before him.
Dirac's purpose in casting this equation was to explain the behavior of the relativistically moving electron, and so to allow the atom to be treated in a manner consistent with relativity. His rather modest hope was that the corrections introduced this way might have bearing on the problem of atomic spectra. Up until that time, attempts to make the old quantum theory of the atom compatible with the theory of relativity, attempts based on discretizing the angular momentum stored in the electron's possibly non-circular orbit of the atomic nucleus, had failed - and the new quantum mechanics of Heisenberg, Pauli, Jordan, Schrödinger, and Dirac himself had not developed sufficiently to treat this problem. Although Dirac's original intentions were satisfied, his equation had far deeper implications for the structure of matter, and introduced new mathematical classes of objects that are now essential elements of fundamental physics.
The new elements in this equation are the 4×4 matrices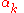
and 
, and the four-component wave function
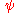. The matrices are all Hermitian and have squares equal to the 4 × 4 identity matrix
:
and they all mutually anticommute:
when i and j are distinct. The single symbolic equation thus unravels into four coupled linear first-order partial differential equations for the four quantities that make up the wave function. These matrices, and the form of the wave function, have a deep mathematical significance. The algebraic structure represented by the Dirac matrices had been created some 50 years earlier by the English mathematician W. K. Clifford
. In turn, Clifford's ideas had emerged from the mid-19th century work of the German mathematician Hermann Grassmann
in his "Lineale Ausdehnungslehre" (Theory of Linear Extensions). The latter had been regarded as well-nigh incomprehensible by most of his contemporaries. The appearance of something so seemingly abstract, at such a late date, and in such a direct physical manner, is one of the most remarkable chapters in the history of physics.
for a free massive particle:
The left side represents the square of the momentum operator divided by twice the mass, which is the non-relativistic kinetic energy. Because relativity treats space and time as a whole, a relativistic generalization of this equation requires that space and time derivatives must enter symmetrically, as they do in the Maxwell equations that govern the behavior of light — the equations must be differentially of the same order in space and time. In relativity, the momentum and the energy are the space and time parts of a space-time vector, the 4-momentum, and they are related by the relativistically invariant relation
which says that the length of this vector is proportional to the rest mass m. Substituting the operator equivalents of the energy and momentum from the Schrödinger theory, we get an equation describing the propagation of waves, constructed from relativistically invariant objects,
with the wave function
being a relativistic scalar: a complex number which has the same numerical value in all frames of reference. The space and time derivatives both enter to second order. This has a telling consequence for the interpretation of the equation. Because the equation is second order in the time derivative, then by the nature of solving differential equations, one must specify both the initial values of the wave function itself and of its first time derivative, in order to solve definite problems. Because both may be specified more or less arbitrarily, the wave function cannot maintain its former role of determining the probability density of finding the electron in a given state of motion. In the Schrödinger theory, the probability density is given by the positive definite expression
and this density is convected according to the probability current vector
with the conservation of probability current and density following from the Schrödinger equation:
The fact that the density is positive definite and convected according to this continuity equation, implies that we may integrate the density over a certain domain and set the total to 1, and this condition will be maintained by the conservation law. A proper relativistic theory with a probability density current must also share this feature. Now, if we wish to maintain the notion of a convected density, then we must generalize the Schrödinger expression of the density and current so that the space and time derivatives again enter symmetrically in relation to the scalar wave function. We are allowed to keep the Schrödinger expression for the current, but must replace by probability density by the symmetrically formed expression
which now becomes the 4th component of a space-time vector, and the entire 4-current density has the relativistically covariant expression
The continuity equation is as before. Everything is compatible with relativity now, but we see immediately that the expression for the density is no longer positive definite - the initial values of both
and 
may be freely chosen, and the density may thus become negative, something that is impossible for a legitimate probability density. Thus we cannot get a simple generalization of the Schrödinger equation under the naive assumption that the wave function is a relativistic scalar, and the equation it satisfies, second order in time.
Although it is not a successful relativistic generalization of the Schrödinger equation, this equation is resurrected in the context of quantum field theory, where it is known as the Klein–Gordon equation, and describes a spinless particle field (e.g. pi meson). Historically, Schrödinger himself arrived at this equation before the one that bears his name, but soon discarded it. In the context of quantum field theory, the indefinite density is understood to correspond to the charge density, which can be positive or negative, and not the probability density.
, replace p by its operator equivalent, expand the square root in an infinite series of derivative operators, set up an eigenvalue problem, then solve the equation formally by iterations. Most physicists had little faith in such a process, even if it were technically possible.
As the story goes, Dirac was staring into the fireplace at Cambridge, pondering this problem, when he hit upon the idea of taking the square root of the wave operator thus:
On multiplying out the right side we see that, in order to get all the cross-terms such as
to vanish, we must assume
with
Dirac, who had just then been intensely involved with working out the foundations of Heisenberg's matrix mechanics
, immediately understood that these conditions could be met if A, B, C and D are matrices, with the implication that the wave function has multiple components. This immediately explained the appearance of two-component wave functions in Pauli's phenomenological theory of spin
, something that up until then had been regarded as mysterious, even to Pauli himself. However, one needs at least 4×4 matrices to set up a system with the properties required — so the wave function had four components, not two, as in the Pauli theory, or one, as in the bare Schrödinger theory. The four-component wave function represents a new class of mathematical object in physical theories, spinor
s, that makes its first appearance here.
Given the factorization in terms of these matrices, one can now write down immediately an equation
with
to be determined. Applying again the matrix operator on both side yields
On taking
we find that all the components of the wave function individually satisfy the relativistic energy–momentum relation. Thus the sought-for equation that is first-order in both space and time is
Setting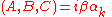
and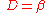 
, we get the Dirac equation as written above.
and the equation takes the form
In practice one often writes the gamma matrices in terms of 2x2 sub-matrices taken from the Pauli matrices
and the 2x2 identity matrix. Explicitly the standard representation is
The complete system is summarized using the Minkowski metric on spacetime in the form
where the bracket expression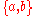
means 
, the anticommutator. These are the defining relations of a Clifford algebra
over a pseudo-orthogonal 4-d space with metric signature
. The specific Clifford algebra employed in the Dirac equation is known today as the Dirac algebra
. Although not recognized as such by Dirac at the time the equation was formulated, in hindsight the introduction of this geometric algebra represents an enormous stride forward in the development of quantum theory.
The Dirac equation may now be interpreted as an eigenvalue equation, where the rest mass is proportional to an eigenvalue of the 4-momentum operator, the proportion being the speed of light:
In practice, physicists often use units of measure such that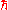
and c are equal to 1, known as "natural units
". The equation then takes the simple form
A fundamental theorem states that if two distinct sets of matrices are given that both satisfy the Clifford relations, then they are connected to each other by a similarity transformation:
If in addition the matrices are all unitary
, as are the Dirac set, then S itself is unitary;
The transformation U is unique up to a multiplicative factor of absolute value 1. Let us now imagine a Lorentz transformation to have been performed on the space and time coordinates, and on the derivative operators, which form a covariant vector. For the operator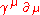
to remain invariant, the gammas must transform among themselves as a contravariant vector with respect to their spacetime index. These new gammas will themselves satisfy the Clifford relations, because of the orthogonality of the Lorentz transformation. By the fundamental theorem, we may replace the new set by the old set subject to a unitary transformation. In the new frame, remembering that the rest mass is a relativistic scalar, the Dirac equation will then take the form
If we now define the transformed spinor
then we have the transformed Dirac equation in a way that demonstrates manifest relativistic invariance:
Thus, once we settle on any unitary representation of the gammas, it is final provided we transform the spinor according the unitary transformation that corresponds to the given Lorentz transformation. The various representations of the Dirac matrices employed will bring into focus particular aspects of the physical content in the Dirac wave function (see below). The representation shown here is known as the standard representation - in it, the wave function's upper two components go over into Pauli's 2-spinor wave function in the limit of low energies and small velocities in comparison to light.
The considerations above reveal the origin of the gammas in geometry, hearkening back to Grassmann's original motivation - they represent a fixed basis of unit vectors in spacetime. Similarly, products of the gammas such as
represent oriented surface elements, and so on. With this in mind, we can find the form the unit volume element on spacetime in terms of the gammas as follows. By definition, it is
For this to be an invariant, the epsilon symbol must be a tensor, and so must contain a factor of
, where g is the determinant of the metric tensor. Since this is negative, that factor is imaginary. Thus
This matrix is given the special symbol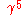
, owing to its importance when one is considering improper transformations of spacetime, that is, those that change the orientation of the basis vectors. In the standard representation it is
This matrix will also be found to anticommute with the other four Dirac matrices. It takes a leading role when questions of parity arise, because the volume element as a directed magnitude changes sign under a space-time reflection. Taking the positive square root above thus amounts to choosing a handedness convention on space-time.
where
is the conjugate transpose
of
, and noticing that
we obtain, by taking the Hermitian conjugate of the Dirac equation and multiplying from the right by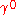
, the adjoint equation:
where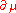
is understood to act to the left. Multiplying the Dirac equation by 
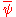from the left, and the adjoint equation by 
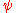from the right, and subtracting, produces the law of conservation of the Dirac current:
Now we see the great advantage of the first-order equation over the one Schrödinger had tried - this is the conserved current density required by relativistic invariance, only now its 4th component is positive definite and thus suitable for the role of a probability density:
Because the probability density now appears as the fourth component of a relativistic vector, and not a simple scalar as in the Schrödinger equation, it will be subject to the usual effects of the Lorentz transformations such as time dilation. Thus for example atomic processes that are observed as rates, will necessarily be adjusted in a way consistent with relativity, while those involving the measurement of energy and momentum, which themselves form a relativistic vector, will undergo parallel adjustment which preserves the relativistic covariance of the observed values.
goes back experimentally to the results of the Stern–Gerlach experiment
. A beam of atoms is run through a strong inhomogeneous magnetic field, which then splits into N parts depending on the intrinsic angular momentum of the atoms. It was found that for silver atoms, the beam was split in two—the ground state therefore could not be integral, because even if the intrinsic angular momentum of the atoms were as small as possible, 1, the beam would be split into 3 parts, corresponding to atoms with Lz = −1, 0, and +1. The conclusion is that silver atoms have net intrinsic angular momentum of . Pauli
set up a theory which explained this splitting by introducing a two-component wave function and a corresponding correction term in the Hamiltonian
, representing a semi-classical coupling of this wave function to an applied magnetic field, as so:
Here
and 
represent the electromagnetic field, and the three sigmas are the Pauli matrices. On squaring out the first term, a residual interaction with the magnetic field is found, along with the usual classical Hamiltonian of a charged particle interacting with an applied field:
This Hamiltonian is now a 2 × 2 matrix, so the Schrödinger equation based on it must use a two-component wave function. Pauli had introduced the 2x2 sigma matrices as pure phenomenology— Dirac now had a theoretical argument that implied that spin
was somehow the consequence of the marriage of quantum mechanics to relativity. On introducing the external electromagnetic 4-vector potential into the Dirac equation in a similar way, known as minimal coupling
, it takes the form (in natural units)
A second application of the Dirac operator will now reproduce the Pauli term exactly as before, because the spatial Dirac matrices multiplied by i, have the same squaring and commutation properties as the Pauli matrices. What is more, the value of the gyromagnetic ratio of the electron, standing in front of Pauli's new term, is explained from first principles. This was a major achievement of the Dirac equation and gave physicists great faith in its overall correctness. There is more however. The Pauli theory may be seen as the low energy limit of the Dirac theory in the following manner. First the equation is written in the form of coupled equations for 2-spinors with the units restored:
so
Assuming the field is weak and the motion of the electron non-relativistic, we have the total energy of the electron approximately equal to its rest energy, and the momentum going over to the classical value,
and so the second equation may be written
which is of order v/c - thus at typical energies and velocities, the bottom components of the Dirac spinor in the standard representation are much suppressed in comparison to the top components. Substituting this expression into the first equation gives after some rearrangement
The operator on the left represents the particle energy reduced by its rest energy, which is just the classical energy, so we recover Pauli's theory if we identify his 2-spinor with the top components of the Dirac spinor in the non-relativistic approximation. A further approximation gives the Schrödinger equation as the limit of the Pauli theory. Thus the Schrödinger equation may be seen as the far non-relativistic approximation of the Dirac equation when one may neglect spin and work only at low energies and velocities. This also was a great triumph for the new equation, as it traced the mysterious i that appears in it, and the necessity of a complex wave function, back to the geometry of space-time through the Dirac algebra. It also highlights why the Schrödinger equation, although superficially in the form of a diffusion equation, actually represents the propagation of waves.
It should be strongly emphasized that this separation of the Dirac spinor into large and small components depends explicitly on a low-energy approximation. The entire Dirac spinor represents an irreducible whole, and the components we have just neglected to arrive at the Pauli theory will bring in new phenomena in the relativistic regime - antimatter
and the idea of creation and annihilation of particles.
In a general case (if a certain linear function of electromagnetic field does not vanish identically), three out of four components of the spinor function in the Dirac equation can be algebraically eliminated, yielding an equivalent fourth-order partial differential equation for just one component. Furthermore, this remaining component can be made real by a gauge transform.
that enables to define Dirac matrices at every point. Contracting
these matrices with vierbeins give the right transformation properties. This way Dirac's equation takes the following form in curved spacetime:
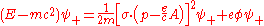
Here
is the vierbein and 
is the covariant derivative
for fermion fields, defined as follows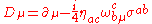
where
is the Lorentzian metric, 
is the commutator of Dirac matrices:
and
is the spin connection
:
where
is the Christoffel symbol. Note that here, Latin letters denote the "Lorentzian" indices and Greek ones denote "Riemannian" indices.
This looks promising, because we see by inspection the rest energy of the particle and, in case
, the energy of a charge placed in an electric potential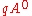 
. What about the term involving the vector potential? In classical electrodynamics, the energy of a charge moving in an applied potential is
Thus the Dirac Hamiltonian is fundamentally distinguished from its classical counterpart, and we must take great care to correctly identify what is an observable in this theory. Much of the apparent paradoxical behavior implied by the Dirac equation amounts to a misidentification of these observables. Let us now describe one such effect. (cont'd)
Klein paradox
: when a Dirac electron interacts with an electric potential, the total probability is not conserved.
Also, the electron can tunnel into high potential barriers, unlike the case in classical quantum mechanics described by the Schrödinger equation.
Zitterbewegung
: apparent fluctuation (at the speed of light) of the position of an electron around the median.
s. Real electrons obviously do not behave in this way.
To cope with this problem, Dirac introduced the hypothesis, known as hole theory, that the vacuum
is the many-body quantum state in which all the negative-energy electron eigenstates are occupied. This description of the vacuum as a "sea" of electrons is called the Dirac sea
. Since the Pauli exclusion principle
forbids electrons from occupying the same state, any additional electron would be forced to occupy a positive-energy eigenstate, and positive-energy electrons would be forbidden from decaying into negative-energy eigenstates.
Dirac further reasoned that if the negative-energy eigenstates are incompletely filled, each unoccupied eigenstate – called a hole – would behave like a positively charged particle. The hole possesses a positive energy, since energy is required to create a particle–hole pair from the vacuum. As noted above, Dirac initially thought that the hole might be the proton, but Hermann Weyl
pointed out that the hole should behave as if it had the same mass as an electron, whereas the proton is over 1800 times heavier. The hole was eventually identified as the positron
, experimentally discovered by Carl Anderson
in 1932.
It is not entirely satisfactory to describe the "vacuum" using an infinite sea of negative-energy electrons. The infinitely negative contributions from the sea of negative-energy electrons has to be canceled by an infinite positive "bare" energy and the contribution to the charge density and current coming from the sea of negative-energy electrons is exactly canceled by an infinite positive "jellium
" background so that the net electric charge density of the vacuum is zero. In quantum field theory
, a Bogoliubov transformation
on the creation and annihilation operators (turning an occupied negative-energy electron state into an unoccupied positive energy positron state and an unoccupied negative-energy electron state into an occupied positive energy positron state) allows us to bypass the Dirac sea formalism even though, formally, it is equivalent to it.
In certain applications of condensed matter physics
, however, the underlying concepts of "hole theory" are valid. The sea of conduction electrons in an electrical conductor
, called a Fermi sea, contains electrons with energies up to the chemical potential
of the system. An unfilled state in the Fermi sea behaves like a positively-charged electron, though it is referred to as a "hole" rather than a "positron". The negative charge of the Fermi sea is balanced by the positively-charged ionic lattice of the material.
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
formulated by British physicist Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
in 1928. It provided a description of elementary
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
spin-½
Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles...
particles, such as electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s, consistent with both the principles of quantum mechanics and the theory of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, and was the first theory fully to account for relativity in the context of quantum mechanics. It accounted for the fine details of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, antimatter
Antimatter
In particle physics, antimatter is the extension of the concept of the antiparticle to matter, where antimatter is composed of antiparticles in the same way that normal matter is composed of particles...
, hitherto unsuspected and unobserved, and actually predated its experimental discovery. It also provided a theoretical justification for the introduction of several-component wave functions in Pauli's phenomenological theory of spin. Although Dirac did not at first fully appreciate what his own equation was telling him, his resolute faith in the logic of mathematics as a means to physical reasoning, his explanation of spin as a consequence of the union of quantum mechanics and relativity, and the eventual discovery of the positron, represents one of the great triumphs of theoretical physics, fully on a par with the work of Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
, Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, and Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
before him.
Mathematical formulation
The Dirac equation in the form originally proposed by Dirac is :-
- where
- m is the rest massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the electron, - c is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, - p is the momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, understood to be an operator in the sense of the Schrödinger theory, - r and t are the spaceSpaceSpace is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and timeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
coordinates, - ħ is the reduced Planck constantPlanck constantThe Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, h divided by 2π.
- m is the rest mass
Dirac's purpose in casting this equation was to explain the behavior of the relativistically moving electron, and so to allow the atom to be treated in a manner consistent with relativity. His rather modest hope was that the corrections introduced this way might have bearing on the problem of atomic spectra. Up until that time, attempts to make the old quantum theory of the atom compatible with the theory of relativity, attempts based on discretizing the angular momentum stored in the electron's possibly non-circular orbit of the atomic nucleus, had failed - and the new quantum mechanics of Heisenberg, Pauli, Jordan, Schrödinger, and Dirac himself had not developed sufficiently to treat this problem. Although Dirac's original intentions were satisfied, his equation had far deeper implications for the structure of matter, and introduced new mathematical classes of objects that are now essential elements of fundamental physics.
The new elements in this equation are the 4×4 matrices
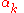and , and the four-component wave functionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
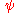. The matrices are all Hermitian and have squares equal to the 4 × 4 identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
:
and they all mutually anticommute:
when i and j are distinct. The single symbolic equation thus unravels into four coupled linear first-order partial differential equations for the four quantities that make up the wave function. These matrices, and the form of the wave function, have a deep mathematical significance. The algebraic structure represented by the Dirac matrices had been created some 50 years earlier by the English mathematician W. K. Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
. In turn, Clifford's ideas had emerged from the mid-19th century work of the German mathematician Hermann Grassmann
Hermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
in his "Lineale Ausdehnungslehre" (Theory of Linear Extensions). The latter had been regarded as well-nigh incomprehensible by most of his contemporaries. The appearance of something so seemingly abstract, at such a late date, and in such a direct physical manner, is one of the most remarkable chapters in the history of physics.
Making the Schrödinger equation relativistic
The Dirac equation is superficially similar to the Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for a free massive particle:
The left side represents the square of the momentum operator divided by twice the mass, which is the non-relativistic kinetic energy. Because relativity treats space and time as a whole, a relativistic generalization of this equation requires that space and time derivatives must enter symmetrically, as they do in the Maxwell equations that govern the behavior of light — the equations must be differentially of the same order in space and time. In relativity, the momentum and the energy are the space and time parts of a space-time vector, the 4-momentum, and they are related by the relativistically invariant relation
which says that the length of this vector is proportional to the rest mass m. Substituting the operator equivalents of the energy and momentum from the Schrödinger theory, we get an equation describing the propagation of waves, constructed from relativistically invariant objects,
with the wave function
being a relativistic scalar: a complex number which has the same numerical value in all frames of reference. The space and time derivatives both enter to second order. This has a telling consequence for the interpretation of the equation. Because the equation is second order in the time derivative, then by the nature of solving differential equations, one must specify both the initial values of the wave function itself and of its first time derivative, in order to solve definite problems. Because both may be specified more or less arbitrarily, the wave function cannot maintain its former role of determining the probability density of finding the electron in a given state of motion. In the Schrödinger theory, the probability density is given by the positive definite expression
and this density is convected according to the probability current vector
with the conservation of probability current and density following from the Schrödinger equation:
The fact that the density is positive definite and convected according to this continuity equation, implies that we may integrate the density over a certain domain and set the total to 1, and this condition will be maintained by the conservation law. A proper relativistic theory with a probability density current must also share this feature. Now, if we wish to maintain the notion of a convected density, then we must generalize the Schrödinger expression of the density and current so that the space and time derivatives again enter symmetrically in relation to the scalar wave function. We are allowed to keep the Schrödinger expression for the current, but must replace by probability density by the symmetrically formed expression
which now becomes the 4th component of a space-time vector, and the entire 4-current density has the relativistically covariant expression
The continuity equation is as before. Everything is compatible with relativity now, but we see immediately that the expression for the density is no longer positive definite - the initial values of both
and may be freely chosen, and the density may thus become negative, something that is impossible for a legitimate probability density. Thus we cannot get a simple generalization of the Schrödinger equation under the naive assumption that the wave function is a relativistic scalar, and the equation it satisfies, second order in time.Although it is not a successful relativistic generalization of the Schrödinger equation, this equation is resurrected in the context of quantum field theory, where it is known as the Klein–Gordon equation, and describes a spinless particle field (e.g. pi meson). Historically, Schrödinger himself arrived at this equation before the one that bears his name, but soon discarded it. In the context of quantum field theory, the indefinite density is understood to correspond to the charge density, which can be positive or negative, and not the probability density.
Dirac's coup
Dirac thus thought to try an equation that was first order in both space and time. One could, for example, formally take the relativistic expression for the energy, replace p by its operator equivalent, expand the square root in an infinite series of derivative operators, set up an eigenvalue problem, then solve the equation formally by iterations. Most physicists had little faith in such a process, even if it were technically possible.As the story goes, Dirac was staring into the fireplace at Cambridge, pondering this problem, when he hit upon the idea of taking the square root of the wave operator thus:
On multiplying out the right side we see that, in order to get all the cross-terms such as
to vanish, we must assume
with
Dirac, who had just then been intensely involved with working out the foundations of Heisenberg's matrix mechanics
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
, immediately understood that these conditions could be met if A, B, C and D are matrices, with the implication that the wave function has multiple components. This immediately explained the appearance of two-component wave functions in Pauli's phenomenological theory of spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, something that up until then had been regarded as mysterious, even to Pauli himself. However, one needs at least 4×4 matrices to set up a system with the properties required — so the wave function had four components, not two, as in the Pauli theory, or one, as in the bare Schrödinger theory. The four-component wave function represents a new class of mathematical object in physical theories, spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s, that makes its first appearance here.
Given the factorization in terms of these matrices, one can now write down immediately an equation
with
to be determined. Applying again the matrix operator on both side yields
On taking
we find that all the components of the wave function individually satisfy the relativistic energy–momentum relation. Thus the sought-for equation that is first-order in both space and time is
Setting
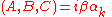and 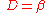, we get the Dirac equation as written above.Covariant form and relativistic invariance
To demonstrate the relativistic invariance of the equation, it is advantageous to cast it into a form in which the space and time derivatives appear on an equal footing. New matrices are introduced as follows:
and the equation takes the form
In practice one often writes the gamma matrices in terms of 2x2 sub-matrices taken from the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
and the 2x2 identity matrix. Explicitly the standard representation is
The complete system is summarized using the Minkowski metric on spacetime in the form
where the bracket expression
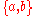means , the anticommutator. These are the defining relations of a Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
over a pseudo-orthogonal 4-d space with metric signature
. The specific Clifford algebra employed in the Dirac equation is known today as the Dirac algebraDirac algebra
In mathematical physics, the Dirac algebra is the Clifford algebra Cℓ1,3 which is generated by matrix multiplication and real and complex linear combination over the Dirac gamma matrices, introduced by the mathematical physicist P. A. M...
. Although not recognized as such by Dirac at the time the equation was formulated, in hindsight the introduction of this geometric algebra represents an enormous stride forward in the development of quantum theory.
The Dirac equation may now be interpreted as an eigenvalue equation, where the rest mass is proportional to an eigenvalue of the 4-momentum operator, the proportion being the speed of light:
In practice, physicists often use units of measure such that
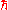and c are equal to 1, known as "natural unitsNatural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
". The equation then takes the simple form
A fundamental theorem states that if two distinct sets of matrices are given that both satisfy the Clifford relations, then they are connected to each other by a similarity transformation:
If in addition the matrices are all unitary
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
, as are the Dirac set, then S itself is unitary;
The transformation U is unique up to a multiplicative factor of absolute value 1. Let us now imagine a Lorentz transformation to have been performed on the space and time coordinates, and on the derivative operators, which form a covariant vector. For the operator
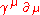to remain invariant, the gammas must transform among themselves as a contravariant vector with respect to their spacetime index. These new gammas will themselves satisfy the Clifford relations, because of the orthogonality of the Lorentz transformation. By the fundamental theorem, we may replace the new set by the old set subject to a unitary transformation. In the new frame, remembering that the rest mass is a relativistic scalar, the Dirac equation will then take the form
If we now define the transformed spinor
then we have the transformed Dirac equation in a way that demonstrates manifest relativistic invariance:
Thus, once we settle on any unitary representation of the gammas, it is final provided we transform the spinor according the unitary transformation that corresponds to the given Lorentz transformation. The various representations of the Dirac matrices employed will bring into focus particular aspects of the physical content in the Dirac wave function (see below). The representation shown here is known as the standard representation - in it, the wave function's upper two components go over into Pauli's 2-spinor wave function in the limit of low energies and small velocities in comparison to light.
The considerations above reveal the origin of the gammas in geometry, hearkening back to Grassmann's original motivation - they represent a fixed basis of unit vectors in spacetime. Similarly, products of the gammas such as
represent oriented surface elements, and so on. With this in mind, we can find the form the unit volume element on spacetime in terms of the gammas as follows. By definition, it is
For this to be an invariant, the epsilon symbol must be a tensor, and so must contain a factor of
, where g is the determinant of the metric tensor. Since this is negative, that factor is imaginary. Thus
This matrix is given the special symbol
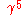, owing to its importance when one is considering improper transformations of spacetime, that is, those that change the orientation of the basis vectors. In the standard representation it is
This matrix will also be found to anticommute with the other four Dirac matrices. It takes a leading role when questions of parity arise, because the volume element as a directed magnitude changes sign under a space-time reflection. Taking the positive square root above thus amounts to choosing a handedness convention on space-time.
Adjoint equation and conservation of probability current
By defining the adjoint spinor
where
is the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of
, and noticing that
-
,
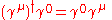we obtain, by taking the Hermitian conjugate of the Dirac equation and multiplying from the right by
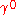, the adjoint equation:
where
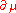is understood to act to the left. Multiplying the Dirac equation by 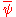from the left, and the adjoint equation by 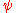from the right, and subtracting, produces the law of conservation of the Dirac current:
Now we see the great advantage of the first-order equation over the one Schrödinger had tried - this is the conserved current density required by relativistic invariance, only now its 4th component is positive definite and thus suitable for the role of a probability density:
Because the probability density now appears as the fourth component of a relativistic vector, and not a simple scalar as in the Schrödinger equation, it will be subject to the usual effects of the Lorentz transformations such as time dilation. Thus for example atomic processes that are observed as rates, will necessarily be adjusted in a way consistent with relativity, while those involving the measurement of energy and momentum, which themselves form a relativistic vector, will undergo parallel adjustment which preserves the relativistic covariance of the observed values.
Comparison with the Pauli theory
The necessity of introducing half-integral spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
goes back experimentally to the results of the Stern–Gerlach experiment
Stern–Gerlach experiment
Important in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
. A beam of atoms is run through a strong inhomogeneous magnetic field, which then splits into N parts depending on the intrinsic angular momentum of the atoms. It was found that for silver atoms, the beam was split in two—the ground state therefore could not be integral, because even if the intrinsic angular momentum of the atoms were as small as possible, 1, the beam would be split into 3 parts, corresponding to atoms with Lz = −1, 0, and +1. The conclusion is that silver atoms have net intrinsic angular momentum of . Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
set up a theory which explained this splitting by introducing a two-component wave function and a corresponding correction term in the Hamiltonian
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
, representing a semi-classical coupling of this wave function to an applied magnetic field, as so:
Here
and represent the electromagnetic field, and the three sigmas are the Pauli matrices. On squaring out the first term, a residual interaction with the magnetic field is found, along with the usual classical Hamiltonian of a charged particle interacting with an applied field:
This Hamiltonian is now a 2 × 2 matrix, so the Schrödinger equation based on it must use a two-component wave function. Pauli had introduced the 2x2 sigma matrices as pure phenomenology— Dirac now had a theoretical argument that implied that spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
was somehow the consequence of the marriage of quantum mechanics to relativity. On introducing the external electromagnetic 4-vector potential into the Dirac equation in a similar way, known as minimal coupling
Minimal coupling
In physics, minimal coupling refers to a coupling between fields which involves only the charge distribution and not higher multipole moments of the charge distribution...
, it takes the form (in natural units)
A second application of the Dirac operator will now reproduce the Pauli term exactly as before, because the spatial Dirac matrices multiplied by i, have the same squaring and commutation properties as the Pauli matrices. What is more, the value of the gyromagnetic ratio of the electron, standing in front of Pauli's new term, is explained from first principles. This was a major achievement of the Dirac equation and gave physicists great faith in its overall correctness. There is more however. The Pauli theory may be seen as the low energy limit of the Dirac theory in the following manner. First the equation is written in the form of coupled equations for 2-spinors with the units restored:
so
Assuming the field is weak and the motion of the electron non-relativistic, we have the total energy of the electron approximately equal to its rest energy, and the momentum going over to the classical value,
and so the second equation may be written
which is of order v/c - thus at typical energies and velocities, the bottom components of the Dirac spinor in the standard representation are much suppressed in comparison to the top components. Substituting this expression into the first equation gives after some rearrangement
The operator on the left represents the particle energy reduced by its rest energy, which is just the classical energy, so we recover Pauli's theory if we identify his 2-spinor with the top components of the Dirac spinor in the non-relativistic approximation. A further approximation gives the Schrödinger equation as the limit of the Pauli theory. Thus the Schrödinger equation may be seen as the far non-relativistic approximation of the Dirac equation when one may neglect spin and work only at low energies and velocities. This also was a great triumph for the new equation, as it traced the mysterious i that appears in it, and the necessity of a complex wave function, back to the geometry of space-time through the Dirac algebra. It also highlights why the Schrödinger equation, although superficially in the form of a diffusion equation, actually represents the propagation of waves.
It should be strongly emphasized that this separation of the Dirac spinor into large and small components depends explicitly on a low-energy approximation. The entire Dirac spinor represents an irreducible whole, and the components we have just neglected to arrive at the Pauli theory will bring in new phenomena in the relativistic regime - antimatter
Antimatter
In particle physics, antimatter is the extension of the concept of the antiparticle to matter, where antimatter is composed of antiparticles in the same way that normal matter is composed of particles...
and the idea of creation and annihilation of particles.
In a general case (if a certain linear function of electromagnetic field does not vanish identically), three out of four components of the spinor function in the Dirac equation can be algebraically eliminated, yielding an equivalent fourth-order partial differential equation for just one component. Furthermore, this remaining component can be made real by a gauge transform.
Dirac equation in curved spacetime
The Dirac equation can be written in curved spacetime using vierbein fields. Vierbeins describe a local frameFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
that enables to define Dirac matrices at every point. Contracting
Tensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
these matrices with vierbeins give the right transformation properties. This way Dirac's equation takes the following form in curved spacetime:
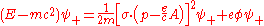
Here
is the vierbein and is the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
for fermion fields, defined as follows
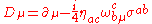
where
is the Lorentzian metric, is the commutator of Dirac matrices:and
is the spin connectionSpin connection
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the Levi-Civita connection...
:
where
is the Christoffel symbol. Note that here, Latin letters denote the "Lorentzian" indices and Greek ones denote "Riemannian" indices.Physical interpretation
The Dirac theory, while providing a wealth of information that is accurately confirmed by experiments, nevertheless introduces a new physical paradigm that appears at first difficult to interpret and even paradoxical. Some of these issues of interpretation must be regarded as open questions. Here we will see how the Dirac theory brilliantly answered some of the outstanding issues in physics at the time it was put forward, while posing others that are still the subject of debate.Identification of observables
The critical physical question in a quantum theory is - what are the physically observable quantities defined by the theory? According to general principles, such quantities are defined by Hermitian operators that act on the Hilbert space of possible states of a system. The eigenvalues of these operators are then the possible results of measuring the corresponding physical quantity. In the Schrödinger theory, the simplest such object is the overall Hamiltonian, which represents the total energy of the system. If we wish to maintain this interpretation on passing to the Dirac theory, we must take the Hamiltonian to be
This looks promising, because we see by inspection the rest energy of the particle and, in case
, the energy of a charge placed in an electric potential 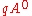. What about the term involving the vector potential? In classical electrodynamics, the energy of a charge moving in an applied potential is
Thus the Dirac Hamiltonian is fundamentally distinguished from its classical counterpart, and we must take great care to correctly identify what is an observable in this theory. Much of the apparent paradoxical behavior implied by the Dirac equation amounts to a misidentification of these observables. Let us now describe one such effect. (cont'd)
Paradoxical behavior
The following problems arise with the Dirac equation, which are not immediately easy to interpret.Klein paradox
Klein paradox
In 1929, physicist Oskar Klein obtained a surprising result by applying the Dirac equation to the familiar problem of electron scattering from a potential barrier. In nonrelativistic quantum mechanics, electron tunneling into a barrier is observed, with exponential damping...
: when a Dirac electron interacts with an electric potential, the total probability is not conserved.
Also, the electron can tunnel into high potential barriers, unlike the case in classical quantum mechanics described by the Schrödinger equation.
Zitterbewegung
Zitterbewegung
Zitterbewegung is a theoretical rapid motion of elementary particles, in particular electrons, that obey the Dirac equation...
: apparent fluctuation (at the speed of light) of the position of an electron around the median.
Hole theory
The negative E solutions found in the preceding section are problematic, for it was assumed that the particle has a positive energy. Mathematically speaking, however, there seems to be no reason for us to reject the negative-energy solutions. Since they exist, we cannot simply ignore them, for once we include the interaction between the electron and the electromagnetic field, any electron placed in a positive-energy eigenstate would decay into negative-energy eigenstates of successively lower energy by emitting excess energy in the form of photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s. Real electrons obviously do not behave in this way.
To cope with this problem, Dirac introduced the hypothesis, known as hole theory, that the vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
is the many-body quantum state in which all the negative-energy electron eigenstates are occupied. This description of the vacuum as a "sea" of electrons is called the Dirac sea
Dirac sea
The Dirac sea is a theoretical model of the vacuum as an infinite sea of particles with negative energy. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons...
. Since the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
forbids electrons from occupying the same state, any additional electron would be forced to occupy a positive-energy eigenstate, and positive-energy electrons would be forbidden from decaying into negative-energy eigenstates.
Dirac further reasoned that if the negative-energy eigenstates are incompletely filled, each unoccupied eigenstate – called a hole – would behave like a positively charged particle. The hole possesses a positive energy, since energy is required to create a particle–hole pair from the vacuum. As noted above, Dirac initially thought that the hole might be the proton, but Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
pointed out that the hole should behave as if it had the same mass as an electron, whereas the proton is over 1800 times heavier. The hole was eventually identified as the positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
, experimentally discovered by Carl Anderson
Carl David Anderson
Carl David Anderson was an American physicist. He is best known for his discovery of the positron in 1932, an achievement for which he received the 1936 Nobel Prize in Physics, and of the muon in 1936.-Biography:...
in 1932.
It is not entirely satisfactory to describe the "vacuum" using an infinite sea of negative-energy electrons. The infinitely negative contributions from the sea of negative-energy electrons has to be canceled by an infinite positive "bare" energy and the contribution to the charge density and current coming from the sea of negative-energy electrons is exactly canceled by an infinite positive "jellium
Jellium
Jellium, also known as the uniform electron gas or homogeneous electron gas , is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space whence the electron densityis a uniform quantity as well in space...
" background so that the net electric charge density of the vacuum is zero. In quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a Bogoliubov transformation
Bogoliubov transformation
In theoretical physics, the Bogoliubov transformation, named after Nikolay Bogolyubov, is a unitary transformation from a unitary representation of some canonical commutation relation algebra or canonical anticommutation relation algebra into another unitary representation, induced by an...
on the creation and annihilation operators (turning an occupied negative-energy electron state into an unoccupied positive energy positron state and an unoccupied negative-energy electron state into an occupied positive energy positron state) allows us to bypass the Dirac sea formalism even though, formally, it is equivalent to it.
In certain applications of condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, however, the underlying concepts of "hole theory" are valid. The sea of conduction electrons in an electrical conductor
Electrical conductor
In physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...
, called a Fermi sea, contains electrons with energies up to the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
of the system. An unfilled state in the Fermi sea behaves like a positively-charged electron, though it is referred to as a "hole" rather than a "positron". The negative charge of the Fermi sea is balanced by the positively-charged ionic lattice of the material.
See also
- Bohr–Sommerfeld theory
- Breit equationBreit equationThe Breit equation is a relativistic wave equation derived by Gregory Breit in 1929 based on the Dirac equation, which formally describes two or more massive spin-1/2 particles interacting electromagnetically to the first order in perturbation theory. It accounts for magnetic interactions and...
- Dirac field
- Einstein-Maxwell-Dirac equationsEinstein-Maxwell-Dirac equationsEinstein-Maxwell-Dirac equations are related to quantum field theory. The current Big Bang Model is a quantum field theory in a curved spacetime. Unfortunately, no such theory is mathematically well-defined; in spite of this, theoreticians claim to extract information from this hypothetical theory...
- Feynman checkerboardFeynman checkerboardThe Feynman Checkerboard or Relativistic Chessboard model was Richard Feynman’s sum-over-paths formulation of the kernel for a free spin ½ particle moving in one spatial dimension...
- Foldy–Wouthuysen transformation
- Klein–Gordon equation
- Quantum electrodynamicsQuantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
- Rarita–Schwinger equation
- Theoretical and experimental justification for the Schrödinger equationTheoretical and experimental justification for the Schrödinger equationThe theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles...
- The Dirac Equation appears on the floor of Westminster AbbeyWestminster AbbeyThe Collegiate Church of St Peter at Westminster, popularly known as Westminster Abbey, is a large, mainly Gothic church, in the City of Westminster, London, United Kingdom, located just to the west of the Palace of Westminster. It is the traditional place of coronation and burial site for English,...
. It appears on the plaque commemorating Paul Dirac's life which was inaugurated on November 13, 1995.
Selected papers
- P.A.M. Dirac "The Quantum Theory of the Electron", Proc. R. Soc. A (1928) vol. 117, no 778, 610-624
- P.A.M. Dirac "The Quantum Theory of the Electron", Proc. R. Soc. A117) link to the volume of the Proceedings of the Royal Society of London containing the article at page 610
- P.A.M. Dirac "A Theory of Electrons and Protons", Proc. R. Soc. A126) link to the volume of the Proceedings of the Royal Society of London containing the article at page 360
- C.D. Anderson, Phys. Rev. 43, 491 (1933)
- R. Frisch and O. Stern, Z. Phys. 85, 4 (1933)
Textbooks
- Dirac, P.A.M., Principles of Quantum Mechanics, 4th edition (Clarendon, 1982)
- Shankar, R., Principles of Quantum Mechanics, 2nd edition (Plenum, 1994)
- Bjorken, J D & Drell, S, Relativistic Quantum mechanics
- Thaller, B., The Dirac Equation, Texts and Monographs in Physics (Springer, 1992)
- Schiff, L.I., Quantum Mechanics, 3rd edition (McGraw-Hill, 1968)
- Griffiths, D.J., Introduction to Elementary Particles, 2nd edition (Wiley-VCH, 2008) ISBN 978-3-527-40601-2.
External links
- The Dirac Equation at MathPages
- The Nature of the Dirac Equation, its solutions and Spin
- Dirac equation for a spin ½ particle
- Pedagogic Aids to Quantum Field Theory click on Chap. 4 for a step-by-small-step introduction to the Dirac equation, spinors, and relativistic spin/helicity operators.