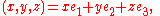Orthonormal basis
Encyclopedia
In mathematics
, particularly linear algebra
, an orthonormal basis for inner product space
V with finite dimension is a basis
for V whose vectors are orthonormal. For example, the standard basis
for a Euclidean space
Rn is an orthonormal basis, where the relevant inner product is the dot product
of vectors. The image
of the standard basis under a rotation
or reflection
(or any orthogonal transformation) is also orthonormal, and every orthonormal basis for Rn arises in this fashion.
For a general inner product space V, an orthonormal basis can be used to define normalized orthogonal coordinates
on V. Under these coordinates, the inner product becomes dot product of vectors. Thus the presence of an orthonormal basis reduces the study of a finite-dimensional
inner product space to the study of Rn under dot product. Every finite-dimensional inner product space has an orthonormal basis, which may be obtained from an arbitrary basis using the Gram–Schmidt process
.
In functional analysis
, the concept of an orthonormal basis can be generalized to arbitrary (infinite-dimensional) inner product spaces (or pre-Hilbert spaces). Given a pre-Hilbert space H, an orthonormal basis for H is an orthonormal set of vectors with the property that every vector in H can be written as an infinite linear combination of the vectors in the basis. In this case, the orthonormal basis is sometimes called a Hilbert basis for H. Note that an orthonormal basis in this sense is not generally a Hamel basis, since infinite linear combinations are required. Specifically, the linear span
of the basis must be dense
in H, but it may not be the entire space.
When B is orthonormal, we have instead
and the norm
of x can be given by
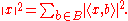
Even if B is uncountable
, only countably many terms in this sum will be non-zero, and the expression is therefore well-defined. This sum is also called the Fourier expansion of x, and the formula is usually known as Parseval's identity
. See also Generalized Fourier series
.
If B is an orthonormal basis of H, then H is isomorphic to ℓ 2(B) in the following sense: there exists a bijective linear map Φ : H -> ℓ 2(B) such that
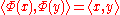
for all x and y in H.
(or more simply well-ordering and transfinite recursion), one can show that every Hilbert space admits a basis and thus an orthonormal basis; furthermore, any two orthonormal bases of the same space have the same cardinality
(this can be proven in a manner akin to that of the proof of the usual dimension theorem for vector spaces
, with separate cases depending on whether the larger basis candidate is countable or not). A Hilbert space is separable if and only if it admits a countable orthonormal basis.
for the orthogonal group
O(n), and is called the Stiefel manifold
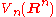of orthonormal n-frames
.
In other words, the space of orthonormal bases is like the orthogonal group, but without a choice of base point: given an orthogonal space, there is no natural choice of orthonormal basis, but once one is given one, there is a one-to-one correspondence between bases and the orthogonal group.
Concretely, a linear map is determined by where it sends a given basis: just as an invertible map can take any basis to any other basis, an orthogonal map can take any orthogonal basis to any other orthogonal basis.
The other Stiefel manifolds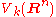
for 
of incomplete orthonormal bases (orthonormal k-frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k-frame can be taken to any other k-frame by an orthogonal map, but this map is not uniquely determined.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, an orthonormal basis for inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
V with finite dimension is a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for V whose vectors are orthonormal. For example, the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
for a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is an orthonormal basis, where the relevant inner product is the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of vectors. The image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the standard basis under a rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
or reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
(or any orthogonal transformation) is also orthonormal, and every orthonormal basis for Rn arises in this fashion.
For a general inner product space V, an orthonormal basis can be used to define normalized orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
on V. Under these coordinates, the inner product becomes dot product of vectors. Thus the presence of an orthonormal basis reduces the study of a finite-dimensional
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
inner product space to the study of Rn under dot product. Every finite-dimensional inner product space has an orthonormal basis, which may be obtained from an arbitrary basis using the Gram–Schmidt process
Gram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
.
In functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the concept of an orthonormal basis can be generalized to arbitrary (infinite-dimensional) inner product spaces (or pre-Hilbert spaces). Given a pre-Hilbert space H, an orthonormal basis for H is an orthonormal set of vectors with the property that every vector in H can be written as an infinite linear combination of the vectors in the basis. In this case, the orthonormal basis is sometimes called a Hilbert basis for H. Note that an orthonormal basis in this sense is not generally a Hamel basis, since infinite linear combinations are required. Specifically, the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the basis must be dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in H, but it may not be the entire space.
Examples
- The set of vectors {e1 = (1, 0, 0), e2 = (0, 1, 0), e3 = (0, 0, 1)} (the standard basis) forms an orthonormal basis of R3.
-
- Proof: A straightforward computation shows that the inner products of these vectors equals zero, <e1, e2> = <e1, e3> = <e2, e3> = 0 and that each of their magnitudes equals one, ||e1|| = ||e2|| = ||e3|| = 1. This means {e1, e2, e3} is an orthonormal set. All vectors (x, y, z) in R3 can be expressed as a sum of the basis vectors scaled
- so {e1,e2,e3} spans R3 and hence must be a basis. It may also be shown that the standard basis rotated about an axis through the origin or reflected in a plane through the origin forms an orthonormal basis of R3.
- The set {fn : n ∈ Z} with fn(x) = expExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
(2πinx) forms an orthonormal basis of the complex space L2([0,1]). This is fundamental to the study of Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. - The set {eb : b ∈ B} with eb(c) = 1 if b = c and 0 otherwise forms an orthonormal basis of ℓ 2(B).
- Eigenfunctions of a Sturm–Liouville eigenproblem.
- An orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
is a matrix whose column vectors form an orthonormal set.
- The set {fn : n ∈ Z} with fn(x) = exp
- Proof: A straightforward computation shows that the inner products of these vectors equals zero, <e1, e2> = <e1, e3> = <e2, e3> = 0 and that each of their magnitudes equals one, ||e1|| = ||e2|| = ||e3|| = 1. This means {e1, e2, e3} is an orthonormal set. All vectors (x, y, z) in R3 can be expressed as a sum of the basis vectors scaled
Basic formula
If B is an orthogonal basis of H, then every element x of H may be written asWhen B is orthonormal, we have instead
and the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of x can be given by
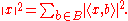
Even if B is uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
, only countably many terms in this sum will be non-zero, and the expression is therefore well-defined. This sum is also called the Fourier expansion of x, and the formula is usually known as Parseval's identity
Parseval's identity
In mathematical analysis, Parseval's identity is a fundamental result on the summability of the Fourier series of a function. Geometrically, it is thePythagorean theorem for inner-product spaces....
. See also Generalized Fourier series
Generalized Fourier series
In mathematical analysis, many generalizations of Fourier series have proved to be useful.They are all special cases of decompositions over an orthonormal basis of an inner product space....
.
If B is an orthonormal basis of H, then H is isomorphic to ℓ 2(B) in the following sense: there exists a bijective linear map Φ : H -> ℓ 2(B) such that
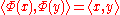
for all x and y in H.
Incomplete orthogonal sets
Given a Hilbert space H and a set S of mutually orthogonal vectors in H, we can take the smallest closed linear subspace V of H containing S. Then S will be an orthogonal basis of V; which may of course be smaller than H itself, being an incomplete orthogonal set, or be H, when it is a complete orthogonal set.Existence
Using Zorn's lemma and the Gram–Schmidt processGram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
(or more simply well-ordering and transfinite recursion), one can show that every Hilbert space admits a basis and thus an orthonormal basis; furthermore, any two orthonormal bases of the same space have the same cardinality
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
(this can be proven in a manner akin to that of the proof of the usual dimension theorem for vector spaces
Dimension theorem for vector spaces
In mathematics, the dimension theorem for vector spaces states that all bases of a vector space have equally many elements. This number of elements may be finite, or given by an infinite cardinal number, and defines the dimension of the space....
, with separate cases depending on whether the larger basis candidate is countable or not). A Hilbert space is separable if and only if it admits a countable orthonormal basis.
As a homogeneous space
The set of orthonormal bases for a space is a principal homogeneous spacePrincipal homogeneous space
In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
for the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n), and is called the Stiefel manifold
Stiefel manifold
In mathematics, the Stiefel manifold Vk is the set of all orthonormal k-frames in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel...
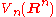of orthonormal n-framesK-frame
In linear algebra, a branch of mathematics, a k-frame is an ordered set of k linearly independent vectors in a space; thus k ≤ n, where n is the dimension of the vector space, and if k = n an n-frame is precisely an ordered basis.If the vectors are orthogonal, or orthonormal,...
.
In other words, the space of orthonormal bases is like the orthogonal group, but without a choice of base point: given an orthogonal space, there is no natural choice of orthonormal basis, but once one is given one, there is a one-to-one correspondence between bases and the orthogonal group.
Concretely, a linear map is determined by where it sends a given basis: just as an invertible map can take any basis to any other basis, an orthogonal map can take any orthogonal basis to any other orthogonal basis.
The other Stiefel manifolds
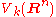for of incomplete orthonormal bases (orthonormal k-frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k-frame can be taken to any other k-frame by an orthogonal map, but this map is not uniquely determined.