
Interpretation of quantum mechanics
Encyclopedia
An interpretation of quantum mechanics is a set of statements which attempt to explain how quantum mechanics
informs our understanding
of nature
. Although quantum mechanics has held up to rigorous and thorough experimental testing, many of these experiments are open to different interpretations. There exist a number of contending schools of thought, differing over whether quantum mechanics can be understood to be deterministic
, which elements of quantum mechanics can be considered "real", and other matters.
This question is of special interest to philosophers of physics
, as physicists continue to show a strong interest in the subject. They usually consider an interpretation of quantum mechanics as an interpretation of the mathematical formalism
of quantum mechanics, specifying the physical meaning of the mathematical entities of the theory.
s and matrix mechanics
) progressed through many stages. For instance, Schrödinger
originally viewed the wavefunction associated with the electron
as corresponding to the charge density of an object smeared out over an extended, possibly infinite, volume of space.
Max Born
interpreted it as simply corresponding to a probability distribution
. These are two different interpretations of the wavefunction. In one it corresponds to a material field; in the other it corresponds to a probability distribution — specifically, the probability that the quantum of charge is located at any particular point within spatial dimensions.
The Copenhagen interpretation
was traditionally the most popular among physicists, next to a purely instrumentalist
position that denies any need for explanation (a view expressed in David Mermin
's famous quote "shut up and calculate", often misattributed to Richard Feynman
.) However, the many-worlds interpretation
has been gaining acceptance; a poll mentioned in "The Physics of Immortality" (published in 1994), of 72 "leading cosmologists and other quantum field theorists" found that 58% supported the many-worlds interpretation, including Stephen Hawking
and Nobel laureates Murray Gell-Mann
and Richard Feynman. Moreover, the instrumentalist position has been challenged by proposals for falsifiable experiments that might one day distinguish interpretations, e.g. by measuring an AI consciousness or via quantum computing
.
— a set of equations and formulae for generating results and predictions — and a phenomenology
, a set of observations, including both those obtained by empirical research, and more informal subjective ones (the fact that humans invariably observe an unequivocal world is important in the interpretation of quantum mechanics) . These are the more-or-less fixed ingredients of an interpretation. The ingredients that vary between interpretations are the ontology
and the epistemology, which are concerned with what, if anything, the interpreted theory is "really about". The same phenomenon may be given an ontological reading under one interpretation, and an epistemological one under another. For instance, indeterminism
may be attributed to the real existence of a "maybe" in the universe (ontology) or to limitations of an observer's information and predictive abilities (epistemology). Interpretations may be broadly classed as leaning more towards ontology, i.e. realism
, or towards anti-realism.
Some approaches tend to avoid giving any interpretation of phenomena or formalism. These can be described as instrumentalist. Other approaches suggest modifications to the formalism, and are therefore, strictly speaking, alternative theories rather than interpretations. In some cases, for instance Bohmian mechanics, it is open to debate as to whether an approach is equivalent to the standard formalism.
Firstly, the accepted mathematical structure
of quantum mechanics is based on fairly abstract mathematics, such as Hilbert space
s and operators
on those spaces. In classical mechanics
and electromagnetism
, on the other hand, properties of a point mass or properties of a field are described by real number
s or function
s defined on two or three dimensional sets. These have direct, spatial meaning, and in these theories there seems to be less need to provide special interpretation for those numbers or functions.
Furthermore, the process of measurement
may play an essential role in quantum theory - a hotly contested point. The world around us seems to be in a specific state, but quantum mechanics describes it by wave functions that govern the probability of all values. In general, the wave-function assigns non-zero probabilities to all possible values of any given physical quantity, such as position. How, then, do we see a particle in a specific position when its wave function is spread across all space? In order to describe how specific outcomes arise from the probabilities, the direct interpretation introduced the concept of measurement. According to the theory, wave functions interact with each other and evolve in time in accordance with the laws of quantum mechanics until a measurement is performed, at which point the system takes on one of its possible values, with a probability that's governed by the wave-function. Measurement can interact with the system state in somewhat peculiar ways, as is illustrated by the double-slit experiment
.
Thus the mathematical formalism used to describe the time evolution
of a non-relativistic system proposes two opposed kinds of transformation:
A solution to the problem of interpretation consists in providing some form of plausible picture, by resolving the second kind of transformation. This can be achieved by purely mathematical solutions, as offered by the many-worlds
or the consistent histories
interpretations.
In addition to the unpredictable and irreversible character of measurement processes, there are other elements of quantum physics that distinguish it sharply from classical physics and which are not present in any classical theory. One of these is the phenomenon of entanglement
, as illustrated in the EPR paradox
, which seemingly violates
principles of local causality
.
Another obstruction to interpretation is the phenomenon of complementarity
, which seems to violate basic principles of propositional logic
. Complementarity says there is no logical picture (one obeying classical propositional logic) that can simultaneously describe and be used to reason about all properties of a quantum system S. This is often phrased by saying that there are "complementary" propositions A and B that can each describe S, but not at the same time. Examples of A and B are propositions using a wave description of S and a corpuscular description of S. The latter statement is one part of Niels Bohr
's original formulation, which is often equated to the principle of complementarity itself.
Complementarity does not usually imply that it is classical logic which is at fault (although Hilary Putnam
did take that view in his paper "Is logic empirical?
"). Rather, complementarity means that the composition of physical properties for S (such as position and momentum both having values within certain ranges), using propositional connectives, does not obey the rules of classical propositional logic (see also Quantum logic
). As is now well-known (Omnès, 1999) the "origin of complementarity lies in the non-commutativity of [the] operators" that describe observables (i.e., particles) in quantum mechanics.
Because the complexity of a quantum system is exponential in its number of degrees of freedom, it is difficult to overlap the quantum and classical descriptions to see how the classical approximations are being made.
cannot match the precision of quantum mechanics mathematics, anything said outside the mathematical formulation is necessarily limited in accuracy.
Also, the precise ontological status of each interpretation remains a matter of philosophical argument. In other words, if we interpret the formal structure X of quantum mechanics by means of a structure Y (via a mathematical equivalence of the two structures), what is the status of Y? This is the old question of saving the phenomena
, in a new guise.
Some physicists, for example Asher Peres
and Chris Fuchs, argue that an interpretation is nothing more than a formal equivalence between sets of rules for operating on experimental data, thereby implying that the whole exercise of interpretation is unnecessary.
-value quantity is performed many times, each time starting with the same initial conditions, the outcome is a well-defined probability distribution
agreeing with the real numbers; moreover, quantum mechanics provides a computational instrument to determine statistical properties of this distribution, such as its expectation value
.
Calculations for measurements performed on a system S postulate a Hilbert space
H over the complex numbers. When the system S is prepared in a pure state, it is associated with a vector in H. Measurable quantities are associated with Hermitian operators acting on H: these are referred to as observable
s.
Repeated measurement of an observable A where S is prepared in state ψ yields a distribution of values. The expectation value of this distribution is given by the expression
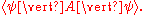
This mathematical machinery gives a simple, direct way to compute a statistical property of the outcome of an experiment, once it is understood how to associate the initial state with a Hilbert space vector, and the measured quantity with an observable (that is, a specific Hermitian operator).
As an example of such a computation, the probability of finding the system in a given state is given by computing the expectation value of a (rank-1) projection operator
is given by computing the expectation value of a (rank-1) projection operator

The probability is then the non-negative real number given by
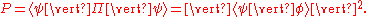
By abuse of language, a bare instrumentalist description could be referred to as an interpretation, although this usage is somewhat misleading since instrumentalism explicitly avoids any explanatory role; that is, it does not attempt to answer the question why.
of the formal mathematics of quantum mechanics) can be characterized by its treatment of certain matters addressed by Einstein, such as:
To explain these properties, we need to be more explicit about the kind of picture an interpretation provides. To that end we will regard an interpretation as a correspondence between the elements of the mathematical formalism M and the elements of an interpreting structure I, where:
The crucial aspect of an interpretation is whether the elements of I are regarded as physically real. Hence the bare instrumentalist view of quantum mechanics outlined in the previous section is not an interpretation at all, for it makes no claims about elements of physical reality.
The current usage of realism and completeness originated in the 1935 paper in which Einstein and others proposed the EPR paradox
. In that paper the authors proposed the concepts element of reality and the completeness of a physical theory. They characterised element of reality as a quantity whose value can be predicted with certainty before measuring or otherwise disturbing it, and defined a complete physical theory as one in which every element of physical reality is accounted for by the theory. In a semantic view of interpretation, an interpretation is complete if every element of the interpreting structure is present in the mathematics. Realism is also a property of each of the elements of the maths; an element is real if it corresponds to something in the interpreting structure. For example, in some interpretations of quantum mechanics (such as the many-worlds interpretation) the ket vector associated to the system state is said to correspond to an element of physical reality, while in other interpretations it is not.
Determinism is a property characterizing state changes due to the passage of time, namely that the state at a future instant is a function
of the state in the present (see time evolution
). It may not always be clear whether a particular interpretation is deterministic or not, as there may not be a clear choice of a time parameter. Moreover, a given theory may have two interpretations, one of which is deterministic and the other not.
Local realism has two aspects:
A precise formulation of local realism in terms of a local hidden variable theory
was proposed by John Bell
.
Bell's theorem
, combined with experimental testing, restricts the kinds of properties a quantum theory can have. For instance, Bell's theorem implies that quantum mechanics cannot satisfy local realism.
is the "standard" interpretation of quantum mechanics formulated by Niels Bohr
and Werner Heisenberg
while collaborating in Copenhagen around 1927. Bohr and Heisenberg extended the probabilistic interpretation of the wavefunction proposed originally by Max Born. The Copenhagen interpretation rejects questions like "where was the particle before I measured its position?" as meaningless. The measurement process randomly picks out exactly one of the many possibilities allowed for by the state's wave function in a manner consistent with the well-defined probabilities that are assigned to each possible state. According to the interpretation, the interaction of an observer or apparatus that is external to the quantum system is the cause of wave function collapse, thus according to Heisenberg "reality is in the observations, not in the electron".
is an interpretation of quantum mechanics in which a universal wavefunction
obeys the same deterministic, reversible
laws at all times; in particular there is no (indeterministic and irreversible
) wavefunction collapse
associated with measurement. The phenomena associated with measurement are claimed to be explained by decoherence
, which occurs when states interact with the environment producing entanglement
, repeatedly splitting the universe into mutually unobservable alternate histories—distinct universes within a greater multiverse
.
interpretation generalizes the conventional Copenhagen interpretation and attempts to provide a natural interpretation of quantum cosmology
. The theory is based on a consistency criterion that allows the history of a system to be described so that the probabilities for each history obey the additive rules of classical probability. It is claimed to be consistent with the Schrödinger equation
.
According to this interpretation, the purpose of a quantum-mechanical theory is to predict the relative probabilities of various alternative histories (for example, of a particle).
, also called the statistical interpretation, can be viewed as a minimalist interpretation. That is, it claims to make the fewest assumptions associated with the standard mathematics. It takes the statistical interpretation of Born to the fullest extent. The interpretation states that the wave function does not apply to an individual system for example, a single particle but is an abstract statistical quantity that only applies to an ensemble (a vast multitude) of similarly prepared systems or particles. Probably the most notable supporter of such an interpretation was Einstein:
The most prominent current advocate of the ensemble interpretation is Leslie E. Ballentine, Professor at Simon Fraser University
, author of the graduate level text book Quantum Mechanics, A Modern Development. An experiment illustrating the ensemble interpretation is provided in Akira Tonomura's Video clip 1
. It is evident from this double-slit experiment
with an ensemble of individual electrons that, since the quantum mechanical wave function (absolutely squared) describes the completed interference pattern, it must describe an ensemble.
to include measurements. Particles, which always have positions, are guided by the wavefunction. The wavefunction evolves according to the Schrödinger wave equation, and the wavefunction never collapses. The theory takes place in a single space-time, is non-local
, and is deterministic. The simultaneous determination of a particle's position and velocity is subject to the usual uncertainty principle
constraint. The theory is considered to be a hidden variable theory
, and by embracing non-locality it satisfies Bell's inequality. The measurement problem
is resolved, since the particles have definite positions at all times. Collapse is explained as phenomenological.
, following the precedent of special relativity
, is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" eigenstate, while to another observer at the same time, it may be in a superposition of two or more states. Consequently, if quantum mechanics is to be a complete theory, relational quantum mechanics argues that the notion of "state" describes not the observed system itself, but the relationship, or correlation, between the system and its observer(s). The state vector
of conventional quantum mechanics becomes a description of the correlation of some degrees of freedom in the observer, with respect to the observed system. However, it is held by relational quantum mechanics that this applies to all physical objects, whether or not they are conscious or macroscopic. Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. Thus the physical content of the theory has to do not with objects themselves, but the relations between them.
An independent relational approach to quantum mechanics
was developed in analogy with David Bohm's elucidation of special relativity, in which a detection event is regarded as establishing a relationship between the quantized field and the detector. The inherent ambiguity associated with applying Heisenberg's uncertainty principle is subsequently avoided.
of quantum mechanics (TIQM) by John G. Cramer
is an interpretation of quantum mechanics inspired by the Wheeler–Feynman absorber theory. It describes quantum interactions in terms of a standing wave formed by retarded (forward-in-time) and advanced (backward-in-time) waves. The author argues that it avoids the philosophical problems with the Copenhagen interpretation and the role of the observer, and resolves various quantum paradoxes.
was suggested by Princeton University
professor Edward Nelson
in 1966. Similar considerations had previously been published, for example by R. Fürth (1933), I. Fényes (1952), and Walter Weizel
(1953), and are referenced in Nelson's paper. More recent work on the stochastic interpretation has been done by M. Pavon. An alternative stochastic interpretation was developed by Roumen Tsekov.
in regarding both the wavefunction and the process of collapse as ontologically objective. In objective theories, collapse occurs randomly ("spontaneous localization"), or when some physical threshold is reached, with observers having no special role. Thus, they are realistic, indeterministic, no-hidden-variables theories. The mechanism of collapse is not specified by standard quantum mechanics, which needs to be extended if this approach is correct, meaning that Objective Collapse is more of a theory than an interpretation. Examples include the Ghirardi-Rimini-Weber theory
and the Penrose interpretation
.
deeply analyzed the so-called measurement problem
. He concluded that the entire physical universe could be made subject to the Schrödinger equation (the universal wave function). Since something "outside the calculation" was needed to collapse the wave function, von Neumann concluded that the collapse was caused by the consciousness of the experimenter. This point of view was later more prominently expanded on by Eugene Wigner, but remains a view held by very few physicists.
Variations of the von Neumann interpretation include:
Other physicists have elaborated their own variations of the von Neumann interpretation; including:
extends the many-worlds interpretation
by proposing that the distinction between worlds should be made at the level of the mind of an individual observer.
can be regarded as a kind of propositional logic suitable for understanding the apparent anomalies regarding quantum measurement, most notably those concerning composition of measurement operations of complementary variables. This research area and its name originated in the 1936 paper by Garrett Birkhoff
and John von Neumann
, who attempted to reconcile some of the apparent inconsistencies of classical boolean logic with the facts related to measurement and observation in quantum mechanics.
describes several versions:
: events in the future can affect ones in the past, exactly as events in the past can affect ones in the future. In these theories, a single measurement cannot fully determine the state of a system (making them a type of hidden variables theory), but given two measurements performed at different times, it is possible to calculate the exact state of the system at all intermediate times. The collapse of the wavefunction is therefore not a physical change to the system, just a change in our knowledge of it due to the second measurement. Similarly, they explain entanglement as not being a true physical state but just an illusion created by ignoring retrocausality. The point where two particles appear to "become entangled" is simply a point where each particle is being influenced by events that occur to the other particle in the future.
BST has applications to Bells theorem, quantum computation and quantum gravity. It also has some resemblance to hidden variable theories and the ensemble interpretation.: particles in BST have multiple well defined trajectories at the microscopic level. These can only be treated stochastically at a coarse grained level, in line
with the ensemble interpretation.
ideas of quantum mysticism
.
No experimental evidence exists that distinguishes among these interpretations. To that extent, the physical theory stands, and is consistent with itself and with reality; difficulties arise only when one attempts to "interpret" the theory. Nevertheless, designing experiments which would test the various interpretations is the subject of active research.
Most of these interpretations have variants. For example, it is difficult to get a precise definition of the Copenhagen interpretation as it was developed and argued about by many people.
According to Bohr, the concept of a physical state independent of the conditions of its experimental observation does not have a well-defined meaning. According to Heisenberg the wavefunction represents a probability, but not an objective reality itself in space and time. According to the Copenhagen interpretation, the wavefunction collapses when a measurement is performed. Both particle AND guiding wavefunction are real. Unique particle history, but multiple wave histories. But quantum logic is more limited in applicability than Coherent Histories. Quantum mechanics is regarded as a way of predicting observations, or a theory of measurement. Observers separate the universal wavefunction into orthogonal sets of experiences. If wavefunction is real then this becomes the many-worlds interpretation. If wavefunction less than real, but more than just information, then Zurek calls this the "existential interpretation". In the TI the collapse of the state vector is interpreted as the completion of the transaction between emitter and absorber. Comparing histories between systems in this interpretation has no well-defined meaning. Any physical interaction is treated as a collapse event relative to the systems involved, not just macroscopic or conscious observers. The state of the system is observer-dependent, i.e., the state is specific to the reference frame of the observer. Caused by the fact that Popper holds both CFD and locality to be true, it is under dispute whether Popper's interpretation can really be considered an interpretation of Quantum Mechanics (which is what Popper claimed) or whether it must be considered a modification of Quantum Mechanics (which is what many Physicists claim), and, in case of the latter, if this modification has been empirically refuted or not. Popper exchanged many long letters with Einstein, Bell etc. about the issue.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
informs our understanding
Understanding
Understanding is a psychological process related to an abstract or physical object, such as a person, situation, or message whereby one is able to think about it and use concepts to deal adequately with that object....
of nature
Nature
Nature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
. Although quantum mechanics has held up to rigorous and thorough experimental testing, many of these experiments are open to different interpretations. There exist a number of contending schools of thought, differing over whether quantum mechanics can be understood to be deterministic
Determinism
Determinism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
, which elements of quantum mechanics can be considered "real", and other matters.
This question is of special interest to philosophers of physics
Philosophy of physics
In philosophy, the philosophy of physics studies the fundamental philosophical questions underlying modern physics, the study of matter and energy and how they interact. The philosophy of physics begins by reflecting on the basic metaphysical and epistemological questions posed by physics:...
, as physicists continue to show a strong interest in the subject. They usually consider an interpretation of quantum mechanics as an interpretation of the mathematical formalism
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
of quantum mechanics, specifying the physical meaning of the mathematical entities of the theory.
Historical background
The definition of terms used by researchers in quantum theory (such as wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
s and matrix mechanics
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
) progressed through many stages. For instance, Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
originally viewed the wavefunction associated with the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
as corresponding to the charge density of an object smeared out over an extended, possibly infinite, volume of space.
Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
interpreted it as simply corresponding to a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. These are two different interpretations of the wavefunction. In one it corresponds to a material field; in the other it corresponds to a probability distribution — specifically, the probability that the quantum of charge is located at any particular point within spatial dimensions.
The Copenhagen interpretation
Copenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
was traditionally the most popular among physicists, next to a purely instrumentalist
Instrumentalism
In the philosophy of science, instrumentalism is the view that a scientific theory is a useful instrument in understanding the world. A concept or theory should be evaluated by how effectively it explains and predicts phenomena, as opposed to how accurately it describes objective...
position that denies any need for explanation (a view expressed in David Mermin
David Mermin
Nathaniel David Mermin is a solid-state physicist at Cornell University best known for the eponymous Mermin-Wagner theorem and his application of the term "Boojum" to superfluidity, and for the quote "Shut up and calculate!"Together with Neil W...
's famous quote "shut up and calculate", often misattributed to Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
.) However, the many-worlds interpretation
Many-worlds interpretation
The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...
has been gaining acceptance; a poll mentioned in "The Physics of Immortality" (published in 1994), of 72 "leading cosmologists and other quantum field theorists" found that 58% supported the many-worlds interpretation, including Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
and Nobel laureates Murray Gell-Mann
Murray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
and Richard Feynman. Moreover, the instrumentalist position has been challenged by proposals for falsifiable experiments that might one day distinguish interpretations, e.g. by measuring an AI consciousness or via quantum computing
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
.
The nature of interpretation
What interpretations are interpretations of is a formalismScientific formalism
Scientific formalism is a broad term for a family of approaches to the presentation of science. It is viewed as an important part of the scientific method, especially in the physical sciences.-Levels of formalism:...
— a set of equations and formulae for generating results and predictions — and a phenomenology
Phenomenology (science)
The term phenomenology in science is used to describe a body of knowledge that relates empirical observations of phenomena to each other, in a way that is consistent with fundamental theory, but is not directly derived from theory. For example, we find the following definition in the Concise...
, a set of observations, including both those obtained by empirical research, and more informal subjective ones (the fact that humans invariably observe an unequivocal world is important in the interpretation of quantum mechanics) . These are the more-or-less fixed ingredients of an interpretation. The ingredients that vary between interpretations are the ontology
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
and the epistemology, which are concerned with what, if anything, the interpreted theory is "really about". The same phenomenon may be given an ontological reading under one interpretation, and an epistemological one under another. For instance, indeterminism
Indeterminism
Indeterminism is the concept that events are not caused, or not caused deterministically by prior events. It is the opposite of determinism and related to chance...
may be attributed to the real existence of a "maybe" in the universe (ontology) or to limitations of an observer's information and predictive abilities (epistemology). Interpretations may be broadly classed as leaning more towards ontology, i.e. realism
Realism
Realism, Realist or Realistic are terms that describe any manifestation of philosophical realism, the belief that reality exists independently of observers, whether in philosophy itself or in the applied arts and sciences. In this broad sense it is frequently contrasted with Idealism.Realism in the...
, or towards anti-realism.
Some approaches tend to avoid giving any interpretation of phenomena or formalism. These can be described as instrumentalist. Other approaches suggest modifications to the formalism, and are therefore, strictly speaking, alternative theories rather than interpretations. In some cases, for instance Bohmian mechanics, it is open to debate as to whether an approach is equivalent to the standard formalism.
Problems of Interpretation
The difficulties of interpretation reflect a number of points about the orthodox description of quantum mechanics, including:- The abstract, mathematical nature of that description.
- The existence of what appear to be non-deterministicQuantum indeterminacyQuantum indeterminacy is the apparent necessary incompleteness in the description of a physical system, that has become one of the characteristics of the standard description of quantum physics...
and irreversible processes. - The phenomenon of entanglementQuantum entanglementQuantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
, and in particular the correlations between remote events that are not expected in classical theory. - The complementarity of the proffered descriptions of reality.
- The role played by observers and the process of measurementMeasurement in quantum mechanicsThe framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
. - The rapid rate at which quantum descriptions become more complicated as the size of a system increases.
Firstly, the accepted mathematical structure
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
of quantum mechanics is based on fairly abstract mathematics, such as Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s and operators
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
on those spaces. In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, on the other hand, properties of a point mass or properties of a field are described by real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s defined on two or three dimensional sets. These have direct, spatial meaning, and in these theories there seems to be less need to provide special interpretation for those numbers or functions.
Furthermore, the process of measurement
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
may play an essential role in quantum theory - a hotly contested point. The world around us seems to be in a specific state, but quantum mechanics describes it by wave functions that govern the probability of all values. In general, the wave-function assigns non-zero probabilities to all possible values of any given physical quantity, such as position. How, then, do we see a particle in a specific position when its wave function is spread across all space? In order to describe how specific outcomes arise from the probabilities, the direct interpretation introduced the concept of measurement. According to the theory, wave functions interact with each other and evolve in time in accordance with the laws of quantum mechanics until a measurement is performed, at which point the system takes on one of its possible values, with a probability that's governed by the wave-function. Measurement can interact with the system state in somewhat peculiar ways, as is illustrated by the double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
.
Thus the mathematical formalism used to describe the time evolution
Time evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...
of a non-relativistic system proposes two opposed kinds of transformation:
- Reversible transformations described by unitary operatorUnitary operatorIn functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s on the state space. These transformations are determined by solutions to the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
.
- Non-reversible and unpredictable transformations described by mathematically more complicated transformations (see quantum operationQuantum operationIn quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
s). Examples include the transformations undergone by a system as a result of measurement.
A solution to the problem of interpretation consists in providing some form of plausible picture, by resolving the second kind of transformation. This can be achieved by purely mathematical solutions, as offered by the many-worlds
Many-worlds interpretation
The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...
or the consistent histories
Consistent histories
In quantum mechanics, the consistent histories approach is intended to give a modern interpretation of quantum mechanics, generalising the conventional Copenhagen interpretation and providing a natural interpretation of quantum cosmology...
interpretations.
In addition to the unpredictable and irreversible character of measurement processes, there are other elements of quantum physics that distinguish it sharply from classical physics and which are not present in any classical theory. One of these is the phenomenon of entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
, as illustrated in the EPR paradox
EPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
, which seemingly violates
Action at a distance (physics)
In physics, action at a distance is the interaction of two objects which are separated in space with no known mediator of the interaction. This term was used most often in the context of early theories of gravity and electromagnetism to describe how an object responds to the influence of distant...
principles of local causality
Principle of locality
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
.
Another obstruction to interpretation is the phenomenon of complementarity
Complementarity (physics)
In physics, complementarity is a basic principle of quantum theory proposed by Niels Bohr, closely identified with the Copenhagen interpretation, and refers to effects such as the wave–particle duality...
, which seems to violate basic principles of propositional logic
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
. Complementarity says there is no logical picture (one obeying classical propositional logic) that can simultaneously describe and be used to reason about all properties of a quantum system S. This is often phrased by saying that there are "complementary" propositions A and B that can each describe S, but not at the same time. Examples of A and B are propositions using a wave description of S and a corpuscular description of S. The latter statement is one part of Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
's original formulation, which is often equated to the principle of complementarity itself.
Complementarity does not usually imply that it is classical logic which is at fault (although Hilary Putnam
Hilary Putnam
Hilary Whitehall Putnam is an American philosopher, mathematician and computer scientist, who has been a central figure in analytic philosophy since the 1960s, especially in philosophy of mind, philosophy of language, philosophy of mathematics, and philosophy of science...
did take that view in his paper "Is logic empirical?
Is logic empirical?
"Is logic empirical?" is the title of two articles that discuss the idea that the algebraic properties of logic may, or should, be empirically determined; in particular, they deal with the question of whether empirical facts about quantum phenomena may provide grounds for revising classical logic...
"). Rather, complementarity means that the composition of physical properties for S (such as position and momentum both having values within certain ranges), using propositional connectives, does not obey the rules of classical propositional logic (see also Quantum logic
Quantum logic
In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...
). As is now well-known (Omnès, 1999) the "origin of complementarity lies in the non-commutativity of [the] operators" that describe observables (i.e., particles) in quantum mechanics.
Because the complexity of a quantum system is exponential in its number of degrees of freedom, it is difficult to overlap the quantum and classical descriptions to see how the classical approximations are being made.
Problematic status of interpretations
As classical physics and non-mathematical languageLanguage
Language may refer either to the specifically human capacity for acquiring and using complex systems of communication, or to a specific instance of such a system of complex communication...
cannot match the precision of quantum mechanics mathematics, anything said outside the mathematical formulation is necessarily limited in accuracy.
Also, the precise ontological status of each interpretation remains a matter of philosophical argument. In other words, if we interpret the formal structure X of quantum mechanics by means of a structure Y (via a mathematical equivalence of the two structures), what is the status of Y? This is the old question of saving the phenomena
Scientific formalism
Scientific formalism is a broad term for a family of approaches to the presentation of science. It is viewed as an important part of the scientific method, especially in the physical sciences.-Levels of formalism:...
, in a new guise.
Some physicists, for example Asher Peres
Asher Peres
Asher Peres was an Israeli physicist, considered a pioneer in quantum information theory. According to his autobiography, he was born in Beaulieu-sur-Dordogne in France, where his father, a Polish electrical engineer, had found work laying down power lines...
and Chris Fuchs, argue that an interpretation is nothing more than a formal equivalence between sets of rules for operating on experimental data, thereby implying that the whole exercise of interpretation is unnecessary.
Instrumentalist interpretation
Any modern scientific theory requires at the very least an instrumentalist description that relates the mathematical formalism to experimental practice and prediction. In the case of quantum mechanics, the most common instrumentalist description is an assertion of statistical regularity between state preparation processes and measurement processes. That is, if a measurement of a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-value quantity is performed many times, each time starting with the same initial conditions, the outcome is a well-defined probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
agreeing with the real numbers; moreover, quantum mechanics provides a computational instrument to determine statistical properties of this distribution, such as its expectation value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
Calculations for measurements performed on a system S postulate a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H over the complex numbers. When the system S is prepared in a pure state, it is associated with a vector in H. Measurable quantities are associated with Hermitian operators acting on H: these are referred to as observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s.
Repeated measurement of an observable A where S is prepared in state ψ yields a distribution of values. The expectation value of this distribution is given by the expression
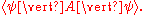
This mathematical machinery gives a simple, direct way to compute a statistical property of the outcome of an experiment, once it is understood how to associate the initial state with a Hilbert space vector, and the measured quantity with an observable (that is, a specific Hermitian operator).
As an example of such a computation, the probability of finding the system in a given state
 is given by computing the expectation value of a (rank-1) projection operator
is given by computing the expectation value of a (rank-1) projection operator
The probability is then the non-negative real number given by
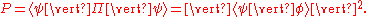
By abuse of language, a bare instrumentalist description could be referred to as an interpretation, although this usage is somewhat misleading since instrumentalism explicitly avoids any explanatory role; that is, it does not attempt to answer the question why.
Classification adopted by Einstein
An interpretation (i.e. a semantic explanationSemantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
of the formal mathematics of quantum mechanics) can be characterized by its treatment of certain matters addressed by Einstein, such as:
- Realism
- Completeness
- Local realismPrinciple of localityIn physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
- DeterminismDeterminismDeterminism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
To explain these properties, we need to be more explicit about the kind of picture an interpretation provides. To that end we will regard an interpretation as a correspondence between the elements of the mathematical formalism M and the elements of an interpreting structure I, where:
- The mathematical formalism M consists of the Hilbert space machinery of ket-vectorsBra-ket notationBra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
, self-adjoint operatorSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s acting on the space of ket-vectors, unitary time dependence of the ket-vectors, and measurement operations. In this context a measurement operation is a transformation which turns a ket-vector into a probability distribution (for a formalization of this concept see quantum operationQuantum operationIn quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
s). - The interpreting structure I includes states, transitions between states, measurement operations, and possibly information about spatial extension of these elements. A measurement operation refers to an operation which returns a value and might result in a system state change. Spatial information would be exhibited by states represented as functions on configuration space. The transitions may be non-deterministicQuantum indeterminacyQuantum indeterminacy is the apparent necessary incompleteness in the description of a physical system, that has become one of the characteristics of the standard description of quantum physics...
or probabilistic or there may be infinitely many states.
The crucial aspect of an interpretation is whether the elements of I are regarded as physically real. Hence the bare instrumentalist view of quantum mechanics outlined in the previous section is not an interpretation at all, for it makes no claims about elements of physical reality.
The current usage of realism and completeness originated in the 1935 paper in which Einstein and others proposed the EPR paradox
EPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
. In that paper the authors proposed the concepts element of reality and the completeness of a physical theory. They characterised element of reality as a quantity whose value can be predicted with certainty before measuring or otherwise disturbing it, and defined a complete physical theory as one in which every element of physical reality is accounted for by the theory. In a semantic view of interpretation, an interpretation is complete if every element of the interpreting structure is present in the mathematics. Realism is also a property of each of the elements of the maths; an element is real if it corresponds to something in the interpreting structure. For example, in some interpretations of quantum mechanics (such as the many-worlds interpretation) the ket vector associated to the system state is said to correspond to an element of physical reality, while in other interpretations it is not.
Determinism is a property characterizing state changes due to the passage of time, namely that the state at a future instant is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the state in the present (see time evolution
Time evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...
). It may not always be clear whether a particular interpretation is deterministic or not, as there may not be a clear choice of a time parameter. Moreover, a given theory may have two interpretations, one of which is deterministic and the other not.
Local realism has two aspects:
- The value returned by a measurement corresponds to the value of some function in the state space. In other words, that value is an element of reality;
- The effects of measurement have a propagation speed not exceeding some universal limit (e.g. the speed of light). In order for this to make sense, measurement operations in the interpreting structure must be localized.
A precise formulation of local realism in terms of a local hidden variable theory
Local hidden variable theory
In quantum mechanics, a local hidden variable theory is one in which distant events are assumed to have no instantaneous effect on local ones....
was proposed by John Bell
John Stewart Bell
John Stewart Bell FRS was a British physicist from Northern Ireland , and the originator of Bell's theorem, a significant theorem in quantum physics regarding hidden variable theories.- Early life and work :...
.
Bell's theorem
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
, combined with experimental testing, restricts the kinds of properties a quantum theory can have. For instance, Bell's theorem implies that quantum mechanics cannot satisfy local realism.
The Copenhagen interpretation
The Copenhagen interpretationCopenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
is the "standard" interpretation of quantum mechanics formulated by Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
and Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
while collaborating in Copenhagen around 1927. Bohr and Heisenberg extended the probabilistic interpretation of the wavefunction proposed originally by Max Born. The Copenhagen interpretation rejects questions like "where was the particle before I measured its position?" as meaningless. The measurement process randomly picks out exactly one of the many possibilities allowed for by the state's wave function in a manner consistent with the well-defined probabilities that are assigned to each possible state. According to the interpretation, the interaction of an observer or apparatus that is external to the quantum system is the cause of wave function collapse, thus according to Heisenberg "reality is in the observations, not in the electron".
Many worlds
The many-worlds interpretationMany-worlds interpretation
The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...
is an interpretation of quantum mechanics in which a universal wavefunction
Universal wavefunction
The Universal Wavefunction or Universal Wave Function is a term introduced by Hugh Everett in his Princeton PhD thesis The Theory of the Universal Wave Function, and forms a core concept in the relative state interpretation or many-worlds interpretation of quantum mechanics...
obeys the same deterministic, reversible
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
laws at all times; in particular there is no (indeterministic and irreversible
Irreversibility
In science, a process that is not reversible is called irreversible. This concept arises most frequently in thermodynamics, as applied to processes....
) wavefunction collapse
Wavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
associated with measurement. The phenomena associated with measurement are claimed to be explained by decoherence
Quantum decoherence
In quantum mechanics, quantum decoherence is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition. A consequence of this dephasing leads to classical or probabilistically additive behavior...
, which occurs when states interact with the environment producing entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
, repeatedly splitting the universe into mutually unobservable alternate histories—distinct universes within a greater multiverse
Multiverse (science)
The multiverse is the hypothetical set of multiple possible universes that together comprise everything that exists and can exist: the entirety of space, time, matter, and energy as well as the physical laws and constants that describe them...
.
Consistent histories
The consistent historiesConsistent histories
In quantum mechanics, the consistent histories approach is intended to give a modern interpretation of quantum mechanics, generalising the conventional Copenhagen interpretation and providing a natural interpretation of quantum cosmology...
interpretation generalizes the conventional Copenhagen interpretation and attempts to provide a natural interpretation of quantum cosmology
Quantum cosmology
In theoretical physics, quantum cosmology is a field attempting to study the effect of quantum mechanics on the formation of the universe, or its early evolution, especially just after the Big Bang...
. The theory is based on a consistency criterion that allows the history of a system to be described so that the probabilities for each history obey the additive rules of classical probability. It is claimed to be consistent with the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
.
According to this interpretation, the purpose of a quantum-mechanical theory is to predict the relative probabilities of various alternative histories (for example, of a particle).
Ensemble interpretation, or statistical interpretation
The Ensemble interpretationEnsemble Interpretation
The ensemble interpretation, or statistical interpretation of quantum mechanics, is an interpretation that can be viewed as a minimalist interpretation; it is a quantum mechanical interpretation that claims to make the fewest assumptions associated with the standard mathematical formalization...
, also called the statistical interpretation, can be viewed as a minimalist interpretation. That is, it claims to make the fewest assumptions associated with the standard mathematics. It takes the statistical interpretation of Born to the fullest extent. The interpretation states that the wave function does not apply to an individual system for example, a single particle but is an abstract statistical quantity that only applies to an ensemble (a vast multitude) of similarly prepared systems or particles. Probably the most notable supporter of such an interpretation was Einstein:
The most prominent current advocate of the ensemble interpretation is Leslie E. Ballentine, Professor at Simon Fraser University
Simon Fraser University
Simon Fraser University is a Canadian public research university in British Columbia with its main campus on Burnaby Mountain in Burnaby, and satellite campuses in Vancouver and Surrey. The main campus in Burnaby, located from downtown Vancouver, was established in 1965 and has more than 34,000...
, author of the graduate level text book Quantum Mechanics, A Modern Development. An experiment illustrating the ensemble interpretation is provided in Akira Tonomura's Video clip 1
. It is evident from this double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
with an ensemble of individual electrons that, since the quantum mechanical wave function (absolutely squared) describes the completed interference pattern, it must describe an ensemble.
de Broglie–Bohm theory
The de Broglie–Bohm theory of quantum mechanics is a theory by Louis de Broglie and extended later by David BohmDavid Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
to include measurements. Particles, which always have positions, are guided by the wavefunction. The wavefunction evolves according to the Schrödinger wave equation, and the wavefunction never collapses. The theory takes place in a single space-time, is non-local
Action at a distance (physics)
In physics, action at a distance is the interaction of two objects which are separated in space with no known mediator of the interaction. This term was used most often in the context of early theories of gravity and electromagnetism to describe how an object responds to the influence of distant...
, and is deterministic. The simultaneous determination of a particle's position and velocity is subject to the usual uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
constraint. The theory is considered to be a hidden variable theory
Hidden variable theory
Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation...
, and by embracing non-locality it satisfies Bell's inequality. The measurement problem
Measurement problem
The measurement problem in quantum mechanics is the unresolved problem of how wavefunction collapse occurs. The inability to observe this process directly has given rise to different interpretations of quantum mechanics, and poses a key set of questions that each interpretation must answer...
is resolved, since the particles have definite positions at all times. Collapse is explained as phenomenological.
Relational quantum mechanics
The essential idea behind relational quantum mechanicsRelational quantum mechanics
Relational quantum mechanics is an interpretation of quantum mechanics which treats the state of a quantum system as being observer-dependent, that is, the state is the relation between the observer and the system. This interpretation was first delineated by Carlo Rovelli in a 1994 preprint, and...
, following the precedent of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" eigenstate, while to another observer at the same time, it may be in a superposition of two or more states. Consequently, if quantum mechanics is to be a complete theory, relational quantum mechanics argues that the notion of "state" describes not the observed system itself, but the relationship, or correlation, between the system and its observer(s). The state vector
State vector
*A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of freedom for motion *A state vector in general control systems describes the observed states of an object in state space, e.g. in variables of the degrees of...
of conventional quantum mechanics becomes a description of the correlation of some degrees of freedom in the observer, with respect to the observed system. However, it is held by relational quantum mechanics that this applies to all physical objects, whether or not they are conscious or macroscopic. Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. Thus the physical content of the theory has to do not with objects themselves, but the relations between them.
An independent relational approach to quantum mechanics
Relational approach to quantum physics
The relational approach to quantum physics is an alternative approach to and interpretation of quantum mechanics. It asserts that the physical world can only be studied accurately in terms of relationships between systems, as all experimentally verifiable facts about the world result explicitly...
was developed in analogy with David Bohm's elucidation of special relativity, in which a detection event is regarded as establishing a relationship between the quantized field and the detector. The inherent ambiguity associated with applying Heisenberg's uncertainty principle is subsequently avoided.
Transactional interpretation
The transactional interpretationTransactional interpretation
The transactional interpretation of quantum mechanics describes quantum interactions in terms of a standing wave formed by retarded and advanced waves. It was first proposed in 1986 by John G...
of quantum mechanics (TIQM) by John G. Cramer
John G. Cramer
John G. Cramer is a professor of physics at the University of Washington in Seattle, the United States. When not teaching, he works with the STAR detector at the new Relativistic Heavy Ion Collider at Brookhaven National Laboratory, and the particle accelerator at CERN in Geneva, Switzerland...
is an interpretation of quantum mechanics inspired by the Wheeler–Feynman absorber theory. It describes quantum interactions in terms of a standing wave formed by retarded (forward-in-time) and advanced (backward-in-time) waves. The author argues that it avoids the philosophical problems with the Copenhagen interpretation and the role of the observer, and resolves various quantum paradoxes.
Stochastic mechanics
An entirely classical derivation and interpretation of Schrödinger's wave equation by analogy with Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
was suggested by Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
professor Edward Nelson
Edward Nelson
Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...
in 1966. Similar considerations had previously been published, for example by R. Fürth (1933), I. Fényes (1952), and Walter Weizel
Walter Weizel
Walter Friedrich Karl Weizel was a German theoretical physicist and politician. As a result of his opposition to National Socialism in Germany, he was forced into early retirement for a short duration in 1933. He was a full professor at the University of Bonn, from 1936 to 1969...
(1953), and are referenced in Nelson's paper. More recent work on the stochastic interpretation has been done by M. Pavon. An alternative stochastic interpretation was developed by Roumen Tsekov.
Objective collapse theories
Objective collapse theories differ from the Copenhagen interpretationCopenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
in regarding both the wavefunction and the process of collapse as ontologically objective. In objective theories, collapse occurs randomly ("spontaneous localization"), or when some physical threshold is reached, with observers having no special role. Thus, they are realistic, indeterministic, no-hidden-variables theories. The mechanism of collapse is not specified by standard quantum mechanics, which needs to be extended if this approach is correct, meaning that Objective Collapse is more of a theory than an interpretation. Examples include the Ghirardi-Rimini-Weber theory
Ghirardi-Rimini-Weber theory
The Ghirardi–Rimini–Weber theory, or GRW, is a collapse theory in quantum mechanics. GRW differs from other collapse theories by proposing that wave function collapse happens spontaneously. GRW is an attempt to avoid the measurement problem in quantum mechanics...
and the Penrose interpretation
Penrose interpretation
The Penrose interpretation is a prediction of Sir Roger Penrose about the relationship between quantum mechanics and general relativity. Penrose proposes that a quantum state remains in superposition until the difference of space-time curvature attains a significant level...
.
von Neumann/Wigner interpretation: consciousness causes the collapse
In his treatise The Mathematical Foundations of Quantum Mechanics, John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
deeply analyzed the so-called measurement problem
Measurement problem
The measurement problem in quantum mechanics is the unresolved problem of how wavefunction collapse occurs. The inability to observe this process directly has given rise to different interpretations of quantum mechanics, and poses a key set of questions that each interpretation must answer...
. He concluded that the entire physical universe could be made subject to the Schrödinger equation (the universal wave function). Since something "outside the calculation" was needed to collapse the wave function, von Neumann concluded that the collapse was caused by the consciousness of the experimenter. This point of view was later more prominently expanded on by Eugene Wigner, but remains a view held by very few physicists.
Variations of the von Neumann interpretation include:
- Subjective reduction research
- This principle, that consciousness causes the collapseQuantum mind/body problemThe quantum mind–body problem refers to the philosophical discussions of the mind–body problem in the context of quantum mechanics. Since quantum mechanics involves quantum superpositions, which are not perceived by observers, some interpretations of quantum mechanics place conscious observers in a...
, is the point of intersection between quantum mechanics and the mind/body problem; and researchers are working to detect conscious events correlated with physical events that, according to quantum theory, should involve a wave function collapse; but, thus far, results are inconclusive.
- This principle, that consciousness causes the collapse
- Participatory anthropic principle (PAP)
-
- John Archibald WheelerJohn Archibald WheelerJohn Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
's participatory anthropic principle says that consciousness plays some role in bringing the universe into existence.
- John Archibald Wheeler
Other physicists have elaborated their own variations of the von Neumann interpretation; including:
- Henry P. Stapp (Mindful Universe: Quantum Mechanics and the Participating Observer)
- Bruce Rosenblum and Fred Kuttner (Quantum Enigma: Physics Encounters Consciousness)
Many minds
The many-minds interpretation of quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
extends the many-worlds interpretation
Many-worlds interpretation
The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...
by proposing that the distinction between worlds should be made at the level of the mind of an individual observer.
Quantum logic
Quantum logicQuantum logic
In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...
can be regarded as a kind of propositional logic suitable for understanding the apparent anomalies regarding quantum measurement, most notably those concerning composition of measurement operations of complementary variables. This research area and its name originated in the 1936 paper by Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
and John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, who attempted to reconcile some of the apparent inconsistencies of classical boolean logic with the facts related to measurement and observation in quantum mechanics.
Quantum information theories
Informational approaches subdivide into two kinds- Information ontologies, such as J. A. Wheeler's "it from bit". These approaches have been described as a revival of immaterialismIdealismIn philosophy, idealism is the family of views which assert that reality, or reality as we can know it, is fundamentally mental, mentally constructed, or otherwise immaterial. Epistemologically, idealism manifests as a skepticism about the possibility of knowing any mind-independent thing...
- Interpretations where quantum mechanics is said to describe an observer's knowledge of the world, rather than the world itself. This approach has some similarity with Bohr's thinking. Collapse (also known as reduction) is often interpreted as an observer acquiring information from a measurement, rather than as an objective event. These approaches have been appraised as similar to instrumentalismInstrumentalismIn the philosophy of science, instrumentalism is the view that a scientific theory is a useful instrument in understanding the world. A concept or theory should be evaluated by how effectively it explains and predicts phenomena, as opposed to how accurately it describes objective...
.
The state is not an objective property of an individual system but is that
information, obtained from a knowledge of how a system was prepared, which
can be used for making predictions about future measurements.
...A quantum mechanical state being a summary of the observer’s information
about an individual physical system changes both by dynamical laws, and
whenever the observer acquires new information about the system through
the process of measurement. The existence of two laws for the evolution
of the state vector...becomes problematical only if it is believed that the
state vector is an objective property of the system...The “reduction of the
wavepacket” does take place in the consciousness of the observer, not because
of any unique physical process which takes place there, but only because the
state is a construct of the observer and not an objective property of the
physical system
Modal interpretations of quantum theory
Modal interpretations of quantum mechanics were first conceived of in 1972 by B. van Fraassen, in his paper “A formal approach to the philosophy of science.” However, this term now is used to describe a larger set of models that grew out of this approach. The Stanford Encyclopedia of PhilosophyStanford Encyclopedia of Philosophy
The Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
describes several versions:
- The Copenhagen variant
- Kochen-DieksDennis DieksDennis Dieks is a Dutch physicist and philosopher of physics. In 1982 he proved the no-cloning theorem . In 1989 he proposed a new interpretation of quantum mechanics, later known as a version of the modal interpretation of quantum mechanics...
-Healey Interpretations - Motivating Early Modal Interpretations, based on the work of R. Clifton, M. Dickson and J. Bub.
Time-symmetric theories
Several theories have been proposed which modify the equations of quantum mechanics to be symmetric with respect to time reversal. This creates retrocausalityRetrocausality
Retrocausality is any of several hypothetical phenomena or processes that reverse causality, allowing an effect to occur before its cause....
: events in the future can affect ones in the past, exactly as events in the past can affect ones in the future. In these theories, a single measurement cannot fully determine the state of a system (making them a type of hidden variables theory), but given two measurements performed at different times, it is possible to calculate the exact state of the system at all intermediate times. The collapse of the wavefunction is therefore not a physical change to the system, just a change in our knowledge of it due to the second measurement. Similarly, they explain entanglement as not being a true physical state but just an illusion created by ignoring retrocausality. The point where two particles appear to "become entangled" is simply a point where each particle is being influenced by events that occur to the other particle in the future.
Branching space-time theories
BST theories resemble the many worlds interpretation; however, "the main difference is that the BST interpretation takes the branching of history to be feature of the topology of the set of events with their causal relationships... rather than a consequence of the separate evolution of different components of a state vector." In MWI, it is the wave functions that branches, whereas in BST, the space-time topology itself branches.BST has applications to Bells theorem, quantum computation and quantum gravity. It also has some resemblance to hidden variable theories and the ensemble interpretation.: particles in BST have multiple well defined trajectories at the microscopic level. These can only be treated stochastically at a coarse grained level, in line
with the ensemble interpretation.
Other interpretations
As well as the mainstream interpretations discussed above, a number of other interpretations have been proposed which have not made a significant scientific impact. These range from proposals by mainstream physicists to the more occultOccult
The word occult comes from the Latin word occultus , referring to "knowledge of the hidden". In the medical sense it is used to refer to a structure or process that is hidden, e.g...
ideas of quantum mysticism
Quantum mysticism
Quantum mysticism is a term that has been used to refer to a set of metaphysical beliefs and associated practices that seek to relate consciousness, intelligence or mystical world-views to the ideas of quantum mechanics and its interpretations...
.
Comparison
The most common interpretations are summarized in the table below. The values shown in the cells of the table are not without controversy, for the precise meanings of some of the concepts involved are unclear and, in fact, are themselves at the center of the controversy surrounding the given interpretation.No experimental evidence exists that distinguishes among these interpretations. To that extent, the physical theory stands, and is consistent with itself and with reality; difficulties arise only when one attempts to "interpret" the theory. Nevertheless, designing experiments which would test the various interpretations is the subject of active research.
Most of these interpretations have variants. For example, it is difficult to get a precise definition of the Copenhagen interpretation as it was developed and argued about by many people.
| Interpretation | Author(s) | Deterministic? Determinism Determinism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and... |
Wavefunction real? |
Unique history? |
Hidden variables Hidden variable theory Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation... ? |
Collapsing wavefunctions? Wavefunction collapse In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer... |
Observer role? |
Local? | Counterfactual definiteness Counterfactual definiteness In some interpretations of quantum mechanics, counterfactual definiteness is the ability to speak with meaning of the definiteness of the results of measurements that have not been performed... ? |
|---|---|---|---|---|---|---|---|---|---|
| Ensemble interpretation Ensemble Interpretation The ensemble interpretation, or statistical interpretation of quantum mechanics, is an interpretation that can be viewed as a minimalist interpretation; it is a quantum mechanical interpretation that claims to make the fewest assumptions associated with the standard mathematical formalization... |
Max Born Max Born Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s... , 1926 |
Agnostic | No | Yes | Agnostic | No | None | No | No |
| Copenhagen interpretation | Niels Bohr Niels Bohr Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in... , Werner Heisenberg Werner Heisenberg Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory... , 1927 |
No | No | Yes | No | Yes | None | No | No |
| de Broglie-Bohm theory | Louis de Broglie, 1927, David Bohm David Bohm David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:... , 1952 |
Yes | Yes | Yes | Yes | No | None | No | Yes |
| von Neumann interpretation | von Neumann, 1932, Wheeler John Archibald Wheeler John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission... , Wigner |
No | Yes | Yes | No | Yes | Causal | No | No |
| Quantum logic Quantum logic In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account... |
Garrett Birkhoff Garrett Birkhoff Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father.... , 1936 |
Agnostic | Agnostic | Yes | No | No | Interpretational | Agnostic | No |
| Many-worlds interpretation Many-worlds interpretation The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an... |
Hugh Everett Hugh Everett Hugh Everett III was an American physicist who first proposed the many-worlds interpretation of quantum physics, which he termed his "relative state" formulation.... , 1957 |
Yes | Yes | No | No | No | None | Yes | No |
| Popper's interpretation Popper's experiment Popper's experiment is an experiment proposed by the 20th century philosopher of science Karl Popper, an advocate of an objective interpretation of quantum mechanics. He wanted to test the Copenhagen interpretation, a popular subjectivist interpretation of quantum mechanics... |
Karl Popper Karl Popper Sir Karl Raimund Popper, CH FRS FBA was an Austro-British philosopher and a professor at the London School of Economics... , 1957 |
No | Yes | Yes | Yes | No | None | Yes | Yes |
| Time-symmetric theories | Yakir Aharonov Yakir Aharonov Yakir Aharonov is an Israeli physicist specializing in quantum physics. He is a Professor of Theoretical Physics and the James J. Farley Professor of Natural Philosophy at Chapman University in California. He is also a distinguished professor in Perimeter Institute.He also serves as a professor... , 1964 |
Yes | Yes | Yes | Yes | No | No | Yes | No |
| Stochastic interpretation Stochastic interpretation The stochastic interpretation is an interpretation of quantum mechanics.The modern application of stochastics to quantum mechanics involves the assumption of spacetime stochasticity, the idea that the small-scale structure of spacetime is undergoing both metric and topological fluctuations , and... |
Edward Nelson Edward Nelson Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic... , 1966 |
No | No | Yes | No | No | None | No | No |
| Many-minds interpretation Many-minds interpretation The many-minds interpretation of quantum mechanics extends the many-worlds interpretation by proposing that the distinction between worlds should be made at the level of the mind of an individual observer. The concept was first introduced in 1970 by H... |
H. Dieter Zeh H. Dieter Zeh Heinz-Dieter Zeh , is a Professor Emeritus of the University of Heidelberg and theoretical physicist... , 1970 |
Yes | Yes | No | No | No | Interpretational | Yes | No |
| Consistent histories Consistent histories In quantum mechanics, the consistent histories approach is intended to give a modern interpretation of quantum mechanics, generalising the conventional Copenhagen interpretation and providing a natural interpretation of quantum cosmology... |
Robert B. Griffiths, 1984 | Agnostic | Agnostic | No | No | No | Interpretational | Yes | No |
| Objective collapse theories Objective collapse theory Objective collapse theories are an approach to the interpretational problems of quantum mechanics. They are realistic, indeterministic and reject hidden variables... |
Ghirardi-Rimini-Weber Ghirardi-Rimini-Weber theory The Ghirardi–Rimini–Weber theory, or GRW, is a collapse theory in quantum mechanics. GRW differs from other collapse theories by proposing that wave function collapse happens spontaneously. GRW is an attempt to avoid the measurement problem in quantum mechanics... , 1986 |
No | Yes | Yes | No | Yes | None | No | No |
| Transactional interpretation Transactional interpretation The transactional interpretation of quantum mechanics describes quantum interactions in terms of a standing wave formed by retarded and advanced waves. It was first proposed in 1986 by John G... |
John G. Cramer John G. Cramer John G. Cramer is a professor of physics at the University of Washington in Seattle, the United States. When not teaching, he works with the STAR detector at the new Relativistic Heavy Ion Collider at Brookhaven National Laboratory, and the particle accelerator at CERN in Geneva, Switzerland... , 1986 |
No | Yes | Yes | No | Yes | None | No | No |
| Relational interpretation Relational quantum mechanics Relational quantum mechanics is an interpretation of quantum mechanics which treats the state of a quantum system as being observer-dependent, that is, the state is the relation between the observer and the system. This interpretation was first delineated by Carlo Rovelli in a 1994 preprint, and... |
Carlo Rovelli Carlo Rovelli Carlo Rovelli is an Italian physicist who has worked in Italy, the USA, and France. His work is mainly in the field of quantum gravity. He is among the founders of the Loop Quantum Gravity theory.-Life and career:... , 1994 |
No | No | Agnostic | No | Yes | Intrinsic | Yes | No |
According to Bohr, the concept of a physical state independent of the conditions of its experimental observation does not have a well-defined meaning. According to Heisenberg the wavefunction represents a probability, but not an objective reality itself in space and time. According to the Copenhagen interpretation, the wavefunction collapses when a measurement is performed. Both particle AND guiding wavefunction are real. Unique particle history, but multiple wave histories. But quantum logic is more limited in applicability than Coherent Histories. Quantum mechanics is regarded as a way of predicting observations, or a theory of measurement. Observers separate the universal wavefunction into orthogonal sets of experiences. If wavefunction is real then this becomes the many-worlds interpretation. If wavefunction less than real, but more than just information, then Zurek calls this the "existential interpretation". In the TI the collapse of the state vector is interpreted as the completion of the transaction between emitter and absorber. Comparing histories between systems in this interpretation has no well-defined meaning. Any physical interaction is treated as a collapse event relative to the systems involved, not just macroscopic or conscious observers. The state of the system is observer-dependent, i.e., the state is specific to the reference frame of the observer. Caused by the fact that Popper holds both CFD and locality to be true, it is under dispute whether Popper's interpretation can really be considered an interpretation of Quantum Mechanics (which is what Popper claimed) or whether it must be considered a modification of Quantum Mechanics (which is what many Physicists claim), and, in case of the latter, if this modification has been empirically refuted or not. Popper exchanged many long letters with Einstein, Bell etc. about the issue.
See also
- Glossary of quantum philosophyGlossary of quantum philosophyThis is a glossary for the terminology applied in the foundations of quantum mechanics and quantum metaphysics , a subfield of philosophy of physics....
- Afshar experimentAfshar experimentThe Afshar experiment is an optical experiment, devised and carried out by Shahriar Afshar in 2001, which investigates the principle of complementarity in quantum mechanics...
- Bohr–Einstein debatesBohr–Einstein debatesThe Bohr–Einstein debates were a series of public disputes about quantum mechanics between Albert Einstein and Niels Bohr, who were two of its founders. Their debates are remembered because of their importance to the philosophy of science. An account of them has been written by Bohr in an article...
- Path integral formulationPath integral formulationThe path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
- Philosophical interpretation of classical physicsPhilosophical interpretation of classical physicsClassical Newtonian physics has, formally, been replaced by quantum mechanics on the small scale and relativity on the large scale. Because most humans continue to think in terms of the kind of events we perceive in the human scale of daily life, it became necessary to provide a new philosophical...
- Quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
- Quantum Zeno effectQuantum Zeno effectThe quantum Zeno effect is a name coined by George Sudarshan and Baidyanath Misra of the University of Texas in 1977 in their analysis of the situation in which an unstable particle, if observed continuously, will never decay. One can nearly "freeze" the evolution of the system by measuring it...
Sources
- Bub, J. and Clifton, R. 1996. “A uniqueness theorem for interpretations of quantum mechanics,” Studies in History and Philosophy of Modern Physics 27B: 181-219
- Rudolf CarnapRudolf CarnapRudolf Carnap was an influential German-born philosopher who was active in Europe before 1935 and in the United States thereafter. He was a major member of the Vienna Circle and an advocate of logical positivism....
, 1939, "The interpretation of physics," in Foundations of Logic and Mathematics of the International Encyclopedia of Unified ScienceInternational Encyclopedia of Unified ScienceIn 1938 a new series of publications started in USA. It was the International Encyclopedia of Unified Science . An ambitious project never completed devoted to unified science...
. University of Chicago Press. - Dickson, M., 1994, "Wavefunction tails in the modal interpretation" in Hull, D., Forbes, M., and Burian, R., eds., Proceedings of the PSA 1" 366–76. East Lansing, Michigan: Philosophy of Science Association.
- --------, and Clifton, R., 1998, "Lorentz-invariance in modal interpretations" in Dieks, D. and Vermaas, P., eds., The Modal Interpretation of Quantum Mechanics. Dordrecht: Kluwer Academic Publishers: 9–48.
- Fuchs, Christopher, 2002, "Quantum Mechanics as Quantum Information (and only a little more)."
- -------- and A. Peres, 2000, "Quantum theory needs no ‘interpretation’," Physics Today.
- Herbert, N., 1985. Quantum Reality: Beyond the New Physics. New York: Doubleday. ISBN 0-385-23569-0.
- Hey, Anthony, and Walters, P., 2003. The New Quantum Universe, 2nd ed. Cambridge Univ. Press. ISBN 0-5215-6457-3.
- Roman JackiwRoman JackiwRoman W. Jackiw is a theoretical physicist and Dirac Medallist. Born in Poland, Jackiw received his PhD from Cornell University in 1966 under Hans Bethe and Kenneth Wilson...
and D. Kleppner, 2000, "One Hundred Years of Quantum Physics," ScienceScienceScience is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
289(5481): 893. - Max Jammer, 1966. The Conceptual Development of Quantum Mechanics. McGraw-Hill.
- --------, 1974. The Philosophy of Quantum Mechanics. Wiley & Sons.
- Al-Khalili, 2003. Quantum: A Guide for the Perplexed. London: Weidenfeld & Nicholson.
- de Muynck, W. M., 2002. Foundations of quantum mechanics, an empiricist approach. Dordrecht: Kluwer Academic Publishers. ISBN 1-4020-0932-1.
- Roland OmnèsRoland OmnèsRoland Omnès is the author of several books which aim to close the gap between our common sense experience of the classical world and the complex, formal mathematics which is now required to accurately describe reality at its most fundamental level.- Biography :Omnès is currently Professor...
, 1999. Understanding Quantum Mechanics. Princeton Univ. Press. - Karl PopperKarl PopperSir Karl Raimund Popper, CH FRS FBA was an Austro-British philosopher and a professor at the London School of Economics...
, 1963. Conjectures and Refutations. London: Routledge and Kegan Paul. The chapter "Three views Concerning Human Knowledge" addresses, among other things, instrumentalism in the physical sciences. - Hans ReichenbachHans ReichenbachHans Reichenbach was a leading philosopher of science, educator and proponent of logical empiricism...
, 1944. Philosophic Foundations of Quantum Mechanics. Univ. of California Press. - Max TegmarkMax TegmarkMax Tegmark is a Swedish-American cosmologist. Tegmark is a professor at the Massachusetts Institute of Technology and belongs to the scientific directorate of the Foundational Questions Institute.-Early life:...
and J. A. Wheeler, 2001, "100 Years of Quantum Mysteries," Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
284: 68. - Bas van Fraassen, 1972, "A formal approach to the philosophy of science," in R. Colodny, ed., Paradigms and Paradoxes: The Philosophical Challenge of the Quantum Domain. Univ. of Pittsburgh Press: 303-66.
- John A. Wheeler and Wojciech Hubert Zurek (eds), Quantum Theory and Measurement, Princeton: Princeton University Press, ISBN 0-691-08316-9, LoC QC174.125.Q38 1983.
Further reading
Almost all authors below are professional physicists.- David Z Albert, 1992. Quantum Mechanics and Experience. Harvard Univ. Press. ISBN 0674741129.
- John S. Bell, 1987. Speakable and Unspeakable in Quantum Mechanics. Cambridge Univ. Press, ISBN 0-521-36869-3. The 2004 edition (ISBN 0-521-52338-9) includes two additional papers and an introduction by Alain AspectAlain AspectAlain Aspect is a French physicist noted for his experimental work on quantum entanglement....
. - Dmitrii Ivanovich Blokhintsev, 1968. The Philosophy of Quantum Mechanics. D. Reidel Publishing Company. ISBN 9027701059.
- David BohmDavid BohmDavid Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
, 1980. Wholeness and the Implicate Order. London: Routledge. ISBN 0-7100-0971-2. - David DeutschDavid DeutschDavid Elieser Deutsch, FRS is an Israeli-British physicist at the University of Oxford. He is a non-stipendiary Visiting Professor in the Department of Atomic and Laser Physics at the Centre for Quantum Computation in the Clarendon Laboratory of the University of Oxford...
, 1997. The Fabric of RealityThe Fabric of RealityThe Fabric of Reality is a book by physicist David Deutsch written in 1997. It expands upon his views of quantum mechanics and its implications for understanding reality....
. London: Allen Lane. ISBN 014027541X; ISBN 0713990619. Argues forcefully against instrumentalism. For general readers. - Bernard d'EspagnatBernard d'EspagnatBernard d'Espagnat is a French theoretical physicist, philosopher of science, and author, best known for his work on the nature of reality....
, 1976. Conceptual Foundation of Quantum Mechanics, 2nd ed. Addison Wesley. ISBN 081334087X. - --------, 1983. In Search of Reality. Springer. ISBN 0387113991.
- --------, 2003. Veiled Reality: An Analysis of Quantum Mechanical Concepts. Westview Press.
- --------, 2006. On Physics and Philosophy. Princeton Univ. Press.
- Arthur FineArthur FineArthur Fine is an American philosopher of science teaching at the University of Washington . Before moving to UW he taught for many years at Northwestern University and, before that, at Cornell University and the University of Illinois at Chicago...
, 1986. The Shaky Game: Einstein Realism and the Quantum Theory. Science and its Conceptual Foundations. Univ. of Chicago Press. ISBN 0226249484. - Ghirardi, Giancarlo, 2004. Sneaking a Look at God’s Cards. Princeton Univ. Press.
- Gregg Jaeger (2009) Entanglement, Information, and the Interpretation of Quantum Mechanics. Springer. ISBN 9783540921271.
- N. David Mermin (1990) Boojums all the way through. Cambridge Univ. Press. ISBN 0521388805.
- Roland OmnesRoland OmnèsRoland Omnès is the author of several books which aim to close the gap between our common sense experience of the classical world and the complex, formal mathematics which is now required to accurately describe reality at its most fundamental level.- Biography :Omnès is currently Professor...
, 1994. The Interpretation of Quantum Mechanics. Princeton Univ. Press. ISBN 0691036691. - --------, 1999. Understanding Quantum Mechanics. Princeton Univ. Press.
- --------, 1999. Quantum PhilosophyQuantum Philosophy (book)Quantum Philosophy is a book by the physicist Roland Omnès, in which he aims to show the non-specialist reader how modern developments in quantum mechanics allow the recovery of our common sense view of the world.- Book contents :...
: Understanding and Interpreting Contemporary Science. Princeton Univ. Press. - Roger PenroseRoger PenroseSir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
, 1989. The Emperor's New MindThe Emperor's New MindThe Emperor's New Mind: Concerning Computers, Minds and The Laws of Physics is a 1989 book by mathematical physicist Sir Roger Penrose.Penrose presents the argument that human consciousness is non-algorithmic, and thus is not capable of being modeled by a conventional Turing machine-type of digital...
. Oxford Univ. Press. ISBN 0-198-51973-7. Especially chpt. 6. - --------, 1994. Shadows of the MindShadows of the MindShadows of the Mind: A Search for the Missing Science of Consciousness is a 1994 book by mathematical physicist Roger Penrose, and serves as a followup to his 1989 book The Emperor's New Mind: Concerning Computers, Minds and The Laws of Physics....
. Oxford Univ. Press. ISBN 0-19-853978-9. - --------, 2004. The Road to Reality. New York: Alfred A. Knopf. Argues that quantum theory is incomplete.
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
:- "Bohmian mechanics" by Sheldon Goldstein.
- "Collapse Theories." by Giancarlo Ghirardi.
- "Copenhagen Interpretation of Quantum Mechanics" by Jan Faye.
- "Everett's Relative State Formulation of Quantum Mechanics" by Jeffrey Barrett.
- "Many-Worlds Interpretation of Quantum Mechanics" by Lev Vaidman.
- "Modal Interpretation of Quantum Mechanics" by Michael Dickson and Dennis Dieks.
- "Quantum Entanglement and Information" by Jeffrey BubJeffrey BubJeffrey Bub, born 1942, is a physicist and philosopher of science, and Distinguished Professor at the Committee for Philosophy and the Sciences, the Department of Philosophy and the Institute for Physical Science and Technology at the University of Maryland, College Park...
. - "Quantum mechanics" by Jenann Ismael.
- "Relational Quantum Mechanics" by Federico Laudisa and Carlo RovelliCarlo RovelliCarlo Rovelli is an Italian physicist who has worked in Italy, the USA, and France. His work is mainly in the field of quantum gravity. He is among the founders of the Loop Quantum Gravity theory.-Life and career:...
. - "The Role of Decoherence in Quantum Mechanics" by Guido Bacciagaluppi.
- Willem M. de Muynck, Broad overview of the realist vs. empiricist interpretations, against oversimplified view of the measurement process.
- Schreiber, Z., "The Nine Lives of Schrodinger's Cat." Overview of competing interpretations.
- Interpretations of quantum mechanics on arxiv.org.
- The many worlds of quantum mechanics.
- Erich Joos' Decoherence Website.
- Quantum Mechanics for Philosophers. Argues for the superiority of the Bohm interpretation.
- Hidden Variables in Quantum Theory: The Hidden Cultural Variables of their Rejection.
- Numerous Many Worlds-related Topics and Articles.
- Relational Approach to Quantum Physics.
- Theory of incomplete measurements. Deriving quantum mechanics axioms from properties of acceptable measurements.
- Alfred Neumaier's FAQ.
- Measurement in Quantum Mechanics FAQ.

