Projective space - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

a projective space is a set of elements similar to the set P(V) of lines through the origin of a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

V. The cases when V=R² or V=R³ are the projective line

Projective line

In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...

and the projective plane

Projective plane

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

, respectively.

The idea of a projective space relates to perspective

Perspective (graphical)

Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...

, more precisely to the way an eye or a camera projects a 3D scene to a 2D image. All points which lie on a projection line (i.e., a "line-of-sight"), intersecting with the focal point of the camera

Pinhole camera model

The pinhole camera model describes the mathematical relationship between the coordinates of a 3D point and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light...

, are projected onto a common image point. In this case the vector space is R³ with the camera focal point at the origin and the projective space corresponds to the image points.

Projective spaces can be studied as a separate field in mathematics, but are also used in various applied fields, geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

in particular. Geometric objects, such as points, lines, or planes, can be given a representation as elements in projective spaces based on homogeneous coordinates

Homogeneous coordinates

In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...

. As a result, various relations between these objects can be described in a simpler way than is possible without homogeneous coordinates. Furthermore, various statements in geometry can be made more consistent and without exceptions. For example, in the standard geometry for the plane two lines always intersect at a point except when the lines are parallel. In a projective representation of lines and points, however, such an intersection point exists even for parallel lines, and it can be computed in the same way as other intersection points.

Other mathematical fields where projective spaces play a significant role are topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, the theory of Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

s and algebraic group

Algebraic group

In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...

s, and their representation theories.

Introduction

As outlined above, projective space is a geometric object which formalizes statements like "Parallel lines intersect at infinity". For concreteness, we will give the construction of the real projective plane

Real projective plane

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...

P²(R) in some detail.
There are three equivalent definitions:

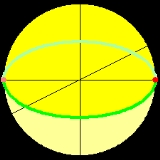
The set of all lines in R³ passing through the origin (0, 0, 0). Every such line meets the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

of radius one centered in the origin exactly twice, say in P = (x, y, z) and its antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....

(-x, -y, -z).
P²(R) can also be described to be the points on the sphere S², where every point P and its antipodal point are not distinguished. For example, the point (1, 0, 0) (red point in the image) is identified with (-1, 0, 0) (light red point), etc.
Finally, yet another equivalent definition is the set of equivalence classes of R³\(0, 0, 0), i.e. 3-space without the origin, where two points P = (x, y, z) and P* = (x*, y*, z*) are equivalent iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...

there is a nonzero real number λ such that P = λ·P*, i.e. x = λx*, y = λy*, z = λz*. The usual way to write an element of the projective plane, i.e. the equivalence class corresponding to an honest point (x, y, z) in R³, is: [x : y : z].

The last formula goes under the name of homogeneous coordinates

Homogeneous coordinates

.

Notice that any point [x : y : z] with z ≠ 0 is equivalent to [x/z : y/z : 1]. So there are two disjoint subsets of the projective plane: that consisting of the points [x : y : z] = [x/z : y/z : 1] for z ≠ 0, and that consisting of the remaining points [x : y : 0]. The latter set can be subdivided similarly into two disjoint subsets, with points [x/y : 1 : 0] and [x : 0 : 0]. In the last case, x is necessarily nonzero, because the origin was not part of P²(R). Thus the point is equivalent to [1 : 0 : 0]. Geometrically, the first subset, which is isomorphic (not only as a set, but also as a manifold, as will be seen later) to R², is in the image the yellow upper hemisphere (without the equator), or equivalently the lower hemisphere. The second subset, isomorphic to R¹, corresponds to the green line (without the two marked points), or, again, equivalently the light green
line. Finally we have the red point or the equivalent light red point. We thus have a disjoint decomposition

P²(R) = R² ⊔ R¹ ⊔ point.

Intuitively, and made precise below, R¹ ⊔ point is itself the real projective line P¹(R). Considered as a subset of P²(R), it is called line at infinity, whereas R² ⊂ P²(R) is called affine plane, i.e. just the usual plane.

The next objective is to make the saying "parallel lines meet at infinity" precise. A natural bijection between the plane z = 1 (which meets the sphere at the north pole

North Pole

The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is, subject to the caveats explained below, defined as the point in the northern hemisphere where the Earth's axis of rotation meets its surface...

N = (0, 0, 1)) and the affine plane inside the projective plane (i.e. the upper hemisphere) is accomplished by the stereographic projection

Stereographic projection

The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...

, i.e. any point P on this plane is mapped to the intersection point of the line through the origin and P and the sphere. Therefore two lines L₁ and L₂ (blue) in the plane are mapped to what looks like great circles (antipodal points are identified, though). Great circles intersect precisely in two antipodal points, which are identified in the projective plane, i.e. any two lines have exactly one intersection point inside P²(R). This phenomenon is axiomatized and studied in projective geometry

Projective geometry

In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...

Definition of projective space

Real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...

, Pⁿ (R), is defined by

Pⁿ(R) := (Rⁿ⁺¹ \ {0}) / ~,

with the equivalence relation (x₀, ..., x_n) ~ (λx₀, ..., λx_n), where λ is an arbitrary non-zero real number. Equivalently, it is the set of all lines in Rⁿ⁺¹ passing through the origin 0 := (0, ..., 0).

Instead of R, one may take any field, or even a division ring

Division ring

In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...

, k. Taking the complex numbers or the quaternions, one obtains the complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...

Pⁿ(C) and quaternionic projective space
Quaternionic projective space
In mathematics, quaternionic projective space is an extension of the ideas of real projective space and complex projective space, to the case where coordinates lie in the ring of quaternions H. Quaternionic projective space of dimension n is usually denoted byand is a closed manifold of dimension 4n...

Pⁿ(H).

If n is one or two, it is also called projective line

Projective line

or projective plane

Projective plane

, respectively. The complex projective line is also called the Riemann sphere

Riemann sphere

In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...

.

As in the above special case, the notation (so-called homogeneous coordinates

Homogeneous coordinates

) for a point in projective space is

[x₀ : ... : x_n].

Slightly more generally, for a vector space

Vector space

V (over some field k, or even more generally a module V over some division ring), P(V) is defined to be (V \ {0}) / ~, where two non-zero vectors v₁, v₂ in V are equivalent if they differ by a non-zero scalar λ, i.e., v₁ = λv₂. The vector space need not be finite-dimensional; thus, for example, there is the theory of projective Hilbert space

Projective Hilbert space

In mathematics and the foundations of quantum mechanics, the projective Hilbert space P of a complex Hilbert space H is the set of equivalence classes of vectors v in H, with v ≠ 0, for the relation given by...

Projective space as a manifold

The above definition of projective space gives a set. For purposes of differential geometry, which deals with manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

s, it is useful to endow this set with a (real or complex) manifold structure.

Namely consider the following subsets:

.
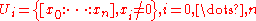By the definition of projective space, their union is the whole projective space. Furthermore, U_i is in bijection with Rⁿ (or Cⁿ) via the following maps:

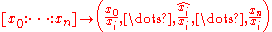
(the hat means that the i-th entry is missing).

The example image shows P¹(R). (Antipodal points are identified in P¹(R), though). It is covered by two copies of the real line R, each of which covers the projective line except one point, which is "the" (or a) point at infinity.

We first define a topology

Topology

on projective space by declaring that these maps shall be homeomorphisms, that is, a subset of U_i is open iff

IFF

IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...

its image under the above isomorphism is an open subset (in the usual sense) of Rⁿ. An arbitrary subset A of Pⁿ(R) is open if all intersections A ∩ U_i are open. This defines a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

.

The manifold structure is given by the above maps, too.
Another way to think about the projective line is the following: take two copies of the affine line with coordinates x and y, respectively, and glue them together along the subsets x ≠ 0 and y ≠ 0 via the maps

The resulting manifold is the projective line. The charts given by this construction are the same as the ones above. Similar presentations exist for higher-dimensional projective spaces.

The above decomposition in disjoint subsets reads in this generality:

Pⁿ(R) = Rⁿ ⊔ R^n-1 ⊔

⊔ R¹ ⊔ R⁰,

this so-called cell-decomposition can be used to calculate the singular cohomology of projective space.

All of the above holds for complex projective space, too. The complex projective line

Projective line

P¹(C) is an example of a Riemann surface

Riemann surface

In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...

Projective spaces in algebraic geometry

The covering by the above open subsets also shows that projective space is an algebraic variety

Algebraic variety

In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...

(or scheme

Scheme (mathematics)

In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...

), it is covered by n + 1 affine n-spaces. The construction of projective scheme is an instance of the Proj construction

Proj construction

In algebraic geometry, Proj is a construction analogous to the spectrum-of-a-ring construction of affine schemes, which produces objects with the typical properties of projective spaces and projective varieties...

Projective spaces in algebraic topology

Real projective n-space has a quite straightforward CW complex

CW complex

In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...

structure. That is, each n-dimensional real projective space has only one n-dimensional cell.

Projective space and affine space

There are some advantages of the projective space against affine space

Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...

(e.g. Pⁿ(R) vs. Aⁿ(R)). For these reasons it is important to know when a given manifold or variety is projective, i.e. embeds into (is a closed subset of) projective space. (Very) ample line bundles

Ample line bundle

In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...

are designed to tackle this question.

Note that a projective space can be formed by the projectivization of a vector space, as lines through the origin, but cannot be formed from an affine space without a choice of basepoint. That is, affine spaces are open subspaces of projective spaces, which are quotients of vector spaces.

Projective space is a compact topological space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

, affine space is not. Therefore, Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...

applies to show that every holomorphic function on Pⁿ(C) is constant. Another consequence is, for example, that integrating
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

or differential forms on Pⁿ does not cause convergence issues.

On a projective complex manifold X, cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...

groups of coherent sheaves are finitely generated. (The above example is H⁰(Pⁿ(C), O), the zero-th cohomology of the sheaf of holomorphic functions O). In the parlance of algebraic geometry, projective space is proper. The above results hold in this context, too.

For complex projective space, every complex submanifold X ⊂ Pⁿ(C) (i.e., a manifold cut out by holomorphic equations) is necessarily an algebraic variety (i.e., given by polynomial equations). This is Chow's theorem, it allows the direct use of algebraic-geometric methods for these ad hoc analytically defined objects.

As outlined above, lines in P² or more generally hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

s in Pⁿ always do intersect. This extends to non-linear objects, as well: appropriately defining the degree of an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...

, which is roughly the degree of the polynomials needed to define the curve (see Hilbert polynomial
Hilbert polynomial
In commutative algebra, the Hilbert polynomial of a graded commutative algebra or graded module is a polynomial in one variable that measures the rate of growth of the dimensions of its homogeneous components...

), it is true (over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...

k) that any two projective curves C₁, C₂ ⊂ Pⁿ(k) of degree e and f intersect in exactly ef points, counting them with multiplicities (see Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...

). This is applied, for example, in defining a group structure on the points of an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...

, like y² = x³−x+1. The degree of an elliptic curve is 3. Consider the line x = 1, which intersects the curve (inside affine space) exactly twice, namely in (1, 1) and (1,
−1). However, inside P², the projective closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...

of the curve is given by the homogeneous equation

y²·z = x³−x·z²+z³,

which intersects the line (given inside P² by x = z) in three points: [1: 1: 1], [1: −1: 1] (corresponding to the two points mentioned above), and [0: 1: 0].

Any projective group variety, i.e. a projective variety, whose points form an abstract group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

, is necessarily an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...

, i.e. the group operation is commutative. Elliptic curves are examples for abelian varieties. The commutativity fails for non-projective group varieties, as the example GL_n(k) (the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...

) shows.

Axioms for projective space

A projective space S can be defined abstractly as a set P (the set of points), together with a set L of subsets of P (the set of lines), satisfying these axioms :

Each two distinct points p and q are in exactly one line.
Veblen
Oswald Veblen
Oswald Veblen was an American mathematician, geometer and topologist, whose work found application in atomic physics and the theory of relativity. He proved the Jordan curve theorem in 1905.-Life:...

's axiom: If a, b, c, d are distinct points and the lines through ab and cd meet, then so do the lines through ac and bd.
Any line has at least 3 points on it.

The last axiom eliminates reducible cases that can be written as a disjoint union of projective spaces together with 2-point lines joining any two points in distinct projective spaces. More abstractly, it can be defined as an incidence structure

Incidence structure

In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...

consisting of a set P of points, a set L of lines, and an incidence relation I stating which points lie on which lines.

A subspace of the projective space is a subset X, such that any line containing two points of X is a subset of X. The full space and the empty space are subspaces.

The geometric dimension of the space is said to be n if that is the largest number for which there is a strictly ascending chain of subspaces of this form:

Classification

Dimension 0 (no lines): The space is a single point.
Dimension 1 (exactly one line): All points lie on the unique line.
Dimension 2: There are at least 2 lines, and any two lines meet. A projective space for n = 2 is equivalent to a projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

. These are much harder to classify, as not all of them are isomorphic with a PG(d, K). The Desarguesian plane
Desarguesian plane
In projective geometry a Desarguesian plane, named after Gérard Desargues, is a plane in which Desargues' theorem holds. The ordinary real projective plane is a Desarguesian plane. More generally any projective plane over a division ring is Desarguesian, and conversely Hilbert showed that any...

s satisfying Desargues's theorem are projective planes over division rings, but there are many non-Desarguesian plane
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...

s.
Dimension at least 3: Two non-intersecting lines exist. proved the Veblen-Young theorem that every projective space of dimension n ≥ 3 is isomorphic with a PG(n, K), the n-dimensional projective space over some division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...

K.

There are

1, 1, 1, 1, 0, 1, 1, 4, 0, …

projective planes of order 2, 3, 4, …, 10. The numbers beyond this are very hard to calculate.

The smallest projective plane is the Fano plane

Fano plane

In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...

, PG[2,2] with 7 points and 7 lines.

Morphisms

Injective linear maps T ∈ L(V,W) between two vector spaces V and W over the same field k induce mappings of the corresponding projective spaces P(V) → P(W) via:

[v]→ [T(v)],

where v is a non-zero element of V and [...] denotes the equivalence classes of a vector under the defining identification of the respective projective spaces. Since members of the equivalence class differ by a scalar factor, and linear maps preserve scalar factors, this induced map is well-defined

Well-defined

In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...

. (If T is not injective, it will have a null space

Null space

In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...

larger than {0}; in this case the meaning of the class of T(v) is problematic if v is non-zero and in the null space. In this case one obtains a so-called rational map, see also birational geometry

Birational geometry

In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...

).

Two linear maps S and T in L(V,W) induce the same map between P(V) and P(W) if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

they differ by a scalar multiple of the identity, that is if T=λS for some λ ≠ 0. Thus if one identifies the scalar multiples of the identity map

Identity function

In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...

with the underlying field, the set of k-linear morphism

Morphism

In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...

s from P(V) to P(W) is simply P(L(V,W)).

The automorphism

Automorphism

In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...

s P(V) → P(V) can be described more concretely. (We deal only with automorphisms preserving the base field k). Using the notion of sheaves generated by global sections

Ample line bundle

, it can be shown that any algebraic (not necessarily linear) automorphism has to be linear, i.e. coming from a (linear) automorphism of the vector space V. The latter form the group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

GL(V)

General linear group

In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...

. By identifying maps which differ by a scalar, one concludes

Aut(P(V)) = Aut(V)/k^∗ = GL(V)/k^∗ =: PGL(V),

the quotient group

Quotient group

In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...

of GL(V) modulo the matrices which are scalar multiples of the identity. (These matrices form the center of Aut(V)). The groups PGL are called projective linear group

Projective linear group

In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...

s. The automorphisms of the complex projective line P¹(C) are called Möbius transformations.

Dual projective space

When the construction above is applied to the dual space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

V* rather than V, one obtains the dual projective space, which can be canonically identified with the space of hyperplanes through the origin of V. That is, if V is n dimensional, then P(V*) is the Grassmannian

Grassmannian

In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...

of n−1 planes in V.

In algebraic geometry, this construction allows for greater flexibility in the construction of projective bundles. One would like to be able associate a projective space to every quasi-coherent sheaf E over a scheme Y, not just the locally free ones. See EGA

Éléments de géométrie algébrique

The Éléments de géométrie algébrique by Alexander Grothendieck , or EGA for short, is a rigorous treatise, in French, on algebraic geometry that was published from 1960 through 1967 by the Institut des Hautes Études Scientifiques...

_II, Chap. II, par. 4 for more details.

Generalizations

dimension: The projective space, being the "space" of all one-dimensional linear subspaces of a given vector space V is generalized to Grassmannian manifold, which is parametrizing higher-dimensional subspaces (of some fixed dimension) of V.
sequence of subspaces: More generally flag manifold

Flag manifold

In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...

is the space of flags, i.e. chains of linear subspaces of V.
other subvarieties: Even more generally, moduli space

Moduli space

In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...

s parametrize objects such as elliptic curve

Elliptic curve

In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...

s of a given kind.
other rings: Generalizing to associative rings (rather than fields) yields inversive ring geometry

Inversive ring geometry

In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....

patching: Patching projective spaces together yields projective space bundles.

Severi–Brauer varieties are algebraic varieties over a field k which become isomorphic to projective spaces after an extension of the base field k.

Projective spaces are special cases of toric varieties. Another generalisation are weighted projective spaces.

Generalizations

Grassmannian manifold
Inversive ring geometry
Inversive ring geometry
In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....
Space (mathematics)

External links

http://planetmath.org/encyclopedia/ProjectiveSpace.html
Projective Planes of Small Order

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.