
Determinant
Encyclopedia
In linear algebra
, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well. The determinant provides important information when the matrix is that of the coefficients of a system of linear equations, or when it corresponds to a linear transformation
of a vector space: in the first case the system has a unique solution if and only if
the determinant is nonzero, in the second case that same condition means that the transformation has an inverse operation. A geometric interpretation can be given to the value of the determinant of a square matrix with real
entries: the absolute value
of the determinant gives the scale factor
by which area or volume is multiplied under the associated linear transformation, while its sign indicates whether the transformation preserves orientation. Thus a 2 × 2 matrix with determinant −2, when applied to a region of the plane with finite area, will transform that region into one with twice the area, while reversing its orientation.
Determinants occur throughout mathematics. The use of determinants in calculus
includes the Jacobian determinant in the substitution rule for integral
s of functions of several variables. They are used to define the characteristic polynomial
of a matrix that is an essential tool in eigenvalue problems in linear algebra. In some cases they are used just as a compact notation for expressions that would otherwise be unwieldy to write down.
The determinant of a matrix A is denoted det(A), det A, or |A|. In the case where the matrix entries are written out in full, the determinant is denoted by surrounding the matrix entries by vertical bars instead of the brackets or parentheses of the matrix. For instance, the determinant of the matrix is written
is written  and has the value
and has the value  .
.
Although most often used for matrices whose entries are real
or complex number
s, the definition of the determinant only involves addition, subtraction and multiplication, and so it can be defined for square matrices with entries taken from any commutative ring
. Thus for instance the determinant of a matrix with integer
coefficients will be an integer, and the matrix has an inverse with integer coefficients if and only if this determinant is 1 or −1 (these being the only invertible
elements of the integers). For square matrices with entries in a non-commutative ring, for instance the quaternion
s, there is no unique definition for the determinant, and no definition that has all the usual properties of determinants over commutative rings.

where the are vectors of size n, then the determinant of A is defined so that
are vectors of size n, then the determinant of A is defined so that


where b and c are scalars, v is any vector of size n and I is the identity matrix of size n. These properties state that the determinant is an alternating multilinear function of the columns, and they suffice to uniquely calculate the determinant of any square matrix. Provided the underlying scalars form a field (more generally, a commutative ring with unity), the definition below shows that such a function exists, and it can be shown to be unique.
Equivalently, the determinant can be expressed as a sum of products of entries of the matrix where each product has n terms and the coefficient of each product is -1 or 1 or 0 according to a given rule: it is a polynomial expression
of the matrix entries. This expression grows rapidly with the size of the matrix (an n-by-n matrix contributes n!
terms), so it will first be given explicitly for the case of 2-by-2 matrices and 3-by-3 matrices, followed by the rule for arbitrary size matrices, which subsumes these two cases.
Assume is a square matrix with rows and columns, so that it can be written as
The entries can be numbers or expressions (as happens when the determinant is used to define a characteristic polynomial
); the definition of the determinant depends only on the fact that they can be added and multiplied together in a commutative
manner.
The determinant of is denoted as , or it can be denoted directly in terms of the matrix entries by writing enclosing bars instead of brackets:
 The determinant of a 2×2 matrix is defined by
The determinant of a 2×2 matrix is defined by
If the matrix entries are real numbers, the matrix can be used to represent two linear mappings: one that maps the standard basis vectors to the rows of , and one that maps them to the columns of . In either case, the images of the basis vectors form a parallelogram that represents the image of the unit square under the mapping. The parallelogram defined by the rows of the above matrix is the one with vertices at (0,0), (a,b), (a + c, b + d), and (c,d), as shown in the accompanying diagram. The absolute value of is the area of the parallelogram, and thus represents the scale factor by which areas are transformed by . (The parallelogram formed by the columns of is in general a different parallelogram, but since the determinant is symmetric with respect to rows and columns, the area will be the same.)
is the area of the parallelogram, and thus represents the scale factor by which areas are transformed by . (The parallelogram formed by the columns of is in general a different parallelogram, but since the determinant is symmetric with respect to rows and columns, the area will be the same.)
The absolute value of the determinant together with the sign becomes the oriented area of the parallelogram. The oriented area is the same as the usual area, except that it is negative when the angle from the first to the second vector defining the parallelogram turns in a clockwise direction (which is opposite to the direction one would get for the identity matrix
).
Thus the determinant gives the scaling factor and the orientation induced by the mapping represented by . When the determinant is equal to one, the linear mapping defined by the matrix represents is equi-areal and orientation-preserving.
 The determinant of a 3×3 matrix
The determinant of a 3×3 matrix
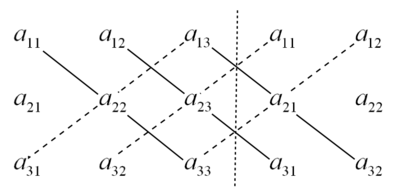 The rule of Sarrus
The rule of Sarrus
is a mnemonic for this formula: the sum of the products of three diagonal north-west to south-east lines of matrix elements, minus the sum of the products of three diagonal south-west to north-east lines of elements when the copies of the first two columns of the matrix are written beside it as in the illustration at the right.
For example, the determinant of
is calculated using this rule:
This scheme for calculating the determinant of a 3×3 matrix does not carry over into higher dimensions.
.
The Leibniz formula for the determinant of an n-by-n matrix A is

Here the sum is computed over all permutation
s σ of the set A permutation is a function that reorders this set of integers. The position of the element i after the reordering σ is denoted σi. For example, for n = 3, the original sequence 1, 2, 3 might be reordered to S = [2, 3, 1], with S1 = 2, S2 = 3, S3 = 1. The set of all such permutations (also known as the symmetric group
on n elements) is denoted Sn. For each permutation σ, sgn(σ) denotes the signature of σ; it is +1 for even
σ and −1 for odd σ. Evenness or oddness can be defined as follows: the permutation is even (odd) if the new sequence can be obtained by an even number (odd, respectively) of switches of numbers. For example, starting from [1, 2, 3] (and starting with the convention that the signature sgn([1,2,3]) = +1) and switching the positions of 2 and 3 yields [1, 3, 2], with sgn([1,3,2]) = –1. Switching once more yields [3, 1, 2], with sgn([3,1,2]) = +1 again. Finally, after a total of three switches (an odd number), the resulting permutation is [3, 2, 1], with sgn([3,2,1]) = –1. Therefore [3, 2, 1] is an odd permutation. Similarly, the permutation [2, 3, 1] is even: [1, 2, 3] → [2, 1, 3] → [2, 3, 1], with an even number of switches.
A permutation cannot be simultaneously even and odd, but sometimes it is convenient to accept non-permutations: sequences with repeated or skipped numbers, like [1, 2, 1]. In that case, the signature of any non-permutation is zero: sgn([1,2,1]) = 0.
In any of the summands, the term
summands, the term

is notation for the product of the entries at positions (i, σi), where i ranges from 1 to n:

For example, the determinant of a 3 by 3 matrix A (n = 3) is

This agrees with the rule of Sarrus given in the previous section.
The formal extension to arbitrary dimensions was made by Tullio Levi-Civita
, see (Levi-Civita symbol
) using a pseudo-tensor
symbol.
as follows:
These properties, which follow from the Leibniz formula, already completely characterize the determinant; in other words the determinant is the unique function from n×n matrices to scalars that is n-linear alternating in the columns, and takes the value 1 for the identity matrix (this characterization holds even if scalars are taken in any given commutative ring
). To see this it suffices to expand the determinant by multi-linearity in the columns into a (huge) linear combination of determinants of matrices in which each column is a standard basis
vector. These determinants are either 0 (by property 3) or else ±1 (by properties 1 and 7 below), so the linear combination gives the expression above in terms of the Levi-Civita symbol. While less technical in appearance, this characterization cannot entirely replace the Leibniz formula in defining the determinant, since without it the existence of an appropriate function is not clear. For matrices over non-commutative rings, properties 1 and 2 are incompatible for , so there is no good definition of the determinant in this setting.
These properties can be used to facilitate the computation of determinants by simplifying the matrix to the point where the determinant can be determined immediately. Specifically, for matrices with coefficients in a field
, properties 7 and 8 can be used to transform any matrix into a triangular matrix, whose determinant is given by property 9; this is essentially the method of Gaussian elimination
.
For example, the determinant of

can be computed using the following matrices:

Here, B is obtained from A by adding −1/2 × the first row to the second, so that det(A) = det(B). C is obtained from B by adding the first to the third row, so that det(C) = det(B). Finally, D is obtained from C by exchanging the second and third row, so that det(D) = −det(C). The determinant of the (upper) triangular matrix D is the product of its entries on the main diagonal: (−2) · 2 · 4.5 = −18. Therefore det(A) = +18.

Thus the determinant is a multiplicative map. This property is a consequence of the characterization given above of the determinant as the unique n-linear alternating function of the columns with value 1 on the identity matrix, since the function that maps can easily be seen to be n-linear and alternating in the columns of M, and takes the value at the identity. The formula can be generalized to (square) products of rectangular matrices, giving the Cauchy-Binet formula
, which also provides an independent proof of the multiplicative property.
The determinant det(A) of a matrix A is non-zero if and only if A is invertible or, yet another equivalent statement, if its rank
equals the size of the matrix. If so, the determinant of the inverse matrix is given by
In particular, products and inverses of matrices with determinant one still have this property. Thus, the set of such matrices (of fixed size n) form a group known as the special linear group
. More generally, the word "special" indicates the subgroup of another matrix group
of matrices of determinant one. Examples include the special orthogonal group (which if n is 2 or 3 consists of all rotation matrices), and the special unitary group
.
expresses the determinant of a matrix in terms of its minors. The minor Mi,j is defined to be the determinant of the (n−1)×(n−1)-matrix that results from A by removing the i-th row and the j-th column. The expression (−1)i+jMi,j is known as cofactor
. The determinant of A is given by

Calculating det(A) by means of that formula is referred to as expanding the determinant along a row or column. For the example 3-by-3 matrix , Laplace expansion along the second column (j = 2, the sum runs over i) yields:
, Laplace expansion along the second column (j = 2, the sum runs over i) yields:
However, Laplace expansion is efficient for small matrices only.
The adjugate matrix
adj(A) is the transpose of the matrix consisting of the cofactors, i.e.,
states that for A, an m-by-n matrix, and B, an n-by-m matrix,
 ,
,
where and
and  are the m-by-m and n-by-n identity matrices, respectively.
are the m-by-m and n-by-n identity matrices, respectively.
For the case of column vector c and row vector r, each with m components, the formula allows the quick calculation of the determinant of a matrix that differs from the identity matrix by a matrix of rank 1:
 .
.
More generally, for any invertible m-by-m matrix X,
 ,
,
and .
.

where I is the identity matrix
of the same dimension as A. Conversely, det(A) is the product of the eigenvalues of A, counted with their algebraic multiplicities. The product of all non-zero eigenvalues is referred to as pseudo-determinant
.
An Hermitian matrix is positive definite if all its eigenvalues are positive. Sylvester's criterion
asserts that this is equivalent to the determinants of the submatrices
being positive, for all k between 1 and n.
The trace
tr(A) is by definition the sum of the diagonal entries of A and also equals the sum of the eigenvalues. Thus, for complex matrices A,
or, for real matrices A,
Here exp(A) denotes the matrix exponential
of A, because every eigenvalue λ of A corresponds to the eigenvalue exp(λ) of exp(A). In particular, given any logarithm of A, that is, any matrix L satisfying
the determinant of A is given by
For example, for n = 2 and n = 3, respectively,

These formulae are closely related to Newton's identities.
A generalization of the above identities can be obtained from the following Taylor series expansion of the determinant:
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well. The determinant provides important information when the matrix is that of the coefficients of a system of linear equations, or when it corresponds to a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
of a vector space: in the first case the system has a unique solution if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the determinant is nonzero, in the second case that same condition means that the transformation has an inverse operation. A geometric interpretation can be given to the value of the determinant of a square matrix with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
entries: the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the determinant gives the scale factor
Scale factor
A scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
by which area or volume is multiplied under the associated linear transformation, while its sign indicates whether the transformation preserves orientation. Thus a 2 × 2 matrix with determinant −2, when applied to a region of the plane with finite area, will transform that region into one with twice the area, while reversing its orientation.
Determinants occur throughout mathematics. The use of determinants in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
includes the Jacobian determinant in the substitution rule for integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s of functions of several variables. They are used to define the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of a matrix that is an essential tool in eigenvalue problems in linear algebra. In some cases they are used just as a compact notation for expressions that would otherwise be unwieldy to write down.
The determinant of a matrix A is denoted det(A), det A, or |A|. In the case where the matrix entries are written out in full, the determinant is denoted by surrounding the matrix entries by vertical bars instead of the brackets or parentheses of the matrix. For instance, the determinant of the matrix
 is written
is written  and has the value
and has the value  .
.Although most often used for matrices whose entries are real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, the definition of the determinant only involves addition, subtraction and multiplication, and so it can be defined for square matrices with entries taken from any commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. Thus for instance the determinant of a matrix with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients will be an integer, and the matrix has an inverse with integer coefficients if and only if this determinant is 1 or −1 (these being the only invertible
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
elements of the integers). For square matrices with entries in a non-commutative ring, for instance the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, there is no unique definition for the determinant, and no definition that has all the usual properties of determinants over commutative rings.
Definition
There are various ways to define the determinant of a square matrix A, i.e. one with the same number of rows and columns. Perhaps the most natural way is expressed in terms of the columns of the matrix. If we write an n-by-n matrix in terms of its column vectors
where the
 are vectors of size n, then the determinant of A is defined so that
are vectors of size n, then the determinant of A is defined so that


where b and c are scalars, v is any vector of size n and I is the identity matrix of size n. These properties state that the determinant is an alternating multilinear function of the columns, and they suffice to uniquely calculate the determinant of any square matrix. Provided the underlying scalars form a field (more generally, a commutative ring with unity), the definition below shows that such a function exists, and it can be shown to be unique.
Equivalently, the determinant can be expressed as a sum of products of entries of the matrix where each product has n terms and the coefficient of each product is -1 or 1 or 0 according to a given rule: it is a polynomial expression
Polynomial expression
In mathematics, and in particular in the field of algebra, a polynomial expression in one or more given entities E1, E2, ..., is any meaningful expression constructed from copies of those entities together with constants, using the operations of addition and multiplication...
of the matrix entries. This expression grows rapidly with the size of the matrix (an n-by-n matrix contributes n!
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
terms), so it will first be given explicitly for the case of 2-by-2 matrices and 3-by-3 matrices, followed by the rule for arbitrary size matrices, which subsumes these two cases.
Assume is a square matrix with rows and columns, so that it can be written as

The entries can be numbers or expressions (as happens when the determinant is used to define a characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
); the definition of the determinant depends only on the fact that they can be added and multiplied together in a commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
manner.
The determinant of is denoted as , or it can be denoted directly in terms of the matrix entries by writing enclosing bars instead of brackets:

2-by-2 matrices


If the matrix entries are real numbers, the matrix can be used to represent two linear mappings: one that maps the standard basis vectors to the rows of , and one that maps them to the columns of . In either case, the images of the basis vectors form a parallelogram that represents the image of the unit square under the mapping. The parallelogram defined by the rows of the above matrix is the one with vertices at (0,0), (a,b), (a + c, b + d), and (c,d), as shown in the accompanying diagram. The absolute value of
 is the area of the parallelogram, and thus represents the scale factor by which areas are transformed by . (The parallelogram formed by the columns of is in general a different parallelogram, but since the determinant is symmetric with respect to rows and columns, the area will be the same.)
is the area of the parallelogram, and thus represents the scale factor by which areas are transformed by . (The parallelogram formed by the columns of is in general a different parallelogram, but since the determinant is symmetric with respect to rows and columns, the area will be the same.)The absolute value of the determinant together with the sign becomes the oriented area of the parallelogram. The oriented area is the same as the usual area, except that it is negative when the angle from the first to the second vector defining the parallelogram turns in a clockwise direction (which is opposite to the direction one would get for the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
).
Thus the determinant gives the scaling factor and the orientation induced by the mapping represented by . When the determinant is equal to one, the linear mapping defined by the matrix represents is equi-areal and orientation-preserving.
3-by-3 matrices



Rule of Sarrus
Sarrus' rule or Sarrus' scheme is a method and a memorization scheme to compute the determinant of a 3×3 matrix. It is named after the French mathematician Pierre Frédéric Sarrus....
is a mnemonic for this formula: the sum of the products of three diagonal north-west to south-east lines of matrix elements, minus the sum of the products of three diagonal south-west to north-east lines of elements when the copies of the first two columns of the matrix are written beside it as in the illustration at the right.
For example, the determinant of

is calculated using this rule:
 |
 |
 |
 |
||
 |
 |
This scheme for calculating the determinant of a 3×3 matrix does not carry over into higher dimensions.
n-by-n matrices
The determinant of a matrix of arbitrary size can be defined by the Leibniz formula or the Laplace formulaLaplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
.
The Leibniz formula for the determinant of an n-by-n matrix A is

Here the sum is computed over all permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s σ of the set A permutation is a function that reorders this set of integers. The position of the element i after the reordering σ is denoted σi. For example, for n = 3, the original sequence 1, 2, 3 might be reordered to S = [2, 3, 1], with S1 = 2, S2 = 3, S3 = 1. The set of all such permutations (also known as the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on n elements) is denoted Sn. For each permutation σ, sgn(σ) denotes the signature of σ; it is +1 for even
Even and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
σ and −1 for odd σ. Evenness or oddness can be defined as follows: the permutation is even (odd) if the new sequence can be obtained by an even number (odd, respectively) of switches of numbers. For example, starting from [1, 2, 3] (and starting with the convention that the signature sgn([1,2,3]) = +1) and switching the positions of 2 and 3 yields [1, 3, 2], with sgn([1,3,2]) = –1. Switching once more yields [3, 1, 2], with sgn([3,1,2]) = +1 again. Finally, after a total of three switches (an odd number), the resulting permutation is [3, 2, 1], with sgn([3,2,1]) = –1. Therefore [3, 2, 1] is an odd permutation. Similarly, the permutation [2, 3, 1] is even: [1, 2, 3] → [2, 1, 3] → [2, 3, 1], with an even number of switches.
A permutation cannot be simultaneously even and odd, but sometimes it is convenient to accept non-permutations: sequences with repeated or skipped numbers, like [1, 2, 1]. In that case, the signature of any non-permutation is zero: sgn([1,2,1]) = 0.
In any of the
 summands, the term
summands, the term
is notation for the product of the entries at positions (i, σi), where i ranges from 1 to n:

For example, the determinant of a 3 by 3 matrix A (n = 3) is

This agrees with the rule of Sarrus given in the previous section.
The formal extension to arbitrary dimensions was made by Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
, see (Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
) using a pseudo-tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
symbol.
Levi-Civita symbol
The determinant for an n-by-n matrix can be expressed in terms of the totally antisymmetric Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
as follows:
Properties of the determinant
The determinant has many properties. Some basic properties of determinants are:- The determinant of the n×n identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
equals 1. - Viewing an n×n matrix as being composed of n columns, the determinant is an n-linear function. This means that if one column of a matrix is written as a sum of two column vectors, and all other columns are left unchanged, then the determinant of is the sum determinants of the matrices obtained from by replacing the column by respectively by (and a similar relation holds when writing a column as a scalar multiple of a column vector).
- This n-linear function is an alternating form. This means that whenever two columns of a matrix are identical, its determinant is 0.
These properties, which follow from the Leibniz formula, already completely characterize the determinant; in other words the determinant is the unique function from n×n matrices to scalars that is n-linear alternating in the columns, and takes the value 1 for the identity matrix (this characterization holds even if scalars are taken in any given commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
). To see this it suffices to expand the determinant by multi-linearity in the columns into a (huge) linear combination of determinants of matrices in which each column is a standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
vector. These determinants are either 0 (by property 3) or else ±1 (by properties 1 and 7 below), so the linear combination gives the expression above in terms of the Levi-Civita symbol. While less technical in appearance, this characterization cannot entirely replace the Leibniz formula in defining the determinant, since without it the existence of an appropriate function is not clear. For matrices over non-commutative rings, properties 1 and 2 are incompatible for , so there is no good definition of the determinant in this setting.
- A matrix and its transpose have the same determinant. This implies that properties for columns have their counterparts in terms of rows:
- Viewing an n×n matrix as being composed of n rows, the determinant is an n-linear function.
- This n-linear function is an alternating form: whenever two rows of a matrix are identical, its determinant is 0.
- Interchanging two columns of a matrix multiplies its determinant by −1. This follows from properties 2 and 3 (it is a general property of multilinear alternating maps). Iterating gives that more generally a permutation of the columns multiplies the determinant by the sign of the permutation. Similarly a permutation of the rows multiplies the determinant by the sign of the permutation.
- Adding a scalar multiple of one column to another column does not change the value of the determinant. This is a consequence of properties 2 and 3: by property 2 the determinant changes by a multiple of the determinant of a matrix with two equal columns, which determinant is 0 by property 3. Similarly, adding a scalar multiple of one row to another row leaves the determinant unchanged.
- If A is a triangular matrixTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, i.e. ai,j = 0 whenever i > j or, alternatively, whenever i < j, then its determinant equals the product of the diagonal entries:
While this can be deduced from earlier properties, it follows most easily directly from the Leibniz formula (or from the Laplace expansion), in which the identity permutation is the only one that gives a non-zero contribution. -
These properties can be used to facilitate the computation of determinants by simplifying the matrix to the point where the determinant can be determined immediately. Specifically, for matrices with coefficients in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, properties 7 and 8 can be used to transform any matrix into a triangular matrix, whose determinant is given by property 9; this is essentially the method of Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
.
For example, the determinant of

can be computed using the following matrices:

Here, B is obtained from A by adding −1/2 × the first row to the second, so that det(A) = det(B). C is obtained from B by adding the first to the third row, so that det(C) = det(B). Finally, D is obtained from C by exchanging the second and third row, so that det(D) = −det(C). The determinant of the (upper) triangular matrix D is the product of its entries on the main diagonal: (−2) · 2 · 4.5 = −18. Therefore det(A) = +18.
Multiplicativity and matrix groups
The determinant of a matrix product of square matrices equals the product of their determinants:
Thus the determinant is a multiplicative map. This property is a consequence of the characterization given above of the determinant as the unique n-linear alternating function of the columns with value 1 on the identity matrix, since the function that maps can easily be seen to be n-linear and alternating in the columns of M, and takes the value at the identity. The formula can be generalized to (square) products of rectangular matrices, giving the Cauchy-Binet formula
Cauchy-Binet formula
In linear algebra, the Cauchy–Binet formula, named after Augustin-Louis Cauchy and Jacques Philippe Marie Binet, is an identity for the determinant of the product of two rectangular matrices of transpose shapes . It generalizes the statement that the determinant of a product of square matrices is...
, which also provides an independent proof of the multiplicative property.
The determinant det(A) of a matrix A is non-zero if and only if A is invertible or, yet another equivalent statement, if its rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
equals the size of the matrix. If so, the determinant of the inverse matrix is given by

In particular, products and inverses of matrices with determinant one still have this property. Thus, the set of such matrices (of fixed size n) form a group known as the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
. More generally, the word "special" indicates the subgroup of another matrix group
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
of matrices of determinant one. Examples include the special orthogonal group (which if n is 2 or 3 consists of all rotation matrices), and the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
.
Laplace's formula and the adjugate matrix
Laplace's formulaLaplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
expresses the determinant of a matrix in terms of its minors. The minor Mi,j is defined to be the determinant of the (n−1)×(n−1)-matrix that results from A by removing the i-th row and the j-th column. The expression (−1)i+jMi,j is known as cofactor
Cofactor (linear algebra)
In linear algebra, the cofactor describes a particular construction that is useful for calculating both the determinant and inverse of square matrices...
. The determinant of A is given by

Calculating det(A) by means of that formula is referred to as expanding the determinant along a row or column. For the example 3-by-3 matrix
 , Laplace expansion along the second column (j = 2, the sum runs over i) yields:
, Laplace expansion along the second column (j = 2, the sum runs over i) yields:
 |
 |
 |
 |
 |
|
 |
 |
|
However, Laplace expansion is efficient for small matrices only.
The adjugate matrix
Adjugate matrix
In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....
adj(A) is the transpose of the matrix consisting of the cofactors, i.e.,

Sylvester's determinant theorem
Sylvester's determinant theoremSylvester's determinant theorem
In matrix theory, Sylvester's determinant theorem is a theorem useful for evaluating certain types of determinants. It is named after James Joseph Sylvester....
states that for A, an m-by-n matrix, and B, an n-by-m matrix,
 ,
,where
 and
and  are the m-by-m and n-by-n identity matrices, respectively.
are the m-by-m and n-by-n identity matrices, respectively.For the case of column vector c and row vector r, each with m components, the formula allows the quick calculation of the determinant of a matrix that differs from the identity matrix by a matrix of rank 1:
 .
.More generally, for any invertible m-by-m matrix X,
 ,
,and
 .
.Relation to eigenvalues and trace
Determinants can be used to find the eigenvalues of the matrix A: they are the solutions of the characteristic equationCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

where I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
of the same dimension as A. Conversely, det(A) is the product of the eigenvalues of A, counted with their algebraic multiplicities. The product of all non-zero eigenvalues is referred to as pseudo-determinant
Pseudo-determinant
In linear algebra and statistics, the pseudo-determinant is the product of all non-zero eigenvalues of a square matrix. It coincides with the regular determinant when the matrix is non-singular.- Definition :...
.
An Hermitian matrix is positive definite if all its eigenvalues are positive. Sylvester's criterion
Sylvester's criterion
In mathematics, Sylvester’s criterion is a necessary and sufficient criterion to determine whether a Hermitian matrix is positive-definite. It is named after James Joseph Sylvester....
asserts that this is equivalent to the determinants of the submatrices

being positive, for all k between 1 and n.
The trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
tr(A) is by definition the sum of the diagonal entries of A and also equals the sum of the eigenvalues. Thus, for complex matrices A,

or, for real matrices A,

Here exp(A) denotes the matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
of A, because every eigenvalue λ of A corresponds to the eigenvalue exp(λ) of exp(A). In particular, given any logarithm of A, that is, any matrix L satisfying

the determinant of A is given by

For example, for n = 2 and n = 3, respectively,


These formulae are closely related to Newton's identities.
A generalization of the above identities can be obtained from the following Taylor series expansion of the determinant:
-

where I is the identity matrix.
Cramer's rule
For a matrix equation
the solution is given by Cramer's ruleCramer's ruleIn linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
:
where Ai is the matrix formed by replacing the i-th column of A by the column vector b. This follows immediately by column expansion of the determinant, i.e.
where the vectors are the columns of A. The rule is also implied by the identity
are the columns of A. The rule is also implied by the identity

It has recently been shown that Cramer's rule can be implemented in O(n3) time, which is comparable to more common methods of solving systems of linear equations, such as LULU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
, QRQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
, or singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
.
Block matrices
Suppose A, B, C, and D are n×n-, n×m-, m×n-, and m×m-matrices, respectively. Then

This can be seen from the Leibniz formula or by induction on n. When A is invertible, employing the following identity

leads to

When D is invertible, a similar identity with factored out can be derived analogously, that is,
factored out can be derived analogously, that is,

When the blocks are square matrices of the same order further formulas hold. For example, if C and D commute (i.e., CD = DC), then the following formula comparable to the determinant of a 2-by-2 matrix holds:
Derivative
By definition, e.g., using the Leibniz formula, the determinant of real (or analogously for complex) square matrices is a polynomial functionPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
from Rn×n to R. As such it is everywhere differentiableDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. Its derivative can be expressed using Jacobi's formulaJacobi's formulaIn matrix calculus, Jacobi's formula expresses the derivative of the determinant of a matrix A in terms of the adjugate of A and the derivative of A...
:

where adj(A) denotes the adjugate of A. In particular, if A is invertible, we have

Expressed in terms of the entries of A, these are
Yet another equivalent formulation is
 ,
,
using big O notationBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
. The special case where , the identity matrix, yields
, the identity matrix, yields

This identity is used in describing the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of certain matrix Lie groups.
If the matrix A is written as where a, b, c are vectors, then the gradient over one of the three vectors may be written as the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
where a, b, c are vectors, then the gradient over one of the three vectors may be written as the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of the other two:
-

Determinant of an endomorphism
The above identities concerning the determinant of a products and inverses of matrices imply that similar matrices have the same determinant: two matrices A and B are similar, if there exists an invertible matrix X such that A = X−1BX. Indeed, repeatedly applying the above identities yields

The determinant is therefore also called a similarity invariant. The determinant of a linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
for some finite dimensional vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is defined to be the determinant of the matrix describing it, with respect to an arbitrary choice of basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
in V. By the similarity invariance, this determinant is independent of the choice of the basis for V and therefore only depends on the endomorphism T.
Exterior algebra
The determinant can also be characterized as the unique function
from the set of all n-by-n matrices with entries in a field K to this field satisfying the following three properties: first, D is an n-linear function: considering all but one column of A fixed, the determinant is linear in the remaining column, that is
for any column vectors v1, ..., vn, and w and any scalars (elements of K) a and b. Second, D is an alternating function: for any matrix A with two identical columns . Finally, D(In) = 1. Here In is the identity matrix.
This fact also implies that any every other n-linear alternating function satisfies
The last part in fact follows from the preceding statement: one easily sees that if F is nonzero it satisfies , and function that associates to satisfies all conditions of the theorem. The importance of stating this part is mainly that it remains valid if K is any commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
rather than a field, in which case the given argument does not apply.
The determinant of a linear transformation A : V → V of an n-dimensional vector space V can be formulated in a coordinate-free manner by considering the n-th exterior powerExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
ΛnV of V. A induces a linear map

As ΛnV is one-dimensional, the map ΛnA is given by multiplying with some scalar. This scalar coincides with the determinant of A, that is to say
This definition agrees with the more concrete coordinate-dependent definition. This follows from the characterization of the determinant given above. For example, switching two columns changes the parity of the determinant; likewise, permuting the vectors in the exterior product v1 ∧ v2 ∧ ... ∧ vn to v2 ∧ v1 ∧ v3 ∧ ... ∧ vn, say, also alters the parity.
For this reason, the highest non-zero exterior power Λn(V) is sometimes also called the determinant of V and similarly for more involved objects such as vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s or chain complexChain complexIn mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es of vector spaces. Minors of a matrix can also be cast in this setting, by considering lower alternating forms ΛkV with k < n.
Square matrices over commutative rings and abstract properties
The determinant of a matrix can be defined, for example using the Leibniz formula, for matrices with entries in any commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. Briefly, a ring is a structure where addition, subtraction, and multiplication are defined. The commutativity requirement means that the product does not depend on the order of the two factors, i.e.,
is supposed to hold for all elements r and s of the ring. For example, the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s form a commutative ring.
Many of the above statements and notions carry over mutatis mutandis to determinants of these more general matrices: the determinant is multiplicative in this more general situation, and Cramer's rule also holds. A square matrix over a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R is invertible if and only if its determinant is a unitUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in R, that is, an element having a (multiplicative) inverseInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
. (If R is a field, this latter condition is equivalent to the determinant being nonzero, thus giving back the above characterization.) For example, a matrix A with entries in Z, the integers, is invertible (in the sense that the inverse matrix has again integer entries) if the determinant is +1 or −1. Such a matrix is called unimodularUnimodular matrixIn mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...
.
The determinant defines a mapping between
the group of invertible n×n matrices with entries in R and the multiplicative groupMultiplicative groupIn mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of units in . Since it respects the multiplication in both groups, this map is a group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
. Secondly, given a ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
, there is a map given by replacing all entries in by their images under . The determinant respects these maps, i.e., given a matrix with entries in , the identity
holds. For example, the determinant of the complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of a complex matrix (which is also the determinant of its conjugate transpose) is the complex conjugate of its determinant, and for integer matrices: the reduction modulo of the determinant of such a matrix is equal to the determinant of the matrix reduced modulo (the latter determinant being computed using modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
). In the more high-brow parlance of category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the determinant is a natural transformationNatural transformationIn category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
between the two functors and . Adding yet another layer of abstraction, this is captured by saying that the determinant is a morphism of algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s, from the general linear group to the multiplicative groupMultiplicative groupIn mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
,
Infinite matrices
For matrices with an infinite number of rows and columns, the above definitions of the determinant do not carry over directly. For example, in Leibniz' formula, an infinite sum (all of whose terms are infinite products) would have to be calculated. Functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
provides different extensions of the determinant for such infinite-dimensional situations, which however only work for particular kinds of operators.
The Fredholm determinantFredholm determinantIn mathematics, the Fredholm determinant is a complex-valued function which generalizes the determinant of a matrix. It is defined for bounded operators on a Hilbert space which differ from the identity operator by a trace-class operator...
defines the determinant for operators known as trace class operators by an appropriate generalization of the formula
Another infinite-dimensional notion of determinant is the functional determinantFunctional determinantIn mathematics, if S is a linear operator mapping a function space V to itself, it is sometimes possible to define an infinite-dimensional generalization of the determinant. The corresponding quantity det is called the functional determinant of S.There are several formulas for the functional...
.
Notions of determinant over non-commutative rings
For square matrices with entries in a non-commutative ring, there are various difficulties in defining determinants in a manner analogous to that for commutative rings. A meaning can be given to the Leibniz formula provided the order for the product is specified, and similarly for other ways to define the determinant, but non-commutativity then leads to the loss of many fundamental properties of the determinant, for instance the multiplicative property or the fact that the determinant is unchanged under transposition of the matrix. Over non-commutative rings, there is no reasonable notion of a multilinear form (if a bilinear form exists with a regular elementRegular elementRegular element may refer to:* In ring theory, a nonzero element of a ring that is neither a left nor a right zero divisor* A regular element of a Lie algebra or Lie group....
of R as value on some pair of arguments, it can be used to show that all elements of R commute). Nevertheless various notions of non-commutative determinant have been formulated, which preserve some of the properties of determinants, notably quasideterminants and the Dieudonné determinantDieudonné determinantIn linear algebra, the Dieudonné determinant is a generalization of the determinant of a matrix to matrices over division rings.It was introduced by ....
.
Further variants
Determinants of matrices in superrings (that is, Z/2-graded rings) are known as BerezinianBerezinianIn mathematics and theoretical physics, the Berezinian or superdeterminant is a generalization of the determinant to the case of supermatrices. The name is for Felix Berezin...
s or superdeterminants.
The permanentPermanentThe permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
of a matrix is defined as the determinant, except that the factors sgn(σ) occurring in Leibniz' rule are omitted. The immanant generalizes both by introducing a character of the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn in Leibniz' rule.
Calculation
Determinants are mainly used as a theoretical tool. They are rarely calculated explicitly in numerical linear algebraNumerical linear algebraNumerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, where for applications like checking invertibility and finding eigenvalues the determinant has largely been supplanted by other techniques. Nonetheless, explicitly calculating determinants is required in some situations, and different methods are available to do so.
Naive methods of implementing an algorithm to compute the determinant include using Leibniz' formula or Laplace's formula. Both these approaches are extremely inefficient for large matrices, though, since the number of required operations grows very quickly: it is of orderBig O notationIn mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
n! (n factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
) for an n×n matrix M. For example, Leibniz' formula requires to calculate n! products. Therefore, more involved techniques have been developed for calculating determinants.
Decomposition methods
Given a matrix A, some methods compute its determinant by writing A as a product of matrices whose determinants can be more easily computed. Such techniques are referred to as decomposition methodDecomposition methodIn constraint satisfaction, a decomposition method translates a constraint satisfaction problem into another constraint satisfaction problem that is binary and acyclic. Decomposition methods work by grouping variables into sets, and solving a subproblem for each set...
s. Examples include the LU decompositionLU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
, Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
or the QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
. These methods are of order O(n3), which is a significant improvement over O(n!)
The LU decomposition expresses A in terms of a lower triangular matrix L, an upper triangular matrix U and a permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
P:
The determinants of L and U can be quickly calculated, since they are the products of the respective diagonal entries. The determinant of P is just the sign of the corresponding permutation. The determinant of A is then
of the corresponding permutation. The determinant of A is then

Moreover, the decomposition can be chosen such that L is a unitriangular matrix and therefore has determinant 1, in which case the formula further simplifies to

Further methods
If the determinant of A and the inverse of A have already been computed, the matrix determinant lemmaMatrix determinant lemmaIn mathematics, in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertiblematrix Aand the dyadic product, u vT,of a column vector u and a row vector vT.- Statement :...
allows to quickly calculate the determinant of , where u and v are column vectors.
Since the definition of the determinant does not need divisions, a question arises: do fast algorithms exist that do not need divisions? This is especially interesting for matrices over rings. Indeed algorithms with run-time proportional to n4 exist. An algorithm of Mahajan and Vinay, and Berkowitz is based on closed ordered walks (short clow). It computes more products than the determinant definition requires, but some of these products cancel and the sum of these products can be computed more efficiently. The final algorithm looks very much like an iterated product of triangular matrices.
If two matrices of order n can be multiplied in time M(n), where M(n)≥na for some a>2, then the determinant can be computed in time O(M(n)). This means, for example, that an O(n2.376) algorithm exists based on the Coppersmith–Winograd algorithmCoppersmith–Winograd algorithmIn the mathematical discipline of linear algebra, the Coppersmith–Winograd algorithm, named after Don Coppersmith and Shmuel Winograd, is the asymptotically fastest known algorithm for square matrix multiplication. It can multiply two n \times n matrices in O time...
.
Algorithms can also be assessed according to their bit complexity, i.e., how many bits of accuracy are needed to store intermediate values occurring in the computation. For example, the Gaussian eliminationGaussian eliminationIn linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
(or LU decomposition) methods is of order O(n3), but the bit length of intermediate values can become exponentially long. The Bareiss AlgorithmBareiss algorithmIn mathematics, the Bareiss algorithm, named after Erwin Bareiss, is an algorithm to calculate the determinant of a matrix with integer entries using only integer arithmetic; any divisions that are performed are guaranteed to be exact...
, on the other hand, is an exact-division method based on Sylvester's identitySylvester's determinant theoremIn matrix theory, Sylvester's determinant theorem is a theorem useful for evaluating certain types of determinants. It is named after James Joseph Sylvester....
is also of order n3, but the bit complexity is roughly the bit size of the original entries in the matrix times n.
History
Historically, determinants were considered without reference to matrices: originally, a determinant was defined as a property of a system of linear equations. The determinant "determines" whether the system has a unique solution (which occurs precisely if the determinant is non-zero). In this sense, determinants were first used in the Chinese mathematics textbook The Nine Chapters on the Mathematical ArtThe Nine Chapters on the Mathematical ArtThe Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
(九章算術, Chinese scholars, around the 3rd century BC). In Europe, two-by-two determinants were considered by CardanoGerolamo CardanoGerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
at the end of the 16th century and larger ones by LeibnizGottfried LeibnizGottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
.
In Europe, CramerGabriel CramerGabriel Cramer was a Swiss mathematician, born in Geneva. He showed promise in mathematics from an early age. At 18 he received his doctorate and at 20 he was co-chair of mathematics.In 1728 he proposed a solution to the St...
(1750) added to the theory, treating the subject in relation to sets of equations. The recurrence law was first announced by Bézout (1764).
It was Vandermonde (1771) who first recognized determinants as independent functions. Laplace (1772) gave the general method of expanding a determinant in terms of its complementary minors: Vandermonde had already given a special case. Immediately following, LagrangeJoseph Louis LagrangeJoseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
(1773) treated determinants of the second and third order. Lagrange was the first to apply determinants to questions of elimination theoryElimination theoryIn commutative algebra and algebraic geometry, elimination theory is the classical name for algorithmic approaches to eliminating between polynomials of several variables....
; he proved many special cases of general identities.
GaussCarl Friedrich GaussJohann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
(1801) made the next advance. Like Lagrange, he made much use of determinants in the theory of numbers. He introduced the word determinants (Laplace had used resultant), though not in the present signification, but rather as applied to the discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of a quantic. Gauss also arrived at the notion of reciprocal (inverse) determinants, and came very near the multiplication theorem.
The next contributor of importance is BinetJacques Philippe Marie BinetJacques Philippe Marie Binet was a French mathematician, physicist and astronomer born in Rennes; he died in Paris, France, in 1856. He made significant contributions to number theory, and the mathematical foundations of matrix algebra which would later lead to important contributions by Cayley...
(1811, 1812), who formally stated the theorem relating to the product of two matrices of m columns and n rows, which for the special case of m = n reduces to the multiplication theorem. On the same day (November 30, 1812) that Binet presented his paper to the Academy, Cauchy also presented one on the subject. (See Cauchy-Binet formulaCauchy-Binet formulaIn linear algebra, the Cauchy–Binet formula, named after Augustin-Louis Cauchy and Jacques Philippe Marie Binet, is an identity for the determinant of the product of two rectangular matrices of transpose shapes . It generalizes the statement that the determinant of a product of square matrices is...
.) In this he used the word determinant in its present sense, summarized and simplified what was then known on the subject, improved the notation, and gave the multiplication theorem with a proof more satisfactory than Binet's. With him begins the theory in its generality.
The next important figure was JacobiCarl Gustav Jakob JacobiCarl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
(from 1827). He early used the functional determinant which Sylvester later called the Jacobian, and in his memoirs in Crelle for 1841 he specially treats this subject, as well as the class of alternating functions which Sylvester has called alternants. About the time of Jacobi's last memoirs, SylvesterJames Joseph SylvesterJames Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
(1839) and CayleyArthur CayleyArthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
began their work.
The study of special forms of determinants has been the natural result of the completion of the general theory. Axisymmetric determinants have been studied by Lebesgue, HesseOtto HesseLudwig Otto Hesse was a German mathematician. Hesse was born in Königsberg, Prussia, and died in Munich, Bavaria. He worked on algebraic invariants...
, and Sylvester; persymmetric determinants by Sylvester and HankelHermann HankelHermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
; circulants by CatalanEugène Charles CatalanEugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville...
, SpottiswoodeWilliam SpottiswoodeWilliam Spottiswoode FRS was an English mathematician and physicist. He was President of the Royal Society from 1878 to 1883.-Early life:...
, GlaisherJames Whitbread Lee GlaisherJames Whitbread Lee Glaisher son of James Glaisher, the meteorologist, was a prolific English mathematician.He was educated at St Paul's School and Trinity College, Cambridge, where he was second wrangler in 1871...
, and Scott; skew determinants and PfaffianPfaffianIn mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
s, in connection with the theory of orthogonal transformation, by Cayley; continuants by Sylvester; WronskianWronskianIn mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
s (so called by MuirThomas Muir (mathematician)Sir Thomas Muir FRS was a Scottish mathematician, remembered as an authority on determinants. He was born in Stonebyres in South Lanarkshire, and brought up in the small town of Biggar. At the University of Glasgow he changed his studies from classics to mathematics after advice from the future...
) by ChristoffelElwin Bruno ChristoffelElwin Bruno Christoffel was a German mathematician and physicist.-Life:...
and FrobeniusFerdinand Georg FrobeniusFerdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
; compound determinants by Sylvester, Reiss, and Picquet; Jacobians and HessiansHessian matrixIn mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
by Sylvester; and symmetric gauche determinants by Trudi. Of the text-books on the subject Spottiswoode's was the first. In America, Hanus (1886), Weld (1893), and Muir/Metzler (1933) published treatises.
Linear independence
As mentioned above, the determinant of a matrix (with real or complex entries, say) is zero if and only if the column vectors of the matrix are linearly dependent. Thus, determinants can be used to characterize linearly dependent vectors. For example, given two vectors v1, v2 in R3, a third vector v3 lies in the planePlane-Physical objects:* Aeroplane or airplane, a fixed-wing aircraft* Plane , a woodworking tool to smooth surfaces* Platanus, a genus of trees with the common name "plane"* Acer pseudoplatanus, a tree species sometimes called "plane"...
spanned by the former two vectors exactly if the determinant of the 3-by-3 matrix consisting of the three vectors is zero. The same idea is also used in the theory of differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s: given n functions f1(x), ..., fn(x) (supposed to be n−1 times differentiable), the WronskianWronskianIn mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
is defined to be
It is non-zero (for some x) in a specified interval if and only if the given functions and all their derivatives up to order n−1 are linearly independent. If it can be shown that the Wronskian is zero everywhere on an interval then, in the case of analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s, this implies the given functions are linearly dependent. See the Wronskian and linear independence.
Orientation of a basis
The determinant can be thought of as assigning a number to every sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of n in Rn, by using the square matrix whose columns are the given vectors. For instance, an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
with entries in Rn represents an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
in Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The determinant of such a matrix determines whether the orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of the basis is consistent with or opposite to the orientation of the standard basisStandard basisIn mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
. Namely, if the determinant is +1, the basis has the same orientation. If it is −1, the basis has the opposite orientation.
More generally, if the determinant of A is positive, A represents an orientation-preserving linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
(if A is an orthogonal 2×2 or 3×3 matrix, this is a rotationRotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
), while if it is negative, A switches the orientation of the basis.
Volume and Jacobian determinant
As pointed out above, the absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the determinant of real vectors is equal to the volume of the parallelepipedParallelepipedIn geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
spanned by those vectors. As a consequence, if is the linear map represented by the matrix A, and S is any measurableLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Rn, then the volume of f(S) is given by |det(A)| times the volume of S. More generally, if the linear map is represented by the m-by-n matrix A, then the m-dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al volume of f(S) is given by:
By calculating the volume of the tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
bounded by four points, they can be used to identify skew lines. The volume of any tetrahedron, given its vertices a, b, c, and d, is (1/6)·|det(a − b, b − c, c − d)|, or any other combination of pairs of vertices that would form a spanning treeSpanning treeSpanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...
over the vertices.
For a general differentiable functionDifferentiable functionIn calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
, much of the above carries over by considering the Jacobian matrix of f. For
the Jacobian is the n-by-n matrix whose entries are given by
Its determinant, the Jacobian determinant appears in the higher-dimensional version of integration by substitutionIntegration by substitutionIn calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
: for suitable functions f and an open subset U of R'n (the domain of f), the integral over f(U) of some other function is given by
The Jacobian also occurs in the inverse function theoremInverse function theoremIn mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
.
Vandermonde determinant (alternant)
Third order
In general, the nth-order Vandermonde determinant is
where the right-hand side is the continued product of all the differences that can be formed from the n(n-1)/2 pairs of numbers taken from x1, x2, ... ,xn, with the order of the differences taken in the reversed order of the suffixes that are involved.
Circulants
Second order
Third order
where ω and ω2 are the complex cube roots of 1. In general, the nth-order circulant determinant is
where ωj is an nth root of 1.
See also
- Dieudonné determinantDieudonné determinantIn linear algebra, the Dieudonné determinant is a generalization of the determinant of a matrix to matrices over division rings.It was introduced by ....
- Matrix determinant lemmaMatrix determinant lemmaIn mathematics, in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertiblematrix Aand the dyadic product, u vT,of a column vector u and a row vector vT.- Statement :...
- PermanentPermanentThe permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
- Immanant
- PfaffianPfaffianIn mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
- Slater determinantSlater determinantIn quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
- Functional determinantFunctional determinantIn mathematics, if S is a linear operator mapping a function space V to itself, it is sometimes possible to define an infinite-dimensional generalization of the determinant. The corresponding quantity det is called the functional determinant of S.There are several formulas for the functional...
External links
- WebApp to calculate determinants and descriptively solve systems of linear equations
- Determinant Interactive Program and Tutorial
- Online Matrix Calculator
- Linear algebra: determinants. Compute determinants of matrices up to order 6 using Laplace expansion you choose.
- Matrices and Linear Algebra on the Earliest Uses Pages
- Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course.
- Instructional Video on taking the determinant of an nxn matrix (Khan Academy)
- Online matrix calculator (determinant, track, inverse, adjoint, transpose) Compute determinant of matrix up to order 8
- Dieudonné determinant
-




