
Quasideterminant
Encyclopedia
In mathematics, the quasideterminant is a replacement for the determinant
for matrices
with noncommutative entries. Example 2 × 2 quasideterminants are as follows:
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
for matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with noncommutative entries. Example 2 × 2 quasideterminants are as follows:
-
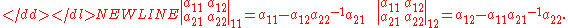
In general, there are n2 quasideterminants defined for an n × n matrix (one for each position in the matrix), but the presence of the inverted terms above should give the reader pause: they are not always defined, and even when they are defined, they do not reduce to determinants when the entries commute. Rather,
-

where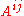 means delete the ith row and jth column from A.
means delete the ith row and jth column from A.
The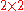 examples above were introduced between 1926 and 1928 by RichardsonArchibald Read RichardsonArchibald Read Richardson was a British mathematician known for his work in algebra.He collaborated with Dudley E. Littlewood on invariants and group representation theory...
examples above were introduced between 1926 and 1928 by RichardsonArchibald Read RichardsonArchibald Read Richardson was a British mathematician known for his work in algebra.He collaborated with Dudley E. Littlewood on invariants and group representation theory...
and Heyting,
but they were marginalized at the time because they were not polynomials in the entries of . These examples were rediscovered and given new life in 1991 by I.M. GelfandIsrael GelfandIsrael Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
. These examples were rediscovered and given new life in 1991 by I.M. GelfandIsrael GelfandIsrael Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and V.S. Retakh.
There, they develop quasideterminantal versions of many familiar determinantal properties. For example, if is built from
is built from  by rescaling its
by rescaling its 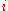 -th row (on the left) by
-th row (on the left) by 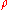 , then
, then 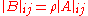 .
.
Similarly, if is built from
is built from  by adding a (left) multiple of the
by adding a (left) multiple of the 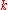 -th row to another row, then
-th row to another row, then 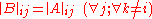 . They even develop a quasideterminantal
. They even develop a quasideterminantal
version of Cramer's ruleCramer's ruleIn linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
.
Definition
Let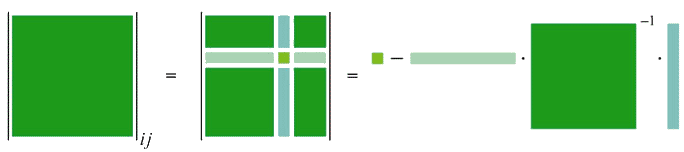
 be an
be an 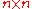 matrix over a (not necessarily commutative)
matrix over a (not necessarily commutative)
ring and fix
and fix 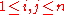 . Let
. Let 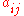
denote the ( )-entry of
)-entry of  , let
, let 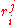 denote the
denote the 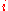 -th row of
-th row of  with column
with column 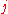 deleted, and let
deleted, and let 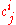 denote the
denote the 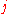 -th column of
-th column of  with row
with row 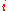 deleted. The (
deleted. The ( )-quasideterminant of
)-quasideterminant of  is defined if the submatrix
is defined if the submatrix 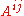 is invertible over
is invertible over  . In this case,
. In this case,
-

Recall the formula (for commutative rings) relating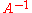 to the determinant, namely
to the determinant, namely 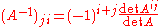 . The above definition is a generalization in that (even for noncommutative rings) one has
. The above definition is a generalization in that (even for noncommutative rings) one has
-
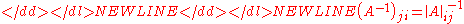
whenever the two sides makes sense.
Identities
One of the most important properties of the quasideterminant is what Gelfand and Retakh
call the “heredity principle.” It allows one to take a quasideterminant in
stages (and has no commutative counterpart). To illustrate, suppose-
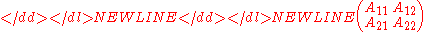
is a block matrixBlock matrixIn the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
decomposition of an matrix
matrix  with
with
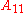 a
a 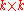 matrix. If the (
matrix. If the ( )-entry of
)-entry of  lies within
lies within 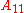 , it says that
, it says that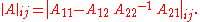
That is, the quasideterminant of a quasideterminant is a quasideterminant! To put it less succinctly: UNLIKE determinants, quasideterminants treat matrices with block-matrix entries no differently than ordinary matrices (something determinants cannot do since block-matrices generally don't commute with one another). That is, while the precise form of the above identity is quite surprising, the existence of some such identity is less so.
Other identities from the papers are (i) the so-called “homological relations,” stating that two quasideterminants in a common row or column are closely related to one another, and (ii) the SylvesterJames Joseph SylvesterJames Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
formula.
(i) Two quasideterminants sharing a common row or column satisfy-
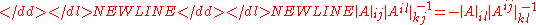
or-
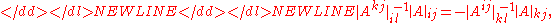
respectively, for all choices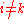 ,
,  so that the
so that the
quasideterminants involved are defined.
(ii) Like the heredity principle, the Sylvester identity is a way to recursively
compute a quasideterminant. To ease notation, we display a special case. Let
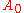 be the upper-left
be the upper-left 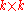 submatrix of an
submatrix of an
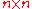 matrix
matrix  and fix a coordinate (
and fix a coordinate ( ) in
) in
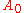 . Let
. Let 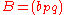 be the
be the 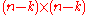 matrix, with
matrix, with 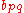 defined as the (
defined as the (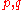 )-quasideterminant of the
)-quasideterminant of the 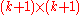 matrix formed by adjoining to
matrix formed by adjoining to 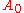 the first
the first 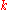 columns of row
columns of row 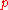 , the first
, the first 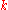 rows of column
rows of column 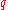 , and the entry
, and the entry 
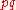 . Then one has
. Then one has
-
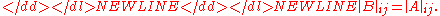
Many more identities have appeared since the first articles of Gelfand and Retakh on the subject, most of them being analogs of classical determinantal identities. An important source is Krob and Leclerc's 1995 article,
To highlight one, we consider the row/column expansion identities. Fix a row to expand along. Recall the determinantal formula
to expand along. Recall the determinantal formula
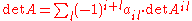 .
.
Well, it happens that quasideterminants satisfy-

(expansion along column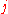 ), and
), and
-
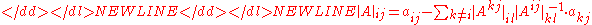
(expansion along row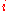 ).
).
Connections to other determinants
The quasideterminant is certainly not the only existing determinant analog for noncommutative settings—perhaps the most famous examples are the Dieudonné determinantDieudonné determinantIn linear algebra, the Dieudonné determinant is a generalization of the determinant of a matrix to matrices over division rings.It was introduced by ....
and quantumQuantum groupIn mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
determinant. However, these are related to the quasideterminant in some way. For example,-

with the factors on the right-hand side commuting with each other. Other famous examples, such as BerezinianBerezinianIn mathematics and theoretical physics, the Berezinian or superdeterminant is a generalization of the determinant to the case of supermatrices. The name is for Felix Berezin...
s, Moore and Study determinants, Capelli determinants, and Cartier-Foata-type determinants are also expressible in terms of quasideterminants. Gelfand has been known to define a (noncommutative) determinant as “good” if it may be expressed as products of quasiminors.
Applications
Paraphrasing their 2005 survey article with S. Gelfand and R. Wilson
,
Gelfand and Retakh advocate for the adoption of
quasideterminants as “a main organizing tool in noncommutative algebra, giving
them the same role determinants play in commutative algebra.” By now,
substantive use has been made of the quasideterminant in such fields of mathematics as
integrable systems,
representation theory,
algebraic combinatorics,
the theory of noncommutative symmetric functions,
the theory of polynomials over division rings,
and noncommutative geometry.
Several of the applications above make use of quasi-Plücker coordinates, which parametrize noncommutative Grassmannians and flags in much the same way as Plücker coordinatesPlücker embeddingIn mathematics, the Plücker embedding describes a method to realize the Grassmannian of all r-dimensional subspaces of a vector space V as a subvariety of the projective space of the rth exterior power of that vector space, P....
do Grassmannians and flags over commutative fields. More information on these can be found in the survey article.
-
-
-
-
-
-
-
-
-
-

