Levi-Civita symbol
Overview
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
symbol, antisymmetric symbol, or alternating symbol, is a mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
symbol used in particular in tensor calculus. It is named after the Italian
Italian people
The Italian people are an ethnic group that share a common Italian culture, ancestry and speak the Italian language as a mother tongue. Within Italy, Italians are defined by citizenship, regardless of ancestry or country of residence , and are distinguished from people...
mathematician and physicist Tullio Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
.
In three dimensions, the Levi-Civita symbol is defined as follows:
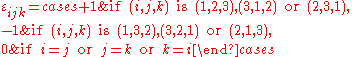
i.e.

