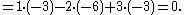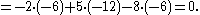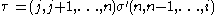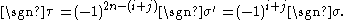Laplace expansion
Encyclopedia
In linear algebra
, the Laplace expansion, named after Pierre-Simon Laplace
, also called cofactor expansion, is an expression for the determinant
|B| of
an n × n square matrix
B that is a weighted sum of the determinants of n sub-matrices of B, each of size (n–1) × (n–1). The Laplace expansion is of theoretical interest as one of several ways to view the determinant, as well as of practical use in determinant computation.
The i, j cofactor
of B is the scalar Cij defined by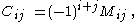
where Mij is the i, j minor
matrix of B, that is, the determinant of the (n–1) × (n–1) matrix that results from deleting the i-th row and the j-th column of B.
Then the Laplace expansion is given by the following
Theorem. Suppose B = (bij) is an n × n matrix and i, j ∈ {1, 2, ..., n}.
Then its determinant |B| is given by:
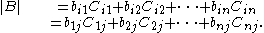
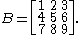
The determinant of this matrix can be computed by using the Laplace expansion along the first row: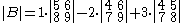
Alternatively, Laplace expansion along the second column yields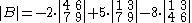
It is easy to see that the result is correct: the matrix is singular because the sum of its first and third column is twice the second column, and hence its determinant is zero.
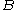 is an n × n matrix and
is an n × n matrix and 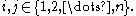 For clarity we also label the entries of
For clarity we also label the entries of 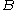 that compose its
that compose its 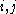 minor matrix
minor matrix 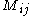 as
as
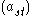 for
for 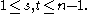
Consider the terms in the expansion of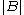 that have
that have 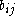 as a factor. Each has the form
as a factor. Each has the form
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Laplace expansion, named after Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, also called cofactor expansion, is an expression for the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
|B| of
an n × n square matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
B that is a weighted sum of the determinants of n sub-matrices of B, each of size (n–1) × (n–1). The Laplace expansion is of theoretical interest as one of several ways to view the determinant, as well as of practical use in determinant computation.
The i, j cofactor
Cofactor (linear algebra)
In linear algebra, the cofactor describes a particular construction that is useful for calculating both the determinant and inverse of square matrices...
of B is the scalar Cij defined by
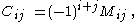
where Mij is the i, j minor
Minor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
matrix of B, that is, the determinant of the (n–1) × (n–1) matrix that results from deleting the i-th row and the j-th column of B.
Then the Laplace expansion is given by the following
Theorem. Suppose B = (bij) is an n × n matrix and i, j ∈ {1, 2, ..., n}.
Then its determinant |B| is given by:
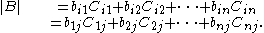
Examples
Consider the matrix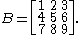
The determinant of this matrix can be computed by using the Laplace expansion along the first row:
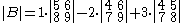
Alternatively, Laplace expansion along the second column yields
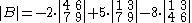
It is easy to see that the result is correct: the matrix is singular because the sum of its first and third column is twice the second column, and hence its determinant is zero.
Proof
Suppose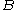 is an n × n matrix and
is an n × n matrix and 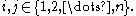 For clarity we also label the entries of
For clarity we also label the entries of  that compose its
that compose its 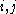 minor matrix
minor matrix 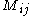 as
as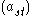 for
for 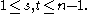
Consider the terms in the expansion of
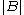 that have
that have 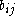 as a factor. Each has the form
as a factor. Each has the form-
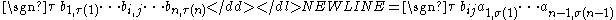
for some permutationEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
τ ∈ SSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
n with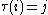 , and a unique and evidently related permutation
, and a unique and evidently related permutation 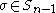 which selects the same minor entries as
which selects the same minor entries as 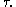 Similarly each choice of
Similarly each choice of  determines a corresponding
determines a corresponding 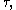 i.e. the correspondence
i.e. the correspondence  is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between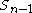 and
and 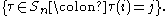 The permutation
The permutation  can be derived from
can be derived from  as follows.
as follows.
Define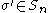 by
by 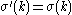 for
for 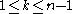 and
and 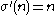 . Then
. Then 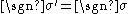 and
and
Since the two cyclesCycle notationIn combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles. This is also called circular notation and the permutation called a cyclic or circular permutation....
can be written respectively as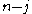 and
and 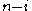 transpositions,
transpositions,
And since the map is bijective,
is bijective,
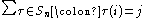
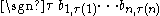
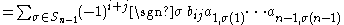
from which the result follows.
External links
- Laplace expansion at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
-