
Special unitary group
Encyclopedia
The special unitary group of degree n, denoted SU(n), is the group
of n×n unitary matrices
with determinant
1. The group operation is that of matrix multiplication
. The special unitary group is a subgroup
of the unitary group
U(n), consisting of all n×n unitary matrices, which is itself a subgroup of the general linear group
GL(n, C).
The SU(n) groups find wide application in the Standard Model
of particle physics
, especially SU(2) in the electroweak interaction
and SU(3) in QCD
.
The simplest case, SU(1), is the trivial group
, having only a single element. The group SU(2) is isomorphic to the group of quaternion
s of norm 1, and is thus diffeomorphic to the 3-sphere
. Since unit quaternions can be used to represent rotations in 3-dimensional space (up to sign), we have a surjective homomorphism
from SU(2) to the rotation group
SO(3) whose kernel
is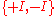 .
.
and simply connected. Algebraically, it is a simple Lie group
(meaning its Lie algebra
is simple; see below). The center of SU(n) is isomorphic to the cyclic group
Zn. Its outer automorphism group
, for n ≥ 3, is Z2, while the outer automorphism group of SU(2) is the trivial group
.
The Lie algebra
of SU(n), denoted by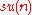 is generated by n² operators, which satisfy the commutator relationship (for i,j,k,l = 1, 2, ..., n)
is generated by n² operators, which satisfy the commutator relationship (for i,j,k,l = 1, 2, ..., n)
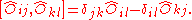
Additionally, the operator
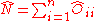
satisfies
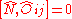
which implies that the number of independent generators is n²-1.
) of SU(n), T, are represented
as traceless
hermitian matrices. I.e:
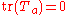
and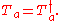
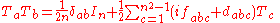
As a consequence: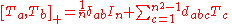
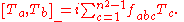
We also have
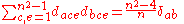
as a normalization convention.
the generators are represented by n²-1 × n²-1 matrices, n²-1 of them, whose elements are defined by the structure constants:
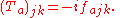
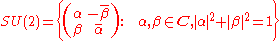
Now consider the following map:
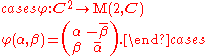
where denotes the set of 2 by 2 complex matrices. By considering
denotes the set of 2 by 2 complex matrices. By considering  diffeomorphic
diffeomorphic
to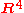 and
and 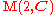 diffeomorphic to
diffeomorphic to 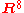 we can see that
we can see that 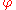 is an injective real linear map and hence an embedding. Now considering the restriction of
is an injective real linear map and hence an embedding. Now considering the restriction of  to the 3-sphere
to the 3-sphere
, denoted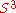 , we can see that this is an embedding of the 3-sphere onto a compact submanifold of
, we can see that this is an embedding of the 3-sphere onto a compact submanifold of  . However it is also clear that
. However it is also clear that  . Therefore as a manifold
. Therefore as a manifold  is diffeomorphic to SU(2) and so SU(2) is a compact, connected Lie group
is diffeomorphic to SU(2) and so SU(2) is a compact, connected Lie group
.
The Lie algebra
of SU(2) is:
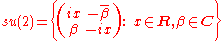
It is easily verified that matrices of this form have trace
zero and are antihermitian. The Lie algebra is then generated by the following matrices

which are easily seen to have the form of the general element specified above. These satisfy the relations and
and 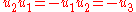 . The commutator bracket is therefore specified by
. The commutator bracket is therefore specified by
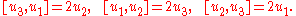
The above generators are related to the Pauli matrices
by ,
, 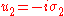 and
and  . This representation is often used in quantum mechanics
. This representation is often used in quantum mechanics
(see Pauli matrices
and Gell-Mann matrices
), to represent the spin
of fundamental particles such as electron
s. They also serve as unit vectors for the description of our 3 spatial dimensions in quantum relativity.
 (3), T, in the defining representation, are:
(3), T, in the defining representation, are:
where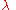 , the Gell-Mann matrices
, the Gell-Mann matrices
, are the SU(3) analog of the Pauli matrices
for SU(2):
Note that they span all traceless
Hermitian matrices as required.
These obey the relations
where the f are the structure constants, as previously defined, and have values given by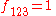

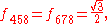
and all other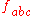 not related to these by permutation are zero.
not related to these by permutation are zero.
The d take the values: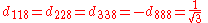
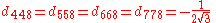
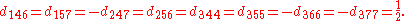
corresponding to SU(n) is denoted by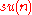 . Its standard mathematical representation consists of the traceless antihermitian
. Its standard mathematical representation consists of the traceless antihermitian 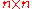 complex matrices, with the regular commutator
complex matrices, with the regular commutator
as Lie bracket
. A factor i is often inserted by particle
physicist
s, so that all matrices become Hermitian. This is simply a different, more convenient, representation of the same real Lie algebra. Note that is a Lie algebra over R.
is a Lie algebra over R.
If we choose an (arbitrary) particular basis, then the subspace
of traceless diagonal
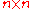 matrices with imaginary entries forms an
matrices with imaginary entries forms an  dimensional Cartan subalgebra.
dimensional Cartan subalgebra.
Complexify the Lie algebra, so that any traceless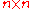 matrix is now allowed. The weight
matrix is now allowed. The weight
eigenvectors are the Cartan subalgebra itself and the matrices with only one nonzero entry which is off diagonal. Even though the Cartan subalgebra is only n - 1 dimensional, to simplify calculations, it is often convenient to introduce an auxiliary element, the unit matrix which commutes with everything else (which should not be thought of as an element of the Lie algebra!) for the purpose of computing weights and that only. So, we have a basis where the i-th basis vector is the matrix with 1 on the i-th diagonal entry and zero elsewhere. Weights would then be given by n coordinates and the sum over all n coordinates has to be zero (because the unit matrix is only auxiliary).
is only n - 1 dimensional, to simplify calculations, it is often convenient to introduce an auxiliary element, the unit matrix which commutes with everything else (which should not be thought of as an element of the Lie algebra!) for the purpose of computing weights and that only. So, we have a basis where the i-th basis vector is the matrix with 1 on the i-th diagonal entry and zero elsewhere. Weights would then be given by n coordinates and the sum over all n coordinates has to be zero (because the unit matrix is only auxiliary).
So, SU(n) is of rank
n - 1 and its Dynkin diagram is given by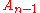 , a chain of
, a chain of  vertices. Its root system
vertices. Its root system
consists of n(n - 1) roots spanning a n - 1 Euclidean space
. Here, we use n redundant coordinates instead of n - 1 to emphasize the symmetries of the root system (the n coordinates have to add up to zero). In other words, we are embedding this n - 1 dimensional vector space in an n-dimensional one. Then, the roots consists of all the n(n - 1) permutations of (1, -1, 0, ..., 0). The construction given two paragraphs ago
explains why. A choice of simple root
s is
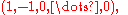
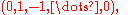
Its Cartan matrix
is
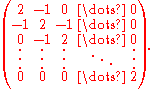
Its Weyl group
or Coxeter group
is the symmetric group
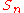 , the symmetry group
, the symmetry group
of the (n - 1)-simplex
.
F, the generalized special unitary group over F, SU(p,q;F), is the group
of all linear transformation
s of determinant
1 of a vector space
of rank n = p + q over F which leave invariant a nondegenerate, Hermitian form of signature (p, q). This group is often referred to as the special unitary group of signature p q over F. The field F can be replaced by a commutative ring
, in which case the vector space is replaced by a free module
.
Specifically, fix a Hermitian matrix A of signature p q in GL(n,R), then all
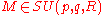
satisfy
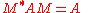
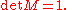
Often one will see the notation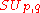 without reference to a ring or field, in this case the ring or field being referred to is C and this gives one of the classical Lie groups. The standard choice for A when F = C is
without reference to a ring or field, in this case the ring or field being referred to is C and this gives one of the classical Lie groups. The standard choice for A when F = C is
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of n×n unitary matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1. The group operation is that of matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. The special unitary group is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n), consisting of all n×n unitary matrices, which is itself a subgroup of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n, C).
The SU(n) groups find wide application in the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, especially SU(2) in the electroweak interaction
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
and SU(3) in QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
.
The simplest case, SU(1), is the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
, having only a single element. The group SU(2) is isomorphic to the group of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s of norm 1, and is thus diffeomorphic to the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. Since unit quaternions can be used to represent rotations in 3-dimensional space (up to sign), we have a surjective homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from SU(2) to the rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
SO(3) whose kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
is
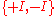 .
.Properties
The special unitary group SU(n) is a real matrix Lie group of dimension n² - 1. Topologically, it is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and simply connected. Algebraically, it is a simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
(meaning its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is simple; see below). The center of SU(n) is isomorphic to the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Zn. Its outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
, for n ≥ 3, is Z2, while the outer automorphism group of SU(2) is the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
.
The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SU(n), denoted by
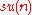 is generated by n² operators, which satisfy the commutator relationship (for i,j,k,l = 1, 2, ..., n)
is generated by n² operators, which satisfy the commutator relationship (for i,j,k,l = 1, 2, ..., n)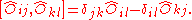
Additionally, the operator
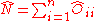
satisfies
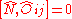
which implies that the number of independent generators is n²-1.
Generators
In general the infinitesimal generators (functions generative of the infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
) of SU(n), T, are represented
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
as traceless
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
hermitian matrices. I.e:
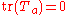
and
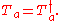
Fundamental representation
In the defining or fundamental representation the generators are represented by n×n matrices where: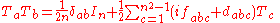
- where the f are the structure constants and are antisymmetric in all indices, whilst the d are symmetric in all indices.
As a consequence:
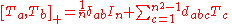
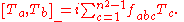
We also have
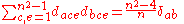
as a normalization convention.
Adjoint representation
In the adjoint representationAdjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
the generators are represented by n²-1 × n²-1 matrices, n²-1 of them, whose elements are defined by the structure constants:
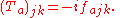
n=2
SU(2) is the following group: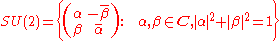
Now consider the following map:
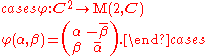
where
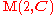 denotes the set of 2 by 2 complex matrices. By considering
denotes the set of 2 by 2 complex matrices. By considering 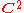 diffeomorphic
diffeomorphicDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to
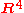 and
and 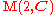 diffeomorphic to
diffeomorphic to 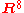 we can see that
we can see that 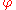 is an injective real linear map and hence an embedding. Now considering the restriction of
is an injective real linear map and hence an embedding. Now considering the restriction of  to the 3-sphere
to the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
, denoted
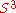 , we can see that this is an embedding of the 3-sphere onto a compact submanifold of
, we can see that this is an embedding of the 3-sphere onto a compact submanifold of  . However it is also clear that
. However it is also clear that  . Therefore as a manifold
. Therefore as a manifold  is diffeomorphic to SU(2) and so SU(2) is a compact, connected Lie group
is diffeomorphic to SU(2) and so SU(2) is a compact, connected Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SU(2) is:
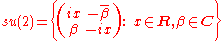
It is easily verified that matrices of this form have trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
zero and are antihermitian. The Lie algebra is then generated by the following matrices

which are easily seen to have the form of the general element specified above. These satisfy the relations
 and
and 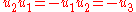 . The commutator bracket is therefore specified by
. The commutator bracket is therefore specified by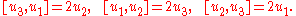
The above generators are related to the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
by
 ,
, 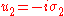 and
and  . This representation is often used in quantum mechanics
. This representation is often used in quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(see Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
and Gell-Mann matrices
Gell-Mann matrices
The Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
), to represent the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of fundamental particles such as electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s. They also serve as unit vectors for the description of our 3 spatial dimensions in quantum relativity.
n=3
The generators of (3), T, in the defining representation, are:
(3), T, in the defining representation, are:
where
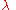 , the Gell-Mann matrices
, the Gell-Mann matricesGell-Mann matrices
The Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
, are the SU(3) analog of the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
for SU(2):
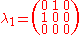 |
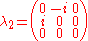 |
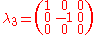 |
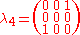 |
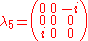 |
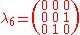 |
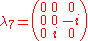 |
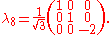 |
Note that they span all traceless
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
Hermitian matrices as required.
These obey the relations

where the f are the structure constants, as previously defined, and have values given by
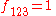

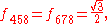
and all other
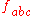 not related to these by permutation are zero.
not related to these by permutation are zero.The d take the values:
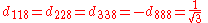
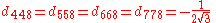
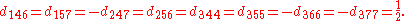
Lie algebra
The Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
corresponding to SU(n) is denoted by
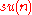 . Its standard mathematical representation consists of the traceless antihermitian
. Its standard mathematical representation consists of the traceless antihermitian 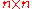 complex matrices, with the regular commutator
complex matrices, with the regular commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
as Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
. A factor i is often inserted by particle
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
s, so that all matrices become Hermitian. This is simply a different, more convenient, representation of the same real Lie algebra. Note that
 is a Lie algebra over R.
is a Lie algebra over R.If we choose an (arbitrary) particular basis, then the subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of traceless diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
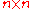 matrices with imaginary entries forms an
matrices with imaginary entries forms an  dimensional Cartan subalgebra.
dimensional Cartan subalgebra.Complexify the Lie algebra, so that any traceless
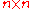 matrix is now allowed. The weight
matrix is now allowed. The weightWeight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
eigenvectors are the Cartan subalgebra itself and the matrices with only one nonzero entry which is off diagonal. Even though the Cartan subalgebra
 is only n - 1 dimensional, to simplify calculations, it is often convenient to introduce an auxiliary element, the unit matrix which commutes with everything else (which should not be thought of as an element of the Lie algebra!) for the purpose of computing weights and that only. So, we have a basis where the i-th basis vector is the matrix with 1 on the i-th diagonal entry and zero elsewhere. Weights would then be given by n coordinates and the sum over all n coordinates has to be zero (because the unit matrix is only auxiliary).
is only n - 1 dimensional, to simplify calculations, it is often convenient to introduce an auxiliary element, the unit matrix which commutes with everything else (which should not be thought of as an element of the Lie algebra!) for the purpose of computing weights and that only. So, we have a basis where the i-th basis vector is the matrix with 1 on the i-th diagonal entry and zero elsewhere. Weights would then be given by n coordinates and the sum over all n coordinates has to be zero (because the unit matrix is only auxiliary).So, SU(n) is of rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
n - 1 and its Dynkin diagram is given by
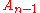 , a chain of
, a chain of  vertices. Its root system
vertices. Its root systemRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
consists of n(n - 1) roots spanning a n - 1 Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Here, we use n redundant coordinates instead of n - 1 to emphasize the symmetries of the root system (the n coordinates have to add up to zero). In other words, we are embedding this n - 1 dimensional vector space in an n-dimensional one. Then, the roots consists of all the n(n - 1) permutations of (1, -1, 0, ..., 0). The construction given two paragraphs ago
explains why. A choice of simple root
Simple root
in mathematics the term simple root can refer to one of two unrelated notions:*A simple root of a polynomial is a root of multiplicity one*A simple root in a root system is a member of a subset determined by a choice of positive roots...
s is
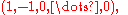
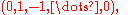
- …,

Its Cartan matrix
Cartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
is
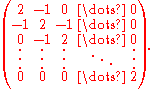
Its Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
or Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
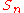 , the symmetry group
, the symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the (n - 1)-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
.
Generalized special unitary group
For a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, the generalized special unitary group over F, SU(p,q;F), is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1 of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of rank n = p + q over F which leave invariant a nondegenerate, Hermitian form of signature (p, q). This group is often referred to as the special unitary group of signature p q over F. The field F can be replaced by a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, in which case the vector space is replaced by a free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
.
Specifically, fix a Hermitian matrix A of signature p q in GL(n,R), then all
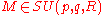
satisfy
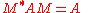
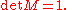
Often one will see the notation
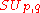 without reference to a ring or field, in this case the ring or field being referred to is C and this gives one of the classical Lie groups. The standard choice for A when F = C is
without reference to a ring or field, in this case the ring or field being referred to is C and this gives one of the classical Lie groups. The standard choice for A when F = C is
-

However there may be better choices for A for certain dimensions which exhibit more behaviour under restriction to subrings of C.
Example
A very important example of this type of group is the Picard modular group SU(2,1;Z[i]) which acts (projectively) on complex hyperbolic space of degree two, in the same way that SL(2,Z) acts (projectively) on real hyperbolic spaceHyperbolic spaceIn mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
of dimension two. In 2003 Gábor Francsics and Peter LaxPeter LaxPeter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...
computed a fundamental domain for the action of this group on , see.
, see.
Another example is SU(1,1;C) which is isomorphic to SL(2,R).
Important subgroups
In physics the special unitary group is used to represent bosonic symmetries. In theories of symmetry breakingSymmetry breakingSymmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
it is important to be able to find the subgroups of the special unitary group. Subgroups of SU(n) that are important in GUT physicsGrand unification theoryThe term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
are, for p>1, n-p>1: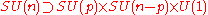 ,
,
where denotes the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
denotes the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
and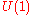 , known as the circle group, is the multiplicative group of all complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, known as the circle group, is the multiplicative group of all complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s with absolute value 1.
For completeness there are also the orthogonal and symplecticSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
subgroups: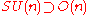

Since the rank of SU(n) is n-1 and of U(1) is 1, a useful check is that the sum of the ranks of the subgroups is less than or equal to the rank of the original group. SU(n) is a subgroup of various other lie groups: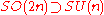
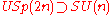
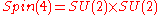 (see Spin group)
(see Spin group)
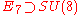
 (see Simple Lie groups for E6, E7, and G2).
(see Simple Lie groups for E6, E7, and G2).
There are also the identities SU(4)=Spin(6), SU(2)=Spin(3)=USp(2) and U(1)=Spin(2)=SO(2) .
One should finally mention that SU(2) is the double covering group of SO(3), a relation that plays an important role in the theory of rotations of 2-spinorSpinorIn mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s in non-relativistic quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
See also
- Representation theory of SU(2)Representation theory of SU(2)In the study of the representation theory of Lie groups, the study of representations of SU is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group and a non-abelian group...
- Projective special unitary group, PSU(n)
External links
- Representation theory of SU(2)

