
System of linear equations
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a system of linear equations (or linear system) is a collection of linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s involving the same set of variables. For example,

is a system of three equations in the three variables
 ,
, 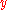 ,
,  .
.
Unanswered Questions

