In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, especially in set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment. Correspondingly, set B is a superset of A since all elements of A are also elements of B.

Definitions

If A and B are sets and every element of A is also an element of B, then:

• A is a subset of (or is included in) B, denoted by ,

or equivalently

• B is a superset of (or includes) A, denoted by

If A is a subset of B, but A is not equal to B (i.e. there exists at least one element of B not contained in A), then

• A is also a proper (or strict) subset of B; this is written as

or equivalently

• B is a proper superset of A; this is written as

For any set S, the inclusion relation

Relation (mathematics)

In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...

 ⊆ is a partial order on the set of all subsets of S (the power set of S).

The symbols ⊂ and ⊃

Some authors use the symbols ⊂ and ⊃ to indicate "subset" and "superset" respectively, instead of the symbols ⊆ and ⊇, but with the same meaning. So for example, for these authors, it is true of every set A that A ⊂ A.

Other authors prefer to use the symbols ⊂ and ⊃ to indicate proper subset and superset, respectively, in place of ⊊ and ⊋ This usage makes ⊆ and ⊂ analogous to the inequality symbols ≤ and <. For example, if x ≤ y then x may be equal to y, or maybe not, but if x < y, then x definitely does not equal y, but is strictly less than y. Similarly, using the "⊂ means proper subset" convention, if A ⊆ B, then A may or may not be equal to B, but if A ⊂ B, then A is definitely not equal to B.

Examples

• The set {1, 2} is a proper subset of {1, 2, 3}.
• Any set is a subset of itself, but not a proper subset.
• The empty set
  Empty set
  In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
  
  , denoted by ∅, is also a subset of any given set X. It also is always a proper subset, except of itself.
• The set {x: x is a prime number
  Prime number
  A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
  
   greater than 2000} is a proper subset of {x: x is an odd number greater than 1000}
• The set of natural number
  Natural number
  In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
  
  s is a proper subset of the set of rational number
  Rational number
  In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
  
  s and the set of points in a line segment
  Line segment
  In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
  
   is a proper subset of the set of points in a line
  Line (mathematics)
  The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
  
  . These are examples in which both the part and the whole are infinite, and the part has the same number of elements as the whole; such cases can tax intuition.

Other properties of inclusion

Inclusion is the canonical partial order in the sense that every partially ordered set (X, ) is isomorphic to some collection of sets ordered by inclusion. The ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

s are a simple example—if each ordinal n is identified with the set [n] of all ordinals less than or equal to n, then a ≤ b if and only if [a] ⊆ [b].

For the power set 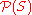 of a set S, the inclusion partial order is (up to an order isomorphism

Order isomorphism

In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...

) the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

 of k = |S| (the cardinality of S) copies of the partial order on {0,1} for which 0 < 1. This can be illustrated by enumerating S = {s₁, s₂, …, s_k} and associating with each subset T ⊆ S (which is to say with each element of 2^S) the k-tuple from {0,1}^k of which the ith coordinate is 1 if and only if s_i is a member of T.