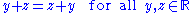Commutativity
Encyclopedia
In mathematics
an operation is commutative if changing the order of the operand
s does not change the end result. It is a fundamental property of many binary operations, and many mathematical proof
s depend on it. The commutativity of simple operations, such as multiplication and addition
of numbers, was for many years implicitly assumed and the property was not named until the 19th century when mathematics started to become formalized. By contrast, division
and subtraction
are not commutative.
s and functions
. Similarly, if the commutative property holds for a pair of elements under a certain binary operation then it is said that the two elements commute under that operation.
In group
and set theory
, many algebraic structures are called commutative when certain operands satisfy the commutative property. In higher branches of mathematics, such as analysis
and linear algebra
the commutativity of well known operations (such as addition
and multiplication
on real and complex numbers) is often used (or implicitly assumed) in proofs.
1. A binary operation
∗ on a set S is called commutative if:
An operation that does not satisfy the above property is called noncommutative.
2. One says that x commutes with y under ∗ if:
3. A binary function
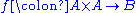 is called commutative if:
is called commutative if:
 Records of the implicit use of the commutative property go back to ancient times. The Egypt
Records of the implicit use of the commutative property go back to ancient times. The Egypt
ians used the commutative property of multiplication
to simplify computing products
. Euclid
is known to have assumed the commutative property of multiplication in his book Elements
. Formal uses of the commutative property arose in the late 18th and early 19th centuries, when mathematicians began to work on a theory of functions. Today the commutative property is a well known and basic property used in most branches of mathematics.
The first recorded use of the term commutative was in a memoir by François Servois in 1814, which used the word commutatives when describing functions that have what is now called the commutative property. The word is a combination of the French word commuter meaning "to substitute or switch" and the suffix -ative meaning "tending to" so the word literally means "tending to substitute or switch." The term then appeared in English in Philosophical Transactions of the Royal Society
in 1844.
For relations, a symmetric relation
is analogous to a commutative operation, in that if a relation R is symmetric, then .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
an operation is commutative if changing the order of the operand
Operand
In mathematics, an operand is the object of a mathematical operation, a quantity on which an operation is performed.-Example :The following arithmetic expression shows an example of operators and operands:3 + 6 = 9\;...
s does not change the end result. It is a fundamental property of many binary operations, and many mathematical proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
s depend on it. The commutativity of simple operations, such as multiplication and addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
of numbers, was for many years implicitly assumed and the property was not named until the 19th century when mathematics started to become formalized. By contrast, division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
and subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
are not commutative.
Common uses
The commutative property (or commutative law) is a property associated with binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s and functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. Similarly, if the commutative property holds for a pair of elements under a certain binary operation then it is said that the two elements commute under that operation.
In group
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, many algebraic structures are called commutative when certain operands satisfy the commutative property. In higher branches of mathematics, such as analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
the commutativity of well known operations (such as addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
on real and complex numbers) is often used (or implicitly assumed) in proofs.
Mathematical definitions
The term "commutative" is used in several related senses.1. A binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
∗ on a set S is called commutative if:

An operation that does not satisfy the above property is called noncommutative.
2. One says that x commutes with y under ∗ if:

3. A binary function
Binary function
In mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
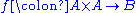 is called commutative if:
is called commutative if:
History and etymology

Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
ians used the commutative property of multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
to simplify computing products
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
. Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
is known to have assumed the commutative property of multiplication in his book Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
. Formal uses of the commutative property arose in the late 18th and early 19th centuries, when mathematicians began to work on a theory of functions. Today the commutative property is a well known and basic property used in most branches of mathematics.
The first recorded use of the term commutative was in a memoir by François Servois in 1814, which used the word commutatives when describing functions that have what is now called the commutative property. The word is a combination of the French word commuter meaning "to substitute or switch" and the suffix -ative meaning "tending to" so the word literally means "tending to substitute or switch." The term then appeared in English in Philosophical Transactions of the Royal Society
Philosophical Transactions of the Royal Society
The Philosophical Transactions of the Royal Society is a scientific journal published by the Royal Society of London. It was established in 1665, making it the first journal in the world exclusively devoted to science, and it has remained in continuous publication ever since, making it the world's...
in 1844.
Related properties

Associativity
The associative property is closely related to the commutative property. The associative property of an expression containing two or more occurrences of the same operator states that the order operations are performed in does not affect the final result, as long as the order of terms doesn't change. In contrast, the commutative property states that the order of the terms does not affect the final result.Symmetry
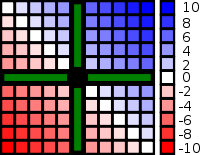
Symmetry can be directly linked to commutativity. When a commutative operator is written as a binary function then the resulting function is symmetric across the line y = x. As an example, if we let a function f represent addition (a commutative operation) so that f(x,y) = x + y then f is a symmetric function, which can be seen in the image on the right.For relations, a symmetric relation
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
is analogous to a commutative operation, in that if a relation R is symmetric, then
 .
.Commutative operations in everyday life
- Putting on socks resembles a commutative operation, since which sock is put on first is unimportant. Either way, the end result (having both socks on), is the same.
- The commutativity of addition is observed when paying for an item with cash. Regardless of the order the bills are handed over in, they always give the same total.
Commutative operations in mathematics
Two well-known examples of commutative binary operations are:- The additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, which is commutative since
-
- For example 4 + 5 = 5 + 4, since both expressionExpression (mathematics)In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
s equal 9.- The multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, which is commutative since
- The multiplication
- For example, 3 × 5 = 5 × 3, since both expressions equal 15.
- Further examples of commutative binary operations include addition and multiplication of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, addition and scalar multiplication of vectorsVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, and intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
and unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of sets.
Noncommutative operations in everyday life
- ConcatenationConcatenationIn computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
, the act of joining character strings together, is a noncommutative operation. For example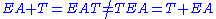
- Washing and drying clothes resembles a noncommutative operation; washing and then drying produces a markedly different result to drying and then washing.
- The twists of the Rubik's CubeRubik's CubeRubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
are noncommutative. This is studied in group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
Noncommutative operations in mathematics
Some noncommutative binary operations are:- SubtractionSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
is not commutative since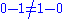
- DivisionDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
is noncommutative since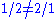
- MatrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
multiplication is noncommutative since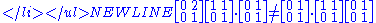
- The vector product (or cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
) of two vectors in three dimensions is anti-commutativeAnticommutativityIn mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...
, i.e., b × a = −(a × b).
Mathematical structures and commutativity
- A commutative semigroup is a set endowed with a total, associativeAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
and commutative operation. - If the operation additionally has an identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, we have a commutative monoid - An abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, or commutative group is a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
whose group operation is commutative. - A commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
is a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
whose multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
is commutative. (Addition in a ring is always commutative.) - In a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
both addition and multiplication are commutative.
Non-commuting operators in quantum mechanics
In quantum mechanicsIntroduction to quantum mechanicsQuantum mechanics is the body of scientific principles that explains the behavior of matter and its interactions with energy on the scale of atoms and atomic particles....
as formulated by SchrödingerErwin SchrödingerErwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
, physical variables are represented by linear operators such as x (meaning multiply by x), and d/dx. These two operators do not commute as may be seen by considering the effect of their products x(d/dx) and (d/dx)x on a one-dimensional wave function ψ(x):
-
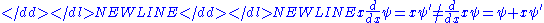
According to the uncertainty principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
of HeisenbergWerner HeisenbergWerner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
, if the two operators representing a pair of variables do not commute, then that pair of variables are mutually complementaryComplementarity (physics)In physics, complementarity is a basic principle of quantum theory proposed by Niels Bohr, closely identified with the Copenhagen interpretation, and refers to effects such as the wave–particle duality...
, which means they cannot be simultaneously measured or known precisely. For example, the position and the linear momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of a particle are represented respectively (in the x-direction) by the operators x and (ħ/i)d/dx (where ħ is the reduced Planck constantPlanck constantThe Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
). This is the same example except for the constant (ħ/i), so again the operators do not commute and the physical meaning is that the position and linear momentum in a given direction are complementary.
See also
- AnticommutativityAnticommutativityIn mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...
- Binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
- Commutant
- Commutative diagramCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
- Commutative (neurophysiology)Commutative (neurophysiology)In neurophysiology, commutation is the process of how the brain's neural circuits exhibit non-commutativity.Physiologist Douglas B. Tweed and coworkers consider whether certain neural circuits in the brain exhibit noncommutativity and state:...
- CommutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
- DistributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
- Particle statisticsParticle statisticsParticle statistics refers to the particular description of particles in statistical mechanics.-Classical statistics:In classical mechanics all the particles in the system are considered distinguishable. This means that one can label and track each individual particle in a system...
(for commutativity in physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
)
Books
- Abstract algebra theory. Covers commutativity in that context. Uses property throughout book.
- Abstract algebra theory. Uses commutativity property throughout book.
- Linear algebra theory. Explains commutativity in chapter 1, uses it throughout.
Articles
- http://www.ethnomath.org/resources/lumpkin1997.pdf Lumpkin, B. (1997). The Mathematical Legacy Of Ancient Egypt - A Response To Robert Palter. Unpublished manuscript.
- Article describing the mathematical ability of ancient civilizations.
- Robins, R. Gay, and Charles C. D. Shute. 1987. The Rhind Mathematical Papyrus: An Ancient Egyptian Text. London: British Museum Publications Limited. ISBN 0-7141-0944-4
- Translation and interpretation of the Rhind Mathematical PapyrusRhind Mathematical PapyrusThe Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
.
Online resources
- Krowne, Aaron, , Accessed 8 August 2007.
- Definition of commutativity and examples of commutative operations, Accessed 8 August 2007.
- Explanation of the term commute
- Yark. , Accessed 8 August 2007
- Examples proving some noncommutative operations
- O'Conner, J J and Robertson, E F. MacTutor history of real numbers, Accessed 8 August 2007
- Article giving the history of the real numbers
- Cabillón, Julio and Miller, Jeff. Earliest Known Uses Of Mathematical Terms, Accessed 22 November 2008
- Page covering the earliest uses of mathematical terms
- O'Conner, J J and Robertson, E F. MacTutor biography of François Servois, Accessed 8 August 2007
- Biography of Francois Servois, who first used the term
- Anticommutativity
- The vector product (or cross product