In
mathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, given two
groupsIn mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(
G, *) and (
H, ·), a
group homomorphism from
(
G, *) to (
H, ·) is a
functionIn mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
h :
G →
H such that for all
u and
v in
G it holds that
where the group operation on the left hand side of the equation is that of
G and on the right hand side that of
H.
From this property, one can deduce that
h maps the
identity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
eG of
G to the identity element
eH of
H, and it also maps inverses to inverses in the sense that
Hence one can say that
h "is compatible with the group structure".
Older notations for the homomorphism
h(
x) may be
xh, though this may be confused as an index or a general subscript.
A more recent trend is to write group homomorphisms on the right of their
arguments, omitting brackets, so that
h(
x) becomes simply
x h.
This approach is especially prevalent in areas of group theory where
automataAutomata is the plural form of automaton, a self-operating machine. It may also refer to:* "Automata", a short story by E. T. A. Hoffmann* "Automata", a hardboiled science fiction crime series by Penny Arcade...
play a role, since it accords better with the convention that automata read words from left to right.
In areas of mathematics where one considers groups endowed with additional structure, a
homomorphism sometimes means a map which respects not only the group structure (as above) but also the extra structure. For example, a homomorphism of
topological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s is often required to be continuous.
Intuition
The purpose of defining a group homomorphism as it is, is to create functions that preserve the algebraic structure. An equivalent definition of group homomorphism is: The function
h :
G →
H is a group homomorphism if whenever
we have
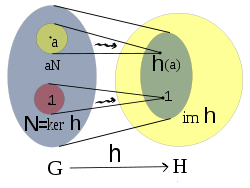
. In other words, the group
H in some sense has a similar algebraic structure as
G and the homomorphism
h preserves that.
Image and kernel
We define the
kernelIn the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of h to be the set of elements in
G which are mapped to the identity in
H
-
and the
imageIn mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of h to be
-
The kernel of h is a
normal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of
G (in fact,
h(
g-1 u g) =
h(
g)
-1 h(
u)
h(
g) =
h(
g)
-1 eH h(
g) =
h(
g)
-1 h(
g) =
eH) and the image of h is a
subgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of
H.
The homomorphism
h is injective (and called a
group monomorphism) if and only if ker(
h) = {
eG}.
The kernel and
imageIn mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
h(
G) = {
h(
g),
g ∈
G} of a homomorphism can be interpreted as measuring how close it is to being an isomorphism. The
First Isomorphism TheoremIn mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
states that the
imageIn mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a group homomorphism,
h(
G) is isomorphic to the quotient group
G/ker
h.
Examples
- Consider the cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z/3Z = {0, 1, 2} and the group of integers Z with addition. The map h : Z → Z/3Z with h(u) = u modIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
3 is a group homomorphism. It is surjective and its kernel consists of all integers which are divisible by 3.
- The exponential map
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
yields a group homomorphism from the group of real numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R with addition to the group of non-zero real numbers R* with multiplication. The kernel is {0} and the image consists of the positive real numbers.
- The exponential map also yields a group homomorphism from the group of complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C with addition to the group of non-zero complex numbers C* with multiplication. This map is surjective and has the kernel { 2πki : k in Z }, as can be seen from Euler's formula. Fields like R and C that have homomorphisms from their additive group to their multiplicative group are thus called exponential fieldIn mathematics, an exponential field is a field that has an extra operation on its elements which extends the usual idea of exponentiation.-Definition:...
s.
The category of groups
If
h :
G →
H and
k :
H →
K are group homomorphisms, then so is
k o
h :
G →
K. This shows that the class (in a sense of
category theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
) of all groups, together with group homomorphisms as morphisms, forms a
categoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Types of homomorphic maps
If the homomorphism
h is a
bijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
, then one can show that its inverse is also a group homomorphism, and
h is called a
group isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
; in this case, the groups
G and
H are called
isomorphic: they differ only in the notation of their elements and are identical for all practical purposes.
If
h:
G →
G is a group homomorphism, we call it an
endomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of
G. If furthermore it is bijective and hence an isomorphism, it is called an
automorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
. The set of all automorphisms of a group
G, with functional composition as operation, forms itself a group, the
automorphism group of
G. It is denoted by Aut(
G). As an example, the automorphism group of (
Z, +) contains only two elements, the identity transformation and multiplication with -1; it is isomorphic to
Z/2
Z.
An
epimorphism is a
surjectiveIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
homomorphism, that is, a homomorphism which is
onto as a function. A
monomorphism is an
injectiveIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
homomorphism, that is, a homomorphism which is
one-to-one as a function.
Homomorphisms of abelian groups
If
G and
H are
abelianIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(i.e. commutative) groups, then the set Hom(
G,
H) of all group homomorphisms from
G to
H is itself an abelian group: the sum
h +
k of two homomorphisms is defined by(
u) =
h(
u) +
k(
u) for all
u in
G.
The commutativity of
H is needed to prove that
h +
k is again a group homomorphism.
The addition of homomorphisms is compatible with the composition of homomorphisms in the following sense: if
f is in Hom(
K,
G),
h,
k are elements of Hom(
G,
H), and
g is in Hom(
H,
L), then o
f = (
h o
f) + (
k o
f) and
g o (
h +
k) = (
g o
h) + (
g o
k).
This shows that the set End(
G) of all endomorphisms of an abelian group forms a ring, the
endomorphism ringIn abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of
G. For example, the endomorphism ring of the abelian group consisting of the
direct sum of
m copies of
Z/
nZ is isomorphic to the ring of m-by-m
matricesIn mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries in
Z/n
Z. The above compatibility also shows that the category of all abelian groups with group homomorphisms forms a
preadditive categoryIn mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
; the existence of direct sums and well-behaved kernels makes this category the prototypical example of an
abelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.