
Rank (linear algebra)
Encyclopedia
The column rank of a matrix
A is the maximum number of linearly independent
column vectors of A. The row rank of a matrix
A is the maximum number of linearly independent
row vectors of A. Equivalently, the column rank of A is the dimension of the column space
of A, while the row rank of A is the dimension of the row space
of A.
A result of fundamental importance in linear algebra is that the column rank and the row rank are always equal (see below for proofs). This number (i.e. the number of linearly independent rows or columns) is simply called the rank of A. It is commonly denoted by either rk(A) or rank A. Since the column vectors of A are the row vectors of the transpose
of A (denoted here by AT), column rank of A equals row rank of A is equivalent to saying that the rank of a matrix is equal to the rank of its transpose, i.e. rk(A) = rk(AT).
The rank is also the dimension of the image of the linear transformation
that is multiplication by A. More generally, if a linear operator on a vector space
(possibly infinite-dimensional) has finite-dimensional range (e.g., a finite-rank operator), then the rank of the operator is defined as the dimension of the range.
The rank of an m × n matrix cannot be greater than m nor n. A matrix that has a rank as large as possible is said to have full rank; otherwise, the matrix is rank deficient.
. We present two proofs of this result. The first is short and uses only basic properties of linear combination
of vectors. The second is an elegant argument using orthogonality
and is based upon: Mackiw, G. (1995). A Note on the Equality of the Column and Row Rank of a Matrix. Mathematics Magazine, Vol. 68, No. 4. Interestingly, the first proof begins with a basis
for the column space
, while the second builds from a basis for the row space
. The first proof is valid when the matrices are defined over any field of scalars, while the second proof works only on inner-product spaces. Of course they both work for real and complex euclidean spaces. Also, the proofs are easily adapted when A is a linear transformation
.
First proof: Let be an
be an  ×
× matrix whose column rank is
matrix whose column rank is  . Therefore, the dimension of the column space
. Therefore, the dimension of the column space
of is
is  . Let
. Let  be any basis
be any basis
for the column space of and place them as column vectors to form the
and place them as column vectors to form the  ×
× matrix
matrix 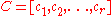 . From the definition of matrix multiplication
. From the definition of matrix multiplication
, it follows that each column vector of is a linear combination
is a linear combination
of the columns of
columns of  . This means that there exists an
. This means that there exists an  ×
× matrix
matrix  , such that
, such that 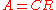 . (The
. (The 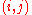 -th element of
-th element of  is the coefficient of
is the coefficient of  when the
when the  -th column of
-th column of  is expressed as a linear combination
is expressed as a linear combination
of the columns of
columns of  . Also see rank factorization
. Also see rank factorization
.)
Now, since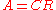 , every row vector of
, every row vector of  is a linear combination
is a linear combination
of the row vectors of , which means that the row space
, which means that the row space
of is contained within the row space of
is contained within the row space of  . Therefore, we have row rank of
. Therefore, we have row rank of  ≤ row rank of
≤ row rank of  . But note that
. But note that  has
has  rows, so the row rank of
rows, so the row rank of  ≤
≤  = column rank of
= column rank of  . This proves that row rank of
. This proves that row rank of  ≤ column rank of
≤ column rank of  . Now apply the result to the transpose of
. Now apply the result to the transpose of  to get the reverse inequality: column rank of
to get the reverse inequality: column rank of  = row rank of
= row rank of  ≤ column rank of
≤ column rank of  = row rank of
= row rank of  . This proves column rank of
. This proves column rank of  equals row rank of
equals row rank of  . See a very similar but more direct proof for rk(A) = rk(AT) under rank factorization
. See a very similar but more direct proof for rk(A) = rk(AT) under rank factorization
. QED.
Second proof: Let be an
be an  ×
× matrix whose row rank is
matrix whose row rank is  . Therefore, the dimension of the row space of
. Therefore, the dimension of the row space of  is
is  and suppose that
and suppose that  is a basis
is a basis
of the row space of . We claim that the vectors
. We claim that the vectors  are linearly independent. To see why, consider the linear homogeneous relation involving these vectors with scalar coefficients
are linearly independent. To see why, consider the linear homogeneous relation involving these vectors with scalar coefficients  :
: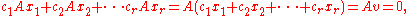
where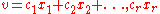 . We make two observations: (a)
. We make two observations: (a)  is a linear combination of vectors in the row space of
is a linear combination of vectors in the row space of  , which implies that
, which implies that  belongs to the row space of
belongs to the row space of  , and (b) since
, and (b) since  = 0,
= 0,  is orthogonal to every row vector of
is orthogonal to every row vector of  and, hence, is orthogonal to every vector in the row space of
and, hence, is orthogonal to every vector in the row space of  . The facts (a) and (b) together imply that
. The facts (a) and (b) together imply that  is orthogonal to itself, which proves that
is orthogonal to itself, which proves that  = 0 or, by the definition of
= 0 or, by the definition of  :
:
But recall that the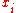 's are linearly independent because they are a basis of the row space of
's are linearly independent because they are a basis of the row space of  . This implies that
. This implies that  , which proves our claim that
, which proves our claim that 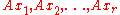 are linearly independent.
are linearly independent.
Now, each is obviously a vector in the column space of
is obviously a vector in the column space of  . So,
. So, 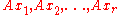 is a set of
is a set of  linearly independent vectors in the column space of
linearly independent vectors in the column space of  and, hence, the dimension of the column space of
and, hence, the dimension of the column space of  (i.e. the column rank of
(i.e. the column rank of  ) must be at least as big as
) must be at least as big as  . This proves that row rank of
. This proves that row rank of  = r ≤ column rank of
= r ≤ column rank of  . Now apply this result to the transpose of
. Now apply this result to the transpose of  to get the reverse inequality: column rank of
to get the reverse inequality: column rank of  = row rank of
= row rank of  ≤ column rank of
≤ column rank of  = row rank of
= row rank of  . This proves column rank of
. This proves column rank of  equals row rank of
equals row rank of  or, equivalently, rk(A) = rk(AT). QED.
or, equivalently, rk(A) = rk(AT). QED.
Finally, we provide a proof of the related result, rk(A) = rk(A*), where A* is the conjugate transpose
or hermitian transpose of A. When the elements of A are real numbers, this result becomes rk(A) = rk(AT) and can constitute another proof for row rank = column rank. Otherwise, for complex matrices, rk(A) = rk(A*) is not equivalent to row rank = column rank, and one of the above two proofs should be used. This proof is short, elegant and makes use of the null space
.
Third proof: Let A be an m×n matrix. Define rk(A) to mean the column rank of A and let A* denote the conjugate transpose
or hermitian transpose of A. First note that A*Ax = 0 if and only if Ax = 0. This is elementary linear algebra – one direction is trivial; the other follows from:
where ‖·‖ is the Euclidean norm. This proves that the null space
of A is equal to the null space
of A*A. From the rank-nullity theorem
, we obtain rk(A) = rk(A*A). (Alternate argument: Since A*Ax = 0 if and only if Ax = 0, the columns of A*A satisfy the same linear relationships as the columns of A. In particular, they must have the same number of linearly independent columns and, hence, the same column rank.) Each column of A*A is a linear combination of the columns of A*. Therefore, the column space of A*A is a subspace of the column space of A*. This implies that rk(A*A) ≤ rk(A*). We have proved: rk(A) = rk(A*A) ≤ rk(A*). Now apply this result to A* to obtain the reverse inequality: since (A*)* = A, we can write rk(A*) ≤ rk((A*)*) = rk(A). This proves rk(A) = rk(A*). When the elements of A are real, the conjugate transpose
is the transpose
and we obtain rk(A) = rk(AT). QED.
If one considers the matrix A as a linear mapping
such that
then the rank of A can also be defined as the dimension
of the image of f (see linear map for a discussion of image and kernel). This definition has the advantage that it can be applied to any linear map without need for a specific matrix. The rank can also be defined as n minus the dimension of the kernel
of f; the rank-nullity theorem
states that this is the same as the dimension of the image of f.
column rank – dimension of column space:
The maximal number of linearly independent columns of the m×n matrix A with entries in the field
of the m×n matrix A with entries in the field
F is equal to the dimension of the column space
of A (the column space being the subspace of Fm generated by the columns of A, which is in fact just the image of A as a linear map).
row rank – dimension of row space:
Since the column rank and the row rank are the same, we can also define the rank of A as the dimension of the row space
of A, or the number of rows in a basis of the row space.
in a basis of the row space.
decomposition rank:
The rank can also be characterized as the decomposition rank: the minimum k such that A can be factored as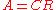 , where C is an m×k matrix and R is a k×n matrix. Like the "dimension of image" characterization this can be generalized to a definition of the rank of a linear map: the rank of a linear map f from V → W is the minimal dimension k of an intermediate space X such that f can be written as the composition of a map V → X and a map X → W. While this definition does not suggest an efficient manner to compute the rank (for which it is better to use one of the alternative definitions), it does allow to easily understand many of the properties of the rank, for instance that the rank of the transpose of A is the same as that of A. See rank factorization
, where C is an m×k matrix and R is a k×n matrix. Like the "dimension of image" characterization this can be generalized to a definition of the rank of a linear map: the rank of a linear map f from V → W is the minimal dimension k of an intermediate space X such that f can be written as the composition of a map V → X and a map X → W. While this definition does not suggest an efficient manner to compute the rank (for which it is better to use one of the alternative definitions), it does allow to easily understand many of the properties of the rank, for instance that the rank of the transpose of A is the same as that of A. See rank factorization
for details.
determinantal rank – size of largest non-vanishing minor:
Another equivalent definition of the rank of a matrix is the greatest order of any non-zero minor
in the matrix (the order of a minor being the size of the square sub-matrix of which it is the determinant). Like the decomposition rank characterization, this does not give an efficient way of computing the rank, but it is useful theoretically: a single non-zero minor witnesses a lower bound (namely its order) for the rank of the matrix, which can be useful to prove that certain operations do not lower the rank of a matrix.
Equivalence of the determinantal definition (rank of largest non-vanishing minor) is generally proved alternatively. It is a generalization of the statement that if the span of n vectors has dimension p, then p of those vectors span the space: one can choose a spanning set that is a subset of the vectors. For determinantal rank, the statement is that if the row rank (column rank) of a matrix is p, then one can choose a p × p submatrix that is invertible: a subset of the rows and a subset of the columns simultaneously define an invertible submatrix. It can be alternatively stated as: if the span of n vectors has dimension p, then p of these vectors span the space and there is a set of p coordinates on which they are linearly independent.
A non-vanishing p-minor (p × p submatrix with non-vanishing determinant) shows that the rows and columns of that submatrix are linearly independent, and thus those rows and columns of the full matrix are linearly independent (in the full matrix), so the row and column rank are at least as large as the determinantal rank; however, the converse is less straightforward.
tensor rank – minimum number of simple tensors:
The rank of a square matrix can also be characterized as the tensor rank: the minimum number of simple tensors (rank 1 tensors) needed to express A as a linear combination,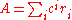 . Here a rank 1 tensor (matrix product of a column vector and a row vector) is the same thing as a rank 1 matrix of the given size. This interpretation can be generalized in the separable models interpretation of the singular value decomposition
. Here a rank 1 tensor (matrix product of a column vector and a row vector) is the same thing as a rank 1 matrix of the given size. This interpretation can be generalized in the separable models interpretation of the singular value decomposition
.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A is the maximum number of linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
column vectors of A. The row rank of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A is the maximum number of linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
row vectors of A. Equivalently, the column rank of A is the dimension of the column space
Column space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
of A, while the row rank of A is the dimension of the row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
of A.
A result of fundamental importance in linear algebra is that the column rank and the row rank are always equal (see below for proofs). This number (i.e. the number of linearly independent rows or columns) is simply called the rank of A. It is commonly denoted by either rk(A) or rank A. Since the column vectors of A are the row vectors of the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of A (denoted here by AT), column rank of A equals row rank of A is equivalent to saying that the rank of a matrix is equal to the rank of its transpose, i.e. rk(A) = rk(AT).
The rank is also the dimension of the image of the linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
that is multiplication by A. More generally, if a linear operator on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(possibly infinite-dimensional) has finite-dimensional range (e.g., a finite-rank operator), then the rank of the operator is defined as the dimension of the range.
The rank of an m × n matrix cannot be greater than m nor n. A matrix that has a rank as large as possible is said to have full rank; otherwise, the matrix is rank deficient.
Column rank = row rank or rk(A) = rk(AT)
This result forms a very important part of the fundamental theorem of linear algebraFundamental theorem of linear algebra
In mathematics, the fundamental theorem of linear algebra makes several statements regarding vector spaces. These may be stated concretely in terms of the rank r of an m×n matrix A and its singular value decomposition:A=U\Sigma V^T\...
. We present two proofs of this result. The first is short and uses only basic properties of linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of vectors. The second is an elegant argument using orthogonality
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
and is based upon: Mackiw, G. (1995). A Note on the Equality of the Column and Row Rank of a Matrix. Mathematics Magazine, Vol. 68, No. 4. Interestingly, the first proof begins with a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the column space
Column space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
, while the second builds from a basis for the row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
. The first proof is valid when the matrices are defined over any field of scalars, while the second proof works only on inner-product spaces. Of course they both work for real and complex euclidean spaces. Also, the proofs are easily adapted when A is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
.
First proof: Let
 be an
be an  ×
× matrix whose column rank is
matrix whose column rank is  . Therefore, the dimension of the column space
. Therefore, the dimension of the column spaceColumn space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
of
 is
is  . Let
. Let  be any basis
be any basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the column space of
 and place them as column vectors to form the
and place them as column vectors to form the  ×
× matrix
matrix 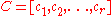 . From the definition of matrix multiplication
. From the definition of matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, it follows that each column vector of
 is a linear combination
is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the
 columns of
columns of  . This means that there exists an
. This means that there exists an  ×
× matrix
matrix  , such that
, such that 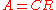 . (The
. (The 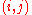 -th element of
-th element of  is the coefficient of
is the coefficient of  when the
when the  -th column of
-th column of  is expressed as a linear combination
is expressed as a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the
 columns of
columns of  . Also see rank factorization
. Also see rank factorizationRank factorization
Given an m \times n matrix A of rank r, a rank decomposition or rank factorization of A is a product A=CF, where C is an m \times r matrix and F is an r \times n matrix....
.)
Now, since
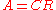 , every row vector of
, every row vector of  is a linear combination
is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the row vectors of
 , which means that the row space
, which means that the row spaceRow space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
of
 is contained within the row space of
is contained within the row space of  . Therefore, we have row rank of
. Therefore, we have row rank of  ≤ row rank of
≤ row rank of  . But note that
. But note that  has
has  rows, so the row rank of
rows, so the row rank of  ≤
≤  = column rank of
= column rank of  . This proves that row rank of
. This proves that row rank of  ≤ column rank of
≤ column rank of  . Now apply the result to the transpose of
. Now apply the result to the transpose of  to get the reverse inequality: column rank of
to get the reverse inequality: column rank of  = row rank of
= row rank of  ≤ column rank of
≤ column rank of  = row rank of
= row rank of  . This proves column rank of
. This proves column rank of  equals row rank of
equals row rank of  . See a very similar but more direct proof for rk(A) = rk(AT) under rank factorization
. See a very similar but more direct proof for rk(A) = rk(AT) under rank factorizationRank factorization
Given an m \times n matrix A of rank r, a rank decomposition or rank factorization of A is a product A=CF, where C is an m \times r matrix and F is an r \times n matrix....
. QED.
Second proof: Let
 be an
be an  ×
× matrix whose row rank is
matrix whose row rank is  . Therefore, the dimension of the row space of
. Therefore, the dimension of the row space of  is
is  and suppose that
and suppose that  is a basis
is a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the row space of
 . We claim that the vectors
. We claim that the vectors  are linearly independent. To see why, consider the linear homogeneous relation involving these vectors with scalar coefficients
are linearly independent. To see why, consider the linear homogeneous relation involving these vectors with scalar coefficients  :
: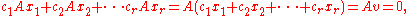
where
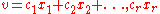 . We make two observations: (a)
. We make two observations: (a)  is a linear combination of vectors in the row space of
is a linear combination of vectors in the row space of  , which implies that
, which implies that  belongs to the row space of
belongs to the row space of  , and (b) since
, and (b) since  = 0,
= 0,  is orthogonal to every row vector of
is orthogonal to every row vector of  and, hence, is orthogonal to every vector in the row space of
and, hence, is orthogonal to every vector in the row space of  . The facts (a) and (b) together imply that
. The facts (a) and (b) together imply that  is orthogonal to itself, which proves that
is orthogonal to itself, which proves that  = 0 or, by the definition of
= 0 or, by the definition of  :
:
But recall that the
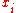 's are linearly independent because they are a basis of the row space of
's are linearly independent because they are a basis of the row space of  . This implies that
. This implies that  , which proves our claim that
, which proves our claim that 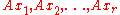 are linearly independent.
are linearly independent.Now, each
 is obviously a vector in the column space of
is obviously a vector in the column space of  . So,
. So, 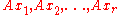 is a set of
is a set of  linearly independent vectors in the column space of
linearly independent vectors in the column space of  and, hence, the dimension of the column space of
and, hence, the dimension of the column space of  (i.e. the column rank of
(i.e. the column rank of  ) must be at least as big as
) must be at least as big as  . This proves that row rank of
. This proves that row rank of  = r ≤ column rank of
= r ≤ column rank of  . Now apply this result to the transpose of
. Now apply this result to the transpose of  to get the reverse inequality: column rank of
to get the reverse inequality: column rank of  = row rank of
= row rank of  ≤ column rank of
≤ column rank of  = row rank of
= row rank of  . This proves column rank of
. This proves column rank of  equals row rank of
equals row rank of  or, equivalently, rk(A) = rk(AT). QED.
or, equivalently, rk(A) = rk(AT). QED.Finally, we provide a proof of the related result, rk(A) = rk(A*), where A* is the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
or hermitian transpose of A. When the elements of A are real numbers, this result becomes rk(A) = rk(AT) and can constitute another proof for row rank = column rank. Otherwise, for complex matrices, rk(A) = rk(A*) is not equivalent to row rank = column rank, and one of the above two proofs should be used. This proof is short, elegant and makes use of the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
.
Third proof: Let A be an m×n matrix. Define rk(A) to mean the column rank of A and let A* denote the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
or hermitian transpose of A. First note that A*Ax = 0 if and only if Ax = 0. This is elementary linear algebra – one direction is trivial; the other follows from:
- A*Ax = 0 ⇒ x*A*Ax = 0 ⇒ (Ax)*(Ax) = 0 ⇒ ‖Ax‖2 = 0 ⇒ Ax = 0,
where ‖·‖ is the Euclidean norm. This proves that the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of A is equal to the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of A*A. From the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
, we obtain rk(A) = rk(A*A). (Alternate argument: Since A*Ax = 0 if and only if Ax = 0, the columns of A*A satisfy the same linear relationships as the columns of A. In particular, they must have the same number of linearly independent columns and, hence, the same column rank.) Each column of A*A is a linear combination of the columns of A*. Therefore, the column space of A*A is a subspace of the column space of A*. This implies that rk(A*A) ≤ rk(A*). We have proved: rk(A) = rk(A*A) ≤ rk(A*). Now apply this result to A* to obtain the reverse inequality: since (A*)* = A, we can write rk(A*) ≤ rk((A*)*) = rk(A). This proves rk(A) = rk(A*). When the elements of A are real, the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
is the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
and we obtain rk(A) = rk(AT). QED.
Alternative definitions
dimension of image:If one considers the matrix A as a linear mapping
- f : Fn → Fm
such that
- f(x) = Ax
then the rank of A can also be defined as the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the image of f (see linear map for a discussion of image and kernel). This definition has the advantage that it can be applied to any linear map without need for a specific matrix. The rank can also be defined as n minus the dimension of the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of f; the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
states that this is the same as the dimension of the image of f.
column rank – dimension of column space:
The maximal number of linearly independent columns
 of the m×n matrix A with entries in the field
of the m×n matrix A with entries in the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is equal to the dimension of the column space
Column space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
of A (the column space being the subspace of Fm generated by the columns of A, which is in fact just the image of A as a linear map).
row rank – dimension of row space:
Since the column rank and the row rank are the same, we can also define the rank of A as the dimension of the row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
of A, or the number of rows
 in a basis of the row space.
in a basis of the row space.decomposition rank:
The rank can also be characterized as the decomposition rank: the minimum k such that A can be factored as
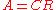 , where C is an m×k matrix and R is a k×n matrix. Like the "dimension of image" characterization this can be generalized to a definition of the rank of a linear map: the rank of a linear map f from V → W is the minimal dimension k of an intermediate space X such that f can be written as the composition of a map V → X and a map X → W. While this definition does not suggest an efficient manner to compute the rank (for which it is better to use one of the alternative definitions), it does allow to easily understand many of the properties of the rank, for instance that the rank of the transpose of A is the same as that of A. See rank factorization
, where C is an m×k matrix and R is a k×n matrix. Like the "dimension of image" characterization this can be generalized to a definition of the rank of a linear map: the rank of a linear map f from V → W is the minimal dimension k of an intermediate space X such that f can be written as the composition of a map V → X and a map X → W. While this definition does not suggest an efficient manner to compute the rank (for which it is better to use one of the alternative definitions), it does allow to easily understand many of the properties of the rank, for instance that the rank of the transpose of A is the same as that of A. See rank factorizationRank factorization
Given an m \times n matrix A of rank r, a rank decomposition or rank factorization of A is a product A=CF, where C is an m \times r matrix and F is an r \times n matrix....
for details.
determinantal rank – size of largest non-vanishing minor:
Another equivalent definition of the rank of a matrix is the greatest order of any non-zero minor
Minor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
in the matrix (the order of a minor being the size of the square sub-matrix of which it is the determinant). Like the decomposition rank characterization, this does not give an efficient way of computing the rank, but it is useful theoretically: a single non-zero minor witnesses a lower bound (namely its order) for the rank of the matrix, which can be useful to prove that certain operations do not lower the rank of a matrix.
Equivalence of the determinantal definition (rank of largest non-vanishing minor) is generally proved alternatively. It is a generalization of the statement that if the span of n vectors has dimension p, then p of those vectors span the space: one can choose a spanning set that is a subset of the vectors. For determinantal rank, the statement is that if the row rank (column rank) of a matrix is p, then one can choose a p × p submatrix that is invertible: a subset of the rows and a subset of the columns simultaneously define an invertible submatrix. It can be alternatively stated as: if the span of n vectors has dimension p, then p of these vectors span the space and there is a set of p coordinates on which they are linearly independent.
A non-vanishing p-minor (p × p submatrix with non-vanishing determinant) shows that the rows and columns of that submatrix are linearly independent, and thus those rows and columns of the full matrix are linearly independent (in the full matrix), so the row and column rank are at least as large as the determinantal rank; however, the converse is less straightforward.
tensor rank – minimum number of simple tensors:
The rank of a square matrix can also be characterized as the tensor rank: the minimum number of simple tensors (rank 1 tensors) needed to express A as a linear combination,
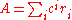 . Here a rank 1 tensor (matrix product of a column vector and a row vector) is the same thing as a rank 1 matrix of the given size. This interpretation can be generalized in the separable models interpretation of the singular value decomposition
. Here a rank 1 tensor (matrix product of a column vector and a row vector) is the same thing as a rank 1 matrix of the given size. This interpretation can be generalized in the separable models interpretation of the singular value decompositionSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
.
Properties
We assume that A is an m-by-n matrix over either the real numbers or the complex numbers, and we define the linear map f by f(x) = Ax as above.- only a zero matrix has rank zero.
-
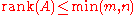
- f is injective if and only if A has rank n (in this case, we say that A has full column rank).
- f is surjective if and only if A has rank m (in this case, we say that A has full row rank).
- In the case of a square matrix A (i.e., m = n), then A is invertible if and only if A has rank n (that is, A has full rank).
- If B is any n-by-k matrix, then
-

- If B is an n-by-k matrix with rank n, then
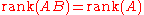
- If C is an l-by-m matrix with rank m, then

- The rank of A is equal to r if and only if there exists an invertible m-by-m matrix X and an invertible n-by-n matrix Y such that
-

- where Ir denotes the r-by-r identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.- Sylvester’s rank inequality: If A is a m-by-n matrix and B n-by-k, then
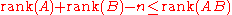 .
.
- This is a special case of the next inequality.
- The inequality due to Frobenius: if AB, ABC and BC are defined, then
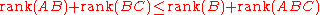 .
.
- Subadditivity:
 when A and B are of the same dimension. As a consequence, a rank-k matrix can be written as the sum of k rank-1 matrices, but not fewer.
when A and B are of the same dimension. As a consequence, a rank-k matrix can be written as the sum of k rank-1 matrices, but not fewer. - The rank of a matrix plus the nullity of the matrix equals the number of columns of the matrix (this is the "rank theorem" or the "rank-nullity theoremRank-nullity theoremIn mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
"). - The rank of a matrix and the rank of its corresponding Gram matrix are equal. Thus, for real matrices:
- Subadditivity:

- This can be shown by proving equality of their null spaces. Null space of the Gram matrix is given by vectors
 for which
for which  . If this condition is fulfilled, also holds
. If this condition is fulfilled, also holds  . This proof was adapted from.
. This proof was adapted from.
- If
 denotes the conjugate transpose of
denotes the conjugate transpose of  (i.e., the adjointHermitian adjointIn mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
(i.e., the adjointHermitian adjointIn mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of ), then
), then
 .
.
- If
Rank from row-echelon forms
A common approach to finding the rank of a matrix is to reduce it to a simpler form, generally row-echelon form by row operations. Row operations do not change the row space (hence do not change the row rank), and, being invertible, map the column space to an isomorphic space (hence do not change the column rank). Once in row-echelon form, the rank is clearly the same for both row rank and column rank, and equals the number of pivots (or basic columns) and also the number of non-zero rows, say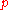 ; further, the column space has been mapped to
; further, the column space has been mapped to 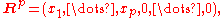 which has dimension
which has dimension 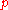 .
.
A potentially easier way to identify a matrices' rank is to use elementary row operationsElementary row operationsIn mathematics, an elementary matrix is a simple matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices...
to put the matrix in reduced row-echelon form and simply count the number of non-zero rows in the matrix. Below is an example of this process.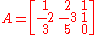
- Matrix
 can be put in reduced row-echelon form by using the following elementary row operations:
can be put in reduced row-echelon form by using the following elementary row operations: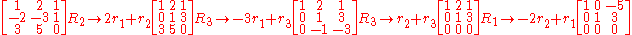
- By looking at the final matrix (reduced row-echelon form) one could see that the first non-zero entry in both
 and
and 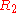 is a
is a 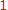 . Therefore the rank of matrix
. Therefore the rank of matrix  is 2.
is 2.
Computation
The easiest way to compute the rank of a matrix A is given by the Gauss elimination method. The row-echelon form of A produced by the Gauss algorithm has the same rank as A, and its rank can be read off as the number of non-zero rows.
Consider for example the 4-by-4 matrix
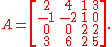
We see that the second column is twice the first column, and that the fourth column equals the sum of the first and the third. The first and the third columns are linearly independent, so the rank of A is two. This can be confirmed with the Gauss algorithm. It produces the following row echelon form of A:
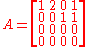
which has two non-zero rows.
When applied to floating pointFloating pointIn computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
computations on computers, basic Gaussian elimination (LU decompositionLU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
) can be unreliable, and a rank revealing decomposition should be used instead. An effective alternative is the singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
(SVD), but there are other less expensive choices, such as QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
with pivoting, which are still more numerically robust than Gaussian elimination. Numerical determination of rank requires a criterion for deciding when a value, such as a singular value from the SVD, should be treated as zero, a practical choice which depends on both the matrix and the application.
Applications
One useful application of calculating the rank of a matrix is the computation of the number of solutions of a system of linear equations. According to the Rouché–Capelli theoremRouché–Capelli theorem–Capelli theorem is the theorem in linear algebra that allows computing the number of solutions in a system of linear equations given the ranks of its augmented matrix and coefficient matrix...
, the system is inconsistent if the rank of the augmented matrixAugmented matrixIn linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...
is greater than the rank of the coefficient matrixCoefficient matrixIn linear algebra, the coefficient matrix refers to a matrix consisting of the coefficients of the variables in a set of linear equations.-Example:...
. If, on the other hand, ranks of these two matrices are equal, the system must have at least one solution. The solution is unique if and only if the rank equals the number of variables. Otherwise the general solution has k free parameters where k is the difference between the number of variables and the rank.
In control theoryControl theoryControl theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, the rank of a matrix can be used to determine whether a linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
is controllableControllabilityControllability is an important property of a control system, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control....
, or observableObservabilityObservability, in control theory, is a measure for how well internal states of a system can be inferred by knowledge of its external outputs. The observability and controllability of a system are mathematical duals. The concept of observability was introduced by American-Hungarian scientist Rudolf E...
.
Generalization
There are different generalisations of the concept of rank to matrices over arbitrary ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s. In those generalisations, column rank, row rank, dimension of column space and dimension of row space of a matrix may be different from the others or may not exist.
Thinking of matrices as tensors, the tensor rank generalizes to arbitrary tensors; note that for tensors of order greater than 2 (matrices are order 2 tensors), rank is very hard to compute, unlike for matrices.
There is a notion of rank for smooth maps between smooth manifolds. It is equal to the linear rank of the derivative.
Matrices as tensors
Matrix rank should not be confused with tensor order, which is called tensor rank. Tensor order is the number of indices required to write a tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, and thus matrices all have tensor order 2. More precisely, matrices are tensors of type (1,1), having one row index and one column index, also called covariant order 1 and contravariant order 1; see Tensor (intrinsic definition)Tensor (intrinsic definition)In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept...
for details.
Note that the tensor rank of a matrix can also mean the minimum number of simple tensors necessary to express the matrix as a linear combination, and that this definition does agree with matrix rank as here discussed.
Further reading
- Horn, Roger A. and Johnson, Charles R. Matrix Analysis. Cambridge University Press, 1985. ISBN 0-521-38632-2.
- Kaw, Autar K. Two Chapters from the book Introduction to Matrix Algebra: 1. Vectors http://numericalmethods.eng.usf.edu/mws/che/04sle/mws_che_sle_bck_vectors.pdf and System of Equations http://numericalmethods.eng.usf.edu/mws/che/04sle/mws_che_sle_bck_system.pdf
- Mike Brookes: Matrix Reference Manual. http://www.ee.ic.ac.uk/hp/staff/dmb/matrix/property.html#rank
- where Ir denotes the r-by-r identity matrix

