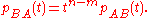Characteristic polynomial
Encyclopedia
In linear algebra
, one associates a polynomial
to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix
, most notably its eigenvalues, its determinant
and its trace
.
The characteristic polynomial of a graph
is the characteristic polynomial of its adjacency matrix
. It is a graph invariant, though it is not complete: the smallest pair of non-isomorphic graphs with the same characteristic polynomial have five nodes.
A, the characteristic polynomial is easy to define: if the diagonal entries are a1, a2, a3, etc. then the characteristic polynomial will be:

This works because the diagonal entries are also the eigenvalues of this matrix.
For a general matrix A, one can proceed as follows. A scalar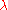 is an eigenvalue of A if and only if there is an eigenvector
is an eigenvalue of A if and only if there is an eigenvector  such that
such that
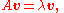
or
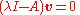
(where I is the identity matrix
). Since v is non-zero, this means that the matrix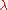 I − A is singular, which in turn means that its determinant
I − A is singular, which in turn means that its determinant
is 0 (non-invertible). Thus the roots of the function det(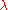 I − A) are the eigenvalues of A, and it is clear that this determinant is a polynomial in
I − A) are the eigenvalues of A, and it is clear that this determinant is a polynomial in 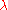 .
.
K (such as the real
or complex
numbers) and an n×n matrix A over K. The characteristic polynomial of A, denoted by pA(t), is the polynomial defined by
where I denotes the n-by-n identity matrix
and the determinant
is being taken in K[t], the ring of polynomials
in t over K.
(Some authors define the characteristic polynomial to be det(A − t I). That polynomial differs from the one defined here by a sign (−1)n, so it makes no difference for properties like having as roots the eigenvalues of A; however the current definition always gives a monic polynomial, whereas the alternative definition always has constant term det(A).)
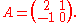
We have to compute the determinant
of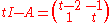
and the corresponding determinant
is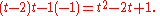
This is the characteristic polynomial of A.
of A, but its degree may be less than n). The coefficients of the characteristic polynomial are all polynomial expression
s in the entries of the matrix. In particular its constant coefficient is equal to (−1)ndet(A), and the coefficient of t n − 1 is equal to −tr(A), the matrix trace of A. For a 2×2 matrix A, the characteristic polynomial is therefore given by
The Cayley–Hamilton theorem
states that replacing t by A in the characteristic polynomial (interpreting the resulting powers as matrix powers, and the constant term c as c times the identity matrix) yields the zero matrix. Informally speaking, every matrix satisfies its own characteristic equation. This statement is equivalent to saying that the minimal polynomial
of A divides the characteristic polynomial of A.
Two similar matrices have the same characteristic polynomial. The converse however is not true in general: two matrices with the same characteristic polynomial need not be similar.
The matrix A and its transpose
have the same characteristic polynomial. A is similar to a triangular matrix
if and only if
its characteristic polynomial can be completely factored into linear factors over K (the same is true with the minimal polynomial instead of the characteristic polynomial). In this case A is similar to a matrix in Jordan normal form
.

More generally, if A is m×n-matrix and B is n×m matrices such that m<n, then AB is m×m and BA is n×n matrix.
One has
To prove the first result, recognize that the equation to be proved, as a polynomial in t and in the entries of A and B is a universal polynomial identity. It therefore suffices to check it on an open set of parameter values in the complex numbers. The tuples (A,B,t) where A is an invertible complex n by n matrix, B is any complex n by n matrix, and t is any complex number from an open set in complex space of dimension 2n2 + 1.
When A is non-singular our result follows from the fact that AB and BA are similar: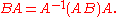
, the characteristic equation (or secular equation) of a square matrix
A is the equation in one variable λ
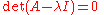
where det is the determinant
and I is the identity matrix
. The solutions of the characteristic equation are precisely the eigenvalues of the matrix A. The polynomial which results from evaluating the determinant is the characteristic polynomial of the matrix. The term "characteristic equation" is due to Wilhelm Killing
.
For example, the matrix
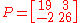
has characteristic equation
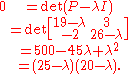
The eigenvalues of this matrix are therefore 20 and 25.
Some shortcuts exist for low dimension matrices. For a 2×2 matrix A, the characteristic polynomial can be found from its determinant
and trace
, tr(A), to be
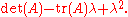
For a 3×3 matrix, we define c2 as the sum of the principal minors of the matrix, and find the characteristic polynomial to be

The Cayley–Hamilton theorem
states that every square matrix satisfies its own characteristic equation.
of a linear operator (in some literature the term secular function is still used). The term comes from the fact that these functions were used to calculate secular perturbations
(on a time scale of a century, i.e. slow compared to annual motion) of planetary orbits, according to Lagrange
's theory of oscillations.
In linear algebra
, zeros of a secular function are the eigenvalues of a matrix
. Characteristic polynomials also have eigenvalues as roots.
The characteristic polynomial is defined by the determinant
of the matrix with a shift. It has zeros only, without any pole. Commonly, the secular function implies the characteristic polynomial. But, in the strict sense, the secular function has poles as well. Interestingly, the poles are located in the eigenvalues of its sub-matrices. Thus, if the information of the sub-matrices is available, the eigenvalues of the matrix can be described using that kind of information. Furthermore, by partitioning the matrix like matrix tearing or gruing, we can iterate the eigenvalues in a recursive
way. According to the methods of partitioning, the variant forms of the secular functions can be built up. However, they are all of the form of a series of the simple rational functions, which have poles at the eigenvalues of the partitioned matrices. For example, we can find a form of secular function in the divide-and-conquer eigenvalue algorithm
.
Recently, the secular function has been utilized in signal processing
. The estimation problem with uncertainty involves a sort of eigenvalue problem, such as a bounded data uncertainty, total least squares, data least squares, partial least squares, errors-in-variables model
, etc. Many cases have been solved using their own secular equations. Some are still trying to find the unique secular equation that can resolve a given uncertainty estimation problem.
As for a numerical aspect, it is known that Newton's method
is delicate when finding the roots of the secular equation. The higher-order interpolations are recommended. Among them, a simple rational approximation
is a good choice considering the balance between the stability
and the computational complexity
. It is because the secular equation itself consists of a series of simple rational functions. However, using only interpolation cannot guarantee the stability. Thus fine search algorithms such as bisection steps are still required for accuracy.
In mathematics
and numerical analysis
it means characteristic equation.
In astronomy
it is the algebraic or numerical expression of the magnitude of the inequalities in a planet's motion that remain after the inequalities of a short period have been allowed for.
In molecular orbital
calculations relating to the energy of the electron and its wave function it is also used instead of the characteristic equation.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, one associates a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, most notably its eigenvalues, its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and its trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
.
The characteristic polynomial of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is the characteristic polynomial of its adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
. It is a graph invariant, though it is not complete: the smallest pair of non-isomorphic graphs with the same characteristic polynomial have five nodes.
Motivation
Given a square matrix A, we want to find a polynomial whose roots are precisely the eigenvalues of A. For a diagonal matrixDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
A, the characteristic polynomial is easy to define: if the diagonal entries are a1, a2, a3, etc. then the characteristic polynomial will be:

This works because the diagonal entries are also the eigenvalues of this matrix.
For a general matrix A, one can proceed as follows. A scalar
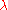 is an eigenvalue of A if and only if there is an eigenvector
is an eigenvalue of A if and only if there is an eigenvector  such that
such that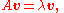
or
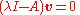
(where I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
). Since v is non-zero, this means that the matrix
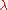 I − A is singular, which in turn means that its determinant
I − A is singular, which in turn means that its determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is 0 (non-invertible). Thus the roots of the function det(
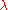 I − A) are the eigenvalues of A, and it is clear that this determinant is a polynomial in
I − A) are the eigenvalues of A, and it is clear that this determinant is a polynomial in 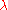 .
.Formal definition
We start with a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K (such as the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers) and an n×n matrix A over K. The characteristic polynomial of A, denoted by pA(t), is the polynomial defined by
- pA(t) = det(t I − A)
where I denotes the n-by-n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is being taken in K[t], the ring of polynomials
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in t over K.
(Some authors define the characteristic polynomial to be det(A − t I). That polynomial differs from the one defined here by a sign (−1)n, so it makes no difference for properties like having as roots the eigenvalues of A; however the current definition always gives a monic polynomial, whereas the alternative definition always has constant term det(A).)
Example
Suppose we want to compute the characteristic polynomial of the matrix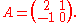
We have to compute the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of
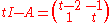
and the corresponding determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is
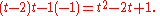
This is the characteristic polynomial of A.
Properties
The polynomial pA(t) is monic (its leading coefficient is 1) and its degree is n. The most important fact about the characteristic polynomial was already mentioned in the motivational paragraph: the eigenvalues of A are precisely the roots of pA(t) (this also holds for the minimal polynomialMinimal polynomial (linear algebra)
In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
of A, but its degree may be less than n). The coefficients of the characteristic polynomial are all polynomial expression
Polynomial expression
In mathematics, and in particular in the field of algebra, a polynomial expression in one or more given entities E1, E2, ..., is any meaningful expression constructed from copies of those entities together with constants, using the operations of addition and multiplication...
s in the entries of the matrix. In particular its constant coefficient is equal to (−1)ndet(A), and the coefficient of t n − 1 is equal to −tr(A), the matrix trace of A. For a 2×2 matrix A, the characteristic polynomial is therefore given by
- t 2 − tr(A)t + det(A).
The Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
states that replacing t by A in the characteristic polynomial (interpreting the resulting powers as matrix powers, and the constant term c as c times the identity matrix) yields the zero matrix. Informally speaking, every matrix satisfies its own characteristic equation. This statement is equivalent to saying that the minimal polynomial
Minimal polynomial (linear algebra)
In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
of A divides the characteristic polynomial of A.
Two similar matrices have the same characteristic polynomial. The converse however is not true in general: two matrices with the same characteristic polynomial need not be similar.
The matrix A and its transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
have the same characteristic polynomial. A is similar to a triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its characteristic polynomial can be completely factored into linear factors over K (the same is true with the minimal polynomial instead of the characteristic polynomial). In this case A is similar to a matrix in Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
.
Characteristic polynomial of a product of two matrices
If A and B are two square n×n matrices then characteristic polynomials of AB and BA coincide:
More generally, if A is m×n-matrix and B is n×m matrices such that m<n, then AB is m×m and BA is n×n matrix.
One has
To prove the first result, recognize that the equation to be proved, as a polynomial in t and in the entries of A and B is a universal polynomial identity. It therefore suffices to check it on an open set of parameter values in the complex numbers. The tuples (A,B,t) where A is an invertible complex n by n matrix, B is any complex n by n matrix, and t is any complex number from an open set in complex space of dimension 2n2 + 1.
When A is non-singular our result follows from the fact that AB and BA are similar:
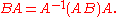
Characteristic equation
In linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the characteristic equation (or secular equation) of a square matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A is the equation in one variable λ
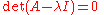
where det is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. The solutions of the characteristic equation are precisely the eigenvalues of the matrix A. The polynomial which results from evaluating the determinant is the characteristic polynomial of the matrix. The term "characteristic equation" is due to Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
.
For example, the matrix
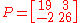
has characteristic equation
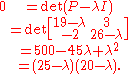
The eigenvalues of this matrix are therefore 20 and 25.
Some shortcuts exist for low dimension matrices. For a 2×2 matrix A, the characteristic polynomial can be found from its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, tr(A), to be
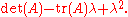
For a 3×3 matrix, we define c2 as the sum of the principal minors of the matrix, and find the characteristic polynomial to be

The Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
states that every square matrix satisfies its own characteristic equation.
Secular function
The term secular function has been used for what mathematicians now call a characteristic functionCharacteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of a linear operator (in some literature the term secular function is still used). The term comes from the fact that these functions were used to calculate secular perturbations
Secular phenomena
In astronomy, secular phenomena are contrasted with phenomena observed to repeat periodically. In particular, astronomical ephemerides use secular to label the longest-lasting or non-oscillatory perturbations in the motion of planets, as opposed to periodic perturbations which exhibit repetition...
(on a time scale of a century, i.e. slow compared to annual motion) of planetary orbits, according to Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
's theory of oscillations.
In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, zeros of a secular function are the eigenvalues of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Characteristic polynomials also have eigenvalues as roots.
The characteristic polynomial is defined by the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix with a shift. It has zeros only, without any pole. Commonly, the secular function implies the characteristic polynomial. But, in the strict sense, the secular function has poles as well. Interestingly, the poles are located in the eigenvalues of its sub-matrices. Thus, if the information of the sub-matrices is available, the eigenvalues of the matrix can be described using that kind of information. Furthermore, by partitioning the matrix like matrix tearing or gruing, we can iterate the eigenvalues in a recursive
Recursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
way. According to the methods of partitioning, the variant forms of the secular functions can be built up. However, they are all of the form of a series of the simple rational functions, which have poles at the eigenvalues of the partitioned matrices. For example, we can find a form of secular function in the divide-and-conquer eigenvalue algorithm
Divide-and-conquer eigenvalue algorithm
Divide-and-conquer eigenvalue algorithms are a class of eigenvalue algorithms for Hermitian or real symmetric matrices that have recently become competitive in terms of stability and efficiency with more traditional algorithms such as the QR algorithm. The basic concept behind these algorithms is...
.
Recently, the secular function has been utilized in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
. The estimation problem with uncertainty involves a sort of eigenvalue problem, such as a bounded data uncertainty, total least squares, data least squares, partial least squares, errors-in-variables model
Errors-in-variables model
Total least squares, also known as errors in variables, rigorous least squares, or orthogonal regression, is a least squares data modeling technique in which observational errors on both dependent and independent variables are taken into account...
, etc. Many cases have been solved using their own secular equations. Some are still trying to find the unique secular equation that can resolve a given uncertainty estimation problem.
As for a numerical aspect, it is known that Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
is delicate when finding the roots of the secular equation. The higher-order interpolations are recommended. Among them, a simple rational approximation
Simple rational approximation
Simple rational approximation is a subset of interpolating methods using rational functions. Especially, SRA interpolates a given function with a specific rational function whose poles and zeros are simple, which means that there is no multiplicity in poles and zeros. Sometimes, it only implies...
is a good choice considering the balance between the stability
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
and the computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
. It is because the secular equation itself consists of a series of simple rational functions. However, using only interpolation cannot guarantee the stability. Thus fine search algorithms such as bisection steps are still required for accuracy.
Secular equation
Secular equation has several meanings.In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
it means characteristic equation.
In astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
it is the algebraic or numerical expression of the magnitude of the inequalities in a planet's motion that remain after the inequalities of a short period have been allowed for.
In molecular orbital
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
calculations relating to the energy of the electron and its wave function it is also used instead of the characteristic equation.