
Hopf algebra
Encyclopedia
In mathematics
, a Hopf algebra, named after Heinz Hopf
, is a structure that is simultaneously an (unital associative) algebra
and a (counital coassociative) coalgebra
, with these structures' compatibility making it a bialgebra
, and that moreover is equipped with an antiautomorphism satisfying a certain property.
Hopf algebras occur naturally in algebraic topology
, where they originated and are related to the H-space
concept, in group scheme
theory, in group theory
(via the concept of a group ring
), and in numerous other places, making them probably the most familiar type of bialgebra
. Hopf algebras are also studied in their own right, with much work on specific classes of examples on the one hand and classification problems on the other.
H over a field
K together with a K-linear
map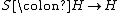 (called the antipode) such that the following diagram commutes
(called the antipode) such that the following diagram commutes
:
Here Δ is the comultiplication of the bialgebra, ∇ its multiplication, η its unit and ε its counit. In the sumless Sweedler notation, this property can also be expressed as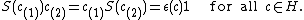
As for algebra
s, one can replace the underlying field K with a commutative ring
R in the above definition.
The definition of Hopf algebra is self-dual
(as reflected in the symmetry of the above diagram), so if one can define a dual
of H (which is always possible if H is finite-dimensional), then it is automatically a Hopf algebra.
In general, S is an antihomomorphism
, so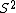 is a homomorphism
is a homomorphism
, which is therefore an automorphism if S was invertible (as may be required).
If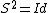 , then the Hopf algebra is said to be involutive (and the underlying algebra with involution is a *-algebra). If H is finite-dimensional semisimple over a field of characteristic zero, commutative, or cocommutative, then it is involutive.
, then the Hopf algebra is said to be involutive (and the underlying algebra with involution is a *-algebra). If H is finite-dimensional semisimple over a field of characteristic zero, commutative, or cocommutative, then it is involutive.
If a bialgebra B admits an antipode S, then S is unique ("a bialgebra admits at most 1 Hopf algebra structure").
The antipode is an analog to the inversion map on a group that sends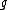 to
to  .
.
A Hopf subalgebra K is said to be right normal in a Hopf algebra H if it satisfies the condition of stability,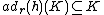 for all h in H,
for all h in H,
where the right adjoint mapping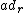 is defined by
is defined by  for all k in K, h in H. Similarly, a Hopf subalgebra K is left normal in H if
for all k in K, h in H. Similarly, a Hopf subalgebra K is left normal in H if
it is stable under the left adjoint mapping defined by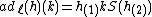 . The two conditions of normality are equivalent if the antipode S is bijective, in which case K is said to be a normal Hopf subalgebra.
. The two conditions of normality are equivalent if the antipode S is bijective, in which case K is said to be a normal Hopf subalgebra.
A normal Hopf subalgebra K in H satisfies the condition (of equality of subsets of H):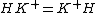 where
where  denotes the kernel of the counit on K. This normality condition implies that
denotes the kernel of the counit on K. This normality condition implies that 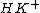 is a Hopf ideal of H (i.e. an algebra ideal in the kernel of the counit, a coalgebra coideal and stable under the antipode). As a consequence one has a quotient Hopf algebra
is a Hopf ideal of H (i.e. an algebra ideal in the kernel of the counit, a coalgebra coideal and stable under the antipode). As a consequence one has a quotient Hopf algebra 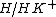 and epimorphism
and epimorphism 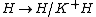 , a theory analogous to that of normal subgroups and quotient groups in group theory
, a theory analogous to that of normal subgroups and quotient groups in group theory
.
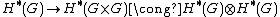
by the group multiplication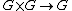 .
.
This observation was actually a source of the notion of Hopf algebra. Using this structure, Hopf proved a structure theorem for the cohomology algebra of Lie groups.
Theorem (Hopf) Let A be a finite-dimensional, graded commutative, graded
cocommutative Hopf algebra over a field of characteristic 0. Then A (as an algebra) is a free exterior algebra with generators of odd degree.
 Δ where T: H ⊗ H → H ⊗ H is defined by T(x ⊗ y) = y ⊗ x). Other interesting Hopf algebras are certain "deformations" or "quantization
Δ where T: H ⊗ H → H ⊗ H is defined by T(x ⊗ y) = y ⊗ x). Other interesting Hopf algebras are certain "deformations" or "quantization
s" of those from example 3 which are neither commutative nor co-commutative. These Hopf algebras are often called quantum groups, a term that is so far only loosely defined. They are important in noncommutative geometry
, the idea being the following: a standard algebraic group is well described by its standard Hopf algebra of regular functions; we can then think of the deformed version of this Hopf algebra as describing a certain "non-standard" or "quantized" algebraic group (which is not an algebraic group at all). While there does not seem to be a direct way to define or manipulate these non-standard objects, one can still work with their Hopf algebras, and indeed one identifies them with their Hopf algebras. Hence the name "quantum group".
Hopf algebras are often used in algebraic topology
: they are the natural algebraic structure on the direct sum of all homology
or cohomology
groups of an H-space
.
Locally compact quantum group
s generalize Hopf algebras and carry a topology
. The algebra of all continuous function
s on a Lie group
is a locally compact quantum group.
Quasi-Hopf algebras are generalizations of Hopf algebras, where coassociativity only holds up to a twist.
Weak Hopf algebras, or quantum groupoids, are generalizations of Hopf algebras. Like
Hopf algebras, weak Hopf algebras form a self-dual class of algebras; i.e., if H is a (weak) Hopf algebra, so is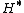 , the dual space of linear forms on H (with respect to the algebra-coalgebra structure obtained from the natural pairing with H and its coalgebra-algebra structure).
, the dual space of linear forms on H (with respect to the algebra-coalgebra structure obtained from the natural pairing with H and its coalgebra-algebra structure).
A weak Hopf algebra H is usually taken to be a 1) finite dimensional algebra and coalgebra with coproduct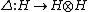 and counit
and counit 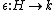
satisfying all the axioms of Hopf algebra except possibly or
or 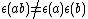
for some a,b in H. Instead one requires that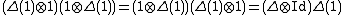 and
and 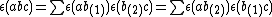
for all a,b, and c in H.
2) H has a weakened antipode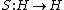 satisfying the axioms (a) - (c): (a)
satisfying the axioms (a) - (c): (a) 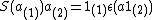 for all a in H (the right-hand side is the interesting
for all a in H (the right-hand side is the interesting
projection usually denoted by or
or 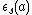
with image a separable subalgebra denoted by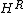 or
or  ); (b)
); (b) 
for all a in H (another interesting projection usually denoted by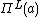 or
or 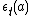
with image a separable algebra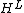 or
or 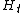 , anti-isomorphic to
, anti-isomorphic to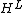 via S); and (c)
via S); and (c) 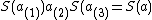
for all a in H. Note that if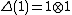 , these conditions reduce to the two usual conditions on the antipode of a Hopf algebra.
, these conditions reduce to the two usual conditions on the antipode of a Hopf algebra.
The axioms are partly chosen so that the category of H-modules is a rigid tensor category.
The unit H-module is the separable algebra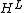 mentioned above.
mentioned above.
For example, a finite groupoid
algebra is a weak Hopf algebra. In particular, the groupoid
algebra on [n] with one pair of invertible arrows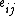 and
and  between i and j in [n] is isomorphic to the algebra H of n x n matrices. The weak Hopf algebra structure on this particular H is given by coproduct
between i and j in [n] is isomorphic to the algebra H of n x n matrices. The weak Hopf algebra structure on this particular H is given by coproduct 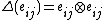 , counit
, counit  and antipode
and antipode 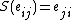 .
.
The separable subalgebras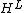 and
and 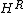 coincide and are non-central commutative algebras in this particular case (the subalgebra of diagonal matrices).
coincide and are non-central commutative algebras in this particular case (the subalgebra of diagonal matrices).
Early theoretical contributions to weak Hopf algebras are to be found in as well as
Hopf algebroids introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry (later shown equivalent in nontrivial way to a construction of Takeuchi from the 1970s and another by Xu around the year 2000): Hopf algebroids generalize weak Hopf algebras and certain skew Hopf algebras. They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras
become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely
a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra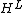 .
.
The antipode axioms have been changed by G. Böhm and K. Szlachanyi (J. Algebra) in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra
extensions.
A left Hopf algebroid (H,R) is a left bialgebroid together with an antipode: the bialgebroid (H,R)
consists of a total algebra H and a base algebra R and two mappings, an algebra
homomorphism called a source map, an algebra anti-homomorphism
called a source map, an algebra anti-homomorphism  called a target map, such that the commutativity condition
called a target map, such that the commutativity condition  is satisfied for all
is satisfied for all 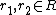 . The axioms resemble those of a Hopf algebra but are complicated by the possibility that R is a noncommutative algebra or its images under s and t are not in the center of H. In particular a left bialgebroid (H,R) has an R-R-bimodule structure on H which prefers the left side as follows:
. The axioms resemble those of a Hopf algebra but are complicated by the possibility that R is a noncommutative algebra or its images under s and t are not in the center of H. In particular a left bialgebroid (H,R) has an R-R-bimodule structure on H which prefers the left side as follows: 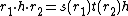 for all h in H,
for all h in H, 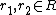 . There is a coproduct
. There is a coproduct
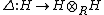 and counit
and counit 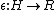
that make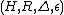 an R-coring (with axioms like that of a coalgebra
an R-coring (with axioms like that of a coalgebra
such that all mappings are R-R-bimodule homomorphisms and all tensors over R). Additionally the bialgebroid (H,R) must satisfy
 for all a,b in H, and a condition to make sure this last condition makes sense: every image point
for all a,b in H, and a condition to make sure this last condition makes sense: every image point 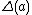 satisfies
satisfies 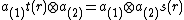 for all r in R. Also
for all r in R. Also 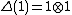 . The counit is required to satisfy
. The counit is required to satisfy 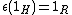 and the condition
and the condition 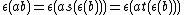 .
.
The antipode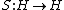 is usually taken to be an algebra anti-automorphism satisfying conditions of exchanging the source and target maps and satisfying two axioms like Hopf algebra antipode axioms; see the references in Lu or in Böhm-Szlachanyi for a more example-category friendly, though somewhat more complicated, set of axioms for the antipode S.
is usually taken to be an algebra anti-automorphism satisfying conditions of exchanging the source and target maps and satisfying two axioms like Hopf algebra antipode axioms; see the references in Lu or in Böhm-Szlachanyi for a more example-category friendly, though somewhat more complicated, set of axioms for the antipode S.
The latter set of axioms depend on the axioms of a right bialgebroid as well, which are a straightforward switching of left to right, s with t, of the axioms for a left bialgebroid given above.
As an example of left bialgebroid, take R to be any algebra over a field k. Let H be its algebra of linear self-mappings. Let s(r) be left multication by r on R; let t(r) be right multiplication by r on R. H is a left bialgebroid over R, which may be seen as follows.
From the fact that one may define a coproduct by
one may define a coproduct by
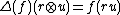 for each linear transformation f from R to itself
for each linear transformation f from R to itself
and all r,u in R. Coassociativity of the coproduct follows from associativity of the product on R. A counit is given by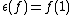 . The counit axioms of a coring follow from the identity element condition on multiplication in R. The reader will be amused, or at least edified, to check that (H,R) is a left bialgebroid. In case R is an Azumaya algebra, in which case
. The counit axioms of a coring follow from the identity element condition on multiplication in R. The reader will be amused, or at least edified, to check that (H,R) is a left bialgebroid. In case R is an Azumaya algebra, in which case
H is isomorphic to R tensor R, an antipode comes from transposing tensors, which makes H a Hopf algebroid over R.
Multiplier Hopf algebras introduced by Alfons Van Daele in 1994 are generalizations of Hopf algebras where comultiplication from an algebra (with or withthout unit) to the
multiplier algebra
of tensor product algebra of the algebra with itself.
Hopf group-(co)algebras introduced by V.G.Turaev in 2000 are also generalizations of Hopf algebras.
In this philosophy, a group can be thought of as a Hopf algebra over the "field with one element
".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hopf algebra, named after Heinz Hopf
Heinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
, is a structure that is simultaneously an (unital associative) algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
and a (counital coassociative) coalgebra
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
, with these structures' compatibility making it a bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
, and that moreover is equipped with an antiautomorphism satisfying a certain property.
Hopf algebras occur naturally in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, where they originated and are related to the H-space
H-space
In mathematics, an H-space is a topological space X together with a continuous map μ : X × X → X with an identity element e so that μ = μ = x for all x in X...
concept, in group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
theory, in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
(via the concept of a group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
), and in numerous other places, making them probably the most familiar type of bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
. Hopf algebras are also studied in their own right, with much work on specific classes of examples on the one hand and classification problems on the other.
Formal definition
Formally, a Hopf algebra is a (associative and coassociative) bialgebraBialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
H over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K together with a K-linear
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
map
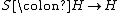 (called the antipode) such that the following diagram commutes
(called the antipode) such that the following diagram commutesCommutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
Here Δ is the comultiplication of the bialgebra, ∇ its multiplication, η its unit and ε its counit. In the sumless Sweedler notation, this property can also be expressed as
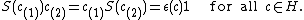
As for algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s, one can replace the underlying field K with a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R in the above definition.
The definition of Hopf algebra is self-dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
(as reflected in the symmetry of the above diagram), so if one can define a dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of H (which is always possible if H is finite-dimensional), then it is automatically a Hopf algebra.
Properties of the antipode
The antipode S is sometimes required to have a K-linear inverse, which is automatic in the finite-dimensional case, or if H is commutative or cocommutative (or more generally quasitriangular).In general, S is an antihomomorphism
Antihomomorphism
In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to...
, so
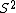 is a homomorphism
is a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
, which is therefore an automorphism if S was invertible (as may be required).
If
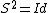 , then the Hopf algebra is said to be involutive (and the underlying algebra with involution is a *-algebra). If H is finite-dimensional semisimple over a field of characteristic zero, commutative, or cocommutative, then it is involutive.
, then the Hopf algebra is said to be involutive (and the underlying algebra with involution is a *-algebra). If H is finite-dimensional semisimple over a field of characteristic zero, commutative, or cocommutative, then it is involutive.If a bialgebra B admits an antipode S, then S is unique ("a bialgebra admits at most 1 Hopf algebra structure").
The antipode is an analog to the inversion map on a group that sends
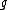 to
to  .
.Hopf subalgebras
A subalgebra K (not to be confused with the Field K in the notation above) of a Hopf algebra H is a Hopf subalgebra if it is a subcoalgebra of H and the antipode S maps K into K. In other words, a Hopf subalgebra K is a Hopf algebra in its own right when the multiplication, comultiplication, counit and antipode of H is restricted to K (and additionally the identity 1 is required to be in K). The Nichols-Zoeller Freeness theorem established (in 1989) that either natural K-module H is free of finite rank if H is finite dimensional: a generalization of Lagrange's theorem for subgroups. As a corollary of this and integral theory, a Hopf subalgebra of a semisimple finite dimensional Hopf algebra is automatically semisimple.A Hopf subalgebra K is said to be right normal in a Hopf algebra H if it satisfies the condition of stability,
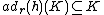 for all h in H,
for all h in H,where the right adjoint mapping
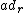 is defined by
is defined by  for all k in K, h in H. Similarly, a Hopf subalgebra K is left normal in H if
for all k in K, h in H. Similarly, a Hopf subalgebra K is left normal in H ifit is stable under the left adjoint mapping defined by
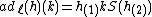 . The two conditions of normality are equivalent if the antipode S is bijective, in which case K is said to be a normal Hopf subalgebra.
. The two conditions of normality are equivalent if the antipode S is bijective, in which case K is said to be a normal Hopf subalgebra.A normal Hopf subalgebra K in H satisfies the condition (of equality of subsets of H):
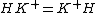 where
where  denotes the kernel of the counit on K. This normality condition implies that
denotes the kernel of the counit on K. This normality condition implies that 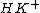 is a Hopf ideal of H (i.e. an algebra ideal in the kernel of the counit, a coalgebra coideal and stable under the antipode). As a consequence one has a quotient Hopf algebra
is a Hopf ideal of H (i.e. an algebra ideal in the kernel of the counit, a coalgebra coideal and stable under the antipode). As a consequence one has a quotient Hopf algebra 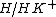 and epimorphism
and epimorphism 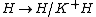 , a theory analogous to that of normal subgroups and quotient groups in group theory
, a theory analogous to that of normal subgroups and quotient groups in group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
Examples
- Group algebra. Suppose G is a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. The group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
KG is a unital associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over K. It turns into a Hopf algebra if we define- Δ : KG → KG ⊗ KG by Δ(g) = g ⊗ g for all g in G
- ε : KG → K by ε(g) = 1 for all g in G
- S : KG → KG by S(g) = g −1 for all g in G.
- The Hopf algebra KG is commutative if and only if the group is commutative; it is always co-commutative (see below).
- Functions on a finite group. Suppose now that G is a finite group. Then the set KG of all functions from G to K with pointwise addition and multiplication is a unital associative algebra over K, and KG ⊗ KG is naturally isomorphic to KGxG (for G infinite, KG ⊗ KG is a proper subset of KGxG). The set KG becomes a Hopf algebra if we define
- Δ : KG → KGxG by Δ(f)(x,y) = f(xy) for all f in KG and all x,y in G
- ε : KG → K by ε(f) = f(e) for every f in KG [here e is the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of G] - S : KG → KG by S(f)(x) = f(x−1) for all f in KG and all x in G.
- The Hopf algebra KG is always commutative; it is co-commutative if and only if the group is commutative.
- Note that functions on a finite group can be identified with the group ring, though these are more naturally thought of as dual – the group ring consists of finite sums of elements, and thus pairs with functions on the group by evaluating the function on the summed elements.
- Regular functions on an algebraic group. Generalizing the previous example, we can use the same formulas to show that for a given algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G over K, the set of all regular functionRegular functionIn mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
s on G forms a Hopf algebra. - Universal enveloping algebra. Suppose g is a Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
over the field K and U is its universal enveloping algebraUniversal enveloping algebraIn mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
. U becomes a Hopf algebra if we define- Δ : U → U ⊗ U by Δ(x) = x ⊗ 1 + 1 ⊗ x for every x in g (this rule is compatible with commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
s and can therefore be uniquely extended to all of U). - ε : U → K by ε(x) = 0 for all x in g (again, extended to U)
- S : U → U by S(x) = -x for all x in g.
- Δ : U → U ⊗ U by Δ(x) = x ⊗ 1 + 1 ⊗ x for every x in g (this rule is compatible with commutator
Cohomology of Lie groups
The cohomology algebra of a Lie group is a Hopf algebra: the multiplication is provided by the cup-product, and the comultiplication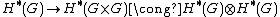
by the group multiplication
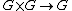 .
.This observation was actually a source of the notion of Hopf algebra. Using this structure, Hopf proved a structure theorem for the cohomology algebra of Lie groups.
Theorem (Hopf) Let A be a finite-dimensional, graded commutative, graded
cocommutative Hopf algebra over a field of characteristic 0. Then A (as an algebra) is a free exterior algebra with generators of odd degree.
Quantum groups and non-commutative geometry
All examples above are either commutative (i.e. the multiplication is commutative) or co-commutative (i.e. Δ = T Δ where T: H ⊗ H → H ⊗ H is defined by T(x ⊗ y) = y ⊗ x). Other interesting Hopf algebras are certain "deformations" or "quantization
Δ where T: H ⊗ H → H ⊗ H is defined by T(x ⊗ y) = y ⊗ x). Other interesting Hopf algebras are certain "deformations" or "quantizationQuantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
s" of those from example 3 which are neither commutative nor co-commutative. These Hopf algebras are often called quantum groups, a term that is so far only loosely defined. They are important in noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
, the idea being the following: a standard algebraic group is well described by its standard Hopf algebra of regular functions; we can then think of the deformed version of this Hopf algebra as describing a certain "non-standard" or "quantized" algebraic group (which is not an algebraic group at all). While there does not seem to be a direct way to define or manipulate these non-standard objects, one can still work with their Hopf algebras, and indeed one identifies them with their Hopf algebras. Hence the name "quantum group".
Related concepts
GradedGraded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
Hopf algebras are often used in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
: they are the natural algebraic structure on the direct sum of all homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
or cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
groups of an H-space
H-space
In mathematics, an H-space is a topological space X together with a continuous map μ : X × X → X with an identity element e so that μ = μ = x for all x in X...
.
Locally compact quantum group
Locally compact quantum group
The locally compact quantum group is a relatively new C*-algebraic formalism for quantum groups, generalizing the Kac algebra, compact quantum group and Hopf algebra approaches. Earlier attempts of a unifying definition of quantum groups using e.g...
s generalize Hopf algebras and carry a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. The algebra of all continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is a locally compact quantum group.
Quasi-Hopf algebras are generalizations of Hopf algebras, where coassociativity only holds up to a twist.
Weak Hopf algebras, or quantum groupoids, are generalizations of Hopf algebras. Like
Hopf algebras, weak Hopf algebras form a self-dual class of algebras; i.e., if H is a (weak) Hopf algebra, so is
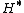 , the dual space of linear forms on H (with respect to the algebra-coalgebra structure obtained from the natural pairing with H and its coalgebra-algebra structure).
, the dual space of linear forms on H (with respect to the algebra-coalgebra structure obtained from the natural pairing with H and its coalgebra-algebra structure).A weak Hopf algebra H is usually taken to be a 1) finite dimensional algebra and coalgebra with coproduct
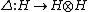 and counit
and counit 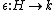
satisfying all the axioms of Hopf algebra except possibly
 or
or 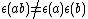
for some a,b in H. Instead one requires that
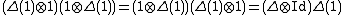 and
and 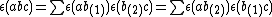
for all a,b, and c in H.
2) H has a weakened antipode
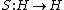 satisfying the axioms (a) - (c): (a)
satisfying the axioms (a) - (c): (a) 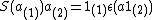 for all a in H (the right-hand side is the interesting
for all a in H (the right-hand side is the interestingprojection usually denoted by
 or
or 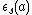
with image a separable subalgebra denoted by
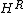 or
or  ); (b)
); (b) 
for all a in H (another interesting projection usually denoted by
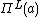 or
or 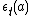
with image a separable algebra
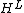 or
or 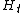 , anti-isomorphic to
, anti-isomorphic to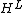 via S); and (c)
via S); and (c) 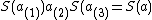
for all a in H. Note that if
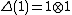 , these conditions reduce to the two usual conditions on the antipode of a Hopf algebra.
, these conditions reduce to the two usual conditions on the antipode of a Hopf algebra.The axioms are partly chosen so that the category of H-modules is a rigid tensor category.
The unit H-module is the separable algebra
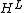 mentioned above.
mentioned above.For example, a finite groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
algebra is a weak Hopf algebra. In particular, the groupoid
algebra on [n] with one pair of invertible arrows
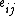 and
and  between i and j in [n] is isomorphic to the algebra H of n x n matrices. The weak Hopf algebra structure on this particular H is given by coproduct
between i and j in [n] is isomorphic to the algebra H of n x n matrices. The weak Hopf algebra structure on this particular H is given by coproduct 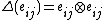 , counit
, counit  and antipode
and antipode 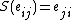 .
.The separable subalgebras
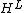 and
and 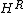 coincide and are non-central commutative algebras in this particular case (the subalgebra of diagonal matrices).
coincide and are non-central commutative algebras in this particular case (the subalgebra of diagonal matrices). Early theoretical contributions to weak Hopf algebras are to be found in as well as
Hopf algebroids introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry (later shown equivalent in nontrivial way to a construction of Takeuchi from the 1970s and another by Xu around the year 2000): Hopf algebroids generalize weak Hopf algebras and certain skew Hopf algebras. They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras
become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely
a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra
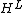 .
.The antipode axioms have been changed by G. Böhm and K. Szlachanyi (J. Algebra) in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
extensions.
A left Hopf algebroid (H,R) is a left bialgebroid together with an antipode: the bialgebroid (H,R)
consists of a total algebra H and a base algebra R and two mappings, an algebra
homomorphism
 called a source map, an algebra anti-homomorphism
called a source map, an algebra anti-homomorphism  called a target map, such that the commutativity condition
called a target map, such that the commutativity condition  is satisfied for all
is satisfied for all 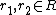 . The axioms resemble those of a Hopf algebra but are complicated by the possibility that R is a noncommutative algebra or its images under s and t are not in the center of H. In particular a left bialgebroid (H,R) has an R-R-bimodule structure on H which prefers the left side as follows:
. The axioms resemble those of a Hopf algebra but are complicated by the possibility that R is a noncommutative algebra or its images under s and t are not in the center of H. In particular a left bialgebroid (H,R) has an R-R-bimodule structure on H which prefers the left side as follows: 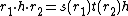 for all h in H,
for all h in H, 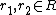 . There is a coproduct
. There is a coproduct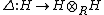 and counit
and counit 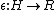
that make
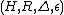 an R-coring (with axioms like that of a coalgebra
an R-coring (with axioms like that of a coalgebraCoalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
such that all mappings are R-R-bimodule homomorphisms and all tensors over R). Additionally the bialgebroid (H,R) must satisfy
 for all a,b in H, and a condition to make sure this last condition makes sense: every image point
for all a,b in H, and a condition to make sure this last condition makes sense: every image point 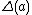 satisfies
satisfies 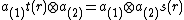 for all r in R. Also
for all r in R. Also 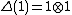 . The counit is required to satisfy
. The counit is required to satisfy 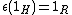 and the condition
and the condition 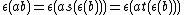 .
.The antipode
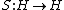 is usually taken to be an algebra anti-automorphism satisfying conditions of exchanging the source and target maps and satisfying two axioms like Hopf algebra antipode axioms; see the references in Lu or in Böhm-Szlachanyi for a more example-category friendly, though somewhat more complicated, set of axioms for the antipode S.
is usually taken to be an algebra anti-automorphism satisfying conditions of exchanging the source and target maps and satisfying two axioms like Hopf algebra antipode axioms; see the references in Lu or in Böhm-Szlachanyi for a more example-category friendly, though somewhat more complicated, set of axioms for the antipode S.The latter set of axioms depend on the axioms of a right bialgebroid as well, which are a straightforward switching of left to right, s with t, of the axioms for a left bialgebroid given above.
As an example of left bialgebroid, take R to be any algebra over a field k. Let H be its algebra of linear self-mappings. Let s(r) be left multication by r on R; let t(r) be right multiplication by r on R. H is a left bialgebroid over R, which may be seen as follows.
From the fact that
 one may define a coproduct by
one may define a coproduct by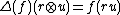 for each linear transformation f from R to itself
for each linear transformation f from R to itselfand all r,u in R. Coassociativity of the coproduct follows from associativity of the product on R. A counit is given by
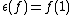 . The counit axioms of a coring follow from the identity element condition on multiplication in R. The reader will be amused, or at least edified, to check that (H,R) is a left bialgebroid. In case R is an Azumaya algebra, in which case
. The counit axioms of a coring follow from the identity element condition on multiplication in R. The reader will be amused, or at least edified, to check that (H,R) is a left bialgebroid. In case R is an Azumaya algebra, in which caseH is isomorphic to R tensor R, an antipode comes from transposing tensors, which makes H a Hopf algebroid over R.
Multiplier Hopf algebras introduced by Alfons Van Daele in 1994 are generalizations of Hopf algebras where comultiplication from an algebra (with or withthout unit) to the
multiplier algebra
Multiplier algebra
In C*-algebras, the multiplier algebra, denoted by M, of a C*-algebra A is a unital C*-algebra which is the largest unital C*-algebra that contains A as an ideal in a "non-degenerate" way. It is the noncommutative generalization of Stone–Čech compactification...
of tensor product algebra of the algebra with itself.
Hopf group-(co)algebras introduced by V.G.Turaev in 2000 are also generalizations of Hopf algebras.
Analogy with groups
Groups can be axiomatized by the same diagrams (equivalently, operations) as a Hopf algebra, where G is taken to be a set instead of a module. In this case:- the field K is replaced by the 1-point set
- there is a natural counit (map to 1 point)
- there is a natural comultiplication (the diagonal map)
- the unit is the identity element of the group
- the multiplication is the multiplication in the group
- the antipode is the inverse
In this philosophy, a group can be thought of as a Hopf algebra over the "field with one element
Field with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
".
See also
- Quasitriangular Hopf algebra
- Algebra/set analogy
- Representation theory of Hopf algebras
- Ribbon Hopf algebraRibbon Hopf algebraA ribbon Hopf algebra is a quasitriangular Hopf algebra which possess an invertible central element \nu more commonly known as the ribbon element, such that the following conditions hold:...
- SuperalgebraSuperalgebraIn mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
- SupergroupSupergroup (physics)The concept of supergroup is a generalization of that of group. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them....
- Anyonic Lie algebra
- Sweedler's Hopf algebraSweedler's Hopf algebraIn mathematics, introduced an example of an infinite-dimensional Hopf algebra, and Sweedler's Hopf algebra H4 is a certain 4-dimensional quotient of it that is neither commutative nor cocommutative.-Definition:...

