
Anticommutativity
Encyclopedia
In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operation
s are widely used in algebra
, geometry
, mathematical analysis
and, as a consequence, in physics
: they are often called antisymmetric operation
s.
 -ary operation is anticommutative if swapping the order of any two arguments negates the result. For example, a binary operation * is anti-commutative if for all x and y, x*y = −y*x.
-ary operation is anticommutative if swapping the order of any two arguments negates the result. For example, a binary operation * is anti-commutative if for all x and y, x*y = −y*x.
More formally, a map
 from the set of all n-tuples of elements in a set A (where n is a general integer) to a group
from the set of all n-tuples of elements in a set A (where n is a general integer) to a group
 is anticommutative if and only if
is anticommutative if and only if
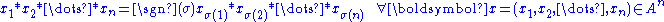
where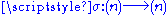 is an arbitrary permutation
is an arbitrary permutation
of the set (n) of the first n non-zero integers and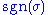 is its sign. This equality expresses the following concept:
is its sign. This equality expresses the following concept:
Note that this is an abuse of notation
, since the codomain
of the operation
needs only to be a group
: "−1" does not have a precise meaning since a multiplication
is not necessarily defined on .
.
Particularly important is the case n=2. A binary operation
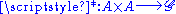 is anticommutative if and only if
is anticommutative if and only if
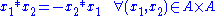
This means that is the inverse
is the inverse
of the element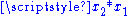 in
in  .
.
 is such that
is such that

i.e. the only element equal to its inverse
is the neutral element, then for all the ordered tuples such that for at least two different index
for at least two different index 
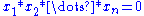
In the case this means
this means
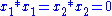
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
s are widely used in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and, as a consequence, in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
: they are often called antisymmetric operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
s.
Definition
An -ary operation is anticommutative if swapping the order of any two arguments negates the result. For example, a binary operation * is anti-commutative if for all x and y, x*y = −y*x.
-ary operation is anticommutative if swapping the order of any two arguments negates the result. For example, a binary operation * is anti-commutative if for all x and y, x*y = −y*x.More formally, a map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
 from the set of all n-tuples of elements in a set A (where n is a general integer) to a group
from the set of all n-tuples of elements in a set A (where n is a general integer) to a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
 is anticommutative if and only if
is anticommutative if and only ifIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
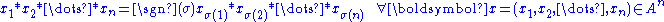
where
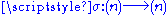 is an arbitrary permutation
is an arbitrary permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the set (n) of the first n non-zero integers and
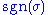 is its sign. This equality expresses the following concept:
is its sign. This equality expresses the following concept:
- the value of the operation is unchanged, when applied to all ordered tuples constructed by even permutationEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
of the elements of a fixed one. - the value of the operation is the inverse of its value on a fixed tuple, when applied to all ordered tuples constructed by odd permutationEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
to the elements of the fixed one. The need for the existence of this inverse element is the main reason for requiring the codomainCodomainIn mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
 of the operationOperation (mathematics)The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
of the operationOperation (mathematics)The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
to be at least a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
Note that this is an abuse of notation
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
, since the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
of the operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
needs only to be a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
: "−1" does not have a precise meaning since a multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
is not necessarily defined on
 .
.Particularly important is the case n=2. A binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
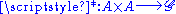 is anticommutative if and only if
is anticommutative if and only ifIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
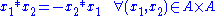
This means that
 is the inverse
is the inverseInverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
of the element
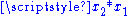 in
in  .
.Properties
If the group is such that
is such that
i.e. the only element equal to its inverse
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
is the neutral element, then for all the ordered tuples such that
 for at least two different index
for at least two different index 
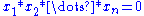
In the case
 this means
this means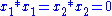
Examples
Anticommutative operators include:- SubtractionSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
- Cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
- Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
- Lie ringLie ringIn mathematics a Lie ring is a structure related to Lie algebras that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups.- Formal definition :...
See also
- CommutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
- CommutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
- Exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
- Operation (mathematics)Operation (mathematics)The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
- Symmetry in mathematicsSymmetry in mathematicsSymmetry occurs not only in geometry, but also in other branches of mathematics. It is actually the same as invariance: the property that something does not change under a set of transformations....
- Particle statisticsParticle statisticsParticle statistics refers to the particular description of particles in statistical mechanics.-Classical statistics:In classical mechanics all the particles in the system are considered distinguishable. This means that one can label and track each individual particle in a system...
(for anticommutativity in physics).

