Quantization (physics)
Encyclopedia
In physics
, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics
". It is a procedure for constructing a quantum field theory
starting from a classical field theory
. This is a generalization of the procedure for building quantum mechanics
from classical mechanics
. One also speaks of field quantization, as in the "quantization of the electromagnetic field
", where one refers to photons as field "quanta
" (for instance as light quanta). This procedure is basic to theories of particle physics
, nuclear physics
, condensed matter physics
, and quantum optics
.
s into operators acting on quantum states of the field theory. The lowest energy state is called the vacuum state
and may be very complicated. The reason for quantizing a theory is to deduce properties of materials, objects or particles through the computation of quantum amplitudes. Such computations have to deal with certain subtleties called renormalization
, which, if neglected, can often lead to nonsense results, such as the appearance of infinities in various amplitudes. The full specification of a quantization procedure requires methods of performing renormalization.
The first method to be developed for quantization of field theories was canonical quantization
. While this is extremely easy to implement on sufficiently simple theories, there are many situations where other methods of quantization yield more efficient procedures for computing quantum amplitudes. However, the use of canonical quantization
has left its mark on the language and interpretation of quantum field theory.
from classical mechanics
. The classical field
is treated as a dynamical variable called the canonical coordinate, and its time-derivative is the canonical momentum. One introduces a commutation relation between these which is exactly the same as the commutation relation between a particle's position and momentum in quantum mechanics
. Technically, one converts the field to an operator, through combinations of creation and annihilation operators
. The field operator acts on quantum states of the theory. The lowest energy state is called the vacuum state
. The procedure is also called second quantization.
This procedure can be applied to the quantization of any field
theory: whether of fermion
s or boson
s, and with any internal symmetry. However, it leads to a fairly simple picture of the vacuum state
and is not easily amenable to use in some quantum field theories
, such as quantum chromodynamics
which is known to have a complicated vacuum
characterized by many different condensates
.
. This method is based upon a classical action, but is different from the functional integral approach.
The method does not apply to all possible actions (like for instance actions with a noncausal structure or actions with gauge "flows"
). It starts with the classical algebra of all (smooth) functionals over the configuration space. This algebra is quotiented over by the ideal generated by the Euler–Lagrange equations. Then, this quotient algebra is converted into a Poisson algebra by introducing a Poisson bracket derivable from the action, called the Peierls bracket
. This Poisson algebra is then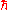
-deformed in the same way as in canonical quantization.
Actually, there is a way to quantize actions with gauge "flows"
. It involves the Batalin-Vilkovisky formalism
, an extension of the BRST formalism.
with the permissible configurations being the ones which are extremal with respect to functional variation
s of the action. A quantum-mechanical description of the classical system can also be constructed from the action of the system by means of the path integral formulation
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
". It is a procedure for constructing a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
starting from a classical field theory
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
. This is a generalization of the procedure for building quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
from classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. One also speaks of field quantization, as in the "quantization of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
", where one refers to photons as field "quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
" (for instance as light quanta). This procedure is basic to theories of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, nuclear physics
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
, condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, and quantum optics
Quantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
.
Quantization methods
Quantization converts classical fieldField (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
s into operators acting on quantum states of the field theory. The lowest energy state is called the vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
and may be very complicated. The reason for quantizing a theory is to deduce properties of materials, objects or particles through the computation of quantum amplitudes. Such computations have to deal with certain subtleties called renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, which, if neglected, can often lead to nonsense results, such as the appearance of infinities in various amplitudes. The full specification of a quantization procedure requires methods of performing renormalization.
The first method to be developed for quantization of field theories was canonical quantization
Canonical quantization
In physics, canonical quantization is a procedure for quantizing a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg's route to obtaining quantum mechanics...
. While this is extremely easy to implement on sufficiently simple theories, there are many situations where other methods of quantization yield more efficient procedures for computing quantum amplitudes. However, the use of canonical quantization
Canonical quantization
In physics, canonical quantization is a procedure for quantizing a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg's route to obtaining quantum mechanics...
has left its mark on the language and interpretation of quantum field theory.
Canonical quantization
Canonical quantization of a field theory is analogous to the construction of quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
from classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. The classical field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
is treated as a dynamical variable called the canonical coordinate, and its time-derivative is the canonical momentum. One introduces a commutation relation between these which is exactly the same as the commutation relation between a particle's position and momentum in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Technically, one converts the field to an operator, through combinations of creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
. The field operator acts on quantum states of the theory. The lowest energy state is called the vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
. The procedure is also called second quantization.
This procedure can be applied to the quantization of any field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
theory: whether of fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s or boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s, and with any internal symmetry. However, it leads to a fairly simple picture of the vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
and is not easily amenable to use in some quantum field theories
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, such as quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
which is known to have a complicated vacuum
QCD vacuum
The QCD vacuum is the vacuum state of quantum chromodynamics . It is an example of a non-perturbative vacuum state, characterized by many non-vanishing condensates such as the gluon condensate or the quark condensate...
characterized by many different condensates
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
.
Covariant canonical quantization
It turns out that there is a way to perform a canonical quantization without having to resort to the noncovariant approach of foliating spacetime and choosing a HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
. This method is based upon a classical action, but is different from the functional integral approach.
The method does not apply to all possible actions (like for instance actions with a noncausal structure or actions with gauge "flows"
Analysis of flows
In theoretical physics, an analysis of flows is the study of "gauge" or "gaugelike" "symmetries"...
). It starts with the classical algebra of all (smooth) functionals over the configuration space. This algebra is quotiented over by the ideal generated by the Euler–Lagrange equations. Then, this quotient algebra is converted into a Poisson algebra by introducing a Poisson bracket derivable from the action, called the Peierls bracket
Peierls bracket
In theoretical physics, the Peierls bracket is an equivalent description of the Poisson bracket. It directly follows from the action and does not require the canonical coordinates and their canonical momenta to be defined in advance.The bracket[A,B]...
. This Poisson algebra is then
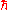-deformed in the same way as in canonical quantization.Actually, there is a way to quantize actions with gauge "flows"
Analysis of flows
In theoretical physics, an analysis of flows is the study of "gauge" or "gaugelike" "symmetries"...
. It involves the Batalin-Vilkovisky formalism
Batalin-Vilkovisky formalism
In theoretical physics, the Batalin–Vilkovisky formalism was developed as a method for determining the ghost structure for Lagrangian gauge theories, such as gravity and supergravity, whose corresponding Hamiltonian formulation has constraints not related to a Lie algebra In theoretical...
, an extension of the BRST formalism.
Deformation Quantization
See- Weyl quantizationWeyl quantizationIn mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
- Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
- Star productMoyal productIn mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
- Quantum characteristicsMethod of quantum characteristicsIn quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta...
Path integral quantization
A classical mechanical theory is given by an actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
with the permissible configurations being the ones which are extremal with respect to functional variation
Variation
- Physics :* Magnetic variation, difference between magnetic north and true north, measured as an angle* Variation , any perturbation of the mean motion or orbit of a planet or satellite, particularly of the moon- Mathematics :* Bounded variation...
s of the action. A quantum-mechanical description of the classical system can also be constructed from the action of the system by means of the path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
.
See also
- Feynman path integral
- Photon polarizationPhoton polarizationPhoton polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
- quantum Hall effect
- quantum numberQuantum numberQuantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...