
Bivector
Encyclopedia
In mathematics
, a bivector or 2-vector is a quantity in geometric algebra
or exterior algebra
that generalises the idea of a vector. If a scalar
is considered a zero dimension
al quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors have applications in many areas of mathematics and physics. They are related to complex number
s in two dimensions and to both pseudovector
s and quaternion
s in three dimensions. They can be used to generate rotations
in any dimension, and are a useful tool for classifying such rotations. They also are used in physics
, tying together a number of otherwise unrelated quantities.
Bivectors are generated by the exterior product
on vectors – given two vectors a and b their exterior product is a bivector. But not all bivectors can be generated this way, and in higher dimensions a sum of exterior products is often needed. More precisely a bivector that requires only a single exterior product is simple; in two and three dimensions all bivectors are simple, but in higher dimensions this is not generally the case. The exterior product is antisymmetric
, so is the negation of the bivector , producing a rotation with the opposite sense, and is the zero bivector.
Geometrically, a simple bivector can be interpreted as an oriented plane segment, much as vectors can be thought of as directed line segment
s. Specifically for the bivector , its magnitude
is the area of the parallelogram
with edges a and b, its attitude that of any plane specified by a and b, and its orientation the sense of the rotation that would align a with b. It does not have a definite location or position.
in exterior algebra
, as the result of the exterior product. Around the same time in 1843 in Ireland William Rowan Hamilton
discovered quaternions. It was not until English mathematician William Kingdon Clifford
in 1888 added the geometric product to Grassmann's algebra, incorporating the ideas of both Hamilton and Grassmann, and founded Clifford algebra
, that the bivector as it is known today was fully understood.
Around this time Josiah Willard Gibbs
and Oliver Heaviside
developed vector calculus which included separate cross product
and dot product
s, derived from quaternion multiplication. The success of vector calculus, and of the book Vector Analysis by Gibbs and Wilson
, meant the insights of Hamilton and Clifford were overlooked for a long time, as much of 20th century mathematics and physics was formulated in vector terms. Gibbs instead described bivectors as vectors, and used "bivector" to describe an unrelated quantity, a use that has sometimes been copied.
Today the bivector is largely studied as a topic in geometric algebra
, a more restricted Clifford algebra over real
or complex
vector space
s with nondegenerate
quadratic form
. Its resurgence was led by David Hestenes
who, along with others, discovered a range of new applications in physics
for geometric algebra.
with signature 1.
Associativity
:
Left and right distributivity
:
Contraction:
Where Q is the quadratic form, |a| is the magnitude
of a and ϵa is the signature
of the vector. For a space with Euclidean metric ϵa is 1 so can be omitted, and the contraction condition becomes:
is a sum of scalars and so a scalar. From the law of cosines
on the triangle formed by the vectors its value is |a||b|cosθ, where θ is the angle between the vectors. It is therefore identical to the interior product between two vectors, and is written the same way,
It is symmetric, scalar valued, and can be used to determine the angle between two vectors: in particular if a and b are orthogonal the product is zero.
This is called the exterior product, . It is antisymmetric
in a and b, that is
By addition:
That is the geometric product is the sum of the symmetric interior product and antisymmetric exterior product.
To calculate consider the sum
Expanding using the geometric product and simplifying gives
so using the Pythagorean trigonometric identity
:
With a negative square it cannot be a scalar or vector quantity, so it is a new sort of object, a bivector. It has magnitude
|a||b|sinθ, where θ is the angle between the vectors, and so is zero for parallel vectors.
To distinguish them from vectors, bivectors are written here with bold capitals, for example:

although other conventions are used, in particular as vectors and bivectors are both elements of the geometric algebra.
over the vector space. For a Euclidean vector space it is written or Cℓn(ℝ), where n is the dimension of the vector space ℝn. Cℓn is both a vector space and an algebra, generated by all the products between vectors in ℝn, so it contains all vectors and bivectors. More precisely as a vector space it contains the vectors and bivectors as subspace
or Cℓn(ℝ), where n is the dimension of the vector space ℝn. Cℓn is both a vector space and an algebra, generated by all the products between vectors in ℝn, so it contains all vectors and bivectors. More precisely as a vector space it contains the vectors and bivectors as subspace
s. The space of all bivectors is written Λ2ℝn. Unlike ℝn it is not a Euclidean subspace
; nor is it a subalgebra
.
). In two and three dimensions the even subalgebra contains only scalars and bivectors, and each is of particular interest. In two dimensions the even subalgebra is isomorphic to the complex number
s, ℂ, while in three it is isomorphic to the quaternion
s, ℍ. More generally the even subalgebra can be used to generate rotation
s in any dimension, and can be generated by bivectors in the algebra.
For general bivectors the magnitude can be calculated by taking the norm of the bivector considered as a vector in the space Λ2ℝn. If the magnitude is zero then all the bivector's components are zero, and the bivector is the zero bivector which as an element of the geometric algebra equals the scalar zero.
Of particular interest are the unit bivectors formed from the products of the Standard basis
. If ei and ej are distinct basis vectors then the product is a bivector. As the vectors are orthogonal this is just eiej, written eij, with unit magnitude as the vectors are unit vectors. The set of all such bivectors form a basis for Λ2ℝn. For instance in four dimensions the basis for Λ2ℝ4 is (e1e2, e1e3, e1e4, e2e3, e2e4, e3e4) or (e12, e13, e14, e23, e24, e34).
cannot be written as the exterior product of two vectors. A vector that can be written as the exterior product of two vectors is simple. In two and three dimensions all bivectors are simple, but not in four or more dimensions; in four dimensions every bivector is the sum of at most two exterior products. A bivector has a real square if and only if it is simple, and only simple bivectors can be represented geometrically by a oriented plane area.
The quantity is the scalar valued interior product, while is the grade 4 exterior product that arises in four or more dimensions. The quantity is the bivector valued commutator
product, given by
The space of bivectors Λ2ℝn are a Lie algebra
over ℝ, with the commutator product as the Lie bracket. The full geometric product of bivectors generates the even subalgebra.
Of particular interest is the product of a bivector with itself. As the commutator product is antisymmetric the product simplifies to
If the bivector is simple the last term is zero and the product is the scalar valued , which can be used as a check for simplicity. In particular the exterior product of bivectors only exists in four or more dimensions, so all bivectors in two and three dimensions are simple.
A vector in real two dimensional space ℝ2 can be written , where a1 and a2 are real numbers, e1 and e2 are orthonormal basis vectors. The geometric product of two such vectors is
This can be split into the symmetric, scalar valued, interior product and an antisymmetric, bivector valued exterior product:
All bivectors in two dimensions are of this form, that is multiples of the bivector e1e2, written e12 to emphasise it is a bivector rather than a vector. The magnitude of e12 is 1, with

so it is called the unit bivector. The term unit bivector can be used in other dimensions but it is only uniquely defined in two dimensions and all bivectors are multiples of e12. As the highest grade element of the algebra e12 is also the pseudoscalar which is given the symbol i.
from complex numbers. The bivectors and scalars together form the even subalgebra of the geometric algebra, which is isomorphic to the complex numbers ℂ. The even subalgebra has basis (1, e12), the whole algebra has basis (1, e1, e2, e12).
The complex numbers are usually identified with the coordinate axes
and two dimensional vectors, which would mean associating them with the vector elements of the geometric algebra. There is no contradiction in this, as to get from a general vector to a complex number an axis needs to be identified as the real axis, e1 say. This multiplies by all vectors to generate the elements of even subalgebra.
All the properties of complex numbers can be derived from bivectors, but two are of particular interest. First as with complex numbers products of bivectors and so the even subalgebra are commutative. This is only true in two dimensions, so properties of the bivector in two dimensions that depend on commutativity do not usually generalise to higher dimensions.
Second a general bivector can be written
where θ is a real number. Putting this into the Taylor series
for the exponential map
and using the property e122 = −1 results in a bivector version of Euler's formula
,
which when multiplied by any vector rotates it through an angle θ about the origin:
The product of a vector with a bivector in two dimensions is anticommutative, so the following products all generate the same rotation
Of these the last product is the one that generalises into higher dimensions. The quantity needed is called a rotor
and is given the symbol R, so in two dimensions a rotor that rotates through angle θ can be written
and the rotation it generates is
This can be split into the symmetric, scalar valued, interior product and the antisymmetric, bivector valued, exterior product:
In three dimensions all bivectors are simple and so the result of an exterior product. The unit bivectors e23, e31 and e12 form a basis for the space of bivectors Λ2ℝ3, which itself a three dimensional linear space. So if a general bivector is:
they can be added like vectors
while when multiplied they produce the following
which can be split into symmetric scalar and antisymmetric bivector parts as follows
The exterior product of two bivectors in three dimensions is zero.
A bivector B can be written as the product of its magnitude and a unit bivector, so writing β for |B| and using the Taylor series for the exponential map it can be shown that
This is another version of Euler's formula, but with a general bivector in three dimensions. Unlike in two dimensions bivectors are not commutative so properties that depend on commutativity do not apply in three dimensions. For example in general in three (or more) dimensions.
The full geometric algebra in three dimensions, Cℓ3(ℝ), has basis (1, e1, e2, e3, e23, e31, e12, e123). The element e123 is a trivector and the pseudoscalar
for the geometry. Bivectors in three dimensions are sometimes identified with pseudovector
s to which they are related, as discussed below.
The even subalgebra, that is the algebra consisting of scalars and bivectors, is isomorphic to the quaternion
s, ℍ. This can be seen by comparing the basis to the quaternion basis, or from the above product which is identical to the quaternion product, except for a change of sign which relates to the negative products in the bivector interior product . Other quaternion properties can be similarly related to or derived from geometric algebra.
This suggests that the usual split of a quaternion into scalar and vector parts would be better represented as a split into scalar and bivector parts; if this is done there is no special quaternion product, there is just the normal geometric product on the elements. It also relates quaternions in three dimensions to complex numbers in two, as each is isomorphic to the even subalgebra for the dimension, a relationship that generalises to higher dimensions.
representation of rotations, is a compact way of representing rotations in three dimensions. In its most compact form it consists of a vector, the product of the a unit vector that is the axis of rotation and the angle
of rotation, so the magnitude of the vector is the rotation angle.
In geometric algebra this vector is classified as a bivector. This can be seen in its relation to quaternions. If the axis is ω and the angle of rotation
is θ then the rotation vector is ωθ quaternion associated with the rotation is

but this is just the exponent of half of the bivector Ωθ, that is

So rotation vectors are bivectors, just as quaternions are elements of the geometric algebra, and they are related by the exponential map in that algebra.
As to two dimensions the quantity eΩθ is called a rotor
and written R. The quantity e -Ωθ is then R -1, and they generate rotations as follows
This is identical to two dimensions, except here rotors are four-dimensional objects isomorphic to the quaternions. This can be generalised to all dimensions, with rotors, elements of the even subalgebra with unit magnitude, being generated by the exponential map from bivectors. They form a double cover over the rotation group, so the rotors R and −R represent the same rotation.
; the general bivector maps to the matrix
This multiplied by vectors on both sides gives the same vector as the product of a vector and bivector; an example is the angular velocity tensor.
Skew symmetric matrices generate orthogonal matrices
with determinant
1 through the exponential map. In particular the exponent of a bivector associated with a rotation is a rotation matrix, that is the rotation matrix MR given by the above skew-symmetric matrix is

The rotation described by MR is the same as that described by the rotor R given by
and the matrix MR can be also calculated directly from rotor R:
Bivectors are related to the eigenvalues of a rotation matrix. Given a rotation matrix M the eigenvalues can calculated by solving the characteristic equation
for that matrix . By the fundamental theorem of algebra
this has three roots, but only one real root as there is only one eigenvector, the axis of rotation. The other roots must be a complex conjugate pair. They have unit magnitude so purely imaginary logarithms, equal to the magnitude of the bivector associated with the rotation, which is also the angle of rotation. The eigenvectors associated with the complex eigenvalues are in the plane of the bivector, so the exterior product of two non-parallel eigenvectors result in the bivector, or at least a multiple of it.
, angular momentum
and vector magnetic field
s. Such quantities can be described as bivectors in geometric algebra; that is quantities that might use axial vectors in vector algebra
are better represented by bivectors in geometric algebra. More precisely, the Hodge dual gives the isomorphism between axial vectors and bivectors, so each axial vector is associated with a bivector and vice-versa; that is
where * indicates the Hodge dual. Alternately, using the unit pseudoscalar in Cℓ3(ℝ), i = e1e2e3 gives
This is easier to use as the product is just the geometric product. But it is antisymmetric because (as in two dimensions) the unit pseudoscalar i squares to −1, so a negative is needed in one of the products.
This relationship extends to operations like the vector valued cross product
and bivector valued exterior product, as when written as determinant
s they are calculated in the same way:
so are related by the Hodge dual:

Bivectors have a number of advantages over axial vectors. They better disambiguate axial and polar vectors, that is the quantities represented by them, so it is clearer which operations are allowed and what their results are. For example the inner product of a polar vector and an axial vector resulting from the cross product in the triple product
should result in a pseudoscalar
, a result which is more obvious if the calculation is framed as the exterior product of a vector and bivector. They generalises to other dimensions; in particular bivectors can be used to describe quantities like torque and angular momentum in two as well as three dimensions. Also, they closely match geometric intuition in a number of ways, as seen in the next section.
All bivectors can be interpreted as planes, or more precisely as directed plane segments. In three dimensions there are three properties of a bivector that can be interpreted geometrically:
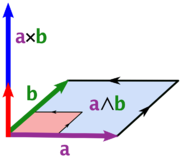 In three dimensions all bivectors can be generated by the exterior product of two vectors. If the bivector then the magnitude of B is
In three dimensions all bivectors can be generated by the exterior product of two vectors. If the bivector then the magnitude of B is
where θ is the angle between the vectors. This is the area of the parallelogram
with edges a and b, as shown in the diagram. One interpretation is that the area is swept out by b as it moves along a. The exterior product is antisymmetric, so reversing the order of a and b to make a move along b results in a bivector with the opposite direction that is the negative of the first. The plane of bivector a ∧ b contains both a and b so they are both parallel to the plane.
Bivectors and axial vectors are related by Hodge dual. In a real vector space the Hodge dual relates a subspace to its orthogonal complement, so if a bivector is represented by a plane then the axial vector associated with it is simply the plane's surface normal
. The plane has two normals, one on each side, giving the two possible orientation
s for the plane and bivector.
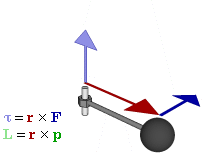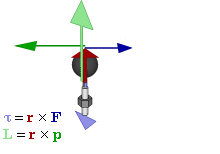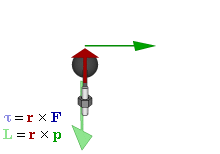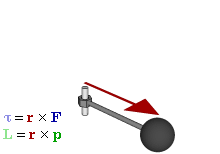 This relates the cross product
This relates the cross product
to the exterior product. It can also be used to represent physical quantities, like torque
and angular momentum
. In vector algebra they are usually represented by vectors, perpendicular to the plane of the force
, linear momentum or displacement that they are calculated from. But if a bivector is used instead the plane is the plane of the bivector, so is a more natural way to represent the quantities and the way they act. It also unlike the vector representation generalises into other dimensions.
The product of two bivectors has a geometric interpretation. For non-zero bivectors A and B the product can be split into symmetric and antisymmetric parts as follows:
Like vectors these have magnitudes and , where θ is the angle between the planes. In three dimensions it is the same as the angle between the normal vectors dual to the planes, and it generalises to some extent in higher dimensions.
Bivectors can be added together as areas. Given two non-zero bivectors B and C in three dimensions it is always possible to find a vector that is contained in both, a say, so the bivectors can be written as exterior products involving a:
This can be interpreted geometrically as seen in the diagram: the two areas sum to give a third, with the three areas forming faces of a prism
with a, b, c and as edges. This corresponds to the two ways of calculating the area using the distributivity
of the exterior product:
This only works in three dimensions as it is the only dimension where a vector parallel to both bivectors must exist. In higher dimensions bivectors generally are not associated with a single plane, or if they are (simple bivectors) two bivectors may have no vector in common, and so sum to a non-simple bivector.
The element e1234 is the pseudoscalar in Cℓ4, distinct from the scalar, so the square is non-scalar.
All bivectors in four dimensions can be generated using at most two exterior products and four vectors. The above bivector can be written as
Alternately every bivector can be written as the sum of two simple bivectors. It is useful to choose two orthogonal bivectors for this, and this is always possible to do. Moreover for a general bivector the choice of simple bivectors is unique, that is there is only one way to decompose into orthogonal bivectors. This is true also for simple bivectors, except one of the orthogonal parts is zero. The exception is when the two orthogonal bivectors have equal magnitudes (as in the above example): in this case the decomposition is not unique.
 The rotations generated are more complex though. They can be categorised as follows:
The rotations generated are more complex though. They can be categorised as follows:
These are generated by bivectors in a straightforward way. Simple rotations are generated by simple bivectors, with the fixed plane the dual or orthogonal to the plane of the bivector. The rotation can be said to take place about that plane, in the plane of the bivector. All other bivectors generate double rotations, with the two angles of the rotation equalling the magnitudes of the two simple bivectors the non-simple bivector is composed of. Isoclinic rotations arise when these magnitudes are equal, in which case the decomposition into two simple bivectors in not unique.
Bivectors in general do not commute, but one exception is orthogonal bivectors and exponents of them. So if the bivector , where B1 and B2 are orthogonal simple bivectors, is used to generate a rotation it decomposes into two simple rotations that commute as follows:
It is always possible to do this as all bivectors can be expressed as sums of orthogonal bivectors.
is a mathematical model for our universe used in special relativity. It consists of three space
dimensions and one time
dimension combined into a single four dimensional space. It is naturally described if using geometric algebra and bivectors, with the Euclidean metric replaced by a Minkowski metric. That is the algebra is identical to that of Euclidean space, except the signature
is changed, so
(Note the order and indices above are not universal – here e4 is the time-like dimension). The geometric algebra is Cℓ3,1(ℝ), and the subspace of bivectors is Λ2ℝ3,1. The bivectors are of two types. The bivectors e23, e31 and e12 have negative squares and correspond to the bivectors of the three dimensional subspace corresponding to Euclidean space, ℝ3. These bivectors generate normal rotations in ℝ3.
The bivectors e14, e24 and e34 have positive squares and as planes span a space dimension and the time dimension. These also generate rotations through the exponential map, but instead of trigonometric functions hyperbolic functions are needed, which generates a rotor as follows:
These are Lorentz transformation
s, expressed in a particularly compact way, using the same algebra as in ℝ3 and ℝ4. In general all spacetime rotations are generated from bivectors through the exponential map, that is, a general rotor generated by bivector A is of the form
The set of all rotations in spacetime form the Lorentz group
, and from them most of the consequences of special relativity can be deduced. More generally this show how transformations in Euclidean space and spacetime can all be described using the same algebra.
Maxwell's equations
are used in physics to describe the relationship between electric
and magnetic
fields. Normally given as four differential equations they have a particularly compact form when the fields are expressed as a spacetime bivector from Λ2ℝ3,1. If the electric and magnetic fields in ℝ3 are and then the electromagnetic bivector is
where e4 is again the basis vector for the time-like dimension and c is the speed of light
. The quantity e123 is the bivector dual to in three dimensions, as discussed above, while e4 as a product of orthogonal vectors is also bivector valued. As a whole it is the electromagnetic tensor
expressed more compactly as a bivector, and is used as follows. First it is related to the 4-current J, a vector quantity given by
where is current density
and ρ is charge density
. They are related by a differential operator ∂, which is
The operator ∇ is a differential operator
in geometric algebra, acting on the space dimensions and given by . When applied to vectors ∇·M is the divergence
and ∇∧M is the curl but with a bivector rather than vector result, that is dual in three dimensions to the curl. For general quantity M they act as grade lowering and raising differential operators. In particular if M is a scalar then this operator is just the gradient
, and it can be thought of as a geometric algebraic del
operator.
Together these can be used to give a particularly compact form for Maxwell's equations in a vacuum:
This when decomposed according to geometric algebra, using geometric products which have both grade raising and grade lowering effects, is equivalent to Maxwell's four equations. This is the form in a vacuum, but the general form is only a little more complex. It is also related to the electromagnetic four-potential
, a vector A given by
where is the vector magnetic potential and V is the electric potential. It is related to the electromagnetic bivector as follows
using the same differential operator ∂.
The number of simple bivectors needed to form a general bivector rises with the dimension, so for n odd it is (n - 1) / 2, for n even it is n / 2. So for four and five dimensions only two simple bivectors are needed but three are required for six and seven
dimensions. For example in six dimensions with standard basis (e1, e2, e3, e4, e5, e6) the bivector
is the sum of three simple bivectors but no less. As in four dimensions it is always possible to find orthogonal simple bivectors for this sum.
is the rotor generated by bivector B. Simple rotations, that take place in a plane of rotation
around a fixed blade of dimension (n - 2) are generated by with simple bivectors, while other bivectors generate more complex rotations which can be described in terms of the simple bivectors they are sums of, each related to a plane of rotation. All bivectors can be expressed as the sum of orthogonal and commutative simple bivectors, so rotations can always be decomposed into a set of commutative rotations about the planes associated with these bivectors. The group of the rotors in n dimensions is the spin group, Spin(n).
One notable feature, related to the number of simple bivectors and so rotation planes, is that in odd dimensions every rotation has a fixed axis - it is misleading to call it an axis of rotation as in higher dimensions rotations are taking place in multiple planes orthogonal to it. This is related to bivectors, as bivectors in odd dimensions decompose into the same number of bivectors as the even dimension below, so have the same number of planes, but one extra dimension. As each plane generates rotations in two dimensions in odd dimensions there must be one dimension, that is an axis, that is not being rotated.
Bivectors are also related to the rotation matrix in n dimensions. As in three dimensions the characteristic equation
of the matrix can be solved to find the eigenvalues. In odd dimensions this has one real root, with eigenvector the fixed axis, and in even dimensions it has no real roots, so either all or all but one of the roots are complex conjugate pairs. Each pair is associated with a simple component of the bivector associated with the rotation. In particular the log of each pair is ± the magnitude, while eigenvectors generated from the roots are parallel to and so can be used to generate the bivector. In general the eigenvalues and bivectors are unique, and the set of eigenvalues gives the full decomposition into simple bivectors; if roots are repeated then the decomposition of the bivector into simple bivectors is not unique.
in a straightforward way. The geometric algebra used is , the algebra of the real vector space ℝn. This is used to describe objects in the real projective space
ℝℙn - 1. The non-zero vectors in Cℓn(ℝ) or ℝn are associated with points in the projective space so vectors that differ only by a scale factor, so their exterior product is zero, map to the same point. Non-zero simple bivectors in Λ2ℝn represent lines in ℝℙn - 1, with bivectors differing only by a (positive or negative) scale factor representing the same line.
A description of the projective geometry can be constructed in the geometric algebra using basic operations. For example given two distinct points in ℝℙn - 1 represented by vectors a and b the line between them is given by (or ). Two lines intersect in a point if for their bivectors A and B. This point is given by the vector
The operation "⋁" is the meet, which can be defined as above in terms of the join, for non-zero . Using these operations projective geometry can be formulated in terms of geometric algebra. For example given a third (non-zero) bivector C the point p lies on the line given by C if and only if
So the condition for the lines given by A, B and C to be collinear is
which in Cℓ3(ℝ) and ℝℙ2 simplifies to
where the angle brackets denote the scalar part of the geometric product. In the same way all projective space operations can be written in terms of geometric algebra, with bivectors representing general lines in projective space, so the whole geometry can be developed using geometric algebra.
, respectively a 3x3 and 4x4 skew-symmetric matrix or tensor.
Real bivectors in Λ2ℝn are isomorphic to n×n skew-symmetric matrices, or alternately to antisymmetric tensor
s of order 2 on ℝn. While bivectors are isomorphic to vectors (via the dual) in three dimensions they can be represented by skew-symmetric matrices in any dimension. This is useful for relating bivectors to problems described by matrices, so they can be re-cast in terms of bivectors, given a geometric interpretation, then often solved more easily or related geometrically to other bivector problems.
More generally every real geometric algebra is isomorphic to a matrix algebra. These contain bivectors as a subspace, though often in a way which is not especially useful. These matrices are mainly of interest as a way of classifying Clifford algebras.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bivector or 2-vector is a quantity in geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
or exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
that generalises the idea of a vector. If a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
is considered a zero dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors have applications in many areas of mathematics and physics. They are related to complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s in two dimensions and to both pseudovector
Pseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
s and quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s in three dimensions. They can be used to generate rotations
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
in any dimension, and are a useful tool for classifying such rotations. They also are used in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, tying together a number of otherwise unrelated quantities.
Bivectors are generated by the exterior product
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
on vectors – given two vectors a and b their exterior product is a bivector. But not all bivectors can be generated this way, and in higher dimensions a sum of exterior products is often needed. More precisely a bivector that requires only a single exterior product is simple; in two and three dimensions all bivectors are simple, but in higher dimensions this is not generally the case. The exterior product is antisymmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
, so is the negation of the bivector , producing a rotation with the opposite sense, and is the zero bivector.
Geometrically, a simple bivector can be interpreted as an oriented plane segment, much as vectors can be thought of as directed line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s. Specifically for the bivector , its magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
is the area of the parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
with edges a and b, its attitude that of any plane specified by a and b, and its orientation the sense of the rotation that would align a with b. It does not have a definite location or position.
History
The bivector was first defined in 1844 by German mathematician Hermann GrassmannHermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
in exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
, as the result of the exterior product. Around the same time in 1843 in Ireland William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
discovered quaternions. It was not until English mathematician William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
in 1888 added the geometric product to Grassmann's algebra, incorporating the ideas of both Hamilton and Grassmann, and founded Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
, that the bivector as it is known today was fully understood.
Around this time Josiah Willard Gibbs
Josiah Willard Gibbs
Josiah Willard Gibbs was an American theoretical physicist, chemist, and mathematician. He devised much of the theoretical foundation for chemical thermodynamics as well as physical chemistry. As a mathematician, he invented vector analysis . Yale University awarded Gibbs the first American Ph.D...
and Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
developed vector calculus which included separate cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s, derived from quaternion multiplication. The success of vector calculus, and of the book Vector Analysis by Gibbs and Wilson
Edwin Bidwell Wilson
Edwin Bidwell Wilson was an American mathematician and polymath. He was the sole protégé of Yale's physicist Josiah Willard Gibbs and was mentor to MIT economist Paul Samuelson. He received his AB from Harvard College in 1899 and his PhD from Yale University in 1901, working under Gibbs.E.B...
, meant the insights of Hamilton and Clifford were overlooked for a long time, as much of 20th century mathematics and physics was formulated in vector terms. Gibbs instead described bivectors as vectors, and used "bivector" to describe an unrelated quantity, a use that has sometimes been copied.
Today the bivector is largely studied as a topic in geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, a more restricted Clifford algebra over real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s with nondegenerate
Degeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
. Its resurgence was led by David Hestenes
David Hestenes
David Orlin Hestenes, Ph.D. is a physicist. For more than 30 years, he was employed in the Department of Physics and Astronomy of Arizona State University , where he retired with the rank of Research Professor and is now emeritus....
who, along with others, discovered a range of new applications in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
for geometric algebra.
Formal definition
For this article the bivector will be considered only in real geometric algebras. This in practice is not much of a restriction, as all useful applications are drawn from such algebras. Also unless otherwise stated, all examples have a Euclidean metric and so a quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
with signature 1.
Geometric algebra and the geometric product
The bivector arises from the definition of the geometric product over a vector space. For vectors a, b and c, the geometric product on vectors is defined as follows:Associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
:
Left and right distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
:
Contraction:
Where Q is the quadratic form, |a| is the magnitude
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of a and ϵa is the signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
of the vector. For a space with Euclidean metric ϵa is 1 so can be omitted, and the contraction condition becomes:
The interior product
From associativity , a scalar times b. So ab cannot be a scalar. Butis a sum of scalars and so a scalar. From the law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
on the triangle formed by the vectors its value is |a||b|cosθ, where θ is the angle between the vectors. It is therefore identical to the interior product between two vectors, and is written the same way,
It is symmetric, scalar valued, and can be used to determine the angle between two vectors: in particular if a and b are orthogonal the product is zero.
The exterior product
In the same way another quantity can be written down:This is called the exterior product, . It is antisymmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
in a and b, that is
By addition:
That is the geometric product is the sum of the symmetric interior product and antisymmetric exterior product.
To calculate consider the sum
Expanding using the geometric product and simplifying gives
so using the Pythagorean trigonometric identity
Pythagorean trigonometric identity
The Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one the basic relations between the sine and cosine functions, from which all others may be derived.-Statement of...
:
With a negative square it cannot be a scalar or vector quantity, so it is a new sort of object, a bivector. It has magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
|a||b|sinθ, where θ is the angle between the vectors, and so is zero for parallel vectors.
To distinguish them from vectors, bivectors are written here with bold capitals, for example:

although other conventions are used, in particular as vectors and bivectors are both elements of the geometric algebra.
The space Λ2ℝn
The algebra generated by the geometric product is the geometric algebraGeometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
over the vector space. For a Euclidean vector space it is written
 or Cℓn(ℝ), where n is the dimension of the vector space ℝn. Cℓn is both a vector space and an algebra, generated by all the products between vectors in ℝn, so it contains all vectors and bivectors. More precisely as a vector space it contains the vectors and bivectors as subspace
or Cℓn(ℝ), where n is the dimension of the vector space ℝn. Cℓn is both a vector space and an algebra, generated by all the products between vectors in ℝn, so it contains all vectors and bivectors. More precisely as a vector space it contains the vectors and bivectors as subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
s. The space of all bivectors is written Λ2ℝn. Unlike ℝn it is not a Euclidean subspace
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
; nor is it a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
.
The even subalgebra
The subalgebra generated by the bivectors is the even subalgebra of the geometric algebra, written . This algebra results from considering all products of scalars and bivectors generated by the geometric product. It has dimension 2n - 1, and contains Λ2ℝn as a linear subspace with dimension n(n - 1) (a triangular numberTriangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
). In two and three dimensions the even subalgebra contains only scalars and bivectors, and each is of particular interest. In two dimensions the even subalgebra is isomorphic to the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, ℂ, while in three it is isomorphic to the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, ℍ. More generally the even subalgebra can be used to generate rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
s in any dimension, and can be generated by bivectors in the algebra.
Magnitude
As noted in the previous section the magnitude of a simple bivector, that is one that is the exterior product of two vectors a and b, is |a||b|sin θ, where θ is the angle between the vectors. It is written |B|, where B is the bivector.For general bivectors the magnitude can be calculated by taking the norm of the bivector considered as a vector in the space Λ2ℝn. If the magnitude is zero then all the bivector's components are zero, and the bivector is the zero bivector which as an element of the geometric algebra equals the scalar zero.
Unit bivectors
A unit bivector is one with unit magnitude. It can be derived from any non-zero bivector by dividing the bivector by its magnitude, that isOf particular interest are the unit bivectors formed from the products of the Standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
. If ei and ej are distinct basis vectors then the product is a bivector. As the vectors are orthogonal this is just eiej, written eij, with unit magnitude as the vectors are unit vectors. The set of all such bivectors form a basis for Λ2ℝn. For instance in four dimensions the basis for Λ2ℝ4 is (e1e2, e1e3, e1e4, e2e3, e2e4, e3e4) or (e12, e13, e14, e23, e24, e34).
Simple bivectors
The exterior product of two vectors is a bivector, but not all bivectors are exterior products of two vectors. For example in four dimensions the bivectorcannot be written as the exterior product of two vectors. A vector that can be written as the exterior product of two vectors is simple. In two and three dimensions all bivectors are simple, but not in four or more dimensions; in four dimensions every bivector is the sum of at most two exterior products. A bivector has a real square if and only if it is simple, and only simple bivectors can be represented geometrically by a oriented plane area.
Product of two bivectors
The geometric product of two bivectors, A and B, isThe quantity is the scalar valued interior product, while is the grade 4 exterior product that arises in four or more dimensions. The quantity is the bivector valued commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
product, given by
The space of bivectors Λ2ℝn are a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
over ℝ, with the commutator product as the Lie bracket. The full geometric product of bivectors generates the even subalgebra.
Of particular interest is the product of a bivector with itself. As the commutator product is antisymmetric the product simplifies to
If the bivector is simple the last term is zero and the product is the scalar valued , which can be used as a check for simplicity. In particular the exterior product of bivectors only exists in four or more dimensions, so all bivectors in two and three dimensions are simple.
Two dimensions
When working with coordinates in geometric algebra it is usual to write the basis vectors as (e1, e2, ...), a convention that will be used here.A vector in real two dimensional space ℝ2 can be written , where a1 and a2 are real numbers, e1 and e2 are orthonormal basis vectors. The geometric product of two such vectors is
This can be split into the symmetric, scalar valued, interior product and an antisymmetric, bivector valued exterior product:
All bivectors in two dimensions are of this form, that is multiples of the bivector e1e2, written e12 to emphasise it is a bivector rather than a vector. The magnitude of e12 is 1, with

so it is called the unit bivector. The term unit bivector can be used in other dimensions but it is only uniquely defined in two dimensions and all bivectors are multiples of e12. As the highest grade element of the algebra e12 is also the pseudoscalar which is given the symbol i.
Complex numbers
With the properties of negative square and unit magnitude the unit bivector can be identified with the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
from complex numbers. The bivectors and scalars together form the even subalgebra of the geometric algebra, which is isomorphic to the complex numbers ℂ. The even subalgebra has basis (1, e12), the whole algebra has basis (1, e1, e2, e12).
The complex numbers are usually identified with the coordinate axes
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
and two dimensional vectors, which would mean associating them with the vector elements of the geometric algebra. There is no contradiction in this, as to get from a general vector to a complex number an axis needs to be identified as the real axis, e1 say. This multiplies by all vectors to generate the elements of even subalgebra.
All the properties of complex numbers can be derived from bivectors, but two are of particular interest. First as with complex numbers products of bivectors and so the even subalgebra are commutative. This is only true in two dimensions, so properties of the bivector in two dimensions that depend on commutativity do not usually generalise to higher dimensions.
Second a general bivector can be written
where θ is a real number. Putting this into the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
and using the property e122 = −1 results in a bivector version of Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
,
which when multiplied by any vector rotates it through an angle θ about the origin:
The product of a vector with a bivector in two dimensions is anticommutative, so the following products all generate the same rotation
Of these the last product is the one that generalises into higher dimensions. The quantity needed is called a rotor
Rotor (mathematics)
A rotor is an n-blade object in geometric algebra, which rotates another n-blade object about a fixed or translated point. They are normally motivated by considering an even number of reflections, which generate rotations...
and is given the symbol R, so in two dimensions a rotor that rotates through angle θ can be written
and the rotation it generates is
Three dimensions
In three dimensions the geometric product of two vectors isThis can be split into the symmetric, scalar valued, interior product and the antisymmetric, bivector valued, exterior product:
In three dimensions all bivectors are simple and so the result of an exterior product. The unit bivectors e23, e31 and e12 form a basis for the space of bivectors Λ2ℝ3, which itself a three dimensional linear space. So if a general bivector is:
they can be added like vectors
while when multiplied they produce the following
which can be split into symmetric scalar and antisymmetric bivector parts as follows
The exterior product of two bivectors in three dimensions is zero.
A bivector B can be written as the product of its magnitude and a unit bivector, so writing β for |B| and using the Taylor series for the exponential map it can be shown that
This is another version of Euler's formula, but with a general bivector in three dimensions. Unlike in two dimensions bivectors are not commutative so properties that depend on commutativity do not apply in three dimensions. For example in general in three (or more) dimensions.
The full geometric algebra in three dimensions, Cℓ3(ℝ), has basis (1, e1, e2, e3, e23, e31, e12, e123). The element e123 is a trivector and the pseudoscalar
Pseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
for the geometry. Bivectors in three dimensions are sometimes identified with pseudovector
Pseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
s to which they are related, as discussed below.
Quaternions
Bivectors are not closed under the geometric product, but the even subalgebra is. In three dimensions it consists of all scalar and bivector elements of the geometric algebra, so a general element can be written for example a + A, where a is the scalar part and A is the bivector part. It is written and has basis (1, e23, e31, e12). The product of two general elements of the even subalgebra isThe even subalgebra, that is the algebra consisting of scalars and bivectors, is isomorphic to the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, ℍ. This can be seen by comparing the basis to the quaternion basis, or from the above product which is identical to the quaternion product, except for a change of sign which relates to the negative products in the bivector interior product . Other quaternion properties can be similarly related to or derived from geometric algebra.
This suggests that the usual split of a quaternion into scalar and vector parts would be better represented as a split into scalar and bivector parts; if this is done there is no special quaternion product, there is just the normal geometric product on the elements. It also relates quaternions in three dimensions to complex numbers in two, as each is isomorphic to the even subalgebra for the dimension, a relationship that generalises to higher dimensions.
Rotation vector
The rotation vector, from the axis angleAxis angle
The axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation by two values: a unit vector indicating the direction of a directed axis , and an angle describing the magnitude of the rotation about the axis...
representation of rotations, is a compact way of representing rotations in three dimensions. In its most compact form it consists of a vector, the product of the a unit vector that is the axis of rotation and the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
of rotation, so the magnitude of the vector is the rotation angle.
In geometric algebra this vector is classified as a bivector. This can be seen in its relation to quaternions. If the axis is ω and the angle of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
is θ then the rotation vector is ωθ quaternion associated with the rotation is

but this is just the exponent of half of the bivector Ωθ, that is

So rotation vectors are bivectors, just as quaternions are elements of the geometric algebra, and they are related by the exponential map in that algebra.
Rotors
The bivector Ωθ generates a rotation through the exponential map. The even elements generated rotate a general vector in three dimensions in the same way as quaternions:As to two dimensions the quantity eΩθ is called a rotor
Rotor (mathematics)
A rotor is an n-blade object in geometric algebra, which rotates another n-blade object about a fixed or translated point. They are normally motivated by considering an even number of reflections, which generate rotations...
and written R. The quantity e -Ωθ is then R -1, and they generate rotations as follows
This is identical to two dimensions, except here rotors are four-dimensional objects isomorphic to the quaternions. This can be generalised to all dimensions, with rotors, elements of the even subalgebra with unit magnitude, being generated by the exponential map from bivectors. They form a double cover over the rotation group, so the rotors R and −R represent the same rotation.
Matrices
Bivectors are isomorphic to skew-symmetric matricesSkew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
; the general bivector maps to the matrix
This multiplied by vectors on both sides gives the same vector as the product of a vector and bivector; an example is the angular velocity tensor.
Skew symmetric matrices generate orthogonal matrices
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1 through the exponential map. In particular the exponent of a bivector associated with a rotation is a rotation matrix, that is the rotation matrix MR given by the above skew-symmetric matrix is

The rotation described by MR is the same as that described by the rotor R given by
and the matrix MR can be also calculated directly from rotor R:
Bivectors are related to the eigenvalues of a rotation matrix. Given a rotation matrix M the eigenvalues can calculated by solving the characteristic equation
Characteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...
for that matrix . By the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
this has three roots, but only one real root as there is only one eigenvector, the axis of rotation. The other roots must be a complex conjugate pair. They have unit magnitude so purely imaginary logarithms, equal to the magnitude of the bivector associated with the rotation, which is also the angle of rotation. The eigenvectors associated with the complex eigenvalues are in the plane of the bivector, so the exterior product of two non-parallel eigenvectors result in the bivector, or at least a multiple of it.
Axial vectors
The rotation vector is an example of an axial vector. Axial vectors or pseudovectors are vectors that undergo a sign change compared to normal or polar vectors under inversion, that is when reflected or otherwise inverted. Examples include quantities like torqueTorque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
, angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
and vector magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s. Such quantities can be described as bivectors in geometric algebra; that is quantities that might use axial vectors in vector algebra
Vector algebra
In mathematics, vector algebra may mean:* Linear algebra, specifically the basic algebraic operations of vector addition and scalar multiplication; see vector space....
are better represented by bivectors in geometric algebra. More precisely, the Hodge dual gives the isomorphism between axial vectors and bivectors, so each axial vector is associated with a bivector and vice-versa; that is
where * indicates the Hodge dual. Alternately, using the unit pseudoscalar in Cℓ3(ℝ), i = e1e2e3 gives
This is easier to use as the product is just the geometric product. But it is antisymmetric because (as in two dimensions) the unit pseudoscalar i squares to −1, so a negative is needed in one of the products.
This relationship extends to operations like the vector valued cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and bivector valued exterior product, as when written as determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s they are calculated in the same way:
so are related by the Hodge dual:

Bivectors have a number of advantages over axial vectors. They better disambiguate axial and polar vectors, that is the quantities represented by them, so it is clearer which operations are allowed and what their results are. For example the inner product of a polar vector and an axial vector resulting from the cross product in the triple product
Triple product
In mathematics, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product....
should result in a pseudoscalar
Pseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
, a result which is more obvious if the calculation is framed as the exterior product of a vector and bivector. They generalises to other dimensions; in particular bivectors can be used to describe quantities like torque and angular momentum in two as well as three dimensions. Also, they closely match geometric intuition in a number of ways, as seen in the next section.
Geometric interpretation
As suggested by their name and that of the algebra, one of the attractions of bivectors is that they have a natural geometric interpretation. This can be described in any dimension but is best done in three where parallels can be drawn with more familiar objects, before being applied to higher dimensions. In two dimensions the geometric interpretation is trivial, as the space is two dimensional so has only one plane, and all bivectors are associated with it differing only by a scale factor.All bivectors can be interpreted as planes, or more precisely as directed plane segments. In three dimensions there are three properties of a bivector that can be interpreted geometrically:
- The arrangement of the plane in space, precisely the attitude of the plane (or alternately the rotationRotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
, geometric orientationOrientation (geometry)In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
or gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the plane), is associated with the ratio of the bivector components. In particular the three basis bivectors, e23, e31 and e12, or scalar multiples of them, are associated with the yz-plane, xz-plane and xy-plane respectively. - The magnitudeMagnitude (mathematics)The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of the bivector is associated with the areaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of the plane segment. The area does not have a particular shape so any shape can be used. It can even be represented in other ways, such as by an angular measure. But if the vectors are interpreted as lengths the bivector is usually interpreted as an area with the same units, as follows. - Like the direction of a vector a plane associated with a bivector has a direction, a circulation or a sense of rotation in the plane, which takes two values seen as clockwise and counterclockwise when viewed from viewpoint not in the plane. This is associated with a change of sign in the bivector, that is if the direction is reversed the bivector is negated. Alternately if two bivectors have the same attitude and magnitude but opposite directions then one is the negative of the other.

where θ is the angle between the vectors. This is the area of the parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
with edges a and b, as shown in the diagram. One interpretation is that the area is swept out by b as it moves along a. The exterior product is antisymmetric, so reversing the order of a and b to make a move along b results in a bivector with the opposite direction that is the negative of the first. The plane of bivector a ∧ b contains both a and b so they are both parallel to the plane.
Bivectors and axial vectors are related by Hodge dual. In a real vector space the Hodge dual relates a subspace to its orthogonal complement, so if a bivector is represented by a plane then the axial vector associated with it is simply the plane's surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
. The plane has two normals, one on each side, giving the two possible orientation
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
s for the plane and bivector.

Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
to the exterior product. It can also be used to represent physical quantities, like torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. In vector algebra they are usually represented by vectors, perpendicular to the plane of the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, linear momentum or displacement that they are calculated from. But if a bivector is used instead the plane is the plane of the bivector, so is a more natural way to represent the quantities and the way they act. It also unlike the vector representation generalises into other dimensions.
The product of two bivectors has a geometric interpretation. For non-zero bivectors A and B the product can be split into symmetric and antisymmetric parts as follows:
Like vectors these have magnitudes and , where θ is the angle between the planes. In three dimensions it is the same as the angle between the normal vectors dual to the planes, and it generalises to some extent in higher dimensions.
Bivectors can be added together as areas. Given two non-zero bivectors B and C in three dimensions it is always possible to find a vector that is contained in both, a say, so the bivectors can be written as exterior products involving a:
This can be interpreted geometrically as seen in the diagram: the two areas sum to give a third, with the three areas forming faces of a prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
with a, b, c and as edges. This corresponds to the two ways of calculating the area using the distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
of the exterior product:
This only works in three dimensions as it is the only dimension where a vector parallel to both bivectors must exist. In higher dimensions bivectors generally are not associated with a single plane, or if they are (simple bivectors) two bivectors may have no vector in common, and so sum to a non-simple bivector.
Four dimensions
In four dimensions the basis elements for the space Λ2ℝ4 of bivectors are (e12, e13, e14, e23, e24, e34), so a general bivector is of the formOrthogonality
In four dimensions bivectors are orthogonal to bivectors. That is the dual of a bivector is a bivector, and the space Λ2ℝ4 is dual to itself in Cℓ4(ℝ). Normal vectors are not unique, instead every plane is orthogonal to all the vectors in its dual space. This can be used to partition the bivectors into two 'halves', for example into two sets of three unit bivectors each. There are only four distinct ways to do this, and whenever it's done one vector is in only one of the two halves, for example (e12, e13, e14) and (e23, e24, e34).Simple bivectors in 4D
In four dimensions bivectors are generated by the exterior product of vectors in ℝ4, but with one important difference from ℝ3 and ℝ2. In four dimensions not all bivectors are simple. There are bivectors such as that cannot be generated by the external product of two vectors. This also means they do not have a real, that is scalar, square. In this caseThe element e1234 is the pseudoscalar in Cℓ4, distinct from the scalar, so the square is non-scalar.
All bivectors in four dimensions can be generated using at most two exterior products and four vectors. The above bivector can be written as
Alternately every bivector can be written as the sum of two simple bivectors. It is useful to choose two orthogonal bivectors for this, and this is always possible to do. Moreover for a general bivector the choice of simple bivectors is unique, that is there is only one way to decompose into orthogonal bivectors. This is true also for simple bivectors, except one of the orthogonal parts is zero. The exception is when the two orthogonal bivectors have equal magnitudes (as in the above example): in this case the decomposition is not unique.
Rotations in ℝ4
As in three dimensions bivectors in four dimension generate rotations through the exponential map, and all rotations can be generated this way. As in three dimensions if B is a bivector then the rotor R is eB/2 and rotations are generated in the same way:
- simple rotations are those that fix a plane in 4D, and rotate by an angle "about" this plane.
- double rotations have only one fixed point, the origin, and rotate through two angles about two orthogonal planes. In general the angles are different and the planes are uniquely specified
- isoclinic rotations are double rotations where the angles of rotation are equal. In this case the planes about which the rotation is taking place are not unique.
These are generated by bivectors in a straightforward way. Simple rotations are generated by simple bivectors, with the fixed plane the dual or orthogonal to the plane of the bivector. The rotation can be said to take place about that plane, in the plane of the bivector. All other bivectors generate double rotations, with the two angles of the rotation equalling the magnitudes of the two simple bivectors the non-simple bivector is composed of. Isoclinic rotations arise when these magnitudes are equal, in which case the decomposition into two simple bivectors in not unique.
Bivectors in general do not commute, but one exception is orthogonal bivectors and exponents of them. So if the bivector , where B1 and B2 are orthogonal simple bivectors, is used to generate a rotation it decomposes into two simple rotations that commute as follows:
It is always possible to do this as all bivectors can be expressed as sums of orthogonal bivectors.
Spacetime rotations
SpacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is a mathematical model for our universe used in special relativity. It consists of three space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
dimensions and one time
Time in physics
Time in physics is defined by its measurement: time is what a clock reads. It is a scalar quantity and, like length, mass, and charge, is usually described as a fundamental quantity. Time can be combined mathematically with other physical quantities to derive other concepts such as motion, kinetic...
dimension combined into a single four dimensional space. It is naturally described if using geometric algebra and bivectors, with the Euclidean metric replaced by a Minkowski metric. That is the algebra is identical to that of Euclidean space, except the signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
is changed, so
(Note the order and indices above are not universal – here e4 is the time-like dimension). The geometric algebra is Cℓ3,1(ℝ), and the subspace of bivectors is Λ2ℝ3,1. The bivectors are of two types. The bivectors e23, e31 and e12 have negative squares and correspond to the bivectors of the three dimensional subspace corresponding to Euclidean space, ℝ3. These bivectors generate normal rotations in ℝ3.
The bivectors e14, e24 and e34 have positive squares and as planes span a space dimension and the time dimension. These also generate rotations through the exponential map, but instead of trigonometric functions hyperbolic functions are needed, which generates a rotor as follows:
These are Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s, expressed in a particularly compact way, using the same algebra as in ℝ3 and ℝ4. In general all spacetime rotations are generated from bivectors through the exponential map, that is, a general rotor generated by bivector A is of the form
The set of all rotations in spacetime form the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, and from them most of the consequences of special relativity can be deduced. More generally this show how transformations in Euclidean space and spacetime can all be described using the same algebra.
Maxwell's equations
(Note: in this section traditional 3-vectors are indicated by lines over the symbols and spacetime vector and bivectors by bold symbols, with the vectors J and A exceptionally in uppercase)Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
are used in physics to describe the relationship between electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
fields. Normally given as four differential equations they have a particularly compact form when the fields are expressed as a spacetime bivector from Λ2ℝ3,1. If the electric and magnetic fields in ℝ3 are and then the electromagnetic bivector is
where e4 is again the basis vector for the time-like dimension and c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. The quantity e123 is the bivector dual to in three dimensions, as discussed above, while e4 as a product of orthogonal vectors is also bivector valued. As a whole it is the electromagnetic tensor
Electromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
expressed more compactly as a bivector, and is used as follows. First it is related to the 4-current J, a vector quantity given by
where is current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
and ρ is charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
. They are related by a differential operator ∂, which is
The operator ∇ is a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
in geometric algebra, acting on the space dimensions and given by . When applied to vectors ∇·M is the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
and ∇∧M is the curl but with a bivector rather than vector result, that is dual in three dimensions to the curl. For general quantity M they act as grade lowering and raising differential operators. In particular if M is a scalar then this operator is just the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, and it can be thought of as a geometric algebraic del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
operator.
Together these can be used to give a particularly compact form for Maxwell's equations in a vacuum:
This when decomposed according to geometric algebra, using geometric products which have both grade raising and grade lowering effects, is equivalent to Maxwell's four equations. This is the form in a vacuum, but the general form is only a little more complex. It is also related to the electromagnetic four-potential
Electromagnetic four-potential
The electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
, a vector A given by
where is the vector magnetic potential and V is the electric potential. It is related to the electromagnetic bivector as follows
using the same differential operator ∂.
Higher dimensions
As has been suggested in earlier sections much of geometric algebra generalises well into higher dimensions. The geometric algebra for the real space ℝn is Cℓn(ℝ), and the subspace of bivectors is Λ2ℝn.The number of simple bivectors needed to form a general bivector rises with the dimension, so for n odd it is (n - 1) / 2, for n even it is n / 2. So for four and five dimensions only two simple bivectors are needed but three are required for six and seven
Seven-dimensional space
In physics and mathematics, a sequence of n numbers can also be understood as a location in n-dimensional space. When n = 7, the set of all such locations is called 7-dimensional Euclidean space...
dimensions. For example in six dimensions with standard basis (e1, e2, e3, e4, e5, e6) the bivector
is the sum of three simple bivectors but no less. As in four dimensions it is always possible to find orthogonal simple bivectors for this sum.
Rotations in higher dimensions
As in three and four dimensions rotors are generated by the exponential map, sois the rotor generated by bivector B. Simple rotations, that take place in a plane of rotation
Plane of rotation
In geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
around a fixed blade of dimension (n - 2) are generated by with simple bivectors, while other bivectors generate more complex rotations which can be described in terms of the simple bivectors they are sums of, each related to a plane of rotation. All bivectors can be expressed as the sum of orthogonal and commutative simple bivectors, so rotations can always be decomposed into a set of commutative rotations about the planes associated with these bivectors. The group of the rotors in n dimensions is the spin group, Spin(n).
One notable feature, related to the number of simple bivectors and so rotation planes, is that in odd dimensions every rotation has a fixed axis - it is misleading to call it an axis of rotation as in higher dimensions rotations are taking place in multiple planes orthogonal to it. This is related to bivectors, as bivectors in odd dimensions decompose into the same number of bivectors as the even dimension below, so have the same number of planes, but one extra dimension. As each plane generates rotations in two dimensions in odd dimensions there must be one dimension, that is an axis, that is not being rotated.
Bivectors are also related to the rotation matrix in n dimensions. As in three dimensions the characteristic equation
Characteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...
of the matrix can be solved to find the eigenvalues. In odd dimensions this has one real root, with eigenvector the fixed axis, and in even dimensions it has no real roots, so either all or all but one of the roots are complex conjugate pairs. Each pair is associated with a simple component of the bivector associated with the rotation. In particular the log of each pair is ± the magnitude, while eigenvectors generated from the roots are parallel to and so can be used to generate the bivector. In general the eigenvalues and bivectors are unique, and the set of eigenvalues gives the full decomposition into simple bivectors; if roots are repeated then the decomposition of the bivector into simple bivectors is not unique.
Projective geometry
Geometric algebra can be applied to projective geometryProjective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
in a straightforward way. The geometric algebra used is , the algebra of the real vector space ℝn. This is used to describe objects in the real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
ℝℙn - 1. The non-zero vectors in Cℓn(ℝ) or ℝn are associated with points in the projective space so vectors that differ only by a scale factor, so their exterior product is zero, map to the same point. Non-zero simple bivectors in Λ2ℝn represent lines in ℝℙn - 1, with bivectors differing only by a (positive or negative) scale factor representing the same line.
A description of the projective geometry can be constructed in the geometric algebra using basic operations. For example given two distinct points in ℝℙn - 1 represented by vectors a and b the line between them is given by (or ). Two lines intersect in a point if for their bivectors A and B. This point is given by the vector
The operation "⋁" is the meet, which can be defined as above in terms of the join, for non-zero . Using these operations projective geometry can be formulated in terms of geometric algebra. For example given a third (non-zero) bivector C the point p lies on the line given by C if and only if
So the condition for the lines given by A, B and C to be collinear is
which in Cℓ3(ℝ) and ℝℙ2 simplifies to
where the angle brackets denote the scalar part of the geometric product. In the same way all projective space operations can be written in terms of geometric algebra, with bivectors representing general lines in projective space, so the whole geometry can be developed using geometric algebra.
Tensors and matrices
As noted above a bivector can be written as a skew-symmetric matrix, which through the exponential map generates a rotation matrix that describes the same rotation as the rotor, also generated by the exponential map but applied to the vector. But it is also used with other bivectors such as the angular velocity tensor and the electromagnetic tensorElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
, respectively a 3x3 and 4x4 skew-symmetric matrix or tensor.
Real bivectors in Λ2ℝn are isomorphic to n×n skew-symmetric matrices, or alternately to antisymmetric tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s of order 2 on ℝn. While bivectors are isomorphic to vectors (via the dual) in three dimensions they can be represented by skew-symmetric matrices in any dimension. This is useful for relating bivectors to problems described by matrices, so they can be re-cast in terms of bivectors, given a geometric interpretation, then often solved more easily or related geometrically to other bivector problems.
More generally every real geometric algebra is isomorphic to a matrix algebra. These contain bivectors as a subspace, though often in a way which is not especially useful. These matrices are mainly of interest as a way of classifying Clifford algebras.



































































