
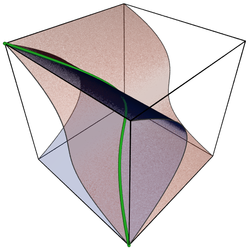
Algebraic variety
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic variety is the set of solutions of a system of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s. Algebraic varieties are one of the central objects of study in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. The word "variety" is employed in the sense of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, for which cognate
Cognate
In linguistics, cognates are words that have a common etymological origin. This learned term derives from the Latin cognatus . Cognates within the same language are called doublets. Strictly speaking, loanwords from another language are usually not meant by the term, e.g...
s of the word "variety" are used in the Romance languages.
Proven around the year 1800, the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
establishes a link between algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
by showing that a monic polynomial in one variable with complex coefficients (an algebraic object) is determined by the set of its roots (a geometric object). Building on this result, Hilbert's Nullstellensatz
Hilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
provides a fundamental correspondence between ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s and subsets of affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
. Using the Nullstellensatz and related results, mathematicians are able to capture the geometric notion of a variety
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
in algebraic terms as well as bring geometry to bear on questions of ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
.
Formal definitions
Algebraic varieties can be classed into four kinds: affine varieties, quasi-affine varieties, projective varieties, and quasi-projective varieties. There is also the more general notion of an abstract algebraic varietyAbstract algebraic variety
In algebraic geometry, an abstract algebraic variety is an algebraic variety that is defined intrinsically, that is, without an embedding into another variety....
.
Affine varieties
Let k be an algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
and let An be an affine n-space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
over k. The polynomials ƒ in the ring k[x1, ..., xn] can be viewed as k-valued functions on An by evaluating ƒ at the points in An. For each finitely generated ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
S in k[x1, ..., xn], define the zero-locus Z(S) to be the set of points in An on which the functions in S simultaneously vanish, that is to say
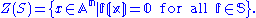
A subset V of An is called an affine algebraic set
Algebraic set
In mathematics, an algebraic set over an algebraically closed field K is the set of solutions in Kn of a set of simultaneous equationsand so on up to...
if V = Z(S) for some S. A nonempty affine algebraic set V is called irreducible if it cannot be written as the union of two proper
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
algebraic subsets. An irreducible affine algebraic set is also called an affine variety. (Many authors use the phrase affine variety to refer to any affine algebraic set, irreducible or not; this article will use the stricter definition.)
Affine varieties can be given a natural topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
by declaring the closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s to be precisely the affine algebraic sets. This topology is called the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
.
Given a subset V of An, we define I(V) to be the ideal of all functions vanishing on V:

For any affine algebraic set V, the coordinate ring or structure ring of V is the quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of the polynomial ring by this ideal.
Projective varieties
Let k be an algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
and let Pn be a projective n-space
Algebraic geometry of projective spaces
Projective spaces play a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of those spaces.- Homogeneous polynomial ideals:...
over k. Let f ∈ k [x0, ..., xn] be a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree d. It is not well-defined to evaluate f on points in Pn in homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. However, because f is homogeneous, f(λx0, ..., λxn) = λdf(x0, ..., xn), so it does make sense to ask whether f vanishes at a point [x0 : ... : xn]. For each set S of homogeneous polynomials, define the zero-locus of S to be the set of points in Pn on which the functions in S vanish:
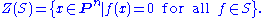
A subset V of Pn is called a projective algebraic set if V = Z(S) for some S. An irreducible projective algebraic set is called a projective variety.
Projective varieties are also equipped with the Zariski topology by declaring all algebraic sets to be closed.
Given a subset V of Pn, let I(V) be the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by all homogeneous polynomials vanishing on V. For any projective algebraic set V, the coordinate ring of V is the quotient of the polynomial ring by this ideal.
Example 1
Let k be the field of complex numbers C. Let A2 be a two dimensional affine space over C. The polynomials f in the ring k[x, y] can be viewed as complex valued functions on A2 by evaluating ƒ at the points in A2. Let subset S of k[x, y] contain a single element f(x, y):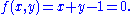
The zero-locus of f(x, y) is the set of points in A2 on which this function vanishes: it is the set of all pairs of complex numbers (x,y) such that y = 1 − x, commonly known as a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
. This is the set Z(f):
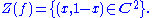
Thus the subset V = Z(f) of A2 is an algebraic set. The set V is not an empty set. And it is irreducible as it cannot be written as the union of two proper algebraic subsets. Thus it is an affine algebraic variety.
Example 2
Let again k be the field of complex numbers C. Let A2 be a two dimensional affine space over C. The polynomials g in the ring k[x, y] can be viewed as complex valued functions on A2 by evaluating g at the points in A2. Let subset S of k[x, y] contain a single element g(x, y):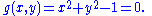
The zero-locus of g(x, y) is the set of points in A2 on which this function vanishes, that is the set of points (x,y) such that xx + yy = 1, commonly known as a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.
Basic results
- An affine algebraic set V is a variety if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
I(V) is a prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
; equivalently, V is a variety if and only if its coordinate ring is an integral domain. - Every nonempty affine algebraic set may be written uniquely as a union of algebraic varieties (where none of the sets in the decomposition are subsets of each other).
- Let k[V] be the coordinate ring of the variety V. Then the dimension of V is the transcendence degreeTranscendence degreeIn abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of the field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of k[V] over k.
Isomorphism of algebraic varieties
Let V1 and V2 be algebraic varieties. We say that V1 and V2 are isomorphicGraph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
, and write V1 ≅ V2, if there are regular map
Regular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
s φ : V1 → V2 and ψ : V2 → V1 such that the compositions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
ψ ° φ and φ ° ψ are the identity maps
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on V1 and V2 respectively.
Discussion and generalizations
The basic definitions and facts above enable one to do classical algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. To be able to do more — for example, to deal with varieties over fields that are not algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
— some foundational changes are required. The modern notion of a variety is considerably more abstract than the one above, though equivalent in the case of varieties over algebraically closed fields. An abstract algebraic variety is a particular kind of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
; the generalization to schemes on the geometric side enables an extension of the correspondence described above to a wider class of rings. A scheme is a locally ringed space such that every point has a neighbourhood, which, as a locally ringed space, is isomorphic to a spectrum of a ring
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
. Basically, a variety is a scheme whose structure sheaf is a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of k-algebras with the property that the rings R that occur above are all domains and are all finitely generated k-algebras, i.e., quotients of polynomial algebras by prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s.
This definition works over any field k. It allows you to glue affine varieties (along common open sets) without
worrying whether the resulting object can be put into some projective space. This also leads to difficulties since one can introduce somewhat pathological objects, e.g. an affine line with zero doubled. Such objects are usually not considered varieties, and are eliminated by requiring the schemes underlying a variety to be separated. (Strictly speaking, there is also a third condition, namely, that one needs only finitely many affine patches in the definition above.)
Some modern researchers also remove the restriction on a variety having integral domain affine charts, and when speaking of a variety simply mean that the affine charts have trivial nilradical.
A complete variety is a variety such that any map from an open subset of a nonsingular curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
into it can be extended uniquely to the whole curve. Every projective variety is complete, but not vice versa.
These varieties have been called 'varieties in the sense of Serre', since Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
's foundational paper FAC on sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
was written for them. They remain typical objects to start studying in algebraic geometry, even if more general objects are also used in an auxiliary way.
One way that leads to generalisations is to allow reducible algebraic sets (and fields k that aren't algebraically closed), so the rings R may not be integral domains. A more significant modification is to allow nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
s in the sheaf of rings. A nilpotent in a field must be 0: these if allowed in coordinate rings aren't seen as coordinate functions.
From the categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
point of view, nilpotents must be allowed, in order to have finite limits of varieties (to get fiber products). Geometrically this says that fibres of good mappings may have 'infinitesimal' structure. In the theory of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s of Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
these points are all reconciled: but the general scheme is far from having the immediate geometric content of a variety.
There are further generalizations called algebraic space
Algebraic space
In mathematics, an algebraic space is a generalization of the schemes of algebraic geometry introduced by Michael Artin for use in deformation theory...
s and stacks.
Algebraic manifolds
An algebraic manifold is an algebraic variety which is also an m-dimensional manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, and hence every sufficiently small local patch is isomorphic to km. Equivalently, the variety is smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
(free from singular points
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
). When k is the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, R, algebraic manifolds are called Nash manifolds. Algebraic manifolds can be defined as the zero set of a finite collection of analytic algebraic functions. Projective algebraic manifolds are an equivalent definition for projective varieties. The Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
is one example.
See also
- function field of an algebraic varietyFunction field of an algebraic varietyIn algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
- dimension of an algebraic varietyDimension of an algebraic varietyIn mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
- singular point of an algebraic varietySingular point of an algebraic varietyIn mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
- birational geometryBirational geometryIn mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
- abelian varietyAbelian varietyIn mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
- motiveMotive (algebraic geometry)In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
- schemeScheme (mathematics)In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
- analytic varietyAnalytic varietyIn mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...

