Multivector
Encyclopedia
In multilinear algebra
, a multivector or clif is an element of the (graded) exterior algebra
on a vector space
,
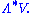This algebra consists of linear combination
s of simple k-vectors (also known as decomposable k-vectors or k-blades)
"Multivector" may mean either homogeneous elements (all terms of the sum have the same grade or degree k), which are referred to as k-vectors or p-vectors, or may allow sums of terms in different degrees, or may refer specifically to elements of mixed degree.
The k-th exterior power,
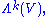
is the vector space of formal sums of k-multivectors. The product of a k-multivector and an
-multivector is a 
-multivector. So, the direct sum 
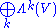forms an associative algebra, which is closed with respect to the wedge product. This algebra, commonly denoted by 
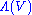, is called the exterior algebra
of V.
In differential geometry, a p-vector is the tensor
obtained by taking linear combination
s of the wedge product of p tangent vector
s, for some integer p ≥ 1. It is the dual
concept to a p-form.
For p = 2 and 3, these are often called respectively bivector
s and trivectors; they are dual to 2-forms and 3-forms.
In the presence of a volume form
(such as given an inner product and an orientation), pseudovectors and pseudoscalars can be identified with vectors and scalars, which is routine in vector calculus, but without a volume form this cannot be done without a choice.
In the Algebra of physical space
(the geometric algebra of Euclidean 3-space, used as a model of 3+1 spacetime), a sum of a scalar and a vector is called a paravector
, and represents a point in spacetime (the vector the space, the scalar the time).
tensor product
of a tangent space
with itself.
In geometric algebra
, also, a bivector is a grade 2 element (a 2-vector) resulting from the wedge product of two vectors, and so it is geometrically an oriented area, in the same way a vector is an oriented line segment.
If a and b are two vectors, the bivector a ∧ b has
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
, a multivector or clif is an element of the (graded) exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
,
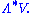This algebra consists of linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of simple k-vectors (also known as decomposable k-vectors or k-blades)
"Multivector" may mean either homogeneous elements (all terms of the sum have the same grade or degree k), which are referred to as k-vectors or p-vectors, or may allow sums of terms in different degrees, or may refer specifically to elements of mixed degree.
The k-th exterior power,
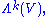
is the vector space of formal sums of k-multivectors. The product of a k-multivector and an
-multivector is a -multivector. So, the direct sum 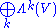forms an associative algebra, which is closed with respect to the wedge product. This algebra, commonly denoted by 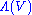, is called the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of V.
In differential geometry, a p-vector is the tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
obtained by taking linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of the wedge product of p tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s, for some integer p ≥ 1. It is the dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
concept to a p-form.
For p = 2 and 3, these are often called respectively bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s and trivectors; they are dual to 2-forms and 3-forms.
Examples
- 0-vectors are scalars;
- 1-vectors are vectors;
- 2-vectors are bivectorBivectorIn mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s; - (n-1)-vectors are pseudovectorPseudovectorIn physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
s; - n-vectors are pseudoscalarPseudoscalarIn physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
s.
In the presence of a volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
(such as given an inner product and an orientation), pseudovectors and pseudoscalars can be identified with vectors and scalars, which is routine in vector calculus, but without a volume form this cannot be done without a choice.
In the Algebra of physical space
Algebra of physical space
In physics, the algebra of physical space is the use of the Clifford or geometric algebra Cℓ3 of the three-dimensional Euclidean space as a model for -dimensional space-time, representing a point in space-time via a paravector .The Clifford algebra Cℓ3 has a faithful representation, generated by...
(the geometric algebra of Euclidean 3-space, used as a model of 3+1 spacetime), a sum of a scalar and a vector is called a paravector
Paravector
The name paravector is used for the sum of a scalar and a vector in any Clifford algebra This name was given by J. G...
, and represents a point in spacetime (the vector the space, the scalar the time).
Bivectors
A bivector is therefore an element of the antisymmetricAntisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of a tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
with itself.
In geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, also, a bivector is a grade 2 element (a 2-vector) resulting from the wedge product of two vectors, and so it is geometrically an oriented area, in the same way a vector is an oriented line segment.
If a and b are two vectors, the bivector a ∧ b has
- a normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
which is its area, given by
-
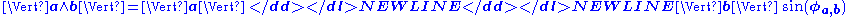
- a direction: the plane where that area lies on, i.e., the plane determined by a and b, as long as they are linearly independent;
- an orientation (out of two), determined by the order in which the originating vectors are multiplied.
Bivectors are connected to pseudovectorPseudovectorIn physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
s, and are used to represent rotations in geometric algebra.
As bivectors are elements of a vector space Λ2V (where V is a finite-dimensional vector space with
), it makes sense to define an inner product on this vector space as follows. First, write any element F ∈ Λ2V in terms of a basis as
where the Einstein summation convention is being used.
Now define a map by insisting that
-
where
are a set of numbers.
Geometric algebra
In geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, multivectors are defined to be summations of different-grade k-blades, such as the summation of a scalarScalar (mathematics)In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, a vector, and a 2-vector. A sum of only n-grade components is called an n-vector, or a homogeneous multivector.
The highest grade element in a space is called the pseudoscalarPseudoscalarIn physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
.
Applications
Bivectors play many important roles in physics, for example, in the classification of electromagnetic fieldsClassification of electromagnetic fieldsIn differential geometry and theoretical physics, the classification of electromagnetic fields is a pointwise classification of bivectors at each point of a Lorentzian manifold....
.
