In representation theory

Representation theory

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...

 of Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

s and Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

s, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group
or Lie algebra whose highest weight is a fundamental weight. For example, the defining module of a classical Lie group is a fundamental representation. Any finite-dimensional irreducible representation of a semisimple Lie group or Lie algebra can be constructed from the fundamental representations by a procedure due to Élie Cartan

Élie Cartan

Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...

. Thus in a certain sense, the fundamental representations are the elementary building blocks for arbitrary finite-dimensional representations.

Examples

• In the case of the general linear group
  General linear group
  In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
  
  , all fundamental representations are exterior powers of the defining module.
• In the case of the special unitary group SU(n), the n − 1 fundamental representations are the wedge products 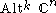consisting of the alternating tensors, for k = 1, 2, ..., n − 1.
• The spin representation of the twofold cover of an odd orthogonal group
  Orthogonal group
  In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
  
  , the odd spin group, and the two half-spin representations of the twofold cover of an even orthogonal group, the even spinor group, are fundamental representations that cannot be realized in the space of tensors.
• The adjoint representation
  Adjoint representation
  In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
  
   of the simple Lie group of type E₈
  E8 (mathematics)
  In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
  
   is a fundamental representation.

Explanation

The irreducible representations

Representation of a Lie group

In mathematics and theoretical physics, the idea of a representation of a Lie group plays an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie...

 of a simply-connected  compact

Compact group

In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...

 Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

 are indexed by their highest weights

Weight (representation theory)

In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...

. These weights are the lattice points in an orthant Q₊ in the weight lattice of the Lie group consisting of the dominant integral weights. It can be proved
that there exists a set of fundamental weights, indexed by the vertices of the Dynkin diagram, such that any dominant integral weight is a non-negative integer linear combinations of the fundamental weights. The corresponding irreducible representations are the fundamental representations of the Lie group. From the expansion of a dominant weight in terms of the fundamental weights one can take a corresponding tensor product of the fundamental representations and extract one copy of the irreducible representation corresponding to that dominant weight.

Other uses

Outside of Lie theory, the term fundamental representation is sometimes loosely used to refer to a smallest-dimensional faithful representation, though this is also often called the standard or defining representation (a term referring more to the history, rather than having a well-defined mathematical meaning).