Graded algebra
Encyclopedia
In mathematics
, in particular abstract algebra
, a graded algebra is an algebra over a field
(or commutative ring
) with an extra piece of structure, known as a gradation (or grading).
The grading is a direct sum decomposition of the algebra with factors indexed in a special way by a monoid
. Given a pair of elements from two factors of the grading, the indexing allows one to know which factor of the grading will contain the product of the chosen elements.
that has a direct sum decomposition into (abelian) additive groups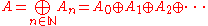
such that the ring multiplication satisfies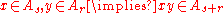
and so
Elements of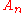
are known as homogeneous elements of degree n. An ideal
or other subset
⊂ A is homogeneous if for every element a ∈ 
, the homogeneous parts of a are also contained in 
If I is a homogeneous ideal in A, then
is also a graded ring, and has decomposition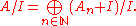
Any (non-graded) ring A can be given a gradation by letting A0 = A, and Ai = 0 for i > 0. This is called the trivial gradation on A.
M over a graded ring A such that also
and
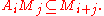
This idea is much used in commutative algebra
, and elsewhere, to define under mild hypotheses a Hilbert function, namely the length
of Mn as a function of n. Again under mild hypotheses of finiteness, this function is a polynomial, the Hilbert polynomial
, for all large enough values of n (see also Hilbert-Samuel polynomial).
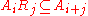
and
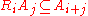
Note that the definition of the graded ring over a ring with no grading is the special case of the latter definition where "R" is given the trivial grading (every element of "R" is of grade 0).
Examples of graded algebras are common in mathematics:
Graded algebras are much used in commutative algebra
and algebraic geometry
, homological algebra
and algebraic topology
. One example is the close relationship between homogeneous polynomial
s and projective varieties.
G as an index set. A G-graded ring A is a ring with a direct sum decomposition
such that
The notion of "graded ring" now becomes the same thing as a N-graded ring, where N is the monoid of non-negative integers
under addition. The definitions for graded modules and algebras can also be extended this way replacing the indexing set N with any monoid G.
Remarks:
Examples:
In category theory
, a G-graded algebra A is an object in the category of G-graded vector spaces, together with a morphism
of the degree of the identity of G.
to supply the gradation rather than a monoid. Specifically, a signed semiring consists of a pair (Γ, ε) where Γ is a semiring
and ε : Γ → Z/2Z is a homomorphism
of additive monoids. An anticommutative Γ-graded ring is a ring A graded with respect to the additive structure on Γ such that:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a graded algebra is an algebra over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
(or commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
) with an extra piece of structure, known as a gradation (or grading).
The grading is a direct sum decomposition of the algebra with factors indexed in a special way by a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. Given a pair of elements from two factors of the grading, the indexing allows one to know which factor of the grading will contain the product of the chosen elements.
Graded rings
A graded ring A is a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
that has a direct sum decomposition into (abelian) additive groups
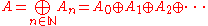
such that the ring multiplication satisfies
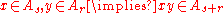
and so
Elements of
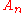are known as homogeneous elements of degree n. An idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
or other subset
⊂ A is homogeneous if for every element a ∈ , the homogeneous parts of a are also contained in If I is a homogeneous ideal in A, then
is also a graded ring, and has decomposition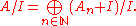Any (non-graded) ring A can be given a gradation by letting A0 = A, and Ai = 0 for i > 0. This is called the trivial gradation on A.
Graded modules
The corresponding idea in module theory is that of a graded module, namely a moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M over a graded ring A such that also
and
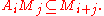
This idea is much used in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, and elsewhere, to define under mild hypotheses a Hilbert function, namely the length
Length of a module
In abstract algebra, the length of a module is a measure of the module's "size". It is defined to be the length of the longest chain of submodules and is a generalization of the concept of dimension for vector spaces...
of Mn as a function of n. Again under mild hypotheses of finiteness, this function is a polynomial, the Hilbert polynomial
Hilbert polynomial
In commutative algebra, the Hilbert polynomial of a graded commutative algebra or graded module is a polynomial in one variable that measures the rate of growth of the dimensions of its homogeneous components...
, for all large enough values of n (see also Hilbert-Samuel polynomial).
Graded algebras
An algebra A over a ring R is a graded algebra if it is graded as a ring. In the case where the ring R is also a graded ring, then one requires that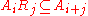and
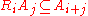
Note that the definition of the graded ring over a ring with no grading is the special case of the latter definition where "R" is given the trivial grading (every element of "R" is of grade 0).
Examples of graded algebras are common in mathematics:
- Polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s. The homogeneous elements of degree n are exactly the homogeneous polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s of degree n. - The tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T•V of a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V. The homogeneous elements of degree n are the tensors of rank n, TnV. - The exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
Λ•V and symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
S•V are also graded algebras. - The cohomology ringCohomology ringIn mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
H• in any cohomology theory is also graded, being the direct sum of the Hn.
Graded algebras are much used in commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. One example is the close relationship between homogeneous polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s and projective varieties.
G-graded rings and algebras
We can generalize the definition of a graded ring using any monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
G as an index set. A G-graded ring A is a ring with a direct sum decomposition
such that
The notion of "graded ring" now becomes the same thing as a N-graded ring, where N is the monoid of non-negative integers
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
under addition. The definitions for graded modules and algebras can also be extended this way replacing the indexing set N with any monoid G.
Remarks:
- If we do not require that the ring have an identity element, semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s may replace monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s.
Examples:
- A group naturally grades the corresponding group ringGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
; similarly, monoid rings are graded by the corresponding monoid. - A superalgebraSuperalgebraIn mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
is another term for a Z2Cyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
-graded algebra. Examples include Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s. Here the homogeneous elements are either of degree 0 (even) or 1 (odd).
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a G-graded algebra A is an object in the category of G-graded vector spaces, together with a morphism
of the degree of the identity of G.Anticommutativity
Some graded rings (or algebras) are endowed with an anticommutative structure. This notion requires the use of a semiringSemiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
to supply the gradation rather than a monoid. Specifically, a signed semiring consists of a pair (Γ, ε) where Γ is a semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
and ε : Γ → Z/2Z is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of additive monoids. An anticommutative Γ-graded ring is a ring A graded with respect to the additive structure on Γ such that:
- xy=(-1)ε (deg x) ε (deg y)yx, for all homogeneous elements x and y.
Examples
- An exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
is an example of an anticommutative algebra, graded with respect to the structure (Z≥ 0, ε) where ε is the homomorphism given by ε(even) = 0, ε(odd) = 1. - A supercommutative algebraSupercommutative algebraIn mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
(sometimes called a skew-commutative associative ring) is the same thing as an anticommutative (Z/2Z, ε) -graded algebra, where ε is the identity endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
for the additive structure.
See also
- Graded vector spaceGraded vector spaceIn mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
- Graded category
- Differential graded algebraDifferential graded algebraIn mathematics, in particular abstract algebra and topology, a differential graded algebra is a graded algebra with an added chain complex structure that respects the algebra structure.- Definition :...
- Graded Lie algebraGraded Lie algebraIn mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
- Filtered algebraFiltered algebraIn mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory....
, a generalization