Projective module
Encyclopedia
In mathematics
, particularly in abstract algebra
and homological algebra
, the concept of projective module over a ring
R is a more flexible generalisation of the idea of a free module
(that is, a module
with basis vectors). Various equivalent characterizations of these modules are available.
Projective modules were first introduced in 1956 in the influential book Homological Algebra by Henri Cartan
and Samuel Eilenberg
.
of the two is a free module F. From this it follows that P is the image of a projection
of F; the module endomorphism in F that is the identity on P and 0 on Q is idempotent and projects F to P.
is to extract the property of lifting, that carries over from free to projective modules. Using a basis of a free module F, it is easy to see that if we are given a surjective module homomorphism from N to M, the corresponding mapping from Hom(F,N) to Hom(F,M) is also surjective (it's from a product of copies of N to the product with the same index set for M). Using the homomorphisms P → F and F → P for a projective module, it is easy to see that P has the same property; and also that if we can lift the identity P → P to P → F for F some free module mapping onto P, that P is a direct summand.
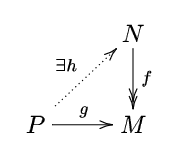
We can summarize this lifting property as follows: a module P is projective if and only if for every surjective module homomorphism f : N ↠ M and every module homomorphism g : P → M, there exists a homomorphism h : P → N such that fh = g. (We don't require the lifting homomorphism h to be unique; this is not a universal property
.)
The advantage of this definition of "projective" is that it can be carried out in categories more general than module categories: we don't need a notion of "free object". It can also be dualized, leading to injective module
s.
For modules, the lifting property can equivalently be expressed as follows: the module P is projective if and only if
for every surjective module homomorphism f : M ↠ P there exists a module homomorphism h : P → M such that fh = idP. The existence of such a section map h implies that P is a direct summand of M and that f is essentially a projection on the summand P. More explicitly, M = im(h) ⊕ ker(f), and im(h) is isomorphic to P.
s. This can be made precise for the ring of continuous real-valued functions on a compact
Hausdorff space
, as well as for the ring of smooth functions on a smooth manifold
(see Swan's theorem
).
Vector bundles are locally free. If there is some notion of "localization" which can be carried over to modules, such as is given at localization of a ring
, one can define locally free modules, and the projective modules then typically coincide with the locally free ones. Specifically, a finitely generated module over a Noetherian ring
is locally free if and only if it is projective. However, there are examples of finitely generated modules over a non-Noetherian ring which are locally free and not projective. For instance,
a Boolean ring
has all of its localizations isomorphic to F2, the field of two elements, so any module over a Boolean ring is locally free, but
there are some non-projective modules over Boolean rings. One example is R/I where
R is a direct product of countably many copies of F2 and I is the direct sum of countably many copies of F2 inside of R.
The R-module R/I is locally free since R is Boolean (and it's finitely generated as an R-module too, with a spanning set of size 1), but R/I is not projective because
I is not a principal ideal. (If a quotient module R/I, for any commutative ring R and ideal I, is a projective R-module then I is principal.) However, it is true that over any commutative ring, R, a finitely presented module is projective if and only if it is locally free if and only if it is a flat module
.
is another deep result; it states that if K is a field
, or more generally a principal ideal domain
, and R = K[X1,...,Xn] is a polynomial ring
over K, then every projective module over R is free.
This problem was first raised by Serre with K a field (and the modules being finitely generated). Bass settled it for non-finitely generated modules and Quillen and Suslin independently and simultaneously treated the case of finitely generated modules. Since every projective module over a principal ideal domain is free, it is attractive to think the following is true: if R is a commutative ring such that every (finitely generated) projective R-module is free then every (finitely generated) projective R[X]-module is free. This is false. A counterexample occurs with R equal to the local ring of the curve y2 = x3 at the origin. So you cannot prove Serre's problem by a simple induction on the number of variables.
of M is an infinite exact sequence
of modules
with all the Pi's projective. Every module possesses a projective resolution. In fact a free resolution (resolution by free module
s) exists. Such an exact sequence may sometimes be seen written as an exact sequence P(M) → M → 0. The minimal length of a finite projective resolution of a module M is called its projective dimension and denoted pd(M). If M does not admit a finite projective resolution then the projective dimension is infinite. A classic example of a projective resolution is given by the Koszul complex
K•(x).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the concept of projective module over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is a more flexible generalisation of the idea of a free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
(that is, a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
with basis vectors). Various equivalent characterizations of these modules are available.
Projective modules were first introduced in 1956 in the influential book Homological Algebra by Henri Cartan
Henri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
and Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
.
Direct summands of free modules
The easiest characterisation is as a direct summand of a free module. That is, a module P is projective provided there is a module Q such that the direct sumDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of the two is a free module F. From this it follows that P is the image of a projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
of F; the module endomorphism in F that is the identity on P and 0 on Q is idempotent and projects F to P.
Lifting property
Another definition that is more in line with category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
is to extract the property of lifting, that carries over from free to projective modules. Using a basis of a free module F, it is easy to see that if we are given a surjective module homomorphism from N to M, the corresponding mapping from Hom(F,N) to Hom(F,M) is also surjective (it's from a product of copies of N to the product with the same index set for M). Using the homomorphisms P → F and F → P for a projective module, it is easy to see that P has the same property; and also that if we can lift the identity P → P to P → F for F some free module mapping onto P, that P is a direct summand.
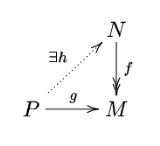
We can summarize this lifting property as follows: a module P is projective if and only if for every surjective module homomorphism f : N ↠ M and every module homomorphism g : P → M, there exists a homomorphism h : P → N such that fh = g. (We don't require the lifting homomorphism h to be unique; this is not a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.)
The advantage of this definition of "projective" is that it can be carried out in categories more general than module categories: we don't need a notion of "free object". It can also be dualized, leading to injective module
Injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
s.
For modules, the lifting property can equivalently be expressed as follows: the module P is projective if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for every surjective module homomorphism f : M ↠ P there exists a module homomorphism h : P → M such that fh = idP. The existence of such a section map h implies that P is a direct summand of M and that f is essentially a projection on the summand P. More explicitly, M = im(h) ⊕ ker(f), and im(h) is isomorphic to P.
Exactness
Perhaps the most insightful and certainly the most abstract characterisation of a projective R-module M is that it has the property that the functor Hom(M,-): R-Mod→ "R"-Mod is (right) exact. (Note that it is always left exact.) Equivalently, we can demand that this functor preserves epi's (surjective homomorphisms) or that it preserves finite colimits. (The equivalence of this last criterion with the lifting property should be clear.)Vector bundles and locally free modules
A basic motivation of the theory is that projective modules (at least over certain commutative rings) are analogues of vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s. This can be made precise for the ring of continuous real-valued functions on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, as well as for the ring of smooth functions on a smooth manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(see Swan's theorem
Swan's theorem
In the mathematical fields of topology and K-theory, the Serre–Swan theorem, also called Swan's theorem, relates the geometric notion of vector bundles to the algebraic concept of projective modules and gives rise to a common intuition throughout mathematics: "projective modules over commutative...
).
Vector bundles are locally free. If there is some notion of "localization" which can be carried over to modules, such as is given at localization of a ring
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
, one can define locally free modules, and the projective modules then typically coincide with the locally free ones. Specifically, a finitely generated module over a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
is locally free if and only if it is projective. However, there are examples of finitely generated modules over a non-Noetherian ring which are locally free and not projective. For instance,
a Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
has all of its localizations isomorphic to F2, the field of two elements, so any module over a Boolean ring is locally free, but
there are some non-projective modules over Boolean rings. One example is R/I where
R is a direct product of countably many copies of F2 and I is the direct sum of countably many copies of F2 inside of R.
The R-module R/I is locally free since R is Boolean (and it's finitely generated as an R-module too, with a spanning set of size 1), but R/I is not projective because
I is not a principal ideal. (If a quotient module R/I, for any commutative ring R and ideal I, is a projective R-module then I is principal.) However, it is true that over any commutative ring, R, a finitely presented module is projective if and only if it is locally free if and only if it is a flat module
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
.
Properties
- Direct sums and direct summands of projective modules are projective.
- If e = e2 is an idempotent in the ring R, then Re is a projective left module over R.
- Submodules of projective modules need not be projective; a ring R for which every submodule of a projective left module is projective is called left hereditaryHereditary ringIn mathematics, especially in the area of abstract algebra known as module theory, a ring R is called hereditary if all submodules of projective modules over R are again projective...
.
- The category of finitely generated projective modules over a ring is an exact categoryExact categoryIn mathematics, an exact category is a concept of category theory due to Daniel Quillen which is designed to encapsulate the properties of short exact sequences in abelian categories without requiring that morphisms actually possess kernels and cokernels, which is necessary for the usual definition...
. (See also algebraic K-theoryAlgebraic K-theoryIn mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
).
- Every module over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
or skew field is projective (even free). A ring over which every module is projective is called semisimple.
- An abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(i.e. a module over ZIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
) is projective if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is a free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
. The same is true for all principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
s; the reason is that for these rings, any submodule of a free module is free.
- Over a Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
a non-principal ideal is always a projective module that is not a free module.
- Over a direct product of rings R × S where R and S are nonzero rings, both R × 0 and 0 × S are non-free projective modules.
- Over a matrix ringMatrix ringIn abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
Mn(R), the natural module Rn is projective but not free. More generally, over any artinianArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
semisimple ring, every module is projective, but the only free proper submodule of the regular module is the zero module.
- Every projective module is flatFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
. The converse is in general not true: the abelian group Q is a Z-module which is flat, but not projective. - In line with the above intuition of "locally free = projective" is the following theorem due to Kaplansky: over a local ringLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
, R, every projective module is free. This is easy to prove for finitely generated projective modules, but the general case is difficult.
Serre's problem
The Quillen–Suslin theoremQuillen–Suslin theorem
The Quillen–Suslin theorem, also known as Serre's problem or Serre's conjecture, is a theorem in commutative algebra about the relationship between free modules and projective modules over polynomial rings...
is another deep result; it states that if K is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, or more generally a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
, and R = K[X1,...,Xn] is a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over K, then every projective module over R is free.
This problem was first raised by Serre with K a field (and the modules being finitely generated). Bass settled it for non-finitely generated modules and Quillen and Suslin independently and simultaneously treated the case of finitely generated modules. Since every projective module over a principal ideal domain is free, it is attractive to think the following is true: if R is a commutative ring such that every (finitely generated) projective R-module is free then every (finitely generated) projective R[X]-module is free. This is false. A counterexample occurs with R equal to the local ring of the curve y2 = x3 at the origin. So you cannot prove Serre's problem by a simple induction on the number of variables.
Projective resolutions
Given a module, M, a projective resolutionResolution (algebra)
In mathematics, particularly in abstract algebra and homological algebra, a resolution is a sequence of objects which is used to describe the structure of a module, or, more generally, the structure of an object in an abelian category.Generally, if the objects involved in the sequence have a...
of M is an infinite exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
of modules
- · · · → Pn → · · · → P2 → P1 → P0 → M → 0,
with all the Pi's projective. Every module possesses a projective resolution. In fact a free resolution (resolution by free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s) exists. Such an exact sequence may sometimes be seen written as an exact sequence P(M) → M → 0. The minimal length of a finite projective resolution of a module M is called its projective dimension and denoted pd(M). If M does not admit a finite projective resolution then the projective dimension is infinite. A classic example of a projective resolution is given by the Koszul complex
Koszul complex
In mathematics, the Koszul complex was first introduced to define a cohomology theory for Lie algebras, by Jean-Louis Koszul...
K•(x).