Universal algebra
Encyclopedia
Universal algebra is the field of mathematics
that studies algebraic structure
s themselves, not examples ("models") of algebraic structures.
For instance, rather than take particular groups as the object of study, in universal algebra one takes "the theory of groups" as an object of study.
operation
on A is a function
that takes n elements of A and returns a single element of A. Thus, a 0-ary operation (or nullary operation) can be represented simply as an element of A, or a constant
, often denoted by a letter like a. A 1-ary operation (or unary operation
) is simply a function from A to A, often denoted by a symbol placed in front of its argument, like ~x. A 2-ary operation (or binary operation
) is often denoted by a symbol placed between its arguments, like x * y. Operations of higher or unspecified arity are usually denoted by function symbols, with the arguments placed in parentheses and separated by commas, like f(x,y,z) or f(x1,...,xn). Some researchers allow infinitary operations, such as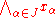
where J is an infinite index set
, thus leading into the algebraic theory of complete lattice
s. One way of talking about an algebra, then, is by referring to it as an algebra of a certain type
, where 
is an ordered sequence of natural numbers representing the arity of the operations of the algebra.
s, which in universal algebra often take the form of identities
, or equational laws. An example is the associative axiom for a binary operation, which is given by the equation x * (y * z) = (x * y) * z. The axiom is intended to hold for all elements x, y, and z of the set A.
, and these are sufficiently important that some authors consider varieties the only object of study in universal algebra, while others consider them an object.
Restricting one's study to varieties rules out:
In this narrower definition, universal algebra can be seen as a special branch of model theory
, in which we are typically dealing with structures having operations only (i.e. the type
can have symbols for functions but not for relations other than equality), and in which the language used to talk about these structures uses equations only.
Not all algebraic structure
s in a wider sense fall into this scope. For example ordered group
s are not studied in mainstream universal algebra because they involve an ordering relation.
A more fundamental restriction is that universal algebra cannot study the class of field
s, because there is no type in which all field laws can be written as equations (inverses of elements are defined for all non-zero elements in a field, so inversion cannot simply be added to the type).
One advantage of this restriction is that the structures studied in universal algebra can be defined in any category
which has finite product
s. For example, a topological group
is just a group in the category of topological space
s.
. Normally a group is defined in terms of a single binary operation *, subject to these axioms:
(Sometimes you will also see an axiom called "closure
", stating that x * y belongs to the set A whenever x and y do. But from a universal algebraist's point of view, that is already implied when you call * a binary operation.)
Now, this definition of a group is problematic from the point of view of universal algebra. The reason is that the axioms of the identity element and inversion are not stated purely in terms of equational laws but also have clauses involving the phrase "there exists ... such that ...". This is inconvenient; the list of group properties can be simplified to universally quantified equations if we add a nullary operation e and a unary operation ~ in addition to the binary operation *, then list the axioms for these three operations as follows: Identity element: e * x = x = x * e.
Inverse element: x * (~x) = e = (~x) * x.
(Of course, we usually write "x −1" instead of "~x", which shows that the notation for operations of low arity
is not always as given in the second paragraph.)
What has changed is that in the usual definition there are:
...while in the universal algebra definition there are
It is important to check that this really does capture the definition of a group. The reason that it might not is that specifying one of these universal groups might give more information than specifying one of the usual kind of group. After all, nothing in the usual definition said that the identity element e was unique; if there is another identity element e, then it is ambiguous which one should be the value of the nullary operator e. However, this is not a problem because identity element
s can be proved to be always unique. The same thing is true of inverse element
s. So the universal algebraist's definition of a group really is equivalent to the usual definition.
, has been fixed. Then there are three basic constructions in universal algebra: homomorphic image, subalgebra, and product.
A homomorphism
between two algebras A and B is a function
h: A → B from the set A to the set B such that, for every operation f (of arity, say, n), h(fA(x1,...,xn)) = fB(h(x1),...,h(xn)). (Here, subscripts are placed on f to indicate whether it is the version of f in A or B. In theory, you could tell this from the context, so these subscripts are usually left off.) For example, if e is a constant (nullary operation), then h(eA) = eB. If ~ is a unary operation, then h(~x) = ~h(x). If * is a binary operation, then h(x * y) = h(x) * h(y). And so on. A few of the things that can be done with homomorphisms, as well as definitions of certain special kinds of homomorphisms, are listed under the entry Homomorphism
. In particular, we can take the homomorphic image of an algebra, h(A).
A subalgebra of A is a subset of A that is closed under all the operations of A. A product of some set of algebraic structures is the cartesian product
of the sets with the operations defined coordinatewise.
It can enable the use of methods invented for some particular classes of algebras to other classes of algebras, by recasting the methods in terms of universal algebra (if possible), and then interpreting these as applied to other classes. It has also provided conceptual clarification; as J.D.H. Smith puts it, "What looks messy and complicated in a particular framework may turn out to be simple and obvious in the proper general one."
In particular, universal algebra can be applied to the study of monoid
s, rings, and lattice
s. Before universal algebra came along, many theorems (most notably the isomorphism theorem
s) were proved separately in all of these fields, but with universal algebra, they can be proven once and for all for every kind of algebraic system.
The 1956 paper by Higgins referenced below has been well followed up for its framweork for a range of particular algebraic systems, while his 1963 paper is notable for its discussion of algebras with operations which are only partially defined, typical examples for this being categories and groupoids. This leads on to the subject of higher dimensional algebra which can be defined as the study of algebraic theories with partial operations whose domains are defined under geometric conditions. Notable examples of these are various forms of higher dimensional categories and groupoids.
.
Given a list of operations and axioms in universal algebra, the corresponding algebras and homomorphisms are the objects and morphisms of a category
.
Category theory applies to many situations where universal algebra does not, extending the reach of the theorems. Conversely, many theorems that hold in universal algebra do not generalise all the way to category theory. Thus both fields of study are useful.
A more recent development in category theory that generalizes operations is operad theory
– an operad is a set of operations, similar to a universal algebra.
's book A Treatise on Universal Algebra, published in 1898, the term universal algebra had essentially the same meaning that it has today. Whitehead credits William Rowan Hamilton
and Augustus De Morgan
as originators of the subject matter, and James Joseph Sylvester
with coining the term itself.
At the time structures such as Lie algebra
s and hyperbolic quaternion
s drew attention to the need to expand algebraic structures beyond the associatively multiplicative class. In a review Alexander Macfarlane
wrote: "The main idea of the work is not unification of the several methods, nor generalization of ordinary algebra so as to include them, but rather the comparative study of their several structures." At the time George Boole
's algebra of logic made a strong counterpoint to ordinary number algebra, so the term "universal" served to calm strained sensibilities.
Whitehead's early work sought to unify quaternions (due to Hamilton), Grassmann's Ausdehnungslehre, and Boole's algebra of logic. Whitehead wrote in his book:
Whitehead, however, had no results of a general nature. Work on the subject was minimal until the early 1930s, when Garrett Birkhoff
and Øystein Ore
began publishing on universal algebras. Developments in metamathematics
and category theory
in the 1940s and 1950s furthered the field, particularly the work of Abraham Robinson
, Alfred Tarski
, Andrzej Mostowski
, and their students (Brainerd 1967).
In the period between 1935 and 1950, most papers were written along the lines suggested by Birkhoff's papers, dealing with free algebras
, congruence and subalgebra lattices, and homomorphism theorems. Although the development of mathematical logic had made applications to algebra possible, they came about slowly; results published by Anatoly Maltsev
in the 1940s went unnoticed because of the war. Tarski's lecture at the 1950 International Congress of Mathematicians
in Cambridge ushered in a new period in which model-theoretic aspects were developed, mainly by Tarski himself, as well as C.C. Chang, Leon Henkin
, Bjarni Jónsson
, Roger Lyndon
, and others.
In the late 1950s, Edward Marczewski
emphasized the importance of free algebras, leading to the publication of more than 50 papers on the algebraic theory of free algebras by Marczewski himself, together with Jan Mycielski
, Władysław Narkiewicz, Witold Nitka, J. Płonka, S. Świerczkowski, K. Urbanik, and others.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
that studies algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s themselves, not examples ("models") of algebraic structures.
For instance, rather than take particular groups as the object of study, in universal algebra one takes "the theory of groups" as an object of study.
Basic idea
From the point of view of universal algebra, an algebra (or algebraic structure) is a set A together with a collection of operations on A. An n-aryArity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
on A is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that takes n elements of A and returns a single element of A. Thus, a 0-ary operation (or nullary operation) can be represented simply as an element of A, or a constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
, often denoted by a letter like a. A 1-ary operation (or unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
) is simply a function from A to A, often denoted by a symbol placed in front of its argument, like ~x. A 2-ary operation (or binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
) is often denoted by a symbol placed between its arguments, like x * y. Operations of higher or unspecified arity are usually denoted by function symbols, with the arguments placed in parentheses and separated by commas, like f(x,y,z) or f(x1,...,xn). Some researchers allow infinitary operations, such as
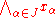where J is an infinite index setIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
, thus leading into the algebraic theory of complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
s. One way of talking about an algebra, then, is by referring to it as an algebra of a certain type
, where is an ordered sequence of natural numbers representing the arity of the operations of the algebra.Equations
After the operations have been specified, the nature of the algebra can be further limited by axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s, which in universal algebra often take the form of identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
, or equational laws. An example is the associative axiom for a binary operation, which is given by the equation x * (y * z) = (x * y) * z. The axiom is intended to hold for all elements x, y, and z of the set A.
Varieties
An algebraic structure which can be defined by identities is called a varietyVariety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
, and these are sufficiently important that some authors consider varieties the only object of study in universal algebra, while others consider them an object.
Restricting one's study to varieties rules out:
- Predicate logicPredicate logicIn mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
, notably quantificationQuantificationQuantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
, including existential quantificationExistential quantificationIn predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
(
) and universal quantificationUniversal quantificationIn predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
(
) - Relations, including inequalities, both
and order relationsOrder theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
In this narrower definition, universal algebra can be seen as a special branch of model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, in which we are typically dealing with structures having operations only (i.e. the type
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
can have symbols for functions but not for relations other than equality), and in which the language used to talk about these structures uses equations only.
Not all algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s in a wider sense fall into this scope. For example ordered group
Ordered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
s are not studied in mainstream universal algebra because they involve an ordering relation.
A more fundamental restriction is that universal algebra cannot study the class of field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s, because there is no type in which all field laws can be written as equations (inverses of elements are defined for all non-zero elements in a field, so inversion cannot simply be added to the type).
One advantage of this restriction is that the structures studied in universal algebra can be defined in any category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
which has finite product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
s. For example, a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is just a group in the category of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s.
Examples
Most of the usual algebraic systems of mathematics are examples of varieties, but not always in an obvious way – the usual definitions often involve quantification or inequalities.Groups
To see how this works, let's consider the definition of a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Normally a group is defined in terms of a single binary operation *, subject to these axioms:
- Associativity (as in the previous section): x * (y * z) = (x * y) * z.
- Identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
: There exists an element e such that for each element x, e * x = x = x * e. - Inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
: It can easily be seen that the identity element is unique. If we denote this unique identity element by e then for each x, there exists an element i such that x * i = e = i * x.
(Sometimes you will also see an axiom called "closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
", stating that x * y belongs to the set A whenever x and y do. But from a universal algebraist's point of view, that is already implied when you call * a binary operation.)
Now, this definition of a group is problematic from the point of view of universal algebra. The reason is that the axioms of the identity element and inversion are not stated purely in terms of equational laws but also have clauses involving the phrase "there exists ... such that ...". This is inconvenient; the list of group properties can be simplified to universally quantified equations if we add a nullary operation e and a unary operation ~ in addition to the binary operation *, then list the axioms for these three operations as follows:
- Associativity:
(Of course, we usually write "x −1" instead of "~x", which shows that the notation for operations of low arity
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
is not always as given in the second paragraph.)
What has changed is that in the usual definition there are:
- a single binary operation (signatureSignature (logic)In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
(2)) - 1 equational law (associativity)
- 2 quantified laws (identity and inverse)
...while in the universal algebra definition there are
- 3 operations: one binary, one unary, and one nullary (signatureSignature (logic)In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
(2,1,0)) - 3 equational laws (associativity, identity, and inverse)
- no quantified laws
It is important to check that this really does capture the definition of a group. The reason that it might not is that specifying one of these universal groups might give more information than specifying one of the usual kind of group. After all, nothing in the usual definition said that the identity element e was unique; if there is another identity element e, then it is ambiguous which one should be the value of the nullary operator e. However, this is not a problem because identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
s can be proved to be always unique. The same thing is true of inverse element
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
s. So the universal algebraist's definition of a group really is equivalent to the usual definition.
Basic constructions
We assume that the type,, has been fixed. Then there are three basic constructions in universal algebra: homomorphic image, subalgebra, and product.A homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
between two algebras A and B is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
h: A → B from the set A to the set B such that, for every operation f (of arity, say, n), h(fA(x1,...,xn)) = fB(h(x1),...,h(xn)). (Here, subscripts are placed on f to indicate whether it is the version of f in A or B. In theory, you could tell this from the context, so these subscripts are usually left off.) For example, if e is a constant (nullary operation), then h(eA) = eB. If ~ is a unary operation, then h(~x) = ~h(x). If * is a binary operation, then h(x * y) = h(x) * h(y). And so on. A few of the things that can be done with homomorphisms, as well as definitions of certain special kinds of homomorphisms, are listed under the entry Homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
. In particular, we can take the homomorphic image of an algebra, h(A).
A subalgebra of A is a subset of A that is closed under all the operations of A. A product of some set of algebraic structures is the cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of the sets with the operations defined coordinatewise.
Some basic theorems
- The Isomorphism theorems, which encompass the isomorphism theorems of groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, ringsRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, modulesModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, etc. - Birkhoff's HSP Theorem, which states that a class of algebras is a varietyVariety (universal algebra)In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
if and only if it is closed under homomorphic images, subalgebras, and arbitrary direct products.
Motivations and applications
In addition to its unifying approach, universal algebra also gives deep theorems and important examples and counterexamples. It provides a useful framework for those who intend to start the study of new classes of algebras.It can enable the use of methods invented for some particular classes of algebras to other classes of algebras, by recasting the methods in terms of universal algebra (if possible), and then interpreting these as applied to other classes. It has also provided conceptual clarification; as J.D.H. Smith puts it, "What looks messy and complicated in a particular framework may turn out to be simple and obvious in the proper general one."
In particular, universal algebra can be applied to the study of monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, rings, and lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
s. Before universal algebra came along, many theorems (most notably the isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
s) were proved separately in all of these fields, but with universal algebra, they can be proven once and for all for every kind of algebraic system.
The 1956 paper by Higgins referenced below has been well followed up for its framweork for a range of particular algebraic systems, while his 1963 paper is notable for its discussion of algebras with operations which are only partially defined, typical examples for this being categories and groupoids. This leads on to the subject of higher dimensional algebra which can be defined as the study of algebraic theories with partial operations whose domains are defined under geometric conditions. Notable examples of these are various forms of higher dimensional categories and groupoids.
Category theory and operads
A more generalised programme along these lines is carried out by category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Given a list of operations and axioms in universal algebra, the corresponding algebras and homomorphisms are the objects and morphisms of a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Category theory applies to many situations where universal algebra does not, extending the reach of the theorems. Conversely, many theorems that hold in universal algebra do not generalise all the way to category theory. Thus both fields of study are useful.
A more recent development in category theory that generalizes operations is operad theory
Operad theory
Operad theory is a field of abstract algebra concerned with prototypical algebras that model properties such as commutativity or anticommutativity as well as various amounts of associativity. Operads generalize the various associativity properties already observed in algebras and coalgebras such as...
– an operad is a set of operations, similar to a universal algebra.
History
In Alfred North WhiteheadAlfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
's book A Treatise on Universal Algebra, published in 1898, the term universal algebra had essentially the same meaning that it has today. Whitehead credits William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
and Augustus De Morgan
Augustus De Morgan
Augustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....
as originators of the subject matter, and James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
with coining the term itself.
At the time structures such as Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and hyperbolic quaternion
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
s drew attention to the need to expand algebraic structures beyond the associatively multiplicative class. In a review Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
wrote: "The main idea of the work is not unification of the several methods, nor generalization of ordinary algebra so as to include them, but rather the comparative study of their several structures." At the time George Boole
George Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
's algebra of logic made a strong counterpoint to ordinary number algebra, so the term "universal" served to calm strained sensibilities.
Whitehead's early work sought to unify quaternions (due to Hamilton), Grassmann's Ausdehnungslehre, and Boole's algebra of logic. Whitehead wrote in his book:
- "Such algebras have an intrinsic value for separate detailed study; also they are worthy of comparative study, for the sake of the light thereby thrown on the general theory of symbolic reasoning, and on algebraic symbolism in particular. The comparative study necessarily presupposes some previous separate study, comparison being impossible without knowledge."
Whitehead, however, had no results of a general nature. Work on the subject was minimal until the early 1930s, when Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
and Øystein Ore
Øystein Ore
Øystein Ore was a Norwegian mathematician.-Life:Ore was graduated from the University of Oslo in 1922, with a Cand.Scient. degree in mathematics. In 1924, the University of Oslo awarded him the Ph.D. for a thesis titled Zur Theorie der algebraischen Körper, supervised by Thoralf Skolem...
began publishing on universal algebras. Developments in metamathematics
Metamathematics
Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
and category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
in the 1940s and 1950s furthered the field, particularly the work of Abraham Robinson
Abraham Robinson
Abraham Robinson was a mathematician who is most widely known for development of non-standard analysis, a mathematically rigorous system whereby infinitesimal and infinite numbers were incorporated into mathematics....
, Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
, Andrzej Mostowski
Andrzej Mostowski
Andrzej Mostowski was a Polish mathematician. He is perhaps best remembered for the Mostowski collapse lemma....
, and their students (Brainerd 1967).
In the period between 1935 and 1950, most papers were written along the lines suggested by Birkhoff's papers, dealing with free algebras
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
, congruence and subalgebra lattices, and homomorphism theorems. Although the development of mathematical logic had made applications to algebra possible, they came about slowly; results published by Anatoly Maltsev
Anatoly Maltsev
Anatoly Ivanovich Maltsev was born in Misheronsky, near Moscow, and died in Novosibirsk, USSR. He was a mathematician noted for his work on the decidability of various algebraic groups...
in the 1940s went unnoticed because of the war. Tarski's lecture at the 1950 International Congress of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
in Cambridge ushered in a new period in which model-theoretic aspects were developed, mainly by Tarski himself, as well as C.C. Chang, Leon Henkin
Leon Henkin
Leon Albert Henkin was a logician at the University of California, Berkeley. He was principally known for the "Henkin's completeness proof": his version of the proof of the semantic completeness of standard systems of first-order logic.-The completeness proof:Henkin's result was not novel; it had...
, Bjarni Jónsson
Bjarni Jónsson
Bjarni Jónsson is an Icelandic mathematician and logician working in universal algebra and lattice theory. He is emeritus Distinguished Professor of Mathematics at Vanderbilt University and the honorary editor in chief of Algebra Universalis...
, Roger Lyndon
Roger Lyndon
Roger Conant Lyndon was an American mathematician, for many years a professor at the University of Michigan. He is known for Lyndon words, the Curtis–Hedlund–Lyndon theorem, Craig–Lyndon interpolation and the Lyndon–Hochschild–Serre spectral sequence.-Biography:Lyndon was born on December 18, 1917...
, and others.
In the late 1950s, Edward Marczewski
Edward Marczewski
Edward Marczewski was a Polish mathematician. His surname until 1940 was Szpilrajn.Marczewski was a member of the Warsaw School of Mathematics...
emphasized the importance of free algebras, leading to the publication of more than 50 papers on the algebraic theory of free algebras by Marczewski himself, together with Jan Mycielski
Jan Mycielski
Jan Mycielski is a Polish-American mathematician, a professor emeritus of mathematics at the University of Colorado at Boulder....
, Władysław Narkiewicz, Witold Nitka, J. Płonka, S. Świerczkowski, K. Urbanik, and others.
External links
- Algebra Universalis—a journal dedicated to Universal Algebra.