Koszul complex
Encyclopedia
In mathematics
, the Koszul complex was first introduced to define a cohomology theory for Lie algebra
s, by Jean-Louis Koszul
(see Lie algebra cohomology
). It turned out to be a useful general construction in homological algebra
.
, if x is an element of the ring R, multiplication by x is R-linear and so represents an R-module
homomorphism
x:R →R from R to itself. It is useful to throw in zeroes on each end and make this a (free) R-complex:
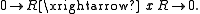
Call this chain complex
K•(x).
Counting the right-hand copy of R as the zeroth degree and the left-hand copy as the first degree, this chain complex neatly captures the most important facts about multiplication by x because its zeroth homology is exactly the homomorphic image of R modulo the multiples of x, H0(K•(x)) = R/xR, and its first homology is exactly the annihilator
of x, H1(K•(x)) = AnnR(x).
This chain complex K•(x) is called the Koszul complex of R with respect to x.
Now, if x1, x2, ..., xn are elements of R, the Koszul complex of R with respect to x1, x2, ..., xn, usually denoted K•(x1, x2, ..., xn), is the tensor product
in the category
of R-complexes of the Koszul complexes defined above individually for each i.
The Koszul complex is a free
chain complex. There are exactly (n choose j) copies of the ring R in the jth degree in the complex (0 ≤ j ≤ n). The matrices involved in the maps can be written down precisely. Letting
denote a free-basis generator in
Kp, d: Kp Kp − 1 is defined by:
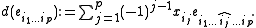
For the case of two elements x and y, the Koszul complex can then be written down quite succinctly as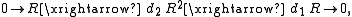
with the matrices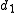
and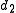 
given by
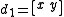and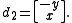
Note that di is applied on the left. The cycles in degree 1 are then exactly the linear relations on the elements x and y, while the boundaries are the trivial relations. The first Koszul homology H1(K•(x, y)) therefore measures exactly the relations mod the trivial relations. With more elements the higher-dimensional Koszul homologies measure the higher-level versions of this.
In the case that the elements x1, x2, ..., xn form a regular sequence
, the higher homology modules of the Koszul complex are all zero.
local ring
with maximal ideal m, and let M be a finitely-generated R-module. If x1, x2, ..., xn are elements of the maximal ideal m, then the following are equivalent:
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Koszul complex was first introduced to define a cohomology theory for Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, by Jean-Louis Koszul
Jean-Louis Koszul
Jean-Louis Koszul is a mathematician best known for studying geometry and discovering the Koszul complex.He was educated at the Lycée Fustel-de-Coulanges in Strasbourg before studying at the Faculty of Science in Strasbourg and the Faculty of Science in Paris...
(see Lie algebra cohomology
Lie algebra cohomology
In mathematics, Lie algebra cohomology is a cohomology theory for Lie algebras. It was defined by in order to give an algebraic construction of the cohomology of the underlying topological spaces of compact Lie groups...
). It turned out to be a useful general construction in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
.
Introduction
In commutative algebraCommutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, if x is an element of the ring R, multiplication by x is R-linear and so represents an R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
x:R →R from R to itself. It is useful to throw in zeroes on each end and make this a (free) R-complex:
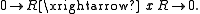
Call this chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
K•(x).
Counting the right-hand copy of R as the zeroth degree and the left-hand copy as the first degree, this chain complex neatly captures the most important facts about multiplication by x because its zeroth homology is exactly the homomorphic image of R modulo the multiples of x, H0(K•(x)) = R/xR, and its first homology is exactly the annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of x, H1(K•(x)) = AnnR(x).
This chain complex K•(x) is called the Koszul complex of R with respect to x.
Now, if x1, x2, ..., xn are elements of R, the Koszul complex of R with respect to x1, x2, ..., xn, usually denoted K•(x1, x2, ..., xn), is the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of R-complexes of the Koszul complexes defined above individually for each i.
The Koszul complex is a free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
chain complex. There are exactly (n choose j) copies of the ring R in the jth degree in the complex (0 ≤ j ≤ n). The matrices involved in the maps can be written down precisely. Letting
denote a free-basis generator inKp, d: Kp Kp − 1 is defined by:
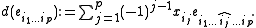
For the case of two elements x and y, the Koszul complex can then be written down quite succinctly as
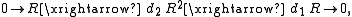
with the matrices
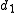and 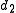given by 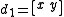and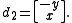Note that di is applied on the left. The cycles in degree 1 are then exactly the linear relations on the elements x and y, while the boundaries are the trivial relations. The first Koszul homology H1(K•(x, y)) therefore measures exactly the relations mod the trivial relations. With more elements the higher-dimensional Koszul homologies measure the higher-level versions of this.
In the case that the elements x1, x2, ..., xn form a regular sequence
Regular sequence (algebra)
In commutative algebra, if R is a commutative ring and M an R-module, a nonzero element r in R is called M-regular if r is not a zerodivisor on M, and M/rM is nonzero...
, the higher homology modules of the Koszul complex are all zero.
Example
If k is a field and X1, X2, ..., Xd are indeterminates and R is the polynomial ring k[X1, X2, ..., Xd], the Koszul complex K•(Xi) on the Xi's forms a concrete free R-resolution of k.Theorem
Let (R, m) be a NoetherianNoetherian
In mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
with maximal ideal m, and let M be a finitely-generated R-module. If x1, x2, ..., xn are elements of the maximal ideal m, then the following are equivalent:
- The (xi) form a regular sequenceRegular sequence (algebra)In commutative algebra, if R is a commutative ring and M an R-module, a nonzero element r in R is called M-regular if r is not a zerodivisor on M, and M/rM is nonzero...
on M, - H1(K•(xi)) = 0,
- Hj(K•(xi)) = 0 for all j ≥ 1.
Applications
The Koszul complex is essential in defining the joint spectrum of a tuple of bounded linear operators in a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.