Coproduct
Encyclopedia
In category theory
, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets
and of topological spaces
, the free product of groups
, and the direct sum
of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion
to the categorical product
, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products.
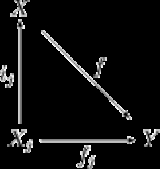
of objects in C. The coproduct of the set {Xj} is an object X together with a collection of morphism
s ij : Xj → X (called canonical injections although they need not be injections
or even monic
) which satisfy a universal property
: for any object Y and any collection of morphisms fj : Xj → Y, there exists a unique morphism f from X to Y such that fj = f ∘ ij. That is, the following diagram commutes
(for each j):

The coproduct of the family {Xj} is often denoted
or
Sometimes the morphism f may be denoted
to indicate its dependence on the individual fj.
If the family of objects consists of only two members the coproduct is usually written X1 ∐ X2 or X1 ⊕ X2 or sometimes simply X1 + X2, and the diagram takes the form:
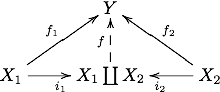
The unique arrow f making this diagram commute is then correspondingly denoted f1 ∐ f2 or f1 ⊕ f2 or f1 + f2 or [f1, f2].
is simply the disjoint union with the maps ij being the inclusion map
s. Unlike direct product
s, coproducts in other categories are not all obviously based on the notion for sets, because unions don't behave well with respect to preserving operations (e.g. the union of two groups need not be a group), and so coproducts in different categories can be dramatically different from each other. For example, the coproduct in the category of groups
, called the free product
, is quite complicated. On the other hand, in the category of abelian groups
(and equally for vector spaces), the coproduct, called the direct sum
, consists of the elements of the direct product which have only finitely many nonzero terms (this therefore coincides exactly with the direct product, in the case of finitely many factors). As a consequence, since most introductory linear algebra
courses deal with only finite-dimension
al vector spaces, nobody really hears much about direct sums until later on.
In the case of topological space
s coproducts are disjoint unions with their disjoint union topologies
. That is, it is a disjoint union of the underlying sets, and the open set
s are sets open in each of the spaces, in a rather evident sense. In the category of pointed space
s, fundamental in homotopy theory, the coproduct is the wedge sum
(which amounts to joining a collection of spaces with base points at a common base point).
Despite all this dissimilarity, there is still, at the heart of the whole thing, a disjoint union: the direct sum of abelian groups is the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero), similarly for vector spaces: the space spanned
by the "almost" disjoint union; the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute.
J into C. Not every family {Xj} will have a coproduct in general, but if it does, then the coproduct is unique in a strong sense: if ij : Xj → X and kj : Xj → Y are two coproducts of the family {Xj}, then (by the definition of coproducts) there exists a unique isomorphism
f : X → Y such that fij = kj for each j in J.
As with any universal property
, the coproduct can be understood as a universal morphism. Let Δ: C → C×C be the diagonal functor which assigns to each object X the ordered pair
(X,X) and to each morphism f:X → Y the pair (f,f). Then the coproduct X+Y in C is given by a universal morphism to the functor Δ from the object (X,Y) in C×C.
The coproduct indexed by the empty set
(that is, an empty coproduct) is the same as an initial object
in C.
If J is a set such that all coproducts for families indexed with J exist, then it is possible to choose the products in a compatible fashion so that the coproduct turns into a functor
CJ → C. The coproduct of the family {Xj} is then often denoted by ∐j Xj, and the maps ij are known as the natural injections.
Letting HomC(U,V) denote the set of all morphisms from U to V in C (that is, a hom-set in C), we have a natural isomorphism
given by the bijection which maps every tuple
of morphisms
(a product in Set, the category of sets
, which is the Cartesian product
, so it is a tuple of morphisms) to the morphism
That this map is a surjection follows from the commutativity of the diagram: any morphism f is the coproduct of the tuple
That it is an injection follows from the universal construction which stipulates the uniqueness of such maps. The naturality of the isomorphism is also a consequence of the diagram. Thus the contravariant hom-functor changes coproducts into products. Stated another way, the hom-functor, viewed as a functor from the opposite category
Copp to Set is continuous; it preserves limits (a coproduct in C is a product in Copp).
If J is a finite set, say J = {1,...,n}, then the coproduct of objects X1,...,Xn is often denoted by X1⊕...⊕Xn.
Suppose all finite coproducts exist in C, coproduct functors have been chosen as above, and 0 denotes the initial object
of C corresponding to the empty coproduct. We then have natural isomorphisms


These properties are formally similar to those of a commutative monoid
; a category with finite coproducts is an example of a symmetric monoidal category
.
If the category has a zero object Z, then we have unique morphism X → Z (since Z is terminal) and thus a morphism X ⊕ Y → Z ⊕ Y. Since Z is also initial, we have a canonical isomorphism Z ⊕ Y ≅ Y as in the preceding paragraph. We thus have morphisms X ⊕ Y → X and X ⊕ Y → Y, by which we infer a canonical morphism X ⊕ Y → X×Y. This may be extended by induction to a canonical morphism from any finite coproduct to the corresponding product. This morphism need not in general be an isomorphism; in Grp it is a proper epimorphism
while in Set* (the category of pointed set
s) it is a proper monomorphism
. In any preadditive category
, this morphism is an isomorphism and the corresponding object is known as the biproduct
. A category with all finite biproducts is known as an additive category
.
If all families of objects indexed by J have coproducts in C, then the coproduct comprises a functor CJ → C. Note that, like the product, this functor is covariant.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
and of topological spaces
Disjoint union (topology)
In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
, the free product of groups
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
, and the direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
to the categorical product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products.
Definition
The formal definition is as follows: Let C be a category and let {Xj : j ∈ J} be an indexed familyIndex set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
of objects in C. The coproduct of the set {Xj} is an object X together with a collection of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s ij : Xj → X (called canonical injections although they need not be injections
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
or even monic
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
) which satisfy a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: for any object Y and any collection of morphisms fj : Xj → Y, there exists a unique morphism f from X to Y such that fj = f ∘ ij. That is, the following diagram commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
(for each j):

The coproduct of the family {Xj} is often denoted

or

Sometimes the morphism f may be denoted

to indicate its dependence on the individual fj.
If the family of objects consists of only two members the coproduct is usually written X1 ∐ X2 or X1 ⊕ X2 or sometimes simply X1 + X2, and the diagram takes the form:

The unique arrow f making this diagram commute is then correspondingly denoted f1 ∐ f2 or f1 ⊕ f2 or f1 + f2 or [f1, f2].
Examples
The coproduct in the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
is simply the disjoint union with the maps ij being the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
s. Unlike direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
s, coproducts in other categories are not all obviously based on the notion for sets, because unions don't behave well with respect to preserving operations (e.g. the union of two groups need not be a group), and so coproducts in different categories can be dramatically different from each other. For example, the coproduct in the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, called the free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
, is quite complicated. On the other hand, in the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
(and equally for vector spaces), the coproduct, called the direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
, consists of the elements of the direct product which have only finitely many nonzero terms (this therefore coincides exactly with the direct product, in the case of finitely many factors). As a consequence, since most introductory linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
courses deal with only finite-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al vector spaces, nobody really hears much about direct sums until later on.
In the case of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s coproducts are disjoint unions with their disjoint union topologies
Disjoint union (topology)
In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
. That is, it is a disjoint union of the underlying sets, and the open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s are sets open in each of the spaces, in a rather evident sense. In the category of pointed space
Pointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
s, fundamental in homotopy theory, the coproduct is the wedge sum
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
(which amounts to joining a collection of spaces with base points at a common base point).
Despite all this dissimilarity, there is still, at the heart of the whole thing, a disjoint union: the direct sum of abelian groups is the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero), similarly for vector spaces: the space spanned
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
by the "almost" disjoint union; the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute.
Discussion
The coproduct construction given above is actually a special case of a colimit in category theory. The coproduct in a category C can be defined as the colimit of any functor from a discrete categoryDiscrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
J into C. Not every family {Xj} will have a coproduct in general, but if it does, then the coproduct is unique in a strong sense: if ij : Xj → X and kj : Xj → Y are two coproducts of the family {Xj}, then (by the definition of coproducts) there exists a unique isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
f : X → Y such that fij = kj for each j in J.
As with any universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, the coproduct can be understood as a universal morphism. Let Δ: C → C×C be the diagonal functor which assigns to each object X the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
(X,X) and to each morphism f:X → Y the pair (f,f). Then the coproduct X+Y in C is given by a universal morphism to the functor Δ from the object (X,Y) in C×C.
The coproduct indexed by the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
(that is, an empty coproduct) is the same as an initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in C.
If J is a set such that all coproducts for families indexed with J exist, then it is possible to choose the products in a compatible fashion so that the coproduct turns into a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
CJ → C. The coproduct of the family {Xj} is then often denoted by ∐j Xj, and the maps ij are known as the natural injections.
Letting HomC(U,V) denote the set of all morphisms from U to V in C (that is, a hom-set in C), we have a natural isomorphism

given by the bijection which maps every tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
of morphisms

(a product in Set, the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, which is the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, so it is a tuple of morphisms) to the morphism

That this map is a surjection follows from the commutativity of the diagram: any morphism f is the coproduct of the tuple

That it is an injection follows from the universal construction which stipulates the uniqueness of such maps. The naturality of the isomorphism is also a consequence of the diagram. Thus the contravariant hom-functor changes coproducts into products. Stated another way, the hom-functor, viewed as a functor from the opposite category
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
Copp to Set is continuous; it preserves limits (a coproduct in C is a product in Copp).
If J is a finite set, say J = {1,...,n}, then the coproduct of objects X1,...,Xn is often denoted by X1⊕...⊕Xn.
Suppose all finite coproducts exist in C, coproduct functors have been chosen as above, and 0 denotes the initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
of C corresponding to the empty coproduct. We then have natural isomorphisms



These properties are formally similar to those of a commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
; a category with finite coproducts is an example of a symmetric monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
.
If the category has a zero object Z, then we have unique morphism X → Z (since Z is terminal) and thus a morphism X ⊕ Y → Z ⊕ Y. Since Z is also initial, we have a canonical isomorphism Z ⊕ Y ≅ Y as in the preceding paragraph. We thus have morphisms X ⊕ Y → X and X ⊕ Y → Y, by which we infer a canonical morphism X ⊕ Y → X×Y. This may be extended by induction to a canonical morphism from any finite coproduct to the corresponding product. This morphism need not in general be an isomorphism; in Grp it is a proper epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
while in Set* (the category of pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
s) it is a proper monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
. In any preadditive category
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
, this morphism is an isomorphism and the corresponding object is known as the biproduct
Biproduct
In category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
. A category with all finite biproducts is known as an additive category
Additive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
.
If all families of objects indexed by J have coproducts in C, then the coproduct comprises a functor CJ → C. Note that, like the product, this functor is covariant.
See also
- ProductProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
- Limits and colimitsLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
- CoequalizerCoequalizerIn category theory, a coequalizer is a generalization of a quotient by an equivalence relation to objects in an arbitrary category...
- Direct limitDirect limitIn mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
External links
- Interactive Web page which generates examples of coproducts in the category of finite sets. Written by Jocelyn Paine.

