Three-dimensional space
Encyclopedia
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
(without considering time) in which we live. These three dimensions are commonly called length, width, and depth (or height), although any three directions can be chosen, provided that they do not lie in the same plane.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sequence of n numbers
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
can be understood as a location in n-dimensional space. When n = 3, the set of all such locations is called 3-dimensional Euclidean space. As commonly the mathematician symbolizise,
, this space is only one example of a great variety of spaces in three dimensions called 3-manifolds.Details
In physics, our three-dimensional space is viewed as embedded in 4-dimensional space-time, called Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
(see special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
). The idea behind space-time is that time is hyperbolic-orthogonal
Hyperbolic-orthogonal
In plane geometry, two lines are hyperbolic orthogonal when they are reflections of each other over the asymptote of a given hyperbola.Two particular hyperbolas are frequently used in the plane: x y = 1 with y = 0 as asymptote.Two particular hyperbolas are frequently used in the plane: x y = 1 ...
to each of the three spatial dimensions.
In mathematics, analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
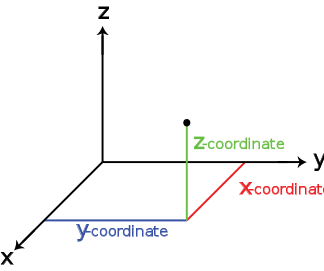
(also called Cartesian geometry) describes every point in three-dimensional space by means of three coordinates. Three coordinate axes are given, usually each perpendicular to the other two at the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, the point at which they cross. They are usually labeled x, y, and z. Relative to these axes, the position of any point in three-dimensional space is given by an ordered triple of real numbers, each number giving the distance of that point from the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
measured along the given axis, which is equal to the distance of that point from the plane determined by the other two axes.
Other popular methods of describing the location of a point in three-dimensional space include cylindrical coordinates and spherical coordinates, though there is an infinite number of possible methods. See Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Another mathematical way of viewing three-dimensional space is found in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, where the idea of independence is crucial. Space has three dimensions because the length of a box
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
is independent of its width or breadth. In the technical language of linear algebra, space is three-dimensional because every point in space can be described by a linear combination of three independent vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
s. In this view, space-time is four-dimensional because the location of a point in time is independent of its location in space.
Three-dimensional space has a number of properties that distinguish it from spaces of other dimension numbers. For example, at least 3 dimensions are required to tie a knot
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
in a piece of string. Many of the laws of physics, such as the various inverse square laws, depend on dimension three.
The understanding of three-dimensional space in humans is thought to be learned during infancy using unconscious inference, and is closely related to hand-eye coordination. The visual ability to perceive the world in three dimensions is called depth perception
Depth perception
Depth perception is the visual ability to perceive the world in three dimensions and the distance of an object. Depth sensation is the ability to move accurately, or to respond consistently, based on the distances of objects in an environment....
.
With the space
, the topologists locally model all other 3-manifolds.Polytopes
In three dimensions, there are nine regular polytopes: five convex and four nonconvex. The convex ones are the Platonic solids while the nonconvex ones are the Kepler-Poinsot polyhedra.Hypersphere
A hypersphereHypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
in 3-space (also called a 2-sphere because its surface is 2-dimensional) consists of the set of all points in 3-space at a fixed distance r from a central point P. The volume enclosed by this surface is:
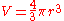
Another hypersphere, but having three dimensions is the 3-sphere: points equidistant to the origin of the euclidean space
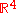at distance one. If any position is 
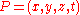, then 
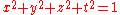characterize a point in the 3-sphere.Orthogonality
In the familiar 3-dimensional space that we live in, there are three pairs of cardinal directions: up/down (altitude), north/south (latitude), and east/west (longitude). These pairs of directions are mutually orthogonal: They are at right angles to each other. In mathematical terms, they lie on three coordinate axes, usually labelled x, y, and z. The z-buffer in computer graphics refers to this z-axis, representing depth in the 2-dimensional imagery displayed on the computer screen.Coordinate systems
In mathematics, analytic geometryAnalytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
(also called Cartesian geometry) describes every point in three-dimensional space by means of three coordinates. Three coordinate axes are given, each perpendicular to the other two at the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, the point at which they cross. They are usually labeled x, y, and z. Relative to these axes, the position of any point in three-dimensional space is given by an ordered triple of real numbers, each number giving the distance of that point from the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
measured along the given axis, which is equal to the distance of that point from the plane determined by the other two axes.
Other popular methods of describing the location of a point in three-dimensional space include cylindrical coordinates and spherical coordinates, though there is an infinite number of possible methods. See Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Below are images of the abovementioned systems.
See also
- Three-dimensional graph
- 3D (disambiguation)
- Dimensional analysisDimensional analysisIn physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
- 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s