
Closed timelike curve
Encyclopedia
In mathematical physics
, a closed timelike curve (CTC) is a worldline in a Lorentzian manifold, of a material particle in spacetime
that is "closed," returning to its starting point. This possibility was first raised by Kurt Gödel
in 1949, who discovered a solution to the equations of general relativity
(GR) allowing CTCs known as the Gödel metric
; and since then other GR solutions containing CTCs have been found, such as the Tipler cylinder
and traversable wormholes. If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel
backwards in time, raising the spectre of the grandfather paradox
, although the Novikov self-consistency principle
seems to show that such paradoxes could be avoided. Some physicists speculate that the CTCs which appear in certain GR solutions might be ruled out by a future theory of quantum gravity
which would replace GR, an idea which Stephen Hawking
has labeled the chronology protection conjecture
. Others note that if every closed timelike curve in a given space-time passes through an event horizon, a property which can be called chronological censorship, then that space-time with event horizons excised would still be causally well behaved and an observer might not be able to detect the causal violation.
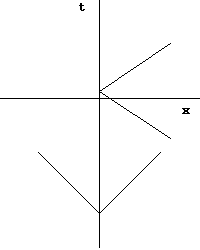 When discussing the evolution of a system in general relativity
When discussing the evolution of a system in general relativity
, or more specifically Minkowski space
, physicists often refer to a "light cone
". A light cone represents any possible future evolution of an object given its current state, or every possible location given its current location. An object's possible future locations are limited by the speed that the object can move, which is at best the speed of light
. For instance, an object located at position p at time t0 can only move to locations within c(t1 − t0) in time t1.
This is commonly represented on a graph with physical locations along the horizontal axis and time running vertically, with units of for time and ct for space. Light cones in this representation appear as lines at 45 degrees centered on the object, as light travels at
for time and ct for space. Light cones in this representation appear as lines at 45 degrees centered on the object, as light travels at 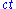 per
per  . On such a diagram, every possible future location of the object lies within the cone. Additionally, every space location has a future time, implying that an object may stay at any location in space indefinitely.
. On such a diagram, every possible future location of the object lies within the cone. Additionally, every space location has a future time, implying that an object may stay at any location in space indefinitely.
Any single point on such a diagram is known as an event. Separate events are considered to be timelike if they are separated across the time axis, or spacelike if they differ along the space axis. If the object were in free fall
it would travel up the t-axis, if it accelerates it moves across the x axis as well. The actual path an object takes through spacetime, as opposed to the ones it could take, is known as the worldline
. Another definition is that the light cone represents all possible worldlines.
In "simple" examples of spacetime metrics
the light cone is directed forward in time. This corresponds to the common case that an object cannot be in two places at once, or alternately that it cannot move instantly to another location. In these spacetimes, the worldlines of physical objects are, by definition, timelike. However this orientation is only true of "locally flat" spacetimes. In curved spacetimes the light cone will be "tilted" along the spacetime's geodesic
. For instance, while moving in the vicinity of a star, the star's gravity will "pull" on the object, affecting its worldline, so its possible future positions lie closer to the star. This appears as a slightly tilted lightcone on the corresponding spacetime diagram. An object in free fall in this circumstance continues to move along its local axis, but to an external observer it appears it is accelerating in space as well—a common situation if the object is in orbit, for instance.
axis, but to an external observer it appears it is accelerating in space as well—a common situation if the object is in orbit, for instance.
In extreme examples, in spacetimes with suitably high-curvature metrics, the light cone can be tilted beyond 45 degrees. That means there are potential "future" positions, from the object's frame of reference, that are spacelike separated to observers in an external rest frame
. From this outside viewpoint, the object can move instantaneously through space. In these situations the object would have to move, since its present spatial location would not be in its own future light cone. Additionally, with enough of a tilt, there are event locations that lie in the "past" as seen from the outside. With a suitable movement of what appears to it its own space axis, the object appears to travel though time as seen externally.
A closed timelike curve can be created if a series of such light cones are set up so as to loop back on themselves, so it would be possible for an object to move around this loop and return to the same place and time that it started. An object in such an orbit would repeatedly return to the same point in spacetime if it stays in free fall. Returning to the original spacetime location would be only one possibility; the object's future light cone would include spacetime points both forwards and backwards in time, and so it should be possible for the object to engage in time travel
under these conditions.
to the Einstein field equation of general relativity
, including some of the most important solutions. These include:
Some of these examples are, like the Tipler cylinder, rather artificial, but the exterior part of the Kerr solution is thought to be in some sense generic, so it is rather unnerving to learn that its interior contains CTCs. Most physicists feel that CTCs in such solutions are artifacts.
demands that each event in spacetime is preceded by its cause in every rest frame. This principle is critical in determinism
, which in the language of general relativity
states complete knowledge of the universe on a spacelike Cauchy surface
can be used to calculate the complete state of the rest of spacetime. However, in a CTC, causality breaks down, because an event can be "simultaneous" with its cause—in some sense an event may be able to cause itself. It is impossible to determine based only on knowledge of the past whether or not something exists in the CTC that can interfere with other objects in spacetime. A CTC therefore results in a Cauchy horizon
, and a region of spacetime that cannot be predicted from perfect knowledge of some past time.
No CTC can be continuously deformed as a CTC to a point (that is, a CTC and a point are not timelike homotopic), as the manifold would not be causally well behaved at that point. The topological feature which prevents the CTC from being deformed to a point is known as a timelike topological feature.
Existence of CTCs places restrictions on physically allowable states of matter-energy fields in the universe. Propagating a field configuration along the family of closed timelike worldlines must eventually result in the state that is identical to the original one. This has been explored by some scientists as a possible approach towards disproving the existence of CTCs.
among timelike curves, as that point would not be causally well behaved.
. The Cauchy horizon is generated by closed null geodesics. Associated with each closed null geodesic is a redshift factor describing the rescaling of the rate of change of the affine parameter around a loop. Because of this redshift factor, the affine parameter terminates at a finite value after infinitely many revolutions because the geometric series converges.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, a closed timelike curve (CTC) is a worldline in a Lorentzian manifold, of a material particle in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
that is "closed," returning to its starting point. This possibility was first raised by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in 1949, who discovered a solution to the equations of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
(GR) allowing CTCs known as the Gödel metric
Gödel metric
The Gödel metric is an exact solution of the Einstein field equations in which the stress-energy tensor contains two terms, the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a nonzero cosmological constant...
; and since then other GR solutions containing CTCs have been found, such as the Tipler cylinder
Tipler Cylinder
A Tipler cylinder is a cylinder of dense matter of infinite length, rotating about its longitudinal axis. This hypothetical object is theorized to allow time travel and is also called a Tipler time machine....
and traversable wormholes. If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel
Time travel
Time travel is the concept of moving between different points in time in a manner analogous to moving between different points in space. Time travel could hypothetically involve moving backward in time to a moment earlier than the starting point, or forward to the future of that point without the...
backwards in time, raising the spectre of the grandfather paradox
Grandfather paradox
The grandfather paradox is a proposed paradox of time travel first described by the science fiction writer René Barjavel in his 1943 book Le Voyageur Imprudent . The paradox is this: suppose a man traveled back in time and killed his biological grandfather before the latter met the traveler's...
, although the Novikov self-consistency principle
Novikov self-consistency principle
The Novikov self-consistency principle, also known as the Novikov self-consistency conjecture, is a principle developed by Russian physicist Igor Dmitriyevich Novikov in the mid-1980s to solve the problem of paradoxes in time travel, which is theoretically permitted in certain solutions of general...
seems to show that such paradoxes could be avoided. Some physicists speculate that the CTCs which appear in certain GR solutions might be ruled out by a future theory of quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
which would replace GR, an idea which Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
has labeled the chronology protection conjecture
Chronology protection conjecture
The chronology protection conjecture is a conjecture by the physicist Professor Stephen Hawking that the laws of physics are such as to prevent time travel on all but sub-microscopic scales. Mathematically, the permissibility of time travel is represented by the existence of closed timelike curves...
. Others note that if every closed timelike curve in a given space-time passes through an event horizon, a property which can be called chronological censorship, then that space-time with event horizons excised would still be causally well behaved and an observer might not be able to detect the causal violation.
Light cones

General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, or more specifically Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, physicists often refer to a "light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
". A light cone represents any possible future evolution of an object given its current state, or every possible location given its current location. An object's possible future locations are limited by the speed that the object can move, which is at best the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. For instance, an object located at position p at time t0 can only move to locations within c(t1 − t0) in time t1.
This is commonly represented on a graph with physical locations along the horizontal axis and time running vertically, with units of
 for time and ct for space. Light cones in this representation appear as lines at 45 degrees centered on the object, as light travels at
for time and ct for space. Light cones in this representation appear as lines at 45 degrees centered on the object, as light travels at 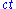 per
per  . On such a diagram, every possible future location of the object lies within the cone. Additionally, every space location has a future time, implying that an object may stay at any location in space indefinitely.
. On such a diagram, every possible future location of the object lies within the cone. Additionally, every space location has a future time, implying that an object may stay at any location in space indefinitely.Any single point on such a diagram is known as an event. Separate events are considered to be timelike if they are separated across the time axis, or spacelike if they differ along the space axis. If the object were in free fall
Free fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
it would travel up the t-axis, if it accelerates it moves across the x axis as well. The actual path an object takes through spacetime, as opposed to the ones it could take, is known as the worldline
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
. Another definition is that the light cone represents all possible worldlines.
In "simple" examples of spacetime metrics
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
the light cone is directed forward in time. This corresponds to the common case that an object cannot be in two places at once, or alternately that it cannot move instantly to another location. In these spacetimes, the worldlines of physical objects are, by definition, timelike. However this orientation is only true of "locally flat" spacetimes. In curved spacetimes the light cone will be "tilted" along the spacetime's geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
. For instance, while moving in the vicinity of a star, the star's gravity will "pull" on the object, affecting its worldline, so its possible future positions lie closer to the star. This appears as a slightly tilted lightcone on the corresponding spacetime diagram. An object in free fall in this circumstance continues to move along its local
 axis, but to an external observer it appears it is accelerating in space as well—a common situation if the object is in orbit, for instance.
axis, but to an external observer it appears it is accelerating in space as well—a common situation if the object is in orbit, for instance.In extreme examples, in spacetimes with suitably high-curvature metrics, the light cone can be tilted beyond 45 degrees. That means there are potential "future" positions, from the object's frame of reference, that are spacelike separated to observers in an external rest frame
Rest frame
In special relativity the rest frame of a particle is the coordinate system in which the particle is at rest.The rest frame of compound objects is taken to be the frame of reference in which the average momentum of the particles which make up the substance is zero In special relativity the rest...
. From this outside viewpoint, the object can move instantaneously through space. In these situations the object would have to move, since its present spatial location would not be in its own future light cone. Additionally, with enough of a tilt, there are event locations that lie in the "past" as seen from the outside. With a suitable movement of what appears to it its own space axis, the object appears to travel though time as seen externally.
A closed timelike curve can be created if a series of such light cones are set up so as to loop back on themselves, so it would be possible for an object to move around this loop and return to the same place and time that it started. An object in such an orbit would repeatedly return to the same point in spacetime if it stays in free fall. Returning to the original spacetime location would be only one possibility; the object's future light cone would include spacetime points both forwards and backwards in time, and so it should be possible for the object to engage in time travel
Time travel
Time travel is the concept of moving between different points in time in a manner analogous to moving between different points in space. Time travel could hypothetically involve moving backward in time to a moment earlier than the starting point, or forward to the future of that point without the...
under these conditions.
General relativity
CTCs appear in locally unobjectionable exact solutionsExact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
to the Einstein field equation of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, including some of the most important solutions. These include:
- the Misner space (which is Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
orbifoldOrbifoldIn the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
ed by a discrete boost) - the Kerr vacuumKerr metricThe Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
(which models a rotating uncharged black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
) - the interior of a rotating BTZ black holeBTZ black holeThe BTZ black hole, named after Maximo Banados, Claudio Teitelboim, and Jorge Zanelli, is a black hole solution for -dimensional gravity with a negative cosmological constant....
- the van Stockum dustVan Stockum dustIn general relativity, the van Stockum dust is an exact solution of the Einstein field equation in which the gravitational field is generated by dust rotating about an axis of cylindrical symmetry...
(which models a cylindrically symmetric configuration of dustDust solutionIn general relativity, a dust solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid which has positive mass density but vanishing pressure...
) - the Gödel lambdadustGödel metricThe Gödel metric is an exact solution of the Einstein field equations in which the stress-energy tensor contains two terms, the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a nonzero cosmological constant...
(which models a dust with a carefully chosen cosmological constant term) - the Tipler cylinderTipler CylinderA Tipler cylinder is a cylinder of dense matter of infinite length, rotating about its longitudinal axis. This hypothetical object is theorized to allow time travel and is also called a Tipler time machine....
(a cylindrically symmetric metric with CTCs) - Bonnor Steadman solutions describing laboratory situations such as two spinning balls
- J. Richard GottJ. Richard GottJohn Richard Gott III is a professor of astrophysical sciences at Princeton University. He is known for developing and advocating two cosmological theories with the flavor of science fiction: Time travel and the Doomsday argument.- Exotic matter time travel theories :Paul Davies's bestseller How...
has proposed a mechanism for creating CTCs using cosmic strings.
Some of these examples are, like the Tipler cylinder, rather artificial, but the exterior part of the Kerr solution is thought to be in some sense generic, so it is rather unnerving to learn that its interior contains CTCs. Most physicists feel that CTCs in such solutions are artifacts.
Consequences
One feature of a CTC is that it opens the possibility of a worldline which is not connected to earlier times, and so the existence of events that cannot be traced to an earlier cause. Ordinarily, causalityCausality
Causality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
demands that each event in spacetime is preceded by its cause in every rest frame. This principle is critical in determinism
Determinism
Determinism is the general philosophical thesis that states that for everything that happens there are conditions such that, given them, nothing else could happen. There are many versions of this thesis. Each of them rests upon various alleged connections, and interdependencies of things and...
, which in the language of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
states complete knowledge of the universe on a spacelike Cauchy surface
Cauchy surface
Intuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
can be used to calculate the complete state of the rest of spacetime. However, in a CTC, causality breaks down, because an event can be "simultaneous" with its cause—in some sense an event may be able to cause itself. It is impossible to determine based only on knowledge of the past whether or not something exists in the CTC that can interfere with other objects in spacetime. A CTC therefore results in a Cauchy horizon
Cauchy horizon
In physics, a Cauchy horizon is a light-like boundary of the domain of validity of a Cauchy problem...
, and a region of spacetime that cannot be predicted from perfect knowledge of some past time.
No CTC can be continuously deformed as a CTC to a point (that is, a CTC and a point are not timelike homotopic), as the manifold would not be causally well behaved at that point. The topological feature which prevents the CTC from being deformed to a point is known as a timelike topological feature.
Existence of CTCs places restrictions on physically allowable states of matter-energy fields in the universe. Propagating a field configuration along the family of closed timelike worldlines must eventually result in the state that is identical to the original one. This has been explored by some scientists as a possible approach towards disproving the existence of CTCs.
Contractible versus noncontractible
There are two classes of CTCs. We have CTCs contractible to a point (if we no longer insist it has to be future-directed timelike everywhere), and we have CTCs which are not contractible. For the latter, we can always go to the universal covering space, and reestablish causality. For the former, such a procedure is not possible. No closed timelike curve is contractible to a point by a timelike homotopyTimelike homotopy
On a Lorentzian manifold, certain curves are distinguished as timelike. A timelike homotopy between two timelike curves is a homotopy such that each intermediate curve is timelike...
among timelike curves, as that point would not be causally well behaved.
Cauchy horizon
The chronology violating set is the set of points through which CTCs pass. The boundary of this set is the Cauchy horizonCauchy horizon
In physics, a Cauchy horizon is a light-like boundary of the domain of validity of a Cauchy problem...
. The Cauchy horizon is generated by closed null geodesics. Associated with each closed null geodesic is a redshift factor describing the rescaling of the rate of change of the affine parameter around a loop. Because of this redshift factor, the affine parameter terminates at a finite value after infinitely many revolutions because the geometric series converges.
External links
- A Primer on Time Travel – (backup in the Internet ArchiveInternet ArchiveThe Internet Archive is a non-profit digital library with the stated mission of "universal access to all knowledge". It offers permanent storage and access to collections of digitized materials, including websites, music, moving images, and nearly 3 million public domain books. The Internet Archive...
)

