Regular polytope - AbsoluteAstronomy.com

Regular polytope examples
A regular pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... is a polygon Polygon In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments... , a two-dimensional polytope with 5 edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... , represented by Schläfli symbol {5}.	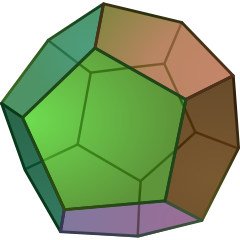A regular dodecahedron is a polyhedron Polyhedron In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges... , a three-dimensional polytope, with 12 pentagonal faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube... , represented by Schläfli symbol {5,3}.
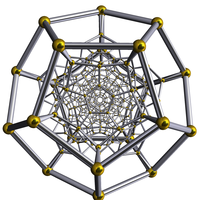A regular dodecaplex is a polychoron Polychoron In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells... , a four-dimensional polytope, with 120 dodecahedral cells Cell (geometry) In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made... , represented by Schläfli symbol {5,3,3}. (shown here as a Schlegel diagram)	A regular cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... is a tessellation Tessellation A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art... , an infinite three-dimensional polytope,represented by Schläfli symbol {4,3,4}.
The 256 vertices and 1024 edges of an 8-cube can be shown in this orthogonal projection (Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... )

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a regular polytope is a polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

whose symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces (for all 0 ≤ j ≤ n, where n is the dimension of the polytope) — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of dimension ≤ n.

Regular polytopes are the generalized analog in any number of dimensions of regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

s (for example, the square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

or the regular pentagon) and regular polyhedra (for example, the cube

Cube

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...

). The strong symmetry of the regular polytopes gives them an aesthetic

Aesthetics

Aesthetics is a branch of philosophy dealing with the nature of beauty, art, and taste, and with the creation and appreciation of beauty. It is more scientifically defined as the study of sensory or sensori-emotional values, sometimes called judgments of sentiment and taste...

quality that interests both non-mathematicians and mathematicians.

Classically, a regular polytope in n dimensions may be defined as having regular facets [(n − 1)-faces] and regular vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

s. These two conditions are sufficient to ensure that all faces are alike and all vertices are alike. Note, however, that this definition does not work for abstract polytope

Abstract polytope

In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...

s.

A regular polytope can be represented by a Schläfli symbol of the form {a, b, c, ...., y, z}, with regular facets as {a, b, c, ..., y}, and regular vertex figures as {b, c, ..., y, z}.

Classification and description

Regular polytopes are classified primarily according to their dimensionality.

They can be further classified according to symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

. For example the cube

Cube

and the regular octahedron

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

share the same symmetry, as do the regular dodecahedron and icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

. Indeed, symmetry groups are sometimes named after regular polytopes, for example the tetrahedral and icosahedral symmetries.

Three special classes of regular polytope exist in every dimensionality:

Regular simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
Measure polytope (Hypercube)
Cross polytope (Orthoplex)

In two dimensions there are infinitely many regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

s. In three and four dimensions there are several more regular polyhedra

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

and polychora

Polychoron

In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...

besides these three. In five dimensions and above, these are the only ones. See also the list of regular polytopes.

The idea of a polytope is sometimes generalised to include related kinds of geometrical object. Some of these have regular examples, as discussed in the section on historical discovery below.

Schläfli symbols

A concise symbolic representation for regular polytopes was developed by Ludwig Schläfli in the 19th Century, and a slightly modified form has become standard. The notation is best explained by adding one dimension at a time.

A convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...

regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

having n sides is denoted by {n}. So an equilateral triangles is {3}, a square {4}, and so on indefinitely. A regular star polygon which winds m times around its centre is denoted by the fractional value {n/m}, where n and m are co-prime, so a regular pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...

is {5/2}.

A regular polyhedron
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

having faces {n} with p faces joining around a vertex is denoted by {n, p}. The nine regular polyhedra
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

are {3, 3} {3, 4} {4, 3} {3, 5} {5, 3} {3, 5/2} {5/2, 3} {5, 5/2} and {5/2, 5}. {p} is the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

of the polyhedron.

A regular polychoron or polycell having cells {n, p} with q cells joining around an edge is denoted by {n, p, q}. The vertex figure of the polychoron is a {p, q}.

A five-dimensional regular polytope is an {n, p, q, r}. And so on.

Duality of the regular polytopes

The dual of a regular polytope is also a regular polytope. The Schläfli symbol for the dual polytope is just the original symbol written backwards: {3, 3} is self-dual, {3, 4} is dual to {4, 3}, {4, 3, 3} to {3, 3, 4} and so on.

The vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

of a regular polytope is the dual of the dual polytope's facet. For example, the vertex figure of {3, 3, 4} is {3, 4}, the dual of which is {4, 3} — a cell

Cell (geometry)

In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...

of {4, 3, 3}.

The measure

Hypercube

In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...

and cross polytopes in any dimension are dual to each other.

If the Schläfli symbol is palindromic

Palindrome

A palindrome is a word, phrase, number, or other sequence of units that can be read the same way in either direction, with general allowances for adjustments to punctuation and word dividers....

, i.e. reads the same forwards and backwards, then the polyhedron is self-dual. The self-dual regular polytopes are:

All regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

s, {a}.
All regular n-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

es, {3,3,...,3}
The regular 24-cell in 4 dimensions, {3,4,3}.
All regular n-dimensional cubic honeycombs
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....

, {4,3,...,3,4}. These may be treated as infinite polytopes.

Regular simplices

Graphs of the 1-simplex to 4-simplex.

Line segment Line segment In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...	Triangle	Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	Pentachoron Pentachoron In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid...

Begin with a point A. Mark point B at a distance r from it, and join to form a line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

. Mark point C in a second, orthogonal, dimension at a distance r from both, and join to A and B to form an equilateral triangle. Mark point D in a third, orthogonal, dimension a distance r from all three, and join to form a regular tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

. And so on for higher dimensions.

These are the regular simplices or simplexes. Their names are, in order of dimensionality:

0. Point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

1. Line segment

Line segment

2. Equilateral triangle (regular trigon)

3. Regular tetrahedron

Tetrahedron

4. Regular pentachoron

Pentachoron

In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as the pentachoron, pentatope, or hyperpyramid...

or 4-simplex

5. Regular hexateron

Hexateron

In five dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has 6 vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 pentachoron facets. It has a dihedral angle of cos−1, or approximately 78.46°.- Alternate names :...

or 5-simplex

... An n-simplex has n+1 vertices.

Measure polytopes (hypercubes)

Graphs of the 2-cube to 4-cube.

Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...	Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...	Tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

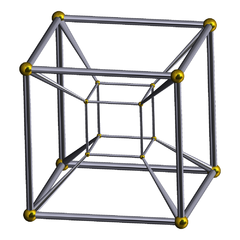Begin with a point A. Extend a line to point B at distance r, and join to form a line segment. Extend a second line of length r, orthogonal to AB, from B to C, and likewise from A to D, to form a square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

ABCD. Extend lines of length r respectively from each corner, orthogonal to both AB and BC (i.e. upwards). Mark new points E,F,G,H to form the cube

Cube

ABCDEFGH. And so on for higher dimensions.

These are the measure polytopes or hypercubes. Their names are, in order of dimensionality:

0. Point

1. Line segment

2. Square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

(regular tetragon)

3. Cube

Cube

(regular hexahedron)

4. Tesseract

Tesseract

In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...

(regular octachoron) or 4-cube

5. Penteract

Penteract

In five dimensional geometry, a 5-cube is a name for a five dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract hypercells....

(regular decateron) or 5-cube

... An n-cube has 2ⁿ vertices.

Cross polytopes (orthoplexes)

Graphs of the 2-orthoplex to 4-orthoplex.

Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...	Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	16-cell 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

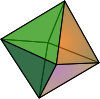Begin with a point O. Extend a line in opposite directions to points A and B a distance r from O and 2r apart. Draw a line COD of length 2r, centred on O and orthogonal to AB. Join the ends to form a square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

ACBD. Draw a line EOF of the same length and centered on 'O', orthogonal to AB and CD (i.e. upwards and downwards). Join the ends to the square to form a regular octahedron

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

. And so on for higher dimensions.

These are the cross polytopes or orthoplexes. Their names are, in order of dimensionality:

0. Point

1. Line segment

2. Square (regular tetragon)

3. Regular octahedron

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

4. Regular hexadecachoron (16-cell

16-cell

In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....

) or 4-orthoplex

5. Regular triacontakaiditeron (Pentacross

Pentacross

In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell hypercells....

) or 5-orthoplex

... An n-orthoplex has 2n vertices.

Convex polygons and polyhedra

The earliest surviving mathematical treatment of regular polygons and polyhedra comes to us from ancient Greek

Ancient Greece

Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...

mathematicians. The five Platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s were known to them. Pythagoras

Pythagoras

Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...

knew of at least three of them and Theaetetus

Theaetetus (mathematician)

Theaetetus, Theaitētos, of Athens, possibly son of Euphronius, of the Athenian deme Sunium, was a classical Greek mathematician...

(ca. 417 B.C. – 369 B.C.) described all five. Later, Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

wrote a systematic study of mathematics, publishing it under the title Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...

, which built up a logical theory of geometry and number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

. His work concluded with mathematical descriptions of the five Platonic solid

Platonic solid

Platonic solid Platonic solid In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and... s

Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...	Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	Dodecahedron	Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

Star polygons and polyhedra

Our understanding remained static for many centuries after Euclid. The subsequent history of the regular polytopes can be characterised by a gradual broadening of the basic concept, allowing more and more objects to be considered among their number. Thomas Bradwardine

Thomas Bradwardine

Thomas Bradwardine was an English scholar, scientist, courtier and, very briefly, Archbishop of Canterbury. As a celebrated scholastic philosopher and doctor of theology, he is often called Doctor Profundus, .-Life:He was born either at Hartfield in Sussex or at Chichester, where his family were...

(Bradwardinus) was the first to record a serious study of star polygons. Various star polyhedra appear in Renaissance art, but it was not until Johannes Kepler

Johannes Kepler

Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...

studied the small stellated dodecahedron and the great stellated dodecahedron in 1619 that he realised these two were regular. Louis Poinsot

Louis Poinsot

Louis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...

discovered the great dodecahedron and great icosahedron in 1809, and Augustin Cauchy proved the list complete in 1812. These polyhedra are known as collectively as the Kepler-Poinsot polyhedra.

Main article Regular polyhedron - History.

Kepler-Poinsot polyhedra

Small stellated dodecahedron	Great stellated dodecahedron	Great dodecahedron	Great icosahedron

Higher-dimensional polytopes

It was not until the 19th century that a Swiss mathematician, Ludwig Schläfli

Ludwig Schläfli

Ludwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...

, examined and characterised the regular polytopes in higher dimensions. His efforts were first published in full in (Schläfli, 1901), six years posthumously, although parts of it were published in 1855 and 1858 (Schläfli, 1855), (Schläfli, 1858). Interestingly, between 1880 and 1900,
Schläfli's results were rediscovered independently by at least nine
other mathematicians — see (Coxeter, 1948, pp143–144) for more details. Schläfli called such a figure a "polyschem" (in English, "polyscheme" or "polyschema"). The term "polytope" was introduced by Hoppe in 1882, and first used in English by Mrs. Stott

Alicia Boole Stott

Alicia Boole Stott was the third daughter of George Boole and Mary Everest Boole, born in Cork, Ireland. Before marrying Walter Stott, an actuary, in 1890, she was known as Alicia Boole...

some twenty years later. The term "polyhedroids" was also used in earlier literature (Hilbert, 1952).

Coxeter (1948) is probably the most comprehensive printed treatment of Schläfli's and similar results to date. Schläfli showed that there are six regular convex polytopes in 4 dimensions

Convex regular 4-polytope

In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....

, five of these correspond to the Platonic solids and the other one is the 24-cell. There are exactly three in each higher dimension, which correspond to the tetrahedron, cube and octahedron: these are the regular simplices, measure polytopes and cross polytopes. Descriptions of these may be found in the List of regular polytopes. Also of interest are the nonconvex regular 4-polytopes, partially discovered by Schläfli.

By the end of the 19th century, mathematicians such as Arthur Cayley

Arthur Cayley

Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....

and Ludwig Schläfli

Ludwig Schläfli

had developed the theory of regular polytopes in four and higher dimensions, such as the tesseract

Tesseract

and the 24-cell. The latter are hard to visualise, but still retain the aesthetically pleasing symmetry of their lower dimensional cousins. Harder still to imagine are the more modern abstract regular polytopes

Abstract polytope

such as the 57-cell or the 11-cell

11-cell

In mathematics, the 11-cell is a self-dual abstract regular 4-polytope . Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. Its symmetry group is the projective special linear group L2, so it has660 symmetries...

. From the mathematical point of view, however, these objects have the same aesthetic qualities as their more familiar two and three-dimensional relatives.

At the start of the 20th century, the definition of a regular polytope was as follows.

A regular polygon is a polygon whose edges are all equal and whose angles are all equal.
A regular polyhedron is a polyhedron whose faces are all congruent regular polygons, and whose vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

s are all congruent and regular.
And so on, a regular n-polytope is an n-dimensional polytope whose (n − 1)-dimensional faces are all regular and congruent, and whose vertex figures are all regular and congruent.

This is a "recursive" definition. It defines regularity of higher dimensional figures in terms of regular figures of a lower dimension. There is an equivalent (non-recursive) definition, which states that a polytope is regular if it has a sufficient degree of symmetry.

An n-polytope is regular if any set consisting of a vertex, an edge containing it, a 2-dimensional face containing the edge, and so on up to n−1 dimensions, can be mapped to any other such set by a symmetry of the polytope.

So for example, the cube is regular because if we choose a vertex of the cube, and one of the three edges it is on, and one of the two faces containing the edge, then this triplet, or flag, (vertex, edge, face) can be mapped to any other such flag by a suitable symmetry of the cube. Thus we can define a regular polytope very succinctly:

A regular polytope is one which is transitive on its flags.

In the 20th century, some important developments were made. The symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

s of the classical regular polytopes were generalised into what are now called Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

s. Coxeter groups also include the symmetry groups of regular tessellation

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

s of space or of the plane. For example, the symmetry group of an infinite chessboard

Chessboard

A chessboard is the type of checkerboard used in the board game chess, and consists of 64 squares arranged in two alternating colors...

would be the Coxeter group [4,4].

Apeirotopes — infinite polytopes

In the first part of the 20th century, Coxeter and Petrie discovered three infinite structures {4, 6}, {6, 4} and {6, 6}. They called them regular skew polyhedra, because they seemed to satisfy the definition of a regular polyhedron — all the vertices, edges and faces are alike, all the angles are the same, and the figure has no free edges. Nowadays we call them infinite polyhedra or apeirohedra. The regular tilings of the plane {4, 4}, {3, 6} and {6, 3} can also be regarded as infinite polyhedra.

In the 1960s Branko Grünbaum

Branko Grünbaum

Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....

issued a call to the geometric community to consider more abstract types of regular polytopes that he called polystromata. He developed the theory of polystromata, showing examples of new objects he called regular apeirotopes

Apeirogon

An apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...

, that is, regular polytopes with infinitely

Infinity

Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...

many faces. A simple example of an apeirogon

Apeirogon

{∞} would be a zig-zag. It seems to satisfy the definition of a regular polygon — all the edges are the same length, all the angles are the same, and the figure has no loose ends (because they can never be reached). More importantly, perhaps, there are symmetries of the zig-zag that can map any pair of a vertex and attached edge to any other. Since then, other regular apeirogons and higher apeirotopes have continued to be discovered.

Regular complex polytopes

A complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

has a real part, which is the bit we are all familiar with, and an imaginary part, which is a multiple of the square root of minus one. A complex Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

has its x, y, z, etc. coordinates as complex numbers. This effectively doubles the number of dimensions. A polytope constructed in such a unitary space is called a complex polytope
Complex polytope
A complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one....

.

Abstract polytopes

Grünbaum also discovered the 11-cell

11-cell

, a four-dimensional self-dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

object whose facets are not icosahedra, but are "hemi-icosahedra" — that is, they are the shape one gets if one considers opposite faces of the icosahedra to be actually the same face (Grünbaum, 1977). The hemi-icosahedron has only 10 triangular faces, and 6 vertices, unlike the icosahedron, which has 20 and 12.

This concept may be easier for the reader to grasp if one considers the relationship of the cube and the hemicube. An ordinary cube has 8 corners, they could be labeled A to H, with A opposite H, B opposite G, and so on. In a hemicube, A and H would be treated as the same corner. So would B and G, and so on. The edge AB would become the same edge as GH, and the face ABEF would become the same face as CDGH. The new shape has only three faces, 6 edges and 4 corners.

The 11-cell cannot be formed with regular geometry in flat (Euclidean) hyperspace, but only in positively-curved (elliptic) hyperspace.

A few years after Grünbaum's discovery of the 11-cell

11-cell

, H. S. M. Coxeter independently discovered the same shape. He had earlier discovered a similar polytope, the 57-cell (Coxeter 1982, 1984).

By 1994 Grünbaum was considering polytopes abstractly as combinatorial sets of points or vertices, and was unconcerned whether faces were planar. As he and others refined these ideas, such sets came to be called abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...

s. An abstract polytope is defined as a partially ordered set (poset), whose elements are the polytope's faces (vertices, edges, faces etc.) ordered by containment. Certain restrictions are imposed on the set that are similar to properties satisfied by the classical regular polytopes (including the Platonic solids). The restrictions, however, are loose enough that regular tessellations, hemicubes, and even objects as strange as the 11-cell or stranger, are all examples of regular polytopes.

A geometric polytope is understood to be a realization of the abstract polytope, such that there is a one-to-one mapping from the abstract elements to the geometric. Thus, any geometric polytope may be described by the appropriate abstract poset, though not all abstract polytopes have proper geometric realizations.

The theory has since been further developed, largely by Egon Schulte and Peter McMullen (McMullen, 2002), but other researchers have also made contributions.

Regularity of abstract polytopes

Regularity has a related, though different meaning for abstract polytope

Abstract polytope

s, since angles and lengths of edges have no meaning.

The definition of regularity in terms of the transitivity of flags as given in the introduction applies to abstract polytopes.

Any classical regular polytope has an abstract equivalent which is regular, obtained by taking the set of faces. But non-regular classical polytopes can have regular abstract equivalents, since abstract polytopes don't care about angles and edge lengths, for example. And a regular abstract polytope may not be realisable as a classical polytope.

All polygons are regular in the abstract world, for example, whereas only those having equal angles and edges of equal length are regular in the classical world.

Vertex figure of abstract polytopes

The concept of vertex figure is also defined differently for an abstract polytope

Abstract polytope

. The vertex figure of a given abstract n-polytope at a given vertex V is the set of all abstract faces which contain V, including V itself. More formally, it is the abstract section

F_n / V = {F | V ≤ F ≤ F_n}

where F_n is the maximal face, i.e. the notional n-face which contains all other faces. Note that each i-face, i ≥ 0 of the original polytope becomes an (i − 1)-face of the vertex figure.

Unlike the case for Euclidean polytopes, an abstract polytope with regular facets and vertex figures may or may not be regular itself – for example, the square pyramid, all of whose facets and vertex figures are regular abstract polygons.

The classical vertex figure will, however, be a realisation of the abstract one.

Polygons

The traditional way to construct a regular polygon, or indeed any other figure on the plane, is by compass and straightedge

Compass and straightedge

Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....

. Constructing some regular polygons in this way is very simple (the easiest is perhaps the equilateral triangle), some are more complex, and some are impossible ("not constructible"). The simplest few regular polygons that are impossible to construct are the n-sided polygons with n equal to 7, 9, 11, 13, 14, 18, 19, 21,...

Constructibility

Constructible polygon

In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....

in this sense refers only to ideal constructions with ideal tools. Of course reasonably accurate approximations can be constructed by a range of methods; while theoretically possible constructions may be impractical.

Polyhedra

Euclid's Elements gave what amount to ruler-and-compass constructions for the five Platonic solids. (See, for example, Euclid's Elements.) However, the merely practical question of how one might draw a straight line in space, even with a ruler, might lead one to question what exactly it means to "construct" a regular polyhedron. (One could ask the same question about the polygons, of course.)

The English word "construct" has the connotation of systematically building the thing constructed. The most common way presented to construct a regular polyhedron is via a fold-out net

Net (polyhedron)

In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...

. To obtain a fold-out net of a polyhedron, one takes the surface of the polyhedron and cuts it along just enough edges so that the surface may be laid out flat. This gives a plan for the net of the unfolded polyhedron. Since the Platonic solids have only triangles, squares and pentagons for faces, and these are all constructible with a ruler and compass, there exist ruler-and-compass methods for drawing these fold-out nets. The same applies to star polyhedra, although here we must be careful to make the net for only the visible outer surface.

If this net is drawn on cardboard, or similar foldable material (for example, sheet metal), the net may be cut out, folded along the uncut edges, joined along the appropriate cut edges, and so forming the polyhedron for which the net was designed. For a given polyhedron there may be many fold-out nets. For example, there are 11 for the cube, and over 900000 for the dodecahedron. Some interesting fold-out nets of the cube, octahedron, dodecahedron and icosahedron are available here.

Numerous children's toys, generally aimed at the teen or pre-teen age bracket, allow experimentation with regular polygons and polyhedra. For example, klikko provides sets of plastic triangles, squares, pentagons and hexagons that can be joined edge-to-edge in a large number of different ways. A child playing with such a toy could re-discover the Platonic solids (or the Archimedean solid

Archimedean solid

In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...

s), especially if given a little guidance from a knowledgeable adult.

In theory, almost any material may be used to construct regular polyhedra. Instructions for building origami

Origami

is the traditional Japanese art of paper folding, which started in the 17th century AD at the latest and was popularized outside Japan in the mid-1900s. It has since then evolved into a modern art form...

models may be found here, for example. They may be carved out of wood, modeled out of wire, formed from stained glass. The imagination is the limit.

Higher dimensions

In higher dimensions, it becomes harder to say what one means by "constructing" the objects. Clearly, in a 3-dimensional universe, it is impossible to build a physical model of an object having 4 or more dimensions. There are several approaches normally taken to overcome this matter.

The first approach is to embed the higher-dimensional objects in three-dimensional space, using methods analogous to the ways in which three-dimensional objects are drawn on the plane. For example, the fold out nets mentioned in the previous section have higher-dimensional equivalents. Some of these may be viewed at http://www.weimholt.com/andrew/polytope.shtml. One might even imagine building a model of this fold-out net, as one draws a polyhedron's fold-out net on a piece of paper. Sadly, we could never do the necessary folding of the 3-dimensional structure to obtain the 4-dimensional polytope, or polychoron

Polychoron

In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...

, because of the constraints of the physical universe. Another way to "draw" the higher-dimensional shapes in 3 dimensions is via some kind of projection, for example, the analogue of either orthographic

Orthographic projection

Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...

or perspective

Perspective (graphical)

Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...

projection. Coxeter's famous book on polytopes (Coxeter, 1948) has some examples of such orthographic projections. Other examples may be found on the web (see for example http://mathworld.wolfram.com/600-Cell.html). Note that immersing even 4-dimensional polychora directly into two dimensions is quite confusing. Easier to understand are 3-d models of the projections. Such models are occasionally found in science museums or mathematics departments of universities (such as that of the Université Libre de Bruxelles

Université Libre de Bruxelles

The Université libre de Bruxelles is a French-speaking university in Brussels, Belgium. It has 21,000 students, 29% of whom come from abroad, and an equally cosmopolitan staff.-Name:...

).

The intersection of a four (or higher) dimensional regular polytope with a three-dimensional hyperplane will be a polytope (not necessarily regular). If the hyperplane is moved through the shape, the three-dimensional slices can be combined, animated

Animation

Animation is the rapid display of a sequence of images of 2-D or 3-D artwork or model positions in order to create an illusion of movement. The effect is an optical illusion of motion due to the phenomenon of persistence of vision, and can be created and demonstrated in several ways...

into a kind of four dimensional object, where the fourth dimension is taken to be time. In this way, we can see (if not fully grasp) the full four-dimensional structure of the four-dimensional regular polytopes, via such cutaway cross sections. This is analogous to the way a CAT scan reassembles two-dimensional images to form a 3-dimensional representation of the organs being scanned. The ideal would be an animated hologram of some sort, however, even a simple animation such as the one shown can already give some limited insight into the structure of the polytope.

Another way a three-dimensional viewer can comprehend the structure of a four-dimensional polychoron is through being "immersed" in the object, perhaps via some form of virtual reality

Virtual reality

Virtual reality , also known as virtuality, is a term that applies to computer-simulated environments that can simulate physical presence in places in the real world, as well as in imaginary worlds...

technology. To understand how this might work, imagine what one would see if space were filled with cubes. The viewer would be inside one of the cubes, and would be able to see cubes in front of, behind, above, below, to the left and right of himself. If one could travel in these directions, one could explore the array of cubes, and gain an understanding of its geometrical structure. An infinite array of cubes

Cubic honeycomb

The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....

is not a polytope in the traditional sense. In fact, it is a tessellation of 3-dimensional (Euclidean

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

) space. However, a 4-dimensional polychoron can be considered a tessellation of a 3-dimensional non-Euclidean space, namely, a tessellation of the surface of a four-dimensional sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

(a 4-dimensional spherical tiling).

Locally, this space seems like the one we are familiar with, and therefore, a virtual-reality system could, in principle, be programmed to allow exploration of these "tessellations", that is, of the 4-dimensional regular polytopes. The mathematics department at UIUC

University of Illinois at Urbana-Champaign

The University of Illinois at Urbana–Champaign is a large public research-intensive university in the state of Illinois, United States. It is the flagship campus of the University of Illinois system...

has a number of pictures of what one would see if embedded in a tessellation

Tessellation

of hyperbolic space

Hyperbolic space

In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...

with dodecahedra. Such a tessellation forms an example of an infinite abstract regular polytope.

Normally, for abstract regular polytopes, a mathematician considers that the object is "constructed" if the structure of its symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

is known. This is because of an important theorem in the study of abstract regular polytopes, providing a technique that allows the abstract regular polytope to be constructed from its symmetry group in a standard and straightforward manner.

Regular polytopes in nature

For examples of polygons in nature, see:
Each of the Platonic solids occurs naturally in one form or another:
Higher polytopes can obviously not exist in a three-dimensional world. However this might not rule them out altogether. In cosmology

Cosmology

Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...

and in string theory

String theory

String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...

, physicists commonly model the Universe as having many more dimensions. It is possible that the Universe itself has the form of some higher polytope, regular or otherwise. Astronomers have even searched the sky in the last few years, for tell-tale signs of a few regular candidates, so far without definite results.

External links

Stella: Polyhedron Navigator Tool for exploring 3D polyhedra, 4D polytopes, and printing nets
Ernst Haeckel's Kunstformen der Natur online (German)
Interesting fold-out nets of the cube, octahedron, dodecahedron and icosahedron

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.