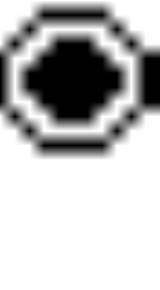
Pentachoron
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. It is also known as the pentachoron, pentatope, or hyperpyramid. It is a 4-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, the simplest possible convex regular 4-polytope
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
(four-dimensional analogue of a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
), and is analogous to the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
in three dimensions and the triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
in two dimensions.
The regular 5-cell is bounded by regular tetrahedra, and is one of the six regular convex polychora, represented by Schläfli symbol {3,3,3}.
Geometry
The 5-cell is self-dual, and its vertex figureVertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a tetrahedron. Its maximal intersection with 3-dimensional space is the triangular prism
Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
. Its dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
is cos−1(1/4), or approximately 75.52°.
Construction
The 5-cell can be constructed from a tetrahedron by adding a 5th vertex such that it is equidistant from all the other vertices of the tetrahedron. (The 5-cell is essentially a 4-dimensional pyramidPyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
with a tetrahedral
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
base.)
The Cartesian coordinates of the vertices of an origin-centered regular 5-cell having edge length 2 are:
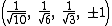
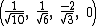
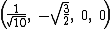
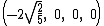
The vertices of a 4-simplex (with edge √2) can be more simply constructed on a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
in 5-space, as permutations of (0,0,0,0,1) or (0,1,1,1,1); in these positions it is a facet of, respectively, the 5-orthoplex or the rectified penteract.
Projections
| Projections to 3 dimensions | |
|---|---|
 Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... wireframe (edge projected onto a 3-sphere 3-sphere In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space... ) |
 A 3D projection of a 5-cell performing a simple rotation |
The vertex-first projection of the pentachoron into 3 dimensions has a tetrahedral Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... projection envelope. The closest vertex of the pentachoron projects to the center of the tetrahedron, as shown here in red. The farthest cell projects onto the tetrahedral envelope itself, while the other 4 cells project onto the 4 flattened tetrahedral regions surrounding the central vertex. |
The edge-first projection of the pentachoron into 3 dimensions has a triangular dipyramidal Triangular dipyramid In geometry, the triangular bipyramid is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.... envelope. The closest edge (shown here in red) projects to the axis of the dipyramid, with the three cells surrounding it projecting to 3 tetrahedral volumes arranged around this axis at 120 degrees to each other. The remaining 2 cells project to the two halves of the dipyramid and are on the far side of the pentatope. |
The face-first projection of the pentachoron into 3 dimensions also has a triangular dipyramidal envelope. The nearest face is shown here in red. The two cells that meet at this face projects to the two halves of the dipyramid. The remaining three cells are on the far side of the pentatope from the 4D viewpoint, and are culled from the image for clarity. They are arranged around the central axis of the dipyramid, just as in the edge-first projection. |
The cell-first projection of the pentachoron into 3 dimensions has a tetrahedral envelope. The nearest cell projects onto the entire envelope, and, from the 4D viewpoint, obscures the other 4 cells; hence, they are not rendered here. |
Alternative names
- Pentachoron
- 4-simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
- Pentatope
- Pentahedroid (Henry Parker Manning)
- Pen (Jonathan Bowers: for pentachoron)
- Hyperpyramid
Related uniform polychora
The pentachoron (5-cell) is the simplest of 9 uniform polychoraUniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
constructed from the [3,3,3] Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
.
Other forms
The 5-cell can also be considered a tetrahedral pyramidPolyhedral pyramid
In 4-dimensional geometry, a polyhedral pyramid is a 4-polytope constructed by a base polyhedron cell and an apex point. The lateral facets are pyramid cells, each constructed by one face of the base polyhedron and the apex....
, constructed as a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
base in a 3-space hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
, and an apex
Apex (geometry)
In geometry, an apex is the vertex which is in some sense the highest of the figure to which it belongs.*In an isosceles triangle, the apex is the vertex where the two sides of equal length meet, opposite the unequal third side....
point above the hyperplane. The four sides of the pyramid are made of tetrahedron cells.
External links
-
- Der 5-Zeller (5-cell) Marco Möller's Regular polytopes in R4 (German)
- Jonathan Bowers, Regular polychora
- Java3D Applets

