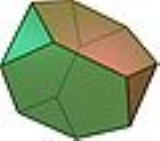
Archimedean solid
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
an Archimedean solid is a highly symmetric, semi-regular convex polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
composed of two or more types of regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s meeting in identical vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. They are distinct from the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s, whose regular polygonal faces do not meet in identical vertices.
"Identical vertices" are usually taken to mean that for any two vertices, there must be an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the entire solid that takes one vertex to the other. Sometimes it is instead only required that the faces that meet at one vertex are related isometrically to the faces that meet at the other. This difference in definitions controls whether the pseudorhombicuboctahedron is considered an Archimedean solid or a Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
.
Prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
and antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s, whose symmetry groups are the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s, are generally not considered to be Archimedean solids, despite meeting the above definition. With this restriction, there are only finitely many Archimedean solids. They can all be made via Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s from the Platonic solids with tetrahedral
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
, octahedral
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
and icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
.
Origin of name
The Archimedean solids take their name from ArchimedesArchimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
, who discussed them in a now-lost work. During the Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
, artist
Artist
An artist is a person engaged in one or more of any of a broad spectrum of activities related to creating art, practicing the arts and/or demonstrating an art. The common usage in both everyday speech and academic discourse is a practitioner in the visual arts only...
s and mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s valued pure forms and rediscovered all of these forms. This search was completed around 1620 by Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, who defined prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
, antiprisms, and the non-convex solids known as the Kepler-Poinsot polyhedra.
Classification
There are 13 Archimedean solids (15 if the mirror imageMirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
s of two enantiomorphs
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
, see below, are counted separately).
Here the vertex configuration refers to the type of regular polygons that meet at any given vertex. For example, a vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
of (4,6,8) means that a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, hexagon, and octagon meet at a vertex (with the order taken to be clockwise around the vertex).
| Name (Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... ) |
Transparent | Solid | Net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... |
Faces | Edges | Vertices | Symmetry group | |
|---|---|---|---|---|---|---|---|---|
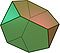
| truncated tetrahedron Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... (3.6.6) |
 |
 |
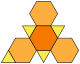 |
8 | 4 triangles 4 hexagons |
18 | 12 | Td |
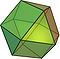
| cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... (3.4.3.4) |
 |
 |
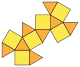 |
14 | 8 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 6 square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s |
24 | 12 | Oh |
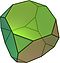
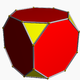
| truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... or truncated hexahedron (3.8.8) |
 |
 |
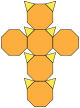 |
14 | 8 triangles 6 octagons |
36 | 24 | Oh |
| truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... (4.6.6) |
 (Animation) |
 |
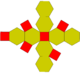 |
14 | 6 squares 8 hexagons |
36 | 24 | Oh |
| rhombicuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... or small rhombicuboctahedron (3.4.4.4 ) |
 |
 |
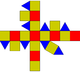 |
26 | 8 triangles 18 squares |
48 | 24 | Oh |
| truncated cuboctahedron Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... or great rhombicuboctahedron (4.6.8) |
 |
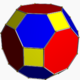 |
 |
26 | 12 squares 8 hexagons 6 octagons |
72 | 48 | Oh |
| snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... or snub hexahedron or snub cuboctahedron (2 chiral Chirality (mathematics) In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object... forms) (3.3.3.3.4) |
 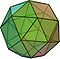 |
 |
 |
38 | 32 triangles 6 squares |
60 | 24 | O |
| icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... (3.5.3.5) |
 |
 |
 |
32 | 20 triangles 12 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s |
60 | 30 | Ih |
| truncated dodecahedron Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... (3.10.10) |
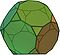 |
 |
 |
32 | 20 triangles 12 decagon Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°... s |
90 | 60 | Ih |
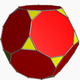
| Truncated icosahedron Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... (5.6.6 ) |
 |
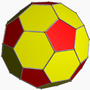 |
 |
32 | 12 pentagons 20 hexagons |
90 | 60 | Ih |
| rhombicosidodecahedron Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... or small rhombicosidodecahedron (3.4.5.4) |
 |
 |
 |
62 | 20 triangles 30 squares 12 pentagons |
120 | 60 | Ih |
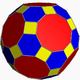
| truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... or great rhombicosidodecahedron (4.6.10) |
 |
 |
 |
62 | 30 squares 20 hexagons 12 decagons |
180 | 120 | Ih |
| snub dodecahedron Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... or snub icosidodecahedron (2 chiral Chirality (mathematics) In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object... forms) (3.3.3.3.5) |
  (Animation) |
 |
 |
92 | 80 triangles 12 pentagons |
150 | 60 | I |
Some definitions of semiregular polyhedron
Semiregular polyhedron
The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
include one more figure, the elongated square gyrobicupola
Elongated square gyrobicupola
In geometry, the elongated square gyrobicupola or pseudorhombicuboctahedron is one of the Johnson solids . The 92 Johnson solids were named and described by Norman Johnson in 1966.- Relation to Rhombicuboctahedron :...
or "pseudo-rhombicuboctahedron".
Properties
The number of vertices is 720° divided by the vertex angle defectDefect (geometry)
In geometry, the defect means the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the plane would...
.
The cuboctahedron and icosidodecahedron are edge-uniform and are called quasi-regular
Quasiregular polyhedron
In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
.
The duals
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the Archimedean solids are called the Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s. Together with the bipyramid
Bipyramid
An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
s and trapezohedra
Trapezohedron
The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...
, these are the face-uniform solids with regular vertices.
Chirality
The snub cube and snub dodecahedron are known as chiralChirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
, as they come in a left-handed (Latin: levomorph or laevomorph) form and right-handed (Latin: dextromorph) form. When something comes in multiple forms which are each other's three-dimensional mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
, these forms may be called enantiomorphs. (This nomenclature is also used for the forms of certain chemical compound
Chemical compound
A chemical compound is a pure chemical substance consisting of two or more different chemical elements that can be separated into simpler substances by chemical reactions. Chemical compounds have a unique and defined chemical structure; they consist of a fixed ratio of atoms that are held together...
s).
See also
- Aperiodic tilingAperiodic tilingAn aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
- Catalan solidCatalan solidIn mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
- List of uniform polyhedra
- Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
- QuasicrystalQuasicrystalA quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
- semiregular polyhedronSemiregular polyhedronThe term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
- uniform polyhedronUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
External links
- Archemedian Solids by Eric W. WeissteinEric W. WeissteinEric W. Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science . He currently works for Wolfram Research, Inc.-Education:...
, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Paper models of Archimedean Solids and Catalan Solids
- Free paper models(nets) of Archimedean solids
- The Uniform Polyhedra by Dr. R. Mäder
- Virtual Reality Polyhedra, The Encyclopedia of Polyhedra by George W. Hart
- Penultimate Modular Origami by James S. Plank
- Interactive 3D polyhedra in Java
- Stella: Polyhedron Navigator: Software used to create many of the images on this page.
- Paper Models of Archimedean (and other) Polyhedra

