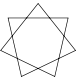
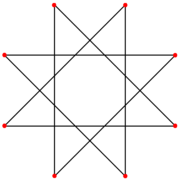
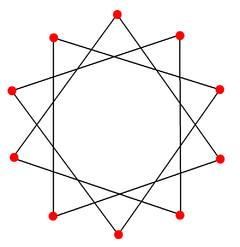
Star polygon
Encyclopedia
EWLINE
|
||||||||
| Schläfli symbol 2<2q Greatest common divisor In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to... (p,q)=1 |
{p/q} | |||||||
|---|---|---|---|---|---|---|---|---|
| Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:... and Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects.... |
p | |||||||
| Coxeter–Dynkin diagram | ||||||||
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Dihedral (Dp) | |||||||
| Dual polygon Dual polygon In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.-Properties:Regular polygons are self-dual.... |
Self-dual | |||||||
| Internal angle Internal angle In geometry, an interior angle is an angle formed by two sides of a polygon that share an endpoint. For a simple, convex or concave polygon, this angle will be an angle on the 'inner side' of the polygon... (degree Degree (angle) A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians... s) |
 |
A star polygon is a non-convex polygon which looks in some way like a star. Only the regular ones have been studied in any depth; star polygons in general appear not to have been formally defined. They should not be confused with star domain
Star domain
In mathematics, a set S in the Euclidean space Rn is called a star domain if there exists x_0 in S such that for all x in S the line segment from x_0 to x is in S...
s.
Regular star polygons
In geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a regular star polygon is a self-intersecting, equilateral equiangular polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, created by connecting one vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of a simple, regular, p-sided polygon to another, non-adjacent vertex and continuing the process until the original vertex is reached again. Alternatively for integers p and q, it can be considered as being constructed by connecting every qth point out of p points regularly spaced in a circular placement. For instance, in a regular pentagon, a five-pointed star can be obtained by drawing a line from the first to the third vertex, from the third vertex to the fifth vertex, from the fifth vertex to the second vertex, from the second vertex to the fourth vertex, and from the fourth vertex to the first vertex. The notation for such a polygon is {p/q} (see Schläfli symbol), which is equal to {p/p-q}. Regular star polygons will be produced when p and q are relatively prime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
(they share no factors). A regular star polygon can also be represented as a sequence of stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
s of a convex regular core polygon. Regular star polygons were first studied systematically by Thomas Bradwardine
Thomas Bradwardine
Thomas Bradwardine was an English scholar, scientist, courtier and, very briefly, Archbishop of Canterbury. As a celebrated scholastic philosopher and doctor of theology, he is often called Doctor Profundus, .-Life:He was born either at Hartfield in Sussex or at Chichester, where his family were...
.
Examples
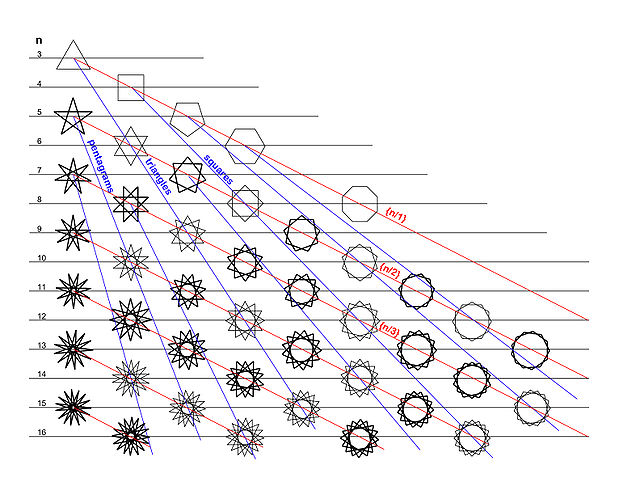 |
Star figures

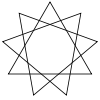
Degeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
star polygon.
In other cases where n and m have a common factor, a star polygon for a lower n is obtained, and rotated versions can be combined. These figures are called star figures or improper star polygons or compound polygons. The same notation {n/m} is often used for them, although authorities such as Grünbaum (1994) regard (with some justification) the form k{n} as being more correct, where usually k=m.
A further complication comes when we compound two or more star polygons, as for example two pentagrams, differing by a rotation of 36°, inscribed in a decagon. This is correctly written in the form k{n/m}, as 2{5/2}, rather than the commonly-used {10/4}.
A six-pointed star, like a hexagon, can be created using a compass and a straight edge:
- Make a circle of any size with the compass.
- Without changing the radius of the compass, set its pivot on the circle's circumference, and find one of the two points where a new circle would intersect the first circle.
- With the pivot on the last point found, similarly find a third point on the circumference, and repeat until six such points have been marked.
- With a straight edge, join alternate points on the circumference to form two overlapping equilateral triangles.
Symmetry
Regular star polygons and star figures can be thought of as diagramming cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s
 of the finite group
of the finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
 .
.The symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of {n/k} is dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dn of order 2n, independent of k.
Irregular star polygons

Vertex
Vertex may refer to:-Mathematics:*Vertex , an angle point of any shape or angle*Vertex , a node in a graph*Vertex , a local extreme point of curvature...
figures for the uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
, defined by the sequence of regular polygon faces around each vertex, allowing for both multiple turns, and retrograde directions. (See vertex figures at List of uniform polyhedra)
The unicursal hexagram
Unicursal Hexagram
The unicursal hexagram is a hexagram or six-pointed star that can be traced or drawn unicursally, in one continuous line rather than by two overlaid triangles...
is another example of a cyclic irregular star polygon, containing only D2h Dihedral symmetry.
Interiors of star polygons
Star polygons leave an ambiguity of interpretation for interiors. This diagram demonstrates three interpretations of a pentagram.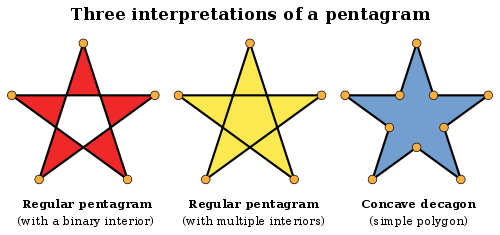
- The left-hand interpretation has the 5 vertices of a regular pentagon connected alternately on a cyclic path, skipping alternate vertices. The interior is everything immediately left (or right) from each edge (until the next intersection). This makes the core convex pentagonal region actually "outside", and in general you can determine inside by a binary even-odd ruleEven-odd ruleThe even–odd rule is an algorithm implemented in vector-based graphic software, like the PostScript language, which determines how a graphical shape with more than one closed outline will be filled...
of counting how many edges are intersected from a point along a ray to infinity. - The middle interpretation also has the 5 vertices of a regular pentagon connected alternately on a cyclic path. The interior may be treated either:
- as the inside of a simple 10-sided polygon perimeter boundary, as below.
- with the central convex pentagonal region surrounded twice, because the starry perimeter winds round it twice.
- The right-hand interpretation creates new vertices at the intersections of the edges (5 in this case) and defines a new concave decagon (10-pointed polygon) formed by perimeter path of the middle interpretation; it is in fact no longer a pentagram.
What is the area inside the pentagram? Each interpretation leads to a different answer.
Example interpretations of a star prism
{7/2} heptagrammic prism: Heptagrams with 2-sided interior |
 Heptagrams with a simple perimeter interior |
The heptagrammic prism above shows different interpretations can create very different appearances.
Builders of polyhedron model
Polyhedron model
A polyhedron model is a physical construction of a polyhedron, constructed from cardboard, plastic board, wood board or other panel material, or, less commonly, solid material....
s, like Magnus Wenninger, usually represent star polygon faces in the concave form, without internal edges shown.
Star polygons in art and culture
Star polygons feature prominently in art and culture. Such polygons are may or may not be regularRegular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
but they are always highly symmetrical
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. Examples include:
- The {5/2} star pentagon is also known as a pentagramPentagramA pentagram is the shape of a five-pointed star drawn with five straight strokes...
, pentalpha or pentangle, and historically has been considered by many magicMagic (paranormal)Magic is the claimed art of manipulating aspects of reality either by supernatural means or through knowledge of occult laws unknown to science. It is in contrast to science, in that science does not accept anything not subject to either direct or indirect observation, and subject to logical...
al and religiousReligionReligion is a collection of cultural systems, belief systems, and worldviews that establishes symbols that relate humanity to spirituality and, sometimes, to moral values. Many religions have narratives, symbols, traditions and sacred histories that are intended to give meaning to life or to...
cults to have occultOccultThe word occult comes from the Latin word occultus , referring to "knowledge of the hidden". In the medical sense it is used to refer to a structure or process that is hidden, e.g...
significance. - The simplest non-degenerate complex star polygon which is two {6/2} polygons (i.e., triangles), the hexagram (Star of DavidStar of DavidThe Star of David, known in Hebrew as the Shield of David or Magen David is a generally recognized symbol of Jewish identity and Judaism.Its shape is that of a hexagram, the compound of two equilateral triangles...
, Seal of SolomonSeal of SolomonIn Medieval Jewish, Christian and Islamic legends, the Seal of Solomon was a magical signet ring said to have been possessed by King Solomon, which variously gave him the power to command demons, genies , or to speak with animals.-In legend :...
). - The {7/3} and {7/2} star polygons which are known as heptagramHeptagramA heptagram or septegram is a seven-pointed star drawn with seven straight strokes.- Geometry :In general, a heptagram is any self-intersecting heptagon ....
s and also have occult significance, particularly in the KabbalahKabbalahKabbalah/Kabala is a discipline and school of thought concerned with the esoteric aspect of Rabbinic Judaism. It was systematized in 11th-13th century Hachmei Provence and Spain, and again after the Expulsion from Spain, in 16th century Ottoman Palestine...
and in WiccaWiccaWicca , is a modern Pagan religious movement. Developing in England in the first half of the 20th century, Wicca was popularised in the 1950s and early 1960s by a Wiccan High Priest named Gerald Gardner, who at the time called it the "witch cult" and "witchcraft," and its adherents "the Wica."...
. - The complex {8/2} star polygon (i.e. two squares), which is known as the Star of Lakshmi and figures in HinduismHinduismHinduism is the predominant and indigenous religious tradition of the Indian Subcontinent. Hinduism is known to its followers as , amongst many other expressions...
; - The {8/3} star polygon (octagram), and the complex star polygon of two {16/6} polygons, which are frequent geometrical motifs in MughalMughal EmpireThe Mughal Empire , or Mogul Empire in traditional English usage, was an imperial power from the Indian Subcontinent. The Mughal emperors were descendants of the Timurids...
Islamic art and architectureIslamic architectureIslamic architecture encompasses a wide range of both secular and religious styles from the foundation of Islam to the present day, influencing the design and construction of buildings and structures in Islamic culture....
; the first is on the coat of arms of Azerbaijan. - An eleven pointed star called the hendecagram, which apparently was used on the tomb of Shah Nemat Ollah Vali.
Some symbols based on a star polygon have interlacing, by small gaps, and/or, in the case of a star figure, using different colors.
 |
.svg.png) |
See also
- Complex polygonComplex polygonThe term complex polygon can mean two different things:*In computer graphics, as a polygon which is neither convex nor concave.*In geometry, as a polygon in the unitary plane, which has two complex dimensions.-Computer graphics:...
- List of regular polytopes - Nonconvex forms (2D)
- Magic star
- Star polyhedronStar polyhedronIn geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
- Star polychoron (4-polytopes)
- Star-shaped polygonStar-shaped polygonA star-shaped polygon is a polygonal region in the plane which is a star domain, i.e., a polygon P is star-shaped, if there exists a point z such that for each point p of P the segment zp lies entirely within P.The set of all points z with the described property is called the kernel of...
- Stellation#Stellated polygons