
Vertex figure
Encyclopedia


Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
or polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
is sliced off.
Definitions - theme and variations
Take some vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure.More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
, or space-filling tessellation
Honeycomb
A honeycomb is a mass of hexagonal waxcells built by honey bees in their nests to contain their larvae and stores of honey and pollen.Beekeepers may remove the entire honeycomb to harvest honey...
with polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
.
As a flat slice
Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. This is perhaps the commonest approach, and the most easily understood. Different authors make the slice in different places. Wenninger (2003) cuts each edge a unit distance from the vertex. For uniform polyhedra the Dorman Luke construction cuts each connected edge at its mid-point. Other authors make the cut through the vertex at the other end of each edge.As a spherical polygon
Cromwell (1999) makes a spherical cut or scoop, centered on the vertex. The cut surface or vertex figure is thus a spherical polygon marked on this sphere.As the set of connected vertices
Many combinatorial and computational approaches (e.g. Skilling, 1975) treat a vertex figure as the ordered (or partially ordered) set of points of all the neighboring (connected via an edge) vertices to the given vertex.Abstract definition
In the theory of abstract polytopeAbstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s, the vertex figure at a given vertex V comprises all the elements which are incident on the vertex; edges, faces, etc. More formally it is the (n−1)-section Fn/V, where Fn is the greatest face.
This set of elements is elsewhere known as a vertex star.
General properties
A vertex figure for an n-polytope is an (n-1)-polytope. For example, a vertex figure for a polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
is a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
figure, and the vertex figure for a polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
figure.
By considering the connectivity of these neighboring vertices an (n-1)-polytope, the vertex figure, can be constructed for each vertex of a polytope:
- Each vertexVertex (geometry)In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of the vertex figure coincides with a vertex of the original polytope. - Each edgeGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
of the vertex figure exists on or inside of a face of the original polytope connecting two alternate vertices from an original face. - Each faceFace (geometry)In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
of the vertex figure exists on or inside a cell of the original n-polytope (for n>3). - ...and so on to higher order elements in higher order polytopes.
Vertex figures are the most useful for uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s because one vertex figure can imply the entire polytope.
For polyhedra, the vertex figure can be represented by a vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
notation, by listing the faces in sequence around a vertex. For example 3.4.4.4 is a vertex with one triangle and 3 squares, and it represents the rhombicuboctahedron
Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
.
If the polytope is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
, the vertex figure will exist in a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
surface of the n-space. In general the vertex figure need not be planar.
Also nonconvex polyhedra, the vertex figure may also be nonconvex. Uniform polytopes can have either star polygon faces and vertex figures for instance.
Dorman Luke construction
For a uniform polyhedron, the face of the dual polyhedronDual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
may be found from the original polyhedron's vertex figure using the Dorman Luke construction.
Regular polytopes
If a polytope is regular, it can be represented by a Schläfli symbol and both the cellCell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
and the vertex figure can be trivially extracted from this notation.
In general a regular polytope with Schläfli symbol {a,b,c,....,y,z} has cells as {a,b,c,...,y}, and vertex figures as {b,c,...,y,z}.
- For a regular polyhedronPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
{p,q}, the vertex figure is {q}, a q-gon.- Example, the vertex figure for a cube {4,3}, is the triangle {3}.
- For a regular polychoronPolychoronIn geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
or space-filling tessellationHoneycomb (geometry)In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
{p,q,r}, the vertex figure is {q,r}.- Example, the vertex figure for a hypercube {4,3,3}, the vertex figure is a regular tetrahedron {3,3}.
- Also the vertex figure for a cubic honeycombCubic honeycombThe cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
{4,3,4}, the vertex figure is a regular octahedron {3,4}.
Since the dual polytope of a regular polytope is also regular and represented by the Schläfli symbol indices reversed, it is easy to see the dual of the vertex figure is the cell of the dual polytope. For regular polyhedra, this is a special case of the Dorman Luke construction
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
.
An example vertex figure of a honeycomb

Truncated cubic honeycomb
The truncated cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of truncated cubes and octahedra in a ratio of 1:1.- Symmetry :...
is a nonuniform square pyramid
Square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
. One octahedron and four truncated cube meet at each vertex for form a space-filling tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
.
| Vertex figure: A nonuniform square pyramid Square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :... |
 Schlegel diagram |
Perspective |
| Created as a square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... base from an octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 (3.3.3.3) |
| And four isosceles triangle sides from truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... s |
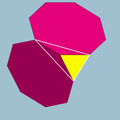 (3.8.8) |
Edge figure

An edge figure will be a (n-2)-polytope, representing the arrangement of facets around a given edge. Regular and single-ringed uniform polytopes will have a single edge figure type, while in general, a uniform polytope can have as many edges as active mirrors in the construction, since each active mirror produces one edge in the fundamental domain.
Regular polytopes (and honeycombs) have a single edge figure which is also regular. For a regular polytope {p,q,r,s,...,z}, the edge figure is {r,s,...,z}.
In four dimensions, the edge figure of a 4-polytope or 3-honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
is a polygon representing the arrangement of a set of facets around an edge. For example, the edge figure for a regular cubic honeycomb
Cubic honeycomb
The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
{4,3,4} is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, and for a regular polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
{p,q,r} is the polygon {r}.
Less trivially, the truncated cubic honeycomb
Truncated cubic honeycomb
The truncated cubic honeycomb is a uniform space-filling tessellation in Euclidean 3-space. It is composed of truncated cubes and octahedra in a ratio of 1:1.- Symmetry :...
t0,1{4,3,4}, has a square pyramid
Square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
vertex figure, with truncated cube
Truncated cube
In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
and octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
cells. Here there are 2 types of edge figures. One is a square edge figure at the apex of the pyramid. This represents the four truncated cubes around an edge. The other four edge figures are isosceles triangle on the base vertices of the pyramid. These represent the arrangement of two truncated cubes and one octahedron around the other edges.

