Tesseract
Encyclopedia
In geometry
, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube
. The tesseract is to the cube as the cube is to the square
. Just as the surface of the cube consists of 6 square faces
, the hypersurface of the tesseract consists of 8 cubical cells
. The tesseract is one of the six convex regular 4-polytope
s.
A generalization of the cube to dimensions greater than three is called a "hypercube
", "n-cube" or "measure polytope
". The tesseract is the four-dimensional hypercube, or 4-cube.
According to the Oxford English Dictionary, the word tesseract was coined and first used in 1888 by Charles Howard Hinton
in his book A New Era of Thought
, from the Greek
("four rays"), referring to the four lines from each vertex to other vertices. Some people have called the same figure a tetracube, and also simply a hypercube (although the term hypercube is also used with dimensions greater than 4).
with three cube
s folded together around every edge, it has Schläfli symbol {4,3,3}. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3} × { }. As a duoprism
, a Cartesian product
of two squares
, it can be named by a composite Schläfli symbol {4}×{4}.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure
of the tesseract is a regular tetrahedron
. The dual polytope of the tesseract is called the hexadecachoron, or 16-cell, with Schläfli symbol {3,3,4}.
The standard tesseract in Euclidean 4-space
is given as the convex hull
of the points (±1, ±1, ±1, ±1). That is, it consists of the points:
A tesseract is bounded by eight hyperplane
s (xi = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
The construction of a hypercube can be imagined the following way:
This structure is not easily imagined but it is possible to project tesseracts into three- or two-dimensional spaces. Furthermore, projections on the 2D-plane become more instructive by rearranging the positions of the projected vertices. In this fashion, one can obtain pictures that no longer reflect the spatial relationships within the tesseract, but which illustrate the connection structure of the vertices, such as in the following examples:
A tesseract is in principle obtained by combining two cubes. The scheme is similar to the construction of a cube from two squares: juxtapose two copies of the lower dimensional cube and connect the corresponding vertices. Each edge of a tesseract is of the same length. This view is of interest when using tesseracts as the basis for a network topology
to link multiple processors in parallel computing
: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
Tesseracts are also bipartite graph
s, just as a path, square, cube and tree are.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
. The tesseract is to the cube as the cube is to the square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
. Just as the surface of the cube consists of 6 square faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, the hypersurface of the tesseract consists of 8 cubical cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
. The tesseract is one of the six convex regular 4-polytope
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
s.
A generalization of the cube to dimensions greater than three is called a "hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
", "n-cube" or "measure polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
". The tesseract is the four-dimensional hypercube, or 4-cube.
According to the Oxford English Dictionary, the word tesseract was coined and first used in 1888 by Charles Howard Hinton
Charles Howard Hinton
Charles Howard Hinton was a British mathematician and writer of science fiction works titled Scientific Romances. He was interested in higher dimensions, particularly the fourth dimension, and is known for coining the word tesseract and for his work on methods of visualising the geometry of...
in his book A New Era of Thought
A New Era of Thought
A New Era of Thought is a non-fiction work written by Charles Howard Hinton, was published in 1888 and reprinted in 1900 by Swan Sonnenschein & Co. Ltd., London. A New Era of Thought is about the fourth dimension and its implications on human thinking. It influenced the work of P.D. Ouspensky,...
, from the Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
("four rays"), referring to the four lines from each vertex to other vertices. Some people have called the same figure a tetracube, and also simply a hypercube (although the term hypercube is also used with dimensions greater than 4).
Geometry
The tesseract can be constructed in a number of ways. As a regular polytopeRegular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
with three cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s folded together around every edge, it has Schläfli symbol {4,3,3}. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3} × { }. As a duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
, a Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two squares
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, it can be named by a composite Schläfli symbol {4}×{4}.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
of the tesseract is a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. The dual polytope of the tesseract is called the hexadecachoron, or 16-cell, with Schläfli symbol {3,3,4}.
The standard tesseract in Euclidean 4-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is given as the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the points (±1, ±1, ±1, ±1). That is, it consists of the points:
A tesseract is bounded by eight hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s (xi = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
Projections to 2 dimensions
- 1-dimensional: Two points A and B can be connected to a line, giving a new line segment AB.
- 2-dimensional: Two parallel line segments AB and CD can be connected to become a square, with the corners marked as ABCD.
- 3-dimensional: Two parallel squares ABCD and EFGH can be connected to become a cube, with the corners marked as ABCDEFGH.
- 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to become a hypercube, with the corners marked as ABCDEFGHIJKLMNOP.
A tesseract is in principle obtained by combining two cubes. The scheme is similar to the construction of a cube from two squares: juxtapose two copies of the lower dimensional cube and connect the corresponding vertices. Each edge of a tesseract is of the same length. This view is of interest when using tesseracts as the basis for a network topology
Network topology
Network topology is the layout pattern of interconnections of the various elements of a computer or biological network....
to link multiple processors in parallel computing
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
Tesseracts are also bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s, just as a path, square, cube and tree are.
Parallel projections to 3 dimensions
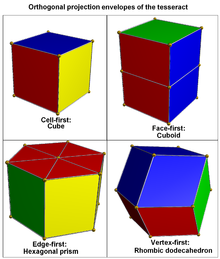 Graphical projection Graphical projection is a protocol by which an image of a three-dimensional object is projected onto a planar surface without the aid of mathematical calculation, used in technical drawing.- Overview :... of the tesseract into 3-dimensional space has a cubical Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... envelope. The nearest and farthest cells are projected onto the cube, and the remaining 6 cells are projected onto the 6 square faces of the cube. The face-first parallel projection of the tesseract into 3-dimensional space has a cuboid Cuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... al envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the 4 remaining cells project to the side faces. The edge-first parallel projection of the tesseract into 3-dimensional space has an envelope in the shape of a hexagonal prism Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... . Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto 6 rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases. The vertex-first parallel projection of the tesseract into 3-dimensional space has a rhombic dodecahedral Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... envelope. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepiped Parallelepiped In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts... s, giving a total of 8 possible parallelepipeds. The images of the tesseract's cells under this projection are precisely these 8 parallelepipeds. This projection is also the one with maximal volume. |
Image gallery
 Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... . There are 261 distinct nets of the tesseract. The unfoldings of the tesseract can be counted by mapping the nets to paired trees (a tree Tree (graph theory) In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree... together with a perfect matching in its complement Complement graph In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and... ). |
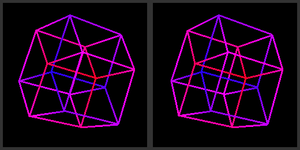 A stereoscopic Stereogram A stereogram is pair of two-dimensional panels depicting the view of a scene or an object from the vantage points of the right and left eyes. Observing the panels superimposed in a stereoscope results in the experience of three-dimensionality by virtue of the fact that object depth is encoded as... 3D projection of a tesseract. |
Perspective projections
 A 3D projection of an 8-cell performing a simple rotation about a plane which bisects the figure from front-left to back-right and top to bottom |
 A 3D projection of an 8-cell performing a double rotation about two orthogonal planes |
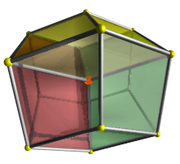 Perspective with hidden volume elimination. The red corner is the nearest in 4D and has 4 cubical cells meeting around it. |
The tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... forms the convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... of the tesseract's vertex-centered central projection. Four of 8 cubic cells are shown. The 16th vertex is projected to infinity and the four edges to it are not shown. |
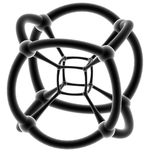 Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... (Edges are projected onto the 3-sphere 3-sphere In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space... ) |
See also
- Four-dimensional space
- 3-sphere3-sphereIn mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
- Ludwig SchläfliLudwig SchläfliLudwig Schläfli was a Swiss geometer and complex analyst who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction...
- Polytopes - Grande ArcheGrande ArcheLa Grande Arche de la Défense is a monument and building in the business district of La Défense and in the commune of Puteaux, to the west of Paris, France...
- a monument and building in the business district of La DéfenseLa DéfenseLa Défense is a major business district of the Paris aire urbaine. With a population of 20,000, it is centered in an orbital motorway straddling the Hauts-de-Seine département municipalities of Nanterre, Courbevoie and Puteaux... - A Wrinkle in TimeA Wrinkle in TimeA Wrinkle in Time is a science fantasy novel by Madeleine L'Engle, first published in 1962. The story revolves around a young girl whose father, a government scientist, has gone missing after working on a mysterious project called a tesseract. The book won a Newbery Medal, Sequoyah Book Award, and...
- a science fantasy novel using the word tesseract
External links
-
- The Tesseract Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
- Der 8-Zeller (8-cell) Marco Möller's Regular polytopes in R4 (German)
- WikiChoron: Tesseract
- HyperSolids is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
- Hypercube 98 via the Internet archive A WindowsMicrosoft WindowsMicrosoft Windows is a series of operating systems produced by Microsoft.Microsoft introduced an operating environment named Windows on November 20, 1985 as an add-on to MS-DOS in response to the growing interest in graphical user interfaces . Microsoft Windows came to dominate the world's personal...
program that displays animated hypercubes, by Rudy RuckerRudy RuckerRudolf von Bitter Rucker is an American mathematician, computer scientist, science fiction author, and philosopher, and is one of the founders of the cyberpunk literary movement. The author of both fiction and non-fiction, he is best known for the novels in the Ware Tetralogy, the first two of... - ken perlin's home page A way to visualize hypercubes, by Ken PerlinKen PerlinKen Perlin is a professor in the Department of Computer Science at New York University, founding director of the Media Research Lab at NYU, and the Director of the Games for Learning Institute. His research interests include graphics, animation, multimedia, and science education...
- Some Notes on the Fourth Dimension includes very good animated tutorials on several different aspects of the tesseract, by Davide P. Cervone
- Tesseract animation with hidden volume elimination