
Game theory
Encyclopedia
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others. More formally, it is "the study of mathematical model
s of conflict and cooperation between intelligent rational
decision-makers." An alternative term suggested "as a more descriptive name for the discipline" is interactive decision theory
. Game theory is mainly used in economics, political science, and psychology, and other, more prescribed sciences, like logic or biology. The subject first addressed zero-sum games, such that one person's gains exactly equal net losses of the other participant(s). Today, however, game theory applies to a wide range of class relations, and has developed into an umbrella term
for the logical side of science, to include both human and non-humans, like computers. Classic uses include a sense of balance in numerous games, where each person has found or developed a tactic that cannot successfully better his results, given the other approach.
Mathematical game theory had beginnings with some publications by Émile Borel, which led to his book Applications aux Jeux de Hasard. However, his results were limited, and the theory regarding the non-existence of blended-strategy equilibrium in two-player games was incorrect. Modern game theory began with the idea regarding the existence of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann
. Von Neumann's original proof used Brouwer's fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was followed by his 1944 book Theory of Games and Economic Behavior
, with Oskar Morgenstern
, which considered cooperative games of several players. The second edition of this book provided an axiomatic theory of expected utility, which allowed mathematical statisticians and economists to treat decision-making under uncertainty.
This theory was developed extensively in the 1950s by many scholars. Game theory was later explicitly applied to biology in the 1970s, although similar developments go back at least as far as the 1930s. Game theory has been widely recognized as an important tool in many fields. Eight game-theorists have won the Nobel Memorial Prize in Economic Sciences
, and John Maynard Smith
was awarded the Crafoord Prize
for his application of game theory to biology.
 Early discussions of examples of two-person games occurred long before the rise of modern, mathematical game theory. The first known discussion of game theory occurred in a letter written by James Waldegrave
Early discussions of examples of two-person games occurred long before the rise of modern, mathematical game theory. The first known discussion of game theory occurred in a letter written by James Waldegrave
in 1713. In this letter, Waldegrave provides a minimax
mixed strategy solution to a two-person version of the card game le Her
. James Madison
made what we now recognize as a game-theoretic analysis of the ways states can be expected to behave under different systems of taxation. In his 1838 Recherches sur les principes mathématiques de la théorie des richesses (Researches into the Mathematical Principles of the Theory of Wealth), Antoine Augustin Cournot
considered a duopoly
and presents a solution that is a restricted version of the Nash equilibrium
.
The Danish mathematician Zeuthen proved that a mathematical model has a winning strategy by using Brouwer's fixed point theorem
. In his 1938 book Applications aux Jeux de Hasard and earlier notes, Émile Borel
1938 book proved a minimax theorem for two-person zero-sum matrix games only when the pay-off matrix was symmetric. Borel conjectured that non-existence of a mixed-strategy equilibria in two-person zero-sum games would occur, a conjecture that was proved false.
Game theory did not really exist as a unique field until John von Neumann
published a paper in 1928. Von Neumann's original proof used Brouwer's fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics
. His paper was followed by his 1944 book Theory of Games and Economic Behavior
, with Oskar Morgenstern
, which considered cooperative games of several players. The second edition of this book provided an axiomatic theory of expected utility, which allowed mathematical statisticians and economists to treat decision-making under uncertainty. Von Neumann's work in game theory culminated in the 1944 book Theory of Games and Economic Behavior
by von Neumann and Oskar Morgenstern
. This foundational work contains the method for finding mutually consistent solutions for two-person zero-sum games. During this time period, work on game theory was primarily focused on cooperative game
theory, which analyzes optimal strategies for groups of individuals, presuming that they can enforce agreements between them about proper strategies.
In 1950, the first discussion of the prisoner's dilemma
appeared, and an experiment was undertaken on this game at the RAND corporation. Around this same time, John Nash
developed a criterion for mutual consistency of players' strategies, known as Nash equilibrium, applicable to a wider variety of games than the criterion proposed by von Neumann and Morgenstern. This equilibrium is sufficiently general to allow for the analysis of non-cooperative game
s in addition to cooperative ones.
Game theory experienced a flurry of activity in the 1950s, during which time the concepts of the core
, the extensive form game
, fictitious play
, repeated game
s, and the Shapley value
were developed. In addition, the first applications of Game theory to philosophy
and political science
occurred during this time.
In 1965, Reinhard Selten
introduced his solution concept
of subgame perfect equilibria
, which further refined the Nash equilibrium (later he would introduce trembling hand perfection as well). In 1967, John Harsanyi
developed the concepts of complete information
and Bayesian game
s. Nash, Selten and Harsanyi became Economics Nobel Laureates
in 1994 for their contributions to economic game theory.
In the 1970s, game theory was extensively applied in biology
, largely as a result of the work of John Maynard Smith
and his evolutionarily stable strategy
. In addition, the concepts of correlated equilibrium
, trembling hand perfection, and common knowledge
were introduced and analyzed.
In 2005, game theorists Thomas Schelling
and Robert Aumann followed Nash, Selten and Harsanyi as Nobel Laureates. Schelling worked on dynamic models, early examples of evolutionary game theory
. Aumann contributed more to the equilibrium school, introducing an equilibrium coarsening, correlated equilibrium, and developing an extensive formal analysis of the assumption of common knowledge and of its consequences.
In 2007, Leonid Hurwicz
, together with Eric Maskin
and Roger Myerson
, was awarded the Nobel Prize in Economics "for having laid the foundations of mechanism design
theory." Myerson's contributions include the notion of proper equilibrium
, and an important graduate text: Game Theory, Analysis of Conflict . Hurwicz introduced and formalized the concept of incentive compatibility
.
s, a set of moves (or strategies
) available to those players, and a specification of payoffs for each combination of strategies. Most cooperative games are presented in the characteristic function form, while the extensive and the normal forms are used to define noncooperative games.
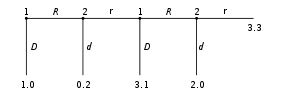
 The extensive form can be used to formalize games with a time sequencing of moves. Games here are played on trees
The extensive form can be used to formalize games with a time sequencing of moves. Games here are played on trees
(as pictured to the left). Here each vertex
(or node) represents a point of choice for a player. The player is specified by a number listed by the vertex. The lines out of the vertex represent a possible action for that player. The payoffs are specified at the bottom of the tree. The extensive form can be viewed as a multi-player generalization of a decision tree
.
In the game pictured to the left, there are two players. Player 1 moves first and chooses either F or U. Player 2 sees Player 1s move and then chooses A or R. Suppose that Player 1 chooses U and then Player 2 chooses A, then Player 1 gets 8 and Player 2 gets 2.
The extensive form can also capture simultaneous-move games and games with imperfect information. To represent it, either a dotted line connects different vertices to represent them as being part of the same information set (i.e., the players do not know at which point they are), or a closed line is drawn around them. (See example in the imperfect information section.)
which shows the players, strategies, and payoffs (see the example to the right). More generally it can be represented by any function that associates a payoff for each player with every possible combination of actions. In the accompanying example there are two players; one chooses the row and the other chooses the column. Each player has two strategies, which are specified by the number of rows and the number of columns. The payoffs are provided in the interior. The first number is the payoff received by the row player (Player 1 in our example); the second is the payoff for the column player (Player 2 in our example). Suppose that Player 1 plays Up and that Player 2 plays Left. Then Player 1 gets a payoff of 4, and Player 2 gets 3.
When a game is presented in normal form, it is presumed that each player acts simultaneously or, at least, without knowing the actions of the other. If players have some information about the choices of other players, the game is usually presented in extensive form.
Every extensive-form game has an equivalent normal-form game, however the transformation to normal form may result in an exponential blowup in the size of the representation, making it computationally impractical.
The origin of this form is to be found in John von Neumann and Oskar Morgenstern's book; when looking at these instances, they guessed that when a union C appears, it works against the fraction (N/C) as if two individuals were playing a normal game. The balanced payoff of C is a basic function. Although there are differing examples that help determine coalitional amounts from normal games, not all appear that in their function form can be derived from such.
Formally, a characteristic function is seen as: (N,v), where N represents the group of people and v:2^N-->R is a normal utility.
Such characteristic functions have expanded to describe games where there is no removable utility.
of coalition formation. In the partition function form the payoff of a coalition depends not only on its members, but also on the way the rest of the players are partitioned .
, game theory has been used to study a wide variety of human and animal behaviors. It was initially developed in economics
to understand a large collection of economic behaviors, including behaviors of firms, markets, and consumers. The use of game theory in the social sciences has expanded, and game theory has been applied to political, sociological, and psychological behaviors as well.
Game-theoretic analysis was initially used to study animal behavior by Ronald Fisher
in the 1930s (although even Charles Darwin
makes a few informal game-theoretic statements). This work predates the name "game theory", but it shares many important features with this field. The developments in economics were later applied to biology largely by John Maynard Smith
in his book Evolution and the Theory of Games
.
In addition to being used to describe, predict, and explain behavior, game theory has also been used to develop theories of ethical or normative behavior and to prescribe such behavior. In economics and philosophy, scholars have applied game theory to help in the understanding of good or proper behavior. Game-theoretic arguments of this type can be found as far back as Plato
.
 The first known use is to describe and model how human populations behave. Some scholars believe that by finding the equilibria of games they can predict how actual human populations will behave when confronted with situations analogous to the game being studied. This particular view of game theory has come under recent criticism. First, it is criticized because the assumptions made by game theorists are often violated. Game theorists may assume players always act in a way to directly maximize their wins (the Homo economicus
The first known use is to describe and model how human populations behave. Some scholars believe that by finding the equilibria of games they can predict how actual human populations will behave when confronted with situations analogous to the game being studied. This particular view of game theory has come under recent criticism. First, it is criticized because the assumptions made by game theorists are often violated. Game theorists may assume players always act in a way to directly maximize their wins (the Homo economicus
model), but in practice, human behavior often deviates from this model. Explanations of this phenomenon are many; irrationality
, new models of deliberation
, or even different motives (like that of altruism
). Game theorists respond by comparing their assumptions to those used in physics. Thus while their assumptions do not always hold, they can treat game theory as a reasonable scientific ideal
akin to the models used by physicist
s. However, additional criticism of this use of game theory has been levied because some experiments have demonstrated that individuals do not play equilibrium strategies. For instance, in the centipede game
, guess 2/3 of the average
game, and the dictator game
, people regularly do not play Nash equilibria. There is an ongoing debate regarding the importance of these experiments.
Alternatively, some authors claim that Nash equilibria do not provide predictions for human populations, but rather provide an explanation for why populations that play Nash equilibria remain in that state. However, the question of how populations reach those points remains open.
Some game theorists have turned to evolutionary game theory
in order to resolve these worries. These models presume either no rationality or bounded rationality
on the part of players. Despite the name, evolutionary game theory does not necessarily presume natural selection
in the biological sense. Evolutionary game theory includes both biological as well as cultural evolution and also models of individual learning (for example, fictitious play
dynamics).
of a game constitutes one's best response
to the actions of the other players, playing a strategy that is part of a Nash equilibrium seems appropriate. However, this use for game theory has also come under criticism. First, in some cases it is appropriate to play a non-equilibrium strategy if one expects others to play non-equilibrium strategies as well. For an example, see Guess 2/3 of the average
.
Second, the Prisoner's dilemma
presents another potential counterexample. In the Prisoner's Dilemma, each player pursuing his own self-interest leads both players to be worse off than had they not pursued their own self-interests.
and business for modeling competing behaviors of interacting agent
s. Applications include a wide array of economic phenomena and approaches, such as auction
s, bargaining
, fair division
, duopolies
, oligopolies
, social network
formation, agent-based computational economics
, general equilibrium
, mechanism design
, and voting system
s, and across such broad areas as behavioral economics, information economics, industrial organization
, and political economy
.
This research usually focuses on particular sets of strategies known as equilibria
in games. These "solution concepts" are usually based on what is required by norms of rationality
. In non-cooperative games, the most famous of these is the Nash equilibrium
. A set of strategies is a Nash equilibrium if each represents a best response to the other strategies. So, if all the players are playing the strategies in a Nash equilibrium, they have no unilateral incentive to deviate, since their strategy is the best they can do given what others are doing.
The payoffs of the game are generally taken to represent the utility
of individual players. Often in modeling situations the payoffs represent money, which presumably corresponds to an individual's utility. This assumption, however, can be faulty.
A prototypical paper on game theory in economics begins by presenting a game that is an abstraction of some particular economic situation. One or more solution concepts are chosen, and the author demonstrates which strategy sets in the presented game are equilibria of the appropriate type. Naturally one might wonder to what use should this information be put. Economists and business professors suggest two primary uses (noted above): descriptive and prescriptive.
is focused in the overlapping areas of fair division
, political economy
, public choice, war bargaining
, positive political theory
, and social choice theory
. In each of these areas, researchers have developed game-theoretic models in which the players are often voters, states, special interest groups, and politicians.
For early examples of game theory applied to political science, see the work of Anthony Downs
. In his book An Economic Theory of Democracy
, he applies the Hotelling firm location model
to the political process. In the Downsian model, political candidates commit to ideologies on a one-dimensional policy space. The theorist shows how the political candidates will converge to the ideology preferred by the median voter.
A game-theoretic explanation for democratic peace
is that public and open debate in democracies send clear and reliable information regarding their intentions to other states. In contrast, it is difficult to know the intentions of nondemocratic leaders, what effect concessions will have, and if promises will be kept. Thus there will be mistrust and unwillingness to make concessions if at least one of the parties in a dispute is a non-democracy .
are often interpreted as corresponding to fitness
. In addition, the focus has been less on equilibria
that correspond to a notion of rationality, but rather on ones that would be maintained by evolution
ary forces. The best known equilibrium in biology is known as the evolutionarily stable strategy
(or ESS), and was first introduced in . Although its initial motivation did not involve any of the mental requirements of the Nash equilibrium
, every ESS is a Nash equilibrium.
In biology, game theory has been used to understand many different phenomena. It was first used to explain the evolution (and stability) of the approximate 1:1 sex ratio
s. suggested that the 1:1 sex ratios are a result of evolutionary forces acting on individuals who could be seen as trying to maximize their number of grandchildren.
Additionally, biologists have used evolutionary game theory
and the ESS to explain the emergence of animal communication
. The analysis of signaling games and other communication games
has provided some insight into the evolution of communication among animals. For example, the mobbing behavior
of many species, in which a large number of prey animals attack a larger predator, seems to be an example of spontaneous emergent organization. Ants have also been shown to exhibit feed-forward behavior akin to fashion, see Butterfly Economics
.
Biologists have used the game of chicken
to analyze fighting behavior and territoriality.
Maynard Smith, in the preface to Evolution and the Theory of Games, writes, "paradoxically, it has turned out that game theory is more readily applied to biology than to the field of economic behaviour for which it was originally designed". Evolutionary game theory has been used to explain many seemingly incongruous phenomena in nature.
One such phenomenon is known as biological altruism
. This is a situation in which an organism appears to act in a way that benefits other organisms and is detrimental to itself. This is distinct from traditional notions of altruism because such actions are not conscious, but appear to be evolutionary adaptations to increase overall fitness. Examples can be found in species ranging from vampire bats that regurgitate blood they have obtained from a night's hunting and give it to group members who have failed to feed, to worker bees that care for the queen bee for their entire lives and never mate, to Vervet monkeys that warn group members of a predator's approach, even when it endangers that individual's chance of survival. All of these actions increase the overall fitness of a group, but occur at a cost to the individual.
Evolutionary game theory explains this altruism with the idea of kin selection
. Altruists discriminate between the individuals they help and favor relatives. Hamilton's rule explains the evolutionary reasoning behind this selection with the equation c
and in computer science
. Several logical theories have a basis in game semantics
. In addition, computer scientists have used games to model interactive computation
s. Also, game theory provides a theoretical basis to the field of multi-agent system
s.
Separately, game theory has played a role in online algorithm
s. In particular, the k-server problem
, which has in the past been referred to as games with moving costs and request-answer games . Yao's principle
is a game-theoretic technique for proving lower bounds on the computational complexity
of randomized algorithm
s, and especially of online algorithms.
The emergence of the internet has motivated the development of algorithms for finding equilibria in games, markets, computational auctions, peer-to-peer systems, and security and information markets. Algorithmic game theory
and within it algorithmic mechanism design
combine computational algorithm design
and analysis of complex system
s with economic theory.
. Responding to two papers by , used game theory to develop a philosophical account of convention
. In so doing, he provided the first analysis of common knowledge
and employed it in analyzing play in coordination game
s. In addition, he first suggested that one can understand meaning
in terms of signaling games. This later suggestion has been pursued by several philosophers since Lewis . Following game-theoretic account of conventions, Ullmann Margalit (1977) and Bicchieri
(2006) have developed theories of social norms that define them as Nash equilibria that result from transforming a mixed-motive game into a coordination game.
Game theory has also challenged philosophers to think in terms of interactive epistemology: what it means for a collective to have common beliefs or knowledge, and what are the consequences of this knowledge for the social outcomes resulting from agents' interactions. Philosophers who have worked in this area include Bicchieri (1989, 1993), Skyrms
(1990), and Stalnaker
(1999).
In ethics
, some authors have attempted to pursue the project, begun by Thomas Hobbes
, of deriving morality from self-interest. Since games like the Prisoner's dilemma
present an apparent conflict between morality and self-interest, explaining why cooperation is required by self-interest is an important component of this project. This general strategy is a component of the general social contract
view in political philosophy
(for examples, see and .
Other authors have attempted to use evolutionary game theory
in order to explain the emergence of human attitudes about morality and corresponding animal behaviors. These authors look at several games including the Prisoner's dilemma, Stag hunt
, and the Nash bargaining game as providing an explanation for the emergence of attitudes about morality (see, e.g., and ).
Some assumptions used in some parts of game theory have been challenged in philosophy; psychological egoism
states that rationality reduces to self-interest—a claim debated among philosophers. (see Psychological egoism#Criticisms)
Often it is assumed that communication among players is allowed in cooperative games, but not in noncooperative ones. This classification on two binary criteria has been rejected .
Of the two types of games, noncooperative games are able to model situations to the finest details, producing accurate results. Cooperative games focus on the game at large. Considerable efforts have been made to link the two approaches. The so-called Nash-programme has already established many of the cooperative solutions as noncooperative equilibria.
Hybrid games contain cooperative and non-cooperative elements. For instance, coalitions of players are formed in a cooperative game
, but these play in a non-cooperative fashion.
, and the stag hunt
are all symmetric games. Some scholars would consider certain asymmetric games as examples of these games as well. However, the most common payoffs for each of these games are symmetric.
Most commonly studied asymmetric games are games where there are not identical strategy sets for both players. For instance, the ultimatum game
and similarly the dictator game
have different strategies for each player. It is possible, however, for a game to have identical strategies for both players, yet be asymmetric. For example, the game pictured to the right is asymmetric despite having identical strategy sets for both players.
games the total benefit to all players in the game, for every combination of strategies, always adds to zero (more informally, a player benefits only at the equal expense of others). Poker
exemplifies a zero-sum game (ignoring the possibility of the house's cut), because one wins exactly the amount one's opponents lose. Other zero-sum games include matching pennies
and most classical board games including Go
and chess
.
Many games studied by game theorists (including the famous prisoner's dilemma
) are non-zero-sum games, because some outcomes
have net results greater or less than zero. Informally, in non-zero-sum games, a gain by one player does not necessarily correspond with a loss by another.
Constant-sum games correspond to activities like theft and gambling, but not to the fundamental economic situation in which there are potential gains from trade
. It is possible to transform any game into a (possibly asymmetric) zero-sum game by adding an additional dummy player (often called "the board"), whose losses compensate the players' net winnings.
s are games where both players move simultaneously, or if they do not move simultaneously, the later players are unaware of the earlier players' actions (making them effectively simultaneous). Sequential game
s (or dynamic games) are games where later players have some knowledge about earlier actions. This need not be perfect information
about every action of earlier players; it might be very little knowledge. For instance, a player may know that an earlier player did not perform one particular action, while he does not know which of the other available actions the first player actually performed.
The difference between simultaneous and sequential games is captured in the different representations discussed above. Often, normal form
is used to represent simultaneous games, and extensive form
is used to represent sequential ones. The transformation of extensive to normal form is one way, meaning that multiple extensive form games correspond to the same normal form. Consequently, notions of equilibrium for simultaneous games are insufficient for reasoning about sequential games; see subgame perfection.
 An important subset of sequential games consists of games of perfect information
An important subset of sequential games consists of games of perfect information
. A game is one of perfect information if all players know the moves previously made by all other players. Thus, only sequential games can be games of perfect information, since in simultaneous games not every player knows the actions of the others. Most games studied in game theory are imperfect-information games, although there are some interesting examples of perfect-information games, including the ultimatum game
and centipede game
. Recreational games of perfect information games include chess
, go
, and mancala
. Many card games are games of imperfect information, for instance poker
or contract bridge
.
Perfect information is often confused with complete information
, which is a similar concept. Complete information requires that every player know the strategies and payoffs available to the other players but not necessarily the actions taken. Games of incomplete information can be reduced, however, to games of imperfect information by introducing "moves by nature
" .
. There is no unified theory addressing combinatorial elements in games. There are, however, mathematical tools that can solve particular problems and answer some general questions.
Games of perfect information have been studied in combinatorial game theory
, which has developed novel representations, e.g. surreal numbers, as well as combinatorial
and algebraic
(and sometimes non-constructive) proof methods to solve games
of certain types, including some "loopy" games that may result in infinitely long sequences of moves. These methods address games with higher combinatorial complexity than those usually considered in traditional (or "economic") game theory. A typical game that has been solved this way is hex
. A related field of study, drawing from computational complexity theory
, is game complexity
, which is concerned with estimating the computational difficulty of finding optimal strategies.
Research in artificial intelligence
has addressed both perfect and imperfect (or incomplete) information games that have very complex combinatorial structures (like chess, go, or backgammon) for which no provable optimal strategies have been found. The practical solutions involve computational heuristics, like alpha-beta pruning
or use of artificial neural network
s trained by reinforcement learning
, which make games more tractable in computing practice.
in particular study games that last for infinitely many moves, with the winner (or other payoff) not known until after all those moves are completed.
The focus of attention is usually not so much on what is the best way to play such a game, but simply on whether one or the other player has a winning strategy. (It can be proven, using the axiom of choice, that there are games—even with perfect information, and where the only outcomes are "win" or "lose"—for which neither player has a winning strategy.) The existence of such strategies, for cleverly designed games, has important consequences in descriptive set theory
.
s allow players to choose a strategy from a continuous strategy set. For instance, Cournot competition
is typically modeled with players' strategies being any non-negative quantities, including fractional quantities.
Differential game
s such as the continuous pursuit and evasion game
are continuous games.
considers games involving a population
of decision makers, where the frequency with which a particular decision is made can change over time in response to the decisions made by all individuals in the population. In biology, this is intended to model (biological) evolution
, where genetically programmed organisms pass along some of their strategy programming to their offspring. In economics, the same theory is intended to capture population changes because people play the game many times within their lifetime, and consciously (and perhaps rationally) switch strategies .
, operations research
, and areas of artificial intelligence
, particularly AI planning (with uncertainty) and multi-agent system
. Although these fields may have different motivators, the mathematics involved are substantially the same, e.g. using Markov decision process
es (MDP).
Stochastic outcomes can also be modeled in terms of game theory by adding a randomly acting player who makes "chance moves", also known as "moves by nature
" . This player is not typically considered a third player in what is otherwise a two-player game, but merely serves to provide a roll of the dice where required by the game.
For some problems, different approaches to modeling stochastic outcomes may lead to different solutions. For example, the difference in approach between MDPs and the minimax solution
is that the latter considers the worst-case over a set of adversarial moves, rather than reasoning in expectation about these moves given a fixed probability distribution. The minimax approach may be advantageous where stochastic models of uncertainty are not available, but may also be overestimating extremely unlikely (but costly) events, dramatically swaying the strategy in such scenarios if it is assumed that an adversary can force such an event to happen. (See black swan theory
for more discussion on this kind of modeling issue, particularly as it relates to predicting and limiting losses in investment banking.)
General models that include all elements of stochastic outcomes, adversaries, and partial or noisy observability (of moves by other players) have also been studied. The "gold standard
" is considered to be partially observable stochastic game
(POSG), but few realistic problems are computationally feasible in POSG representation.
theory.
The term metagame analysis
is also used to refer to a practical approach developed by Nigel Howard whereby a situation is framed as a strategic game in which stakeholders try to realise their objectives by means of the options available to them. Subsequent developments have led to the formulation of drama theory.
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s of conflict and cooperation between intelligent rational
Rational choice theory
Rational choice theory, also known as choice theory or rational action theory, is a framework for understanding and often formally modeling social and economic behavior. It is the main theoretical paradigm in the currently-dominant school of microeconomics...
decision-makers." An alternative term suggested "as a more descriptive name for the discipline" is interactive decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
. Game theory is mainly used in economics, political science, and psychology, and other, more prescribed sciences, like logic or biology. The subject first addressed zero-sum games, such that one person's gains exactly equal net losses of the other participant(s). Today, however, game theory applies to a wide range of class relations, and has developed into an umbrella term
Umbrella term
An umbrella term is a word that provides a superset or grouping of concepts that all fall under a single common category. Umbrella term is also called a hypernym. For example, cryptology is an umbrella term that encompasses cryptography and cryptanalysis, among other fields...
for the logical side of science, to include both human and non-humans, like computers. Classic uses include a sense of balance in numerous games, where each person has found or developed a tactic that cannot successfully better his results, given the other approach.
Mathematical game theory had beginnings with some publications by Émile Borel, which led to his book Applications aux Jeux de Hasard. However, his results were limited, and the theory regarding the non-existence of blended-strategy equilibrium in two-player games was incorrect. Modern game theory began with the idea regarding the existence of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
. Von Neumann's original proof used Brouwer's fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was followed by his 1944 book Theory of Games and Economic Behavior
Theory of Games and Economic Behavior
Theory of Games and Economic Behavior, published in 1944 by Princeton University Press, is a book by mathematician John von Neumann and economist Oskar Morgenstern which is considered the groundbreaking text that created the interdisciplinary research field of game theory...
, with Oskar Morgenstern
Oskar Morgenstern
Oskar Morgenstern was a German-born Austrian-School economist. He, along with John von Neumann, helped found the mathematical field of game theory ....
, which considered cooperative games of several players. The second edition of this book provided an axiomatic theory of expected utility, which allowed mathematical statisticians and economists to treat decision-making under uncertainty.
This theory was developed extensively in the 1950s by many scholars. Game theory was later explicitly applied to biology in the 1970s, although similar developments go back at least as far as the 1930s. Game theory has been widely recognized as an important tool in many fields. Eight game-theorists have won the Nobel Memorial Prize in Economic Sciences
Nobel Memorial Prize in Economic Sciences
The Nobel Memorial Prize in Economic Sciences, commonly referred to as the Nobel Prize in Economics, but officially the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel , is an award for outstanding contributions to the field of economics, generally regarded as one of the...
, and John Maynard Smith
John Maynard Smith
John Maynard Smith,His surname was Maynard Smith, not Smith, nor was it hyphenated. F.R.S. was a British theoretical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J.B.S....
was awarded the Crafoord Prize
Crafoord Prize
The Crafoord Prize is an annual science prize established in 1980 by Holger Crafoord, a Swedish industrialist, and his wife Anna-Greta Crafoord...
for his application of game theory to biology.
History

James Waldegrave, 1st Earl Waldegrave
James Waldegrave, 1st Earl Waldegrave KG PC was a British ambassador.Waldegrave was the son of the 1st Baron Waldegrave and Henrietta FitzJames, the illegitimate daughter of James II and Arabella Churchill....
in 1713. In this letter, Waldegrave provides a minimax
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
mixed strategy solution to a two-person version of the card game le Her
Le Her
Le Her is a gambling game, dating as far back as the 18th century.Le Her is played with a standard deck of 52 cards by two people, designated the dealer and the receiver. King is ranked high and ace low....
. James Madison
James Madison
James Madison, Jr. was an American statesman and political theorist. He was the fourth President of the United States and is hailed as the “Father of the Constitution” for being the primary author of the United States Constitution and at first an opponent of, and then a key author of the United...
made what we now recognize as a game-theoretic analysis of the ways states can be expected to behave under different systems of taxation. In his 1838 Recherches sur les principes mathématiques de la théorie des richesses (Researches into the Mathematical Principles of the Theory of Wealth), Antoine Augustin Cournot
Antoine Augustin Cournot
Antoine Augustin Cournot was a French philosopher and mathematician.Antoine Augustin Cournot was born at Gray, Haute-Saone. In 1821 he entered one of the most prestigious Grande École, the École Normale Supérieure, and in 1829 he had earned a doctoral degree in mathematics, with mechanics as his...
considered a duopoly
Duopoly
A true duopoly is a specific type of oligopoly where only two producers exist in one market. In reality, this definition is generally used where only two firms have dominant control over a market...
and presents a solution that is a restricted version of the Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
.
The Danish mathematician Zeuthen proved that a mathematical model has a winning strategy by using Brouwer's fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
. In his 1938 book Applications aux Jeux de Hasard and earlier notes, Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
1938 book proved a minimax theorem for two-person zero-sum matrix games only when the pay-off matrix was symmetric. Borel conjectured that non-existence of a mixed-strategy equilibria in two-person zero-sum games would occur, a conjecture that was proved false.
Game theory did not really exist as a unique field until John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
published a paper in 1928. Von Neumann's original proof used Brouwer's fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
. His paper was followed by his 1944 book Theory of Games and Economic Behavior
Theory of Games and Economic Behavior
Theory of Games and Economic Behavior, published in 1944 by Princeton University Press, is a book by mathematician John von Neumann and economist Oskar Morgenstern which is considered the groundbreaking text that created the interdisciplinary research field of game theory...
, with Oskar Morgenstern
Oskar Morgenstern
Oskar Morgenstern was a German-born Austrian-School economist. He, along with John von Neumann, helped found the mathematical field of game theory ....
, which considered cooperative games of several players. The second edition of this book provided an axiomatic theory of expected utility, which allowed mathematical statisticians and economists to treat decision-making under uncertainty. Von Neumann's work in game theory culminated in the 1944 book Theory of Games and Economic Behavior
Theory of Games and Economic Behavior
Theory of Games and Economic Behavior, published in 1944 by Princeton University Press, is a book by mathematician John von Neumann and economist Oskar Morgenstern which is considered the groundbreaking text that created the interdisciplinary research field of game theory...
by von Neumann and Oskar Morgenstern
Oskar Morgenstern
Oskar Morgenstern was a German-born Austrian-School economist. He, along with John von Neumann, helped found the mathematical field of game theory ....
. This foundational work contains the method for finding mutually consistent solutions for two-person zero-sum games. During this time period, work on game theory was primarily focused on cooperative game
Cooperative game
In game theory, a cooperative game is a game where groups of players may enforce cooperative behaviour, hence the game is a competition between coalitions of players, rather than between individual players...
theory, which analyzes optimal strategies for groups of individuals, presuming that they can enforce agreements between them about proper strategies.
In 1950, the first discussion of the prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
appeared, and an experiment was undertaken on this game at the RAND corporation. Around this same time, John Nash
John Forbes Nash
John Forbes Nash, Jr. is an American mathematician whose works in game theory, differential geometry, and partial differential equations have provided insight into the forces that govern chance and events inside complex systems in daily life...
developed a criterion for mutual consistency of players' strategies, known as Nash equilibrium, applicable to a wider variety of games than the criterion proposed by von Neumann and Morgenstern. This equilibrium is sufficiently general to allow for the analysis of non-cooperative game
Non-cooperative game
In game theory, a non-cooperative game is one in which players make decisions independently. Thus, while they may be able to cooperate, any cooperation must be self-enforcing....
s in addition to cooperative ones.
Game theory experienced a flurry of activity in the 1950s, during which time the concepts of the core
Core (economics)
The core is the set of feasible allocations that cannot be improved upon by a subset of the economy's consumers. A coalition is said to improve upon or block a feasible allocation if the members of that coalition are better off under another feasible allocation that is identical to the first...
, the extensive form game
Extensive form game
An extensive-form game is a specification of a game in game theory, allowing explicit representation of a number of important aspects, like the sequencing of players' possible moves, their choices at every decision point, the information each player has about the other player's moves when he...
, fictitious play
Fictitious play
In game theory, fictitious play is a learning rule first introduced by G.W. Brown . In it, each player presumes that the opponents are playing stationary strategies. At each round, each player thus best responds to the empirical frequency of play of his opponent...
, repeated game
Repeated game
In game theory, a repeated game is an extensive form game which consists in some number of repetitions of some base game . The stage game is usually one of the well-studied 2-person games...
s, and the Shapley value
Shapley value
In game theory, the Shapley value, named in honour of Lloyd Shapley, who introduced it in 1953, is a solution concept in cooperative game theory. To each cooperative game it assigns a unique distribution of a total surplus generated by the coalition of all players...
were developed. In addition, the first applications of Game theory to philosophy
Philosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
and political science
Political science
Political Science is a social science discipline concerned with the study of the state, government and politics. Aristotle defined it as the study of the state. It deals extensively with the theory and practice of politics, and the analysis of political systems and political behavior...
occurred during this time.
In 1965, Reinhard Selten
Reinhard Selten
-Life and career:Selten was born in Breslau in Lower Silesia, now in Poland, to a Jewish father, Adolf Selten, and Protestant mother, Käthe Luther. For his work in game theory, Selten won the 1994 Nobel Memorial Prize in Economic Sciences...
introduced his solution concept
Solution concept
In game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
of subgame perfect equilibria
Subgame perfect equilibrium
In game theory, a subgame perfect equilibrium is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game...
, which further refined the Nash equilibrium (later he would introduce trembling hand perfection as well). In 1967, John Harsanyi
John Harsanyi
John Charles Harsanyi was a Hungarian-Australian-American economist and Nobel Memorial Prize in Economic Sciences winner....
developed the concepts of complete information
Complete information
Complete information is a term used in economics and game theory to describe an economic situation or game in which knowledge about other market participants or players is available to all participants. Every player knows the payoffs and strategies available to other players.Complete information...
and Bayesian game
Bayesian game
In game theory, a Bayesian game is one in which information about characteristics of the other players is incomplete. Following John C. Harsanyi's framework, a Bayesian game can be modelled by introducing Nature as a player in a game...
s. Nash, Selten and Harsanyi became Economics Nobel Laureates
Nobel Memorial Prize in Economic Sciences
The Nobel Memorial Prize in Economic Sciences, commonly referred to as the Nobel Prize in Economics, but officially the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel , is an award for outstanding contributions to the field of economics, generally regarded as one of the...
in 1994 for their contributions to economic game theory.
In the 1970s, game theory was extensively applied in biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, largely as a result of the work of John Maynard Smith
John Maynard Smith
John Maynard Smith,His surname was Maynard Smith, not Smith, nor was it hyphenated. F.R.S. was a British theoretical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J.B.S....
and his evolutionarily stable strategy
Evolutionarily stable strategy
In game theory and behavioural ecology, an evolutionarily stable strategy , which is sometimes also called an evolutionary stable strategy, is a strategy which, if adopted by a population of players, cannot be invaded by any alternative strategy that is initially rare. An ESS is an equilibrium...
. In addition, the concepts of correlated equilibrium
Correlated equilibrium
In game theory, a correlated equilibrium is a solution concept that is more general than the well known Nash equilibrium. It was first discussed by mathematician Robert Aumann . The idea is that each player chooses his/her action according to his/her observation of the value of the same public...
, trembling hand perfection, and common knowledge
Common knowledge (logic)
Common knowledge is a special kind of knowledge for a group of agents. There is common knowledge of p in a group of agents G when all the agents in G know p, they all know that they know p, they all know that they all know that they know p, and so on ad infinitum.The concept was first introduced in...
were introduced and analyzed.
In 2005, game theorists Thomas Schelling
Thomas Schelling
Thomas Crombie Schelling is an American economist and professor of foreign affairs, national security, nuclear strategy, and arms control at the School of Public Policy at University of Maryland, College Park. He is also co-faculty at the New England Complex Systems Institute...
and Robert Aumann followed Nash, Selten and Harsanyi as Nobel Laureates. Schelling worked on dynamic models, early examples of evolutionary game theory
Evolutionary game theory
Evolutionary game theory is the application of Game Theory to evolving populations of lifeforms in biology. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith...
. Aumann contributed more to the equilibrium school, introducing an equilibrium coarsening, correlated equilibrium, and developing an extensive formal analysis of the assumption of common knowledge and of its consequences.
In 2007, Leonid Hurwicz
Leonid Hurwicz
Leonid "Leo" Hurwicz was a Russian-born American economist and mathematician. His nationality of origin was Polish. He was Jewish. He originated incentive compatibility and mechanism design, which show how desired outcomes are achieved in economics, social science and political science...
, together with Eric Maskin
Eric Maskin
Eric Stark Maskin is an American economist and Nobel laureate recognized with Leonid Hurwicz and Roger Myerson "for having laid the foundations of mechanism design theory." He is the Albert O...
and Roger Myerson
Roger Myerson
Roger Bruce Myerson is an American economist and Nobel laureate recognized with Leonid Hurwicz and Eric Maskin for "having laid the foundations of mechanism design theory." A professor at the University of Chicago, he has made contributions as an economist, as an applied mathematician, and as a...
, was awarded the Nobel Prize in Economics "for having laid the foundations of mechanism design
Mechanism design
Mechanism design is a field in game theory studying solution concepts for a class of private information games...
theory." Myerson's contributions include the notion of proper equilibrium
Proper equilibrium
Proper equilibrium is a refinement of Nash Equilibrium due to Roger B. Myerson.Proper equilibrium further refines Reinhard Selten's notion of atrembling hand perfect equilibrium by assuming that more costly trembles are made with...
, and an important graduate text: Game Theory, Analysis of Conflict . Hurwicz introduced and formalized the concept of incentive compatibility
Incentive compatibility
In mechanism design, a process is said to be incentive-compatible if all of the participants fare best when they truthfully reveal any private information asked for by the mechanism. As an illustration, voting systems which create incentives to vote dishonestly lack the property of incentive...
.
Representation of games
The games studied in game theory are well-defined mathematical objects. A game consists of a set of playerPlayer (game)
A player of a game is a participant therein. The term 'player' is used with this same meaning both in game theory and in ordinary recreational games....
s, a set of moves (or strategies
Strategy (game theory)
In game theory, a player's strategy in a game is a complete plan of action for whatever situation might arise; this fully determines the player's behaviour...
) available to those players, and a specification of payoffs for each combination of strategies. Most cooperative games are presented in the characteristic function form, while the extensive and the normal forms are used to define noncooperative games.
Extensive form

Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
(as pictured to the left). Here each vertex
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
(or node) represents a point of choice for a player. The player is specified by a number listed by the vertex. The lines out of the vertex represent a possible action for that player. The payoffs are specified at the bottom of the tree. The extensive form can be viewed as a multi-player generalization of a decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
.
In the game pictured to the left, there are two players. Player 1 moves first and chooses either F or U. Player 2 sees Player 1s move and then chooses A or R. Suppose that Player 1 chooses U and then Player 2 chooses A, then Player 1 gets 8 and Player 2 gets 2.
The extensive form can also capture simultaneous-move games and games with imperfect information. To represent it, either a dotted line connects different vertices to represent them as being part of the same information set (i.e., the players do not know at which point they are), or a closed line is drawn around them. (See example in the imperfect information section.)
Normal form
The normal (or strategic form) game is usually represented by a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which shows the players, strategies, and payoffs (see the example to the right). More generally it can be represented by any function that associates a payoff for each player with every possible combination of actions. In the accompanying example there are two players; one chooses the row and the other chooses the column. Each player has two strategies, which are specified by the number of rows and the number of columns. The payoffs are provided in the interior. The first number is the payoff received by the row player (Player 1 in our example); the second is the payoff for the column player (Player 2 in our example). Suppose that Player 1 plays Up and that Player 2 plays Left. Then Player 1 gets a payoff of 4, and Player 2 gets 3.
When a game is presented in normal form, it is presumed that each player acts simultaneously or, at least, without knowing the actions of the other. If players have some information about the choices of other players, the game is usually presented in extensive form.
Every extensive-form game has an equivalent normal-form game, however the transformation to normal form may result in an exponential blowup in the size of the representation, making it computationally impractical.
Characteristic function form
In games that possess removable utility separate rewards are not given; rather, the characteristic function decides the payoff of each unity. The idea is that the unity that is 'empty', so to speak, does not receive a reward at all.The origin of this form is to be found in John von Neumann and Oskar Morgenstern's book; when looking at these instances, they guessed that when a union C appears, it works against the fraction (N/C) as if two individuals were playing a normal game. The balanced payoff of C is a basic function. Although there are differing examples that help determine coalitional amounts from normal games, not all appear that in their function form can be derived from such.
Formally, a characteristic function is seen as: (N,v), where N represents the group of people and v:2^N-->R is a normal utility.
Such characteristic functions have expanded to describe games where there is no removable utility.
Partition function form
The characteristic function form ignores the possible externalitiesExternality
In economics, an externality is a cost or benefit, not transmitted through prices, incurred by a party who did not agree to the action causing the cost or benefit...
of coalition formation. In the partition function form the payoff of a coalition depends not only on its members, but also on the way the rest of the players are partitioned .
General and applied uses
As a method of applied mathematicsApplied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, game theory has been used to study a wide variety of human and animal behaviors. It was initially developed in economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
to understand a large collection of economic behaviors, including behaviors of firms, markets, and consumers. The use of game theory in the social sciences has expanded, and game theory has been applied to political, sociological, and psychological behaviors as well.
Game-theoretic analysis was initially used to study animal behavior by Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
in the 1930s (although even Charles Darwin
Charles Darwin
Charles Robert Darwin FRS was an English naturalist. He established that all species of life have descended over time from common ancestry, and proposed the scientific theory that this branching pattern of evolution resulted from a process that he called natural selection.He published his theory...
makes a few informal game-theoretic statements). This work predates the name "game theory", but it shares many important features with this field. The developments in economics were later applied to biology largely by John Maynard Smith
John Maynard Smith
John Maynard Smith,His surname was Maynard Smith, not Smith, nor was it hyphenated. F.R.S. was a British theoretical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J.B.S....
in his book Evolution and the Theory of Games
Evolution and the Theory of Games
Evolution and the Theory of Games is a 1982 book by the British evolutionary biologist John Maynard Smith on evolutionary game theory. In it, Maynard Smith summarises work on evolutionary game theory that had developed in the 1970s, to which he made several important contributions...
.
In addition to being used to describe, predict, and explain behavior, game theory has also been used to develop theories of ethical or normative behavior and to prescribe such behavior. In economics and philosophy, scholars have applied game theory to help in the understanding of good or proper behavior. Game-theoretic arguments of this type can be found as far back as Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
.
Description and modeling

Homo economicus
Homo economicus, or Economic human, is the concept in some economic theories of humans as rational and narrowly self-interested actors who have the ability to make judgments toward their subjectively defined ends...
model), but in practice, human behavior often deviates from this model. Explanations of this phenomenon are many; irrationality
Irrationality
Irrationality is cognition, thinking, talking or acting without inclusion of rationality. It is more specifically described as an action or opinion given through inadequate reasoning, emotional distress, or cognitive deficiency...
, new models of deliberation
Deliberation
Deliberation is a process of thoughtfully weighing options, usually prior to voting. In legal settings a jury famously uses deliberation because it is given specific options, like guilty or not guilty, along with information and arguments to evaluate. Deliberation emphasizes the use of logic and...
, or even different motives (like that of altruism
Altruism
Altruism is a concern for the welfare of others. It is a traditional virtue in many cultures, and a core aspect of various religious traditions, though the concept of 'others' toward whom concern should be directed can vary among cultures and religions. Altruism is the opposite of...
). Game theorists respond by comparing their assumptions to those used in physics. Thus while their assumptions do not always hold, they can treat game theory as a reasonable scientific ideal
Idealization
Idealization is the process by which scientific models assume facts about the phenomenon being modeled that are strictly false. Often these assumptions are used to make models easier to understand or solve. Many times idealizations do not harm the predictive accuracy of the model for one reason or...
akin to the models used by physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
s. However, additional criticism of this use of game theory has been levied because some experiments have demonstrated that individuals do not play equilibrium strategies. For instance, in the centipede game
Centipede game
In game theory, the centipede game, first introduced by Rosenthal , is an extensive form game in which two players take turns choosing either to take a slightly larger share of a slowly increasing pot, or to pass the pot to the other player...
, guess 2/3 of the average
Guess 2/3 of the average
In game theory, Guess 2/3 of the average is a game where several people guess what 2/3 of the average of their guesses will be, and where the numbers are restricted to the real numbers between 0 and 100, inclusive. The winner is the one closest to the 2/3 average.- Equilibrium analysis :In this...
game, and the dictator game
Dictator game
The dictator game is a game in experimental economics, similar to the ultimatum game. Experimental results offer evidence against the rationally self-interested individual concept of economic behavior, though precisely what to conclude from the evidence is controversial.-Description:In the...
, people regularly do not play Nash equilibria. There is an ongoing debate regarding the importance of these experiments.
Alternatively, some authors claim that Nash equilibria do not provide predictions for human populations, but rather provide an explanation for why populations that play Nash equilibria remain in that state. However, the question of how populations reach those points remains open.
Some game theorists have turned to evolutionary game theory
Evolutionary game theory
Evolutionary game theory is the application of Game Theory to evolving populations of lifeforms in biology. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith...
in order to resolve these worries. These models presume either no rationality or bounded rationality
Bounded rationality
Bounded rationality is the idea that in decision making, rationality of individuals is limited by the information they have, the cognitive limitations of their minds, and the finite amount of time they have to make a decision...
on the part of players. Despite the name, evolutionary game theory does not necessarily presume natural selection
Natural selection
Natural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....
in the biological sense. Evolutionary game theory includes both biological as well as cultural evolution and also models of individual learning (for example, fictitious play
Fictitious play
In game theory, fictitious play is a learning rule first introduced by G.W. Brown . In it, each player presumes that the opponents are playing stationary strategies. At each round, each player thus best responds to the empirical frequency of play of his opponent...
dynamics).
Prescriptive or normative analysis
On the other hand, some scholars see game theory not as a predictive tool for the behavior of human beings, but as a suggestion for how people ought to behave. Since a Nash equilibriumNash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
of a game constitutes one's best response
Best response
In game theory, the best response is the strategy which produces the most favorable outcome for a player, taking other players' strategies as given...
to the actions of the other players, playing a strategy that is part of a Nash equilibrium seems appropriate. However, this use for game theory has also come under criticism. First, in some cases it is appropriate to play a non-equilibrium strategy if one expects others to play non-equilibrium strategies as well. For an example, see Guess 2/3 of the average
Guess 2/3 of the average
In game theory, Guess 2/3 of the average is a game where several people guess what 2/3 of the average of their guesses will be, and where the numbers are restricted to the real numbers between 0 and 100, inclusive. The winner is the one closest to the 2/3 average.- Equilibrium analysis :In this...
.
Second, the Prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
presents another potential counterexample. In the Prisoner's Dilemma, each player pursuing his own self-interest leads both players to be worse off than had they not pursued their own self-interests.
Economics and business
Game theory is a major method used in mathematical economicsMathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
and business for modeling competing behaviors of interacting agent
Agent (economics)
In economics, an agent is an actor and decision maker in a model. Typically, every agent makes decisions by solving a well or ill defined optimization/choice problem. The term agent can also be seen as equivalent to player in game theory....
s. Applications include a wide array of economic phenomena and approaches, such as auction
Auction
An auction is a process of buying and selling goods or services by offering them up for bid, taking bids, and then selling the item to the highest bidder...
s, bargaining
Bargaining
Bargaining or haggling is a type of negotiation in which the buyer and seller of a good or service dispute the price which will be paid and the exact nature of the transaction that will take place, and eventually come to an agreement. Bargaining is an alternative pricing strategy to fixed prices...
, fair division
Fair division
Fair division, also known as the cake-cutting problem, is the problem of dividing a resource in such a way that all recipients believe that they have received a fair amount...
, duopolies
Duopoly
A true duopoly is a specific type of oligopoly where only two producers exist in one market. In reality, this definition is generally used where only two firms have dominant control over a market...
, oligopolies
Oligopoly
An oligopoly is a market form in which a market or industry is dominated by a small number of sellers . The word is derived, by analogy with "monopoly", from the Greek ὀλίγοι "few" + πόλειν "to sell". Because there are few sellers, each oligopolist is likely to be aware of the actions of the others...
, social network
Social network
A social network is a social structure made up of individuals called "nodes", which are tied by one or more specific types of interdependency, such as friendship, kinship, common interest, financial exchange, dislike, sexual relationships, or relationships of beliefs, knowledge or prestige.Social...
formation, agent-based computational economics
Agent-Based Computational Economics
Agent-based computational economics is the major aspect of computational economics that studies economic processes, including whole economies, as dynamic systems of interacting agents. As such, it falls in paradigm of complex adaptive systems...
, general equilibrium
General equilibrium
General equilibrium theory is a branch of theoretical economics. It seeks to explain the behavior of supply, demand and prices in a whole economy with several or many interacting markets, by seeking to prove that a set of prices exists that will result in an overall equilibrium, hence general...
, mechanism design
Mechanism design
Mechanism design is a field in game theory studying solution concepts for a class of private information games...
, and voting system
Voting system
A voting system or electoral system is a method by which voters make a choice between options, often in an election or on a policy referendum....
s, and across such broad areas as behavioral economics, information economics, industrial organization
Industrial organization
Industrial organization is the field of economics that builds on the theory of the firm in examining the structure of, and boundaries between, firms and markets....
, and political economy
Political economy
Political economy originally was the term for studying production, buying, and selling, and their relations with law, custom, and government, as well as with the distribution of national income and wealth, including through the budget process. Political economy originated in moral philosophy...
.
This research usually focuses on particular sets of strategies known as equilibria
Solution concept
In game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
in games. These "solution concepts" are usually based on what is required by norms of rationality
Perfect rationality
In economics and game theory, the participants are sometimes considered to have perfect rationality: that is, they always act in a way that maximizes their utility, and are capable of arbitrarily complex deductions towards that end...
. In non-cooperative games, the most famous of these is the Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. A set of strategies is a Nash equilibrium if each represents a best response to the other strategies. So, if all the players are playing the strategies in a Nash equilibrium, they have no unilateral incentive to deviate, since their strategy is the best they can do given what others are doing.
The payoffs of the game are generally taken to represent the utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
of individual players. Often in modeling situations the payoffs represent money, which presumably corresponds to an individual's utility. This assumption, however, can be faulty.
A prototypical paper on game theory in economics begins by presenting a game that is an abstraction of some particular economic situation. One or more solution concepts are chosen, and the author demonstrates which strategy sets in the presented game are equilibria of the appropriate type. Naturally one might wonder to what use should this information be put. Economists and business professors suggest two primary uses (noted above): descriptive and prescriptive.
Political science
The application of game theory to political sciencePolitical science
Political Science is a social science discipline concerned with the study of the state, government and politics. Aristotle defined it as the study of the state. It deals extensively with the theory and practice of politics, and the analysis of political systems and political behavior...
is focused in the overlapping areas of fair division
Fair division
Fair division, also known as the cake-cutting problem, is the problem of dividing a resource in such a way that all recipients believe that they have received a fair amount...
, political economy
Political economy
Political economy originally was the term for studying production, buying, and selling, and their relations with law, custom, and government, as well as with the distribution of national income and wealth, including through the budget process. Political economy originated in moral philosophy...
, public choice, war bargaining
War's inefficiency puzzle
War’s inefficiency puzzle is a research question asking why unitary-actor states would choose to fight wars when doing so is costly. James Fearon’s Rationalist Explanations for War and Robert Powell's In the Shadow of Power, which launched rational choice theory in international relations, provide...
, positive political theory
Positive political theory
Positive political theory or explanatory political theory is the study of politics using formal methods such as social choice theory, game theory, and statistical analysis. In particular, social choice theoretic methods are often used to describe and analyze the performance of rules or institutions...
, and social choice theory
Social choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
. In each of these areas, researchers have developed game-theoretic models in which the players are often voters, states, special interest groups, and politicians.
For early examples of game theory applied to political science, see the work of Anthony Downs
Anthony Downs
Anthony Downs is a scholar in public policy and public administration, and since 1977 is a Senior Fellow at the Brookings Institution in Washington D.C..-Education:...
. In his book An Economic Theory of Democracy
An Economic Theory of Democracy
An Economic Theory of Democracy is a political science treatise written by Anthony Downs, published in 1957. The book set forth a model with precise conditions under which economic theory could be applied to non-market political decision-making. It also suggested areas of empirical research that...
, he applies the Hotelling firm location model
Hotelling's law
Hotelling's law is an observation in economics that in many markets it is rational for producers to make their products as similar as possible. This is also referred to as the principle of minimum differentiation as well as Hotelling's "linear city model"...
to the political process. In the Downsian model, political candidates commit to ideologies on a one-dimensional policy space. The theorist shows how the political candidates will converge to the ideology preferred by the median voter.
A game-theoretic explanation for democratic peace
Democratic peace theory
Democratic peace theory is the theory that democracies don't go to war with each other. How well the theory matches reality depends a great deal on one's definition of "democracy" and "war"...
is that public and open debate in democracies send clear and reliable information regarding their intentions to other states. In contrast, it is difficult to know the intentions of nondemocratic leaders, what effect concessions will have, and if promises will be kept. Thus there will be mistrust and unwillingness to make concessions if at least one of the parties in a dispute is a non-democracy .
Biology
Unlike economics, the payoffs for games in biologyBiology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
are often interpreted as corresponding to fitness
Fitness (biology)
Fitness is a central idea in evolutionary theory. It can be defined either with respect to a genotype or to a phenotype in a given environment...
. In addition, the focus has been less on equilibria
Solution concept
In game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
that correspond to a notion of rationality, but rather on ones that would be maintained by evolution
Evolution
Evolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
ary forces. The best known equilibrium in biology is known as the evolutionarily stable strategy
Evolutionarily stable strategy
In game theory and behavioural ecology, an evolutionarily stable strategy , which is sometimes also called an evolutionary stable strategy, is a strategy which, if adopted by a population of players, cannot be invaded by any alternative strategy that is initially rare. An ESS is an equilibrium...
(or ESS), and was first introduced in . Although its initial motivation did not involve any of the mental requirements of the Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
, every ESS is a Nash equilibrium.
In biology, game theory has been used to understand many different phenomena. It was first used to explain the evolution (and stability) of the approximate 1:1 sex ratio
Sex ratio
Sex ratio is the ratio of males to females in a population. The primary sex ratio is the ratio at the time of conception, secondary sex ratio is the ratio at time of birth, and tertiary sex ratio is the ratio of mature organisms....
s. suggested that the 1:1 sex ratios are a result of evolutionary forces acting on individuals who could be seen as trying to maximize their number of grandchildren.
Additionally, biologists have used evolutionary game theory
Evolutionary game theory
Evolutionary game theory is the application of Game Theory to evolving populations of lifeforms in biology. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith...
and the ESS to explain the emergence of animal communication
Animal communication
Animal communication is any behavior on the part of one animal that has an effect on the current or future behaviour of another animal. The study of animal communication, is sometimes called Zoosemiotics has played an important part in the...
. The analysis of signaling games and other communication games
Cheap talk
In game theory, cheap talk is communication between players which does not directly affect the payoffs of the game. This is in contrast to signaling in which sending certain messages may be costly for the sender depending on the state of the world...
has provided some insight into the evolution of communication among animals. For example, the mobbing behavior
Mobbing behavior
Mobbing in animals is an antipredator behavior which occurs when individuals of a certain species mob a predator by cooperatively attacking or harassing it, usually to protect their offspring. A simple definition of mobbing is an assemblage of individuals around a potentially dangerous predator...
of many species, in which a large number of prey animals attack a larger predator, seems to be an example of spontaneous emergent organization. Ants have also been shown to exhibit feed-forward behavior akin to fashion, see Butterfly Economics
Butterfly Economics
Butterfly Economics: A New General Theory of Social and Economic Behavior is a book by Paul Ormerod dealing with economic theory, published in 1999...
.
Biologists have used the game of chicken
Chicken (game)
The game of chicken, also known as the hawk-dove or snowdrift game, is an influential model of conflict for two players in game theory...
to analyze fighting behavior and territoriality.
Maynard Smith, in the preface to Evolution and the Theory of Games, writes, "paradoxically, it has turned out that game theory is more readily applied to biology than to the field of economic behaviour for which it was originally designed". Evolutionary game theory has been used to explain many seemingly incongruous phenomena in nature.
One such phenomenon is known as biological altruism
Altruism in animals
Altruism is a well-documented animal behaviour, which appears most obviously in kin relationships but may also be evident amongst wider social groups, in which an animal sacrifices its own well-being for the benefit of another animal.- Overview :...
. This is a situation in which an organism appears to act in a way that benefits other organisms and is detrimental to itself. This is distinct from traditional notions of altruism because such actions are not conscious, but appear to be evolutionary adaptations to increase overall fitness. Examples can be found in species ranging from vampire bats that regurgitate blood they have obtained from a night's hunting and give it to group members who have failed to feed, to worker bees that care for the queen bee for their entire lives and never mate, to Vervet monkeys that warn group members of a predator's approach, even when it endangers that individual's chance of survival. All of these actions increase the overall fitness of a group, but occur at a cost to the individual.
Evolutionary game theory explains this altruism with the idea of kin selection
Kin selection
Kin selection refers to apparent strategies in evolution that favor the reproductive success of an organism's relatives, even at a cost to the organism's own survival and reproduction. Charles Darwin was the first to discuss the concept of group/kin selection...
. Altruists discriminate between the individuals they help and favor relatives. Hamilton's rule explains the evolutionary reasoning behind this selection with the equation c
Computer science and logic
Game theory has come to play an increasingly important role in logicLogic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. Several logical theories have a basis in game semantics
Game semantics
Game semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. In the late 1950s Paul Lorenzen was the...
. In addition, computer scientists have used games to model interactive computation
Interactive computation
In computer science, interactive computation is a mathematical model for computation that involves communication with the external world during the computation...
s. Also, game theory provides a theoretical basis to the field of multi-agent system
Multi-agent system
A multi-agent system is a system composed of multiple interacting intelligent agents. Multi-agent systems can be used to solve problems that are difficult or impossible for an individual agent or a monolithic system to solve...
s.
Separately, game theory has played a role in online algorithm
Online algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from...
s. In particular, the k-server problem
K-server problem
The k-server problem is a problem of theoretical computer science in the category of online algorithms, one of two abstract problems on metric spaces that are central to the theory of competitive analysis...
, which has in the past been referred to as games with moving costs and request-answer games . Yao's principle
Yao's Principle
In computational complexity theory, Yao's principle or Yao's minimax principle states that the expected cost of any randomized algorithm for solving a given problem, on the worst case input for that algorithm, can be no better than the expected cost, for a worst-case random probability distribution...
is a game-theoretic technique for proving lower bounds on the computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s, and especially of online algorithms.
The emergence of the internet has motivated the development of algorithms for finding equilibria in games, markets, computational auctions, peer-to-peer systems, and security and information markets. Algorithmic game theory
Algorithmic game theory
Algorithmic game theory is an area in the intersection of game theory and algorithm design, whose objective is to design algorithms in strategic environments. Typically, in Algorithmic Game Theory problems, the input to a given algorithm is distributed among many players who have a personal...
and within it algorithmic mechanism design
Algorithmic mechanism design
Algorithmic mechanism design lies at the intersection of economic game theory and computer science.Noam Nisan and Amir Ronen, from the Hebrew University of Jerusalem, first coined "Algorithmic mechanism design" in a research paper published in 2001....
combine computational algorithm design
Algorithm design
Algorithm design is a specific method to create a mathematical process in solving problems. Applied algorithm design is algorithm engineering....
and analysis of complex system
Complex system
A complex system is a system composed of interconnected parts that as a whole exhibit one or more properties not obvious from the properties of the individual parts....
s with economic theory.
Philosophy
Game theory has been put to several uses in philosophyPhilosophy
Philosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
. Responding to two papers by , used game theory to develop a philosophical account of convention
Convention (norm)
A convention is a set of agreed, stipulated or generally accepted standards, norms, social norms or criteria, often taking the form of a custom....
. In so doing, he provided the first analysis of common knowledge
Common knowledge (logic)
Common knowledge is a special kind of knowledge for a group of agents. There is common knowledge of p in a group of agents G when all the agents in G know p, they all know that they know p, they all know that they all know that they know p, and so on ad infinitum.The concept was first introduced in...
and employed it in analyzing play in coordination game
Coordination game
In game theory, coordination games are a class of games with multiple pure strategy Nash equilibria in which players choose the same or corresponding strategies...
s. In addition, he first suggested that one can understand meaning
Meaning (semiotics)
In semiotics, the meaning of a sign is its place in a sign relation, in other words, the set of roles that it occupies within a given sign relation. This statement holds whether sign is taken to mean a sign type or a sign token...
in terms of signaling games. This later suggestion has been pursued by several philosophers since Lewis . Following game-theoretic account of conventions, Ullmann Margalit (1977) and Bicchieri
Cristina Bicchieri
Cristina Bicchieri is the S.J.P. Harvie Professor of Social Thought and Comparative Ethics in the Philosophy Department at the University of Pennsylvania, and director of the Philosophy, Politics and Economics program. She is also a Professor in the Legal Sudies department of the Wharton School,...
(2006) have developed theories of social norms that define them as Nash equilibria that result from transforming a mixed-motive game into a coordination game.
Game theory has also challenged philosophers to think in terms of interactive epistemology: what it means for a collective to have common beliefs or knowledge, and what are the consequences of this knowledge for the social outcomes resulting from agents' interactions. Philosophers who have worked in this area include Bicchieri (1989, 1993), Skyrms
Brian Skyrms
Brian Skyrms is a Distinguished Professor of Logic and Philosophy of Science and Economics at the University of California, Irvine and a Professor of Philosophy at Stanford University. He has worked on problems in the philosophy of science, causation, decision theory, game theory, and the...
(1990), and Stalnaker
Robert Stalnaker
Robert C. Stalnaker is Laurance S. Rockefeller Professor of Philosophy at the Massachusetts Institute of Technology. In 2007, he delivered the John Locke Lectures at Oxford University on the topic of Our Knowledge of the Internal World...
(1999).
In ethics
Ethics
Ethics, also known as moral philosophy, is a branch of philosophy that addresses questions about morality—that is, concepts such as good and evil, right and wrong, virtue and vice, justice and crime, etc.Major branches of ethics include:...
, some authors have attempted to pursue the project, begun by Thomas Hobbes
Thomas Hobbes
Thomas Hobbes of Malmesbury , in some older texts Thomas Hobbs of Malmsbury, was an English philosopher, best known today for his work on political philosophy...
, of deriving morality from self-interest. Since games like the Prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
present an apparent conflict between morality and self-interest, explaining why cooperation is required by self-interest is an important component of this project. This general strategy is a component of the general social contract
Social contract
The social contract is an intellectual device intended to explain the appropriate relationship between individuals and their governments. Social contract arguments assert that individuals unite into political societies by a process of mutual consent, agreeing to abide by common rules and accept...
view in political philosophy
Political philosophy
Political philosophy is the study of such topics as liberty, justice, property, rights, law, and the enforcement of a legal code by authority: what they are, why they are needed, what, if anything, makes a government legitimate, what rights and freedoms it should protect and why, what form it...
(for examples, see and .
Other authors have attempted to use evolutionary game theory
Evolutionary game theory
Evolutionary game theory is the application of Game Theory to evolving populations of lifeforms in biology. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith...
in order to explain the emergence of human attitudes about morality and corresponding animal behaviors. These authors look at several games including the Prisoner's dilemma, Stag hunt
Stag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
, and the Nash bargaining game as providing an explanation for the emergence of attitudes about morality (see, e.g., and ).
Some assumptions used in some parts of game theory have been challenged in philosophy; psychological egoism
Psychological egoism
Psychological egoism is the view that humans are always motivated by self-interest, even in what seem to be acts of altruism. It claims that, when people choose to help others, they do so ultimately because of the personal benefits that they themselves expect to obtain, directly or indirectly,...
states that rationality reduces to self-interest—a claim debated among philosophers. (see Psychological egoism#Criticisms)
Cooperative or non-cooperative
A game is cooperative if the players are able to form binding commitments. For instance the legal system requires them to adhere to their promises. In noncooperative games this is not possible.Often it is assumed that communication among players is allowed in cooperative games, but not in noncooperative ones. This classification on two binary criteria has been rejected .
Of the two types of games, noncooperative games are able to model situations to the finest details, producing accurate results. Cooperative games focus on the game at large. Considerable efforts have been made to link the two approaches. The so-called Nash-programme has already established many of the cooperative solutions as noncooperative equilibria.
Hybrid games contain cooperative and non-cooperative elements. For instance, coalitions of players are formed in a cooperative game
Cooperative game
In game theory, a cooperative game is a game where groups of players may enforce cooperative behaviour, hence the game is a competition between coalitions of players, rather than between individual players...
, but these play in a non-cooperative fashion.
Symmetric and asymmetric
A symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If the identities of the players can be changed without changing the payoff to the strategies, then a game is symmetric. Many of the commonly studied 2×2 games are symmetric. The standard representations of chicken, the prisoner's dilemmaPrisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
, and the stag hunt
Stag hunt
In game theory, the stag hunt is a game which describes a conflict between safety and social cooperation. Other names for it or its variants include "assurance game", "coordination game", and "trust dilemma". Jean-Jacques Rousseau described a situation in which two individuals go out on a hunt. ...
are all symmetric games. Some scholars would consider certain asymmetric games as examples of these games as well. However, the most common payoffs for each of these games are symmetric.
Most commonly studied asymmetric games are games where there are not identical strategy sets for both players. For instance, the ultimatum game
Ultimatum game
The ultimatum game is a game often played in economic experiments in which two players interact to decide how to divide a sum of money that is given to them. The first player proposes how to divide the sum between the two players, and the second player can either accept or reject this proposal. ...
and similarly the dictator game
Dictator game
The dictator game is a game in experimental economics, similar to the ultimatum game. Experimental results offer evidence against the rationally self-interested individual concept of economic behavior, though precisely what to conclude from the evidence is controversial.-Description:In the...
have different strategies for each player. It is possible, however, for a game to have identical strategies for both players, yet be asymmetric. For example, the game pictured to the right is asymmetric despite having identical strategy sets for both players.
Zero-sum and non-zero-sum
Zero-sum games are a special case of constant-sum games, in which choices by players can neither increase nor decrease the available resources. In zero-sumZero-sum
In game theory and economic theory, a zero-sum game is a mathematical representation of a situation in which a participant's gain of utility is exactly balanced by the losses of the utility of other participant. If the total gains of the participants are added up, and the total losses are...
games the total benefit to all players in the game, for every combination of strategies, always adds to zero (more informally, a player benefits only at the equal expense of others). Poker
Poker
Poker is a family of card games that share betting rules and usually hand rankings. Poker games differ in how the cards are dealt, how hands may be formed, whether the high or low hand wins the pot in a showdown , limits on bet sizes, and how many rounds of betting are allowed.In most modern poker...
exemplifies a zero-sum game (ignoring the possibility of the house's cut), because one wins exactly the amount one's opponents lose. Other zero-sum games include matching pennies
Matching pennies
Matching pennies is the name for a simple example game used in game theory. It is the two strategy equivalent of Rock, Paper, Scissors. Matching pennies is used primarily to illustrate the concept of mixed strategies and a mixed strategy Nash equilibrium....
and most classical board games including Go
Go (board game)
Go , is an ancient board game for two players that originated in China more than 2,000 years ago...
and chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
.
Many games studied by game theorists (including the famous prisoner's dilemma
Prisoner's dilemma
The prisoner’s dilemma is a canonical example of a game, analyzed in game theory that shows why two individuals might not cooperate, even if it appears that it is in their best interest to do so. It was originally framed by Merrill Flood and Melvin Dresher working at RAND in 1950. Albert W...
) are non-zero-sum games, because some outcomes
Outcome (Game theory)
In game theory, an outcome is a set of moves or strategies taken by the players, or their payoffs resulting from the actions or strategies taken by all players. The two are complementary in that, given knowledge of the set of strategies of all players, the final state of the game is known, as are...
have net results greater or less than zero. Informally, in non-zero-sum games, a gain by one player does not necessarily correspond with a loss by another.
Constant-sum games correspond to activities like theft and gambling, but not to the fundamental economic situation in which there are potential gains from trade
Gains from trade
Gains from trade in economics refers to net benefits to agents from allowing an increase in voluntary trading with each other. In technical terms, it is the increase of consumer surplus plus producer surplus from lower tariffs or otherwise liberalizing trade...
. It is possible to transform any game into a (possibly asymmetric) zero-sum game by adding an additional dummy player (often called "the board"), whose losses compensate the players' net winnings.
Simultaneous and sequential
Simultaneous gameSimultaneous game
In game theory, a simultaneous game is a game where each player chooses his action without knowledge of the actions chosen by other players. Normal form representations are usually used for simultaneous games....
s are games where both players move simultaneously, or if they do not move simultaneously, the later players are unaware of the earlier players' actions (making them effectively simultaneous). Sequential game
Sequential game
In game theory, a sequential game is a game where one player chooses his action before the others choose theirs. Importantly, the later players must have some information of the first's choice, otherwise the difference in time would have no strategic effect...
s (or dynamic games) are games where later players have some knowledge about earlier actions. This need not be perfect information
Perfect information
In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....
about every action of earlier players; it might be very little knowledge. For instance, a player may know that an earlier player did not perform one particular action, while he does not know which of the other available actions the first player actually performed.
The difference between simultaneous and sequential games is captured in the different representations discussed above. Often, normal form
Normal form game
In game theory, normal form is a way of describing a game. Unlike extensive form, normal-form representations are not graphical per se, but rather represent the game by way of a matrix. While this approach can be of greater use in identifying strictly dominated strategies and Nash equilibria, some...
is used to represent simultaneous games, and extensive form
Extensive form game
An extensive-form game is a specification of a game in game theory, allowing explicit representation of a number of important aspects, like the sequencing of players' possible moves, their choices at every decision point, the information each player has about the other player's moves when he...
is used to represent sequential ones. The transformation of extensive to normal form is one way, meaning that multiple extensive form games correspond to the same normal form. Consequently, notions of equilibrium for simultaneous games are insufficient for reasoning about sequential games; see subgame perfection.
Perfect information and imperfect information

Perfect information
In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....
. A game is one of perfect information if all players know the moves previously made by all other players. Thus, only sequential games can be games of perfect information, since in simultaneous games not every player knows the actions of the others. Most games studied in game theory are imperfect-information games, although there are some interesting examples of perfect-information games, including the ultimatum game
Ultimatum game
The ultimatum game is a game often played in economic experiments in which two players interact to decide how to divide a sum of money that is given to them. The first player proposes how to divide the sum between the two players, and the second player can either accept or reject this proposal. ...
and centipede game
Centipede game
In game theory, the centipede game, first introduced by Rosenthal , is an extensive form game in which two players take turns choosing either to take a slightly larger share of a slowly increasing pot, or to pass the pot to the other player...
. Recreational games of perfect information games include chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
, go
Go (board game)
Go , is an ancient board game for two players that originated in China more than 2,000 years ago...
, and mancala
Mancala
Mancala is a family of board games played around the world, sometimes called "sowing" games, or "count-and-capture" games, which describes the game-play. Mancala games play a role in many African and some Asian societies comparable to that of chess in the West, or the game of Go in Eastern Asia...
. Many card games are games of imperfect information, for instance poker
Poker
Poker is a family of card games that share betting rules and usually hand rankings. Poker games differ in how the cards are dealt, how hands may be formed, whether the high or low hand wins the pot in a showdown , limits on bet sizes, and how many rounds of betting are allowed.In most modern poker...
or contract bridge
Contract bridge
Contract bridge, usually known simply as bridge, is a trick-taking card game using a standard deck of 52 playing cards played by four players in two competing partnerships with partners sitting opposite each other around a small table...
.
Perfect information is often confused with complete information
Complete information
Complete information is a term used in economics and game theory to describe an economic situation or game in which knowledge about other market participants or players is available to all participants. Every player knows the payoffs and strategies available to other players.Complete information...
, which is a similar concept. Complete information requires that every player know the strategies and payoffs available to the other players but not necessarily the actions taken. Games of incomplete information can be reduced, however, to games of imperfect information by introducing "moves by nature
Move by nature
In game theory a move by nature is a decision or move in an extensive form game made by a player who has no strategic interests in the outcome. The effect is to add a player, 'Nature' whose practical role is to act as a random number generator...
" .
Combinatorial games
Games in which the difficulty of finding an optimal strategy stems from the multiplicity of possible moves are called combinatorial games. Examples include chess and go. Games that involve imperfect or incomplete information may also have a strong combinatorial character, for instance backgammonBackgammon
Backgammon is one of the oldest board games for two players. The playing pieces are moved according to the roll of dice, and players win by removing all of their pieces from the board. There are many variants of backgammon, most of which share common traits...
. There is no unified theory addressing combinatorial elements in games. There are, however, mathematical tools that can solve particular problems and answer some general questions.
Games of perfect information have been studied in combinatorial game theory
Combinatorial game theory
Combinatorial game theory is a branch of applied mathematics and theoretical computer science that studies sequential games with perfect information, that is, two-player games which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning...
, which has developed novel representations, e.g. surreal numbers, as well as combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and algebraic
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
(and sometimes non-constructive) proof methods to solve games
Solved game
A solved game is a game whose outcome can be correctly predicted from any position when each side plays optimally. Games which have not been solved are said to be "unsolved"...
of certain types, including some "loopy" games that may result in infinitely long sequences of moves. These methods address games with higher combinatorial complexity than those usually considered in traditional (or "economic") game theory. A typical game that has been solved this way is hex
Hex (board game)
Hex is a board game played on a hexagonal grid, theoretically of any size and several possible shapes, but traditionally as an 11x11 rhombus. Other popular dimensions are 13x13 and 19x19 as a result of the game's relationship to the older game of Go...
. A related field of study, drawing from computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, is game complexity
Game complexity
Combinatorial game theory has several ways of measuring game complexity. This article describes five of them: state-space complexity, game tree size, decision complexity, game-tree complexity, and computational complexity.-Measures of game complexity:...
, which is concerned with estimating the computational difficulty of finding optimal strategies.
Research in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
has addressed both perfect and imperfect (or incomplete) information games that have very complex combinatorial structures (like chess, go, or backgammon) for which no provable optimal strategies have been found. The practical solutions involve computational heuristics, like alpha-beta pruning
Alpha-beta pruning
Alpha-beta pruning is a search algorithm which seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player games...
or use of artificial neural network
Artificial neural network
An artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...
s trained by reinforcement learning
Reinforcement learning
Inspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
, which make games more tractable in computing practice.
Infinitely long games
Games, as studied by economists and real-world game players, are generally finished in finitely many moves. Pure mathematicians are not so constrained, and set theoristsSet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
in particular study games that last for infinitely many moves, with the winner (or other payoff) not known until after all those moves are completed.
The focus of attention is usually not so much on what is the best way to play such a game, but simply on whether one or the other player has a winning strategy. (It can be proven, using the axiom of choice, that there are games—even with perfect information, and where the only outcomes are "win" or "lose"—for which neither player has a winning strategy.) The existence of such strategies, for cleverly designed games, has important consequences in descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
.
Discrete and continuous games
Much of game theory is concerned with finite, discrete games, that have a finite number of players, moves, events, outcomes, etc. Many concepts can be extended, however. Continuous gameContinuous game
A continuous game is a mathematical generalization, used in game theory. It extends the notion of a discrete game, where the players choose from a finite set of pure strategies...
s allow players to choose a strategy from a continuous strategy set. For instance, Cournot competition
Cournot competition
Cournot competition is an economic model used to describe an industry structure in which companies compete on the amount of output they will produce, which they decide on independently of each other and at the same time. It is named after Antoine Augustin Cournot who was inspired by observing...
is typically modeled with players' strategies being any non-negative quantities, including fractional quantities.
Differential game
Differential game
In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. The problem usually consists of two actors, a pursuer and an evader, with conflicting goals...
s such as the continuous pursuit and evasion game
Pursuit-evasion
Pursuit-evasion is a family of problems in mathematics and computer science in which one group attempts to track down members of another group in an environment. Early work on problems of this type modeled the environment geometrically...
are continuous games.
Many-player and population games
Games with an arbitrary, but finite, number of players are often called n-person games . Evolutionary game theoryEvolutionary game theory
Evolutionary game theory is the application of Game Theory to evolving populations of lifeforms in biology. EGT is useful in this context by defining a framework of contests, strategies and analytics into which Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith...
considers games involving a population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
of decision makers, where the frequency with which a particular decision is made can change over time in response to the decisions made by all individuals in the population. In biology, this is intended to model (biological) evolution
Evolution
Evolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
, where genetically programmed organisms pass along some of their strategy programming to their offspring. In economics, the same theory is intended to capture population changes because people play the game many times within their lifetime, and consciously (and perhaps rationally) switch strategies .
Stochastic outcomes (and relation to other fields)
Individual decision problems with stochastic outcomes are sometimes considered "one-player games". These situations are not considered game theoretical by some authors. They may be modeled using similar tools within the related disciplines of decision theoryDecision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, and areas of artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, particularly AI planning (with uncertainty) and multi-agent system
Multi-agent system
A multi-agent system is a system composed of multiple interacting intelligent agents. Multi-agent systems can be used to solve problems that are difficult or impossible for an individual agent or a monolithic system to solve...
. Although these fields may have different motivators, the mathematics involved are substantially the same, e.g. using Markov decision process
Markov decision process
Markov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
es (MDP).
Stochastic outcomes can also be modeled in terms of game theory by adding a randomly acting player who makes "chance moves", also known as "moves by nature
Move by nature
In game theory a move by nature is a decision or move in an extensive form game made by a player who has no strategic interests in the outcome. The effect is to add a player, 'Nature' whose practical role is to act as a random number generator...
" . This player is not typically considered a third player in what is otherwise a two-player game, but merely serves to provide a roll of the dice where required by the game.
For some problems, different approaches to modeling stochastic outcomes may lead to different solutions. For example, the difference in approach between MDPs and the minimax solution
Minimax
Minimax is a decision rule used in decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. Alternatively, it can be thought of as maximizing the minimum gain...
is that the latter considers the worst-case over a set of adversarial moves, rather than reasoning in expectation about these moves given a fixed probability distribution. The minimax approach may be advantageous where stochastic models of uncertainty are not available, but may also be overestimating extremely unlikely (but costly) events, dramatically swaying the strategy in such scenarios if it is assumed that an adversary can force such an event to happen. (See black swan theory
Black swan theory
The black swan theory or theory of black swan events is a metaphor that encapsulates the concept that The event is a surprise and has a major impact...
for more discussion on this kind of modeling issue, particularly as it relates to predicting and limiting losses in investment banking.)
General models that include all elements of stochastic outcomes, adversaries, and partial or noisy observability (of moves by other players) have also been studied. The "gold standard
Gold standard
The gold standard is a monetary system in which the standard economic unit of account is a fixed mass of gold. There are distinct kinds of gold standard...
" is considered to be partially observable stochastic game
Stochastic game
In game theory, a stochastic game, introduced by Lloyd Shapley in the early 1950s, is a dynamic game with probabilistic transitions played by one or more players. The game is played in a sequence of stages. At the beginning of each stage the game is in some state...
(POSG), but few realistic problems are computationally feasible in POSG representation.
Metagames
These are games the play of which is the development of the rules for another game, the target or subject game. Metagames seek to maximize the utility value of the rule set developed. The theory of metagames is related to mechanism designMechanism design
Mechanism design is a field in game theory studying solution concepts for a class of private information games...
theory.
The term metagame analysis
Metagame analysis
Metagame analysis involves framing a problem situation as a strategic game in which participants try to realise their objectives by means of the options available to them...
is also used to refer to a practical approach developed by Nigel Howard whereby a situation is framed as a strategic game in which stakeholders try to realise their objectives by means of the options available to them. Subsequent developments have led to the formulation of drama theory.
See also
- Chainstore paradoxChainstore paradoxChainstore paradox is a concept that purports to refute standard game theory reasoning.-The chain store game:A monopolist has branches in 20 towns. He faces 20 potential competitors, one in each town, who will be able to choose IN or OUT. They do so in sequential order and one at a time...
- Combinatorial game theoryCombinatorial game theoryCombinatorial game theory is a branch of applied mathematics and theoretical computer science that studies sequential games with perfect information, that is, two-player games which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning...
- Glossary of game theory
- Intra-household bargainingIntra-household bargainingIntra-household bargaining refers to negotiations that occur between members of a household in order to arrive at decisions regarding the household unit....
- List of games in game theory
- Quantum game theoryQuantum game theoryQuantum game theory is an extension of classical game theory to the quantum domain. It differs from classical game theory in three primary ways:#Superposed initial states,#Quantum entanglement of initial states,...
- RationalityRationalityIn philosophy, rationality is the exercise of reason. It is the manner in which people derive conclusions when considering things deliberately. It also refers to the conformity of one's beliefs with one's reasons for belief, or with one's actions with one's reasons for action...
- Reverse Game TheoryMechanism designMechanism design is a field in game theory studying solution concepts for a class of private information games...
- Self-confirming equilibriumSelf-confirming equilibriumIn game theory, self-confirming equilibrium is a generalization of Nash equilibrium for extensive form games, in which players correctly predict the moves their opponents actually make, but may have misconceptions about what their opponents would do at information sets that are never reached when...
- Parrondo's paradoxParrondo's paradoxParrondo's paradox, a paradox in game theory, has been described as: A losing strategy that wins. It is named after its creator, Spanish physicist Juan Parrondo, who discovered the paradox in 1996...
Textbooks and general references
.- Aumann, Robert, and Sergiu HartSergiu HartSergiu Hart is an Israeli mathematician and economist and the past President of the Game Theory Society . He is the Kusiel-Vorreuter University Professor at the Center for the Study of Rationality at the Hebrew University of Jerusalem in Israel.Hart was born in Bucharest, Romania and immigrated to...
, ed. Handbook of Game Theory with Economic Applications scrollable to chapter-outline or abstract links:
- 1992. v. 1
- 1994. v. 2
- 2002. v. 3.
- The New Palgrave Dictionary of EconomicsThe New Palgrave Dictionary of EconomicsThe New Palgrave Dictionary of Economics , 2nd Edition, is an eight-volume reference work, edited by Steven N. Durlauf and Lawrence E. Blume. It contains 5.8 million words and spans 7,680 pages with 1,872 articles. Included are 1057 new articles and, from earlier, 80 essays that are designated as...
(2008). 2nd Edition:
- The New Palgrave Dictionary of Economics
- "game theory" by Robert J. Aumann. Abstract.
- "game theory in economics, origins of," by Robert Leonard. Abstract.
- "behavioural economics and game theory" by Faruk GulFaruk GülFaruk R. Gül is a Turkish American economist, a professor of economics at Princeton University and a Fellow of the Econometric Society.Gül did his undergraduate studies at Boğaziçi University, and received his Ph.D. from Princeton in 1986, where he was a student of Hugo F. Sonnenschein...
. Abstract. Description and Introduction, pp. 1–25.. Suitable for undergraduate and business students.. Suitable for upper-level undergraduates.. Acclaimed reference text. Description.. Suitable for advanced undergraduates.- Published in Europe as .. Presents game theory in formal way suitable for graduate level.. Snippets from interviews.. An 88-page mathematical introduction; free online at many universities.. Suitable for a general audience.. Undergraduate textbook.. Primer for business men and women.. A modern introduction at the graduate level.. A general history of game theory and game theoreticians.. A comprehensive reference from a computational perspective; downloadable free online. Praised primer and popular introduction for everybody, never out of print.
- Roger McCain's Game Theory: A Nontechnical Introduction to the Analysis of Strategy (Revised Edition)
- Christopher Griffin (2010) Game Theory: Penn State Math 486 Lecture Notes, pp. 169, CC-BY-NC-SA license, suitable introduction for undergraduates Consistent treatment of game types usually claimed by different applied fields, e.g. Markov decision processMarkov decision processMarkov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
es. - Joseph E. Harrington (2008) Games, strategies, and decision making, Worth, ISBN 0716766302. Textbook suitable for undergraduates in applied fields; numerous examples, fewer formalisms in concept presentation.
Historically important texts
- Aumann, R.J.Robert AumannRobert John Aumann is an Israeli-American mathematician and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem in Israel...
and Shapley, L.S.Lloyd ShapleyLloyd Stowell Shapley is a distinguished American mathematician and economist. He is a Professor Emeritus at University of California, Los Angeles, affiliated with departments of Mathematics and Economics...
(1974), Values of Non-Atomic Games, Princeton University Press
- reprinted edition:
- Shapley, L. S. (1953), A Value for n-person Games, In: Contributions to the Theory of Games volume II, H. W. Kuhn and A. W. Tucker (eds.)
- Shapley, L. S. (1953), Stochastic Games, Proceedings of National Academy of Science Vol. 39, pp. 1095–1100. English translation: "On the Theory of Games of Strategy," in A. W. Tucker and R. D. Luce, ed. (1959), Contributions to the Theory of Games, v. 4, p p. 13-42. Princeton University Press.
Other print references
- Allan GibbardAllan GibbardAllan Gibbard is the Richard B. Brandt Distinguished University Professor of Philosophy at the University of Michigan, Ann Arbor. Allan Gibbard has made several contributions to contemporary ethical theory, in particular metaethics...
, "Manipulation of voting schemes: a general result", Econometrica, Vol. 41, No. 4 (1973), pp. 587–601., ISBN 978-0-631-23257-5 (2002 edition). A layman's introduction.
- Mark A. Satterthwaite, "Strategy-proofness and Arrow's Conditions: Existence and Correspondence Theorems for Voting Procedures and Social Welfare Functions", Journal of Economic Theory 10 (April 1975), 187–217.
Websites
- Paul Walker: History of Game Theory Page.
- David Levine: Game Theory. Papers, Lecture Notes and much more stuff.
- Alvin Roth: Game Theory and Experimental Economics page - Comprehensive list of links to game theory information on the Web
- Adam Kalai: Game Theory and Computer Science - Lecture notes on Game Theory and Computer Science
- Mike Shor: Game Theory .net - Lecture notes, interactive illustrations and other information.
- Jim Ratliff's Graduate Course in Game Theory (lecture notes).
- Don Ross: Review Of Game Theory in the Stanford Encyclopedia of Philosophy.
- Bruno Verbeek and Christopher Morris: Game Theory and Ethics
- Elmer G. Wiens: Game Theory - Introduction, worked examples, play online two-person zero-sum games.
- Marek M. Kaminski: Game Theory and Politics - syllabuses and lecture notes for game theory and political science.
- Web sites on game theory and social interactions
- Kesten Green's Conflict Forecasting - See Papers for evidence on the accuracy of forecasts from game theory and other methods.
- McKelvey, Richard D., McLennan, Andrew M., and Turocy, Theodore L. (2007) Gambit: Software Tools for Game Theory.
- Benjamin Polak: Open Course on Game Theory at Yale videos of the course
- Benjamin Moritz, Bernhard Könsgen, Danny Bures, Ronni Wiersch, (2007) Spieltheorie-Software.de: An application for Game Theory implemented in JAVA.

