Computational complexity theory
Encyclopedia
Computational complexity theory is a branch of the theory of computation
in theoretical computer science
and mathematics
that focuses on classifying computational problems according to their inherent difficulty, and relating those classes
to each other. In this context, a computational problem is understood to be a task that is in principle amenable to being solved by a computer (which basically means that the problem can be stated by a set of mathematical instructions). Informally, a computational problem consists of problem instances and solutions to these problem instances. For example, primality testing is the problem of determining whether a given number is prime
or not. The instances of this problem are natural numbers, and the solution to an instance is yes or no based on whether the number is prime or not.
A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying the amount of resources needed to solve them, such as time and storage. Other complexity measures are also used, such as the amount of communication (used in communication complexity
), the number of gates
in a circuit (used in circuit complexity
) and the number of processors (used in parallel computing
). One of the roles of computational complexity theory is to determine the practical limits on what computer
s can and cannot do.
Closely related fields in theoretical computer science are analysis of algorithms
and computability theory
. A key distinction between analysis of algorithms and computational complexity theory is that the former is devoted to analyzing the amount of resources needed by a particular algorithm to solve a problem, whereas the latter asks a more general question about all possible algorithms that could be used to solve the same problem. More precisely, it tries to classify problems that can or cannot be solved with appropriately restricted resources. In turn, imposing restrictions on the available resources is what distinguishes computational complexity from computability theory: the latter theory asks what kind of problems can, in principle, be solved algorithmically.
can be viewed as an infinite collection of instances together with a solution for every instance. The input string for a computational problem is referred to as a problem instance, and should not be confused with the problem itself. In computational complexity theory, a problem refers to the abstract question to be solved. In contrast, an instance of this problem is a rather concrete utterance, which can serve as the input for a decision problem. For example, consider the problem of primality testing. The instance is a number (e.g. 15) and the solution is "yes" if the number is prime and "no" otherwise (in this case "no"). Alternatively, the instance is a particular input to the problem, and the solution is the output corresponding to the given input.
To further highlight the difference between a problem and an instance, consider the following instance of the decision version of the traveling salesman problem: Is there a route of at most 2000 kilometres in length passing through all of Germany's 15 largest cities? The answer to this particular problem instance is of little use for solving other instances of the problem, such as asking for a round trip through all sites in Milan
whose total length is at most 10 km. For this reason, complexity theory addresses computational problems and not particular problem instances.
over an alphabet. Usually, the alphabet is taken to be the binary alphabet (i.e., the set {0,1}), and thus the strings are bitstrings. As in a real-world computer, mathematical objects other than bitstrings must be suitably encoded. For example, integer
s can be represented in binary notation, and graphs
can be encoded directly via their adjacency matrices
, or by encoding their adjacency list
s in binary.
Even though some proofs of complexity-theoretic theorems regularly assume some concrete choice of input encoding, one tries to keep the discussion abstract enough to be independent of the choice of encoding. This can be achieved by ensuring that different representations can be transformed into each other efficiently.
s are one of the central objects of study in computational complexity theory. A decision problem is a special type of computational problem whose answer is either yes or no, or alternately either 1 or 0. A decision problem can be viewed as a formal language
, where the members of the language are instances whose answer is yes, and the non-members are those instances whose output is no. The objective is to decide, with the aid of an algorithm
, whether a given input string is a member of the formal language under consideration. If the algorithm deciding this problem returns the answer yes, the algorithm is said to accept the input string, otherwise it is said to reject the input.
An example of a decision problem is the following. The input is an arbitrary graph
. The problem consists in deciding whether the given graph is connected
, or not. The formal language associated with this decision problem is then the set of all connected graphs—of course, to obtain a precise definition of this language, one has to decide how graphs are encoded as binary strings.
is a computational problem where a single output (of a total function) is expected for every input, but the output is more complex than that of a decision problem
, that is, it isn't just yes or no. Notable examples include the traveling salesman problem and the integer factorization problem.
It is tempting to think that the notion of function problems is much richer than the notion of decision problems. However, this is not really the case, since function problems can be recast as decision problems. For example, the multiplication
of two integers can be expressed as the set of triples (a, b, c) such that the relation a × b = c holds. Deciding whether a given triple is member of this set corresponds to solving the problem of multiplying two numbers.
If the input size is n, the time taken can be expressed as a function of n. Since the time taken on different inputs of the same size can be different, the worst-case time complexity T(n) is defined to be the maximum time taken over all inputs of size n. If T(n) is a polynomial in n, then the algorithm is said to be a polynomial time algorithm. Cobham's thesis
says that a problem can be solved with a feasible amount of resources if it admits a polynomial time algorithm.
A Turing machine is a mathematical model of a general computing machine. It is a theoretical device that manipulates symbols contained on a strip of tape. Turing machines are not intended as a practical computing technology, but rather as a thought experiment representing a computing machine. It is believed that if a problem can be solved by an algorithm, there exists a Turing machine that solves the problem. Indeed, this is the statement of the Church–Turing thesis
. Furthermore, it is known that everything that can be computed on other models of computation known to us today, such as a RAM machine, Conway's Game of Life
, cellular automata or any programming language can be computed on a Turing machine. Since Turing machines are easy to analyze mathematically, and are believed to be as powerful as any other model of computation, the Turing machine is the most commonly used model in complexity theory.
Many types of Turing machines are used to define complexity classes, such as deterministic Turing machines, probabilistic Turing machine
s, non-deterministic Turing machine
s, quantum Turing machine
s, symmetric Turing machine
s and alternating Turing machine
s. They are all equally powerful in principle, but when resources (such as time or space) are bounded, some of these may be more powerful than others.
A deterministic Turing machine is the most basic Turing machine, which uses a fixed set of rules to determine its future actions. A probabilistic Turing machine is a deterministic Turing machine with an extra supply of random bits. The ability to make probabilistic decisions often helps algorithms solve problems more efficiently. Algorithms that use random bits are called randomized algorithm
s. A non-deterministic Turing machine is a deterministic Turing machine with an added feature of non-determinism, which allows a Turing machine to have multiple possible future actions from a given state. One way to view non-determinism is that the Turing machine branches into many possible computational paths at each step, and if it solves the problem in any of these branches, it is said to have solved the problem. Clearly, this model is not meant to be a physically realizable model, it is just a theoretically interesting abstract machine that gives rise to particularly interesting complexity classes. For examples, see nondeterministic algorithm
.
s. Perhaps surprisingly, each of these models can be converted to another without providing any extra computational power. The time and memory consumption of these alternate models may vary. What all these models have in common is that the machines operate deterministically
.
However, some computational problems are easier to analyze in terms of more unusual resources. For example, a nondeterministic Turing machine is a computational model that is allowed to branch out to check many different possibilities at once. The nondeterministic Turing machine has very little to do with how we physically want to compute algorithms, but its branching exactly captures many of the mathematical models we want to analyze, so that nondeterministic time is a very important resource in analyzing computational problems.
(f(n)).
Analogous definitions can be made for space requirements. Although time and space are the most well-known complexity resources, any complexity measure can be viewed as a computational resource. Complexity measures are very generally defined by the Blum complexity axioms. Other complexity measures used in complexity theory include communication complexity
, circuit complexity
, and decision tree complexity.
The best, worst and average case
complexity refer to three different ways of measuring the time complexity (or any other complexity measure) of different inputs of the same size. Since some inputs of size n may be faster to solve than others, we define the following complexities:
For example, consider the dc sorting algorithm quicksort. This solves the problem of sorting a list of integers that is given as the input. The worst-case is when the input is sorted or sorted in reverse order, and the algorithm takes time O(n2) for this case. If we assume that all possible permutations of the input list are equally likely, the average time taken for sorting is O(n log n). The best case occurs when each pivoting divides the list in half, also needing O(n log n) time.
. To show an upper bound T(n) on the time complexity of a problem, one needs to show only that there is a particular algorithm with running time at most T(n). However, proving lower bounds is much more difficult, since lower bounds make a statement about all possible algorithms that solve a given problem. The phrase "all possible algorithms" includes not just the algorithms known today, but any algorithm that might be discovered in the future. To show a lower bound of T(n) for a problem requires showing that no algorithm can have time complexity lower than T(n).
Upper and lower bounds are usually stated using the big Oh notation, which hides constant factors and smaller terms. This makes the bounds independent of the specific details of the computational model used. For instance, if T(n) = 7n2 + 15n + 40, in big Oh notation one would write T(n) = O(n2).
Of course, some complexity classes have complex definitions that do not fit into this framework. Thus, a typical complexity class has a definition like the following:
But bounding the computation time above by some concrete function f(n) often yields complexity classes that depend on the chosen machine model. For instance, the language {xx | x is any binary string} can be solved in linear time on a multi-tape Turing machine, but necessarily requires quadratic time in the model of single-tape Turing machines. If we allow polynomial variations in running time, Cobham-Edmonds thesis
states that "the time complexities in any two reasonable and general models of computation are polynomially related" . This forms the basis for the complexity class P
, which is the set of decision problems solvable by a deterministic Turing machine within polynomial time. The corresponding set of function problems is FP
.
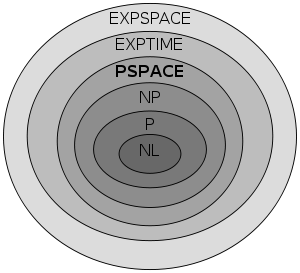Many important complexity classes can be defined by bounding the time or space used by the algorithm. Some important complexity classes of decision problems defined in this manner are the following:
It turns out that PSPACE = NPSPACE and EXPSPACE = NEXPSPACE by Savitch's theorem
.
Other important complexity classes include BPP, ZPP and RP
, which are defined using probabilistic Turing machine
s; AC
and NC
, which are defined using Boolean circuits and BQP
and QMA
, which are defined using quantum Turing machines. #P
is an important complexity class of counting problems (not decision problems). Classes like IP
and AM are defined using Interactive proof system
s. ALL
is the class of all decision problems.
More precisely, the time hierarchy theorem
states that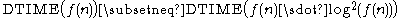
.
The space hierarchy theorem
states that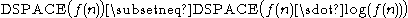
.
The time and space hierarchy theorems form the basis for most separation results of complexity classes. For instance, the time hierarchy theorem tells us that P is strictly contained in EXPTIME, and the space hierarchy theorem tells us that L is strictly contained in PSPACE.
s or log-space reduction
s.
The most commonly used reduction is a polynomial-time reduction. This means that the reduction process takes polynomial time. For example, the problem of squaring an integer can be reduced to the problem of multiplying two integers. This means an algorithm for multiplying two integers can be used to square an integer. Indeed, this can be done by giving the same input to both inputs of the multiplication algorithm. Thus we see that squaring is not more difficult than multiplication, since squaring can be reduced to multiplication.
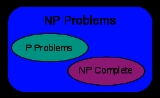
This motivates the concept of a problem being hard for a complexity class. A problem X is hard for a class of problems C if every problem in C can be reduced to X. Thus no problem in C is harder than X, since an algorithm for X allows us to solve any problem in C. Of course, the notion of hard problems depends on the type of reduction being used. For complexity classes larger than P, polynomial-time reductions are commonly used. In particular, the set of problems that are hard for NP is the set of NP-hard
problems.
If a problem X is in C and hard for C, then X is said to be complete
for C. This means that X is the hardest problem in C. (Since many problems could be equally hard, one might say that X is one of the hardest problems in C.) Thus the class of NP-complete
problems contains the most difficult problems in NP, in the sense that they are the ones most likely not to be in P. Because the problem P = NP is not solved, being able to reduce a known NP-complete problem, Π2, to another problem, Π1, would indicate that there is no known polynomial-time solution for Π1. This is because a polynomial-time solution to Π1 would yield a polynomial-time solution to Π2. Similarly, because all NP problems can be reduced to the set, finding an NP-complete
problem that can be solved in polynomial time would mean that P = NP.
, on the other hand, contains many problems that people would like to solve efficiently, but for which no efficient algorithm is known, such as the Boolean satisfiability problem
, the Hamiltonian path problem
and the vertex cover problem. Since deterministic Turing machines are special nondeterministic Turing machines, it is easily observed that each problem in P is also member of the class NP.
The question of whether P equals NP is one of the most important open questions in theoretical computer science because of the wide implications of a solution. If the answer is yes, many important problems can be shown to have more efficient solutions. These include various types of integer programming
problems in operations research
, many problems in logistics
, protein structure prediction
in biology
, and the ability to find formal proofs of pure mathematics
theorems. The P versus NP problem is one of the Millennium Prize Problems
proposed by the Clay Mathematics Institute
. There is a US$
1,000,000 prize for resolving the problem.
, the discrete logarithm problem and the integer factorization problem are examples of problems believed to be NP-intermediate. They are some of the very few NP problems not known to be in P or to be NP-complete.
The graph isomorphism problem
is the computational problem of determining whether two finite graph
s are isomorphic
. An important unsolved problem in complexity theory is whether the graph isomorphism problem is in P, NP-complete, or NP-intermediate. The answer is not known, but it is believed that the problem is at least not NP-complete. If graph isomorphism is NP-complete, the polynomial time hierarchy collapses to its second level. Since it is widely believed that the polynomial hierarchy does not collapse to any finite level, it is believed that graph isomorphism is not NP-complete. The best algorithm for this problem, due to Laszlo Babai
and Eugene Luks has run time 2O(√(n log(n))) for graphs with n vertices.
The integer factorization problem is the computational problem of determining the prime factorization of a given integer. Phrased as a decision problem, it is the problem of deciding whether the input has a factor less than k. No efficient integer factorization algorithm is known, and this fact forms the basis of several modern cryptographic systems, such as the RSA algorithm. The integer factorization problem is in NP and in co-NP (and even in UP and co-UP). If the problem is NP-complete, the polynomial time hierarchy will collapse to its first level (i.e., NP will equal co-NP). The best known algorithm for integer factorization is the general number field sieve
, which takes time O(e(64/9)1/3(n.log 2)1/3(log (n.log 2))2/3) to factor an n-bit integer. However, the best known quantum algorithm
for this problem, Shor's algorithm
, does run in polynomial time. Unfortunately, this fact doesn't say much about where the problem lies with respect to non-quantum complexity classes.
⊆ PSPACE, but it is possible that P = PSPACE. If P is not equal to NP, then P is not equal to PSPACE either. Since there are many known complexity classes between P and PSPACE, such as RP, BPP, PP, BQP, MA, PH, etc., it is possible that all these complexity classes collapse to one class. Proving that any of these classes are unequal would be a major breakthrough in complexity theory.
Along the same lines, co-NP is the class containing the complement
problems (i.e. problems with the yes/no answers reversed) of NP problems. It is believed that NP is not equal to co-NP; however, it has not yet been proven. It has been shown that if these two complexity classes are not equal then P is not equal to NP.
Similarly, it is not known if L (the set of all problems that can be solved in logarithmic space) is strictly contained in P or equal to P. Again, there are many complexity classes between the two, such as NL and NC, and it is not known if they are distinct or equal classes.
It is suspected that P and BPP are equal. However, it is currently open if BPP = NEXP.
Problems that can be solved in theory (e.g., given infinite time), but which in practice take too long for their solutions to be useful, are known as intractable problems. In complexity theory, problems that lack polynomial-time solutions are considered to be intractable for more than the smallest inputs. In fact, the Cobham–Edmonds thesis states that only those problems that can be solved in polynomial time can be feasibly computed on some computational device. Problems that are known to be intractable in this sense include those that are EXPTIME
-hard. If NP is not the same as P, then the NP-complete problems are also intractable in this sense. To see why exponential-time algorithms might be unusable in practice, consider a program that makes 2n operations before halting. For small n, say 100, and assuming for the sake of example that the computer does 1012 operations each second, the program would run for about 4 × 1010 years, which is roughly the age of the universe
. Even with a much faster computer, the program would only be useful for very small instances and in that sense the intractability of a problem is somewhat independent of technological progress. Nevertheless a polynomial time algorithm is not always practical. If its running time is, say, n15, it is unreasonable to consider it efficient and it is still useless except on small instances.
What intractability means in practice is open to debate. Saying that a problem is not in P does not imply that all large cases of the problem are hard or even that most of them are. For example the decision problem in Presburger arithmetic
has been shown not to be in P, yet algorithms have been written that solve the problem in reasonable times in most cases. Similarly, algorithms can solve the NP-complete knapsack problem
over a wide range of sizes in less than quadratic time and SAT solvers routinely handle large instances of the NP-complete Boolean satisfiability problem
.
. One approach to complexity theory of numerical analysis is information based complexity.
Continuous complexity theory can also refer to complexity theory of the use of analog computation, which uses continuous dynamical system
s and differential equation
s. Control theory
can be considered a form of computation and differential equations are used in the modelling of continuous-time and hybrid discrete-continuous-time systems.
in 1936, which turned out to be a very robust and flexible notion of computer.
date the beginning of systematic studies in computational complexity to the seminal paper "On the Computational Complexity of Algorithms" by Juris Hartmanis and Richard Stearns (1965), which laid out the definitions of time and space complexity and proved the hierarchy theorems.
According to , earlier papers studying problems solvable by Turing machines with specific bounded resources include John Myhill
's definition of linear bounded automata (Myhill 1960), Raymond Smullyan
's study of rudimentary sets (1961), as well as Hisao Yamada
's paper on real-time computations (1962). Somewhat earlier, Boris Trakhtenbrot
(1956), a pioneer in the field from the USSR, studied another specific complexity measure. As he remembers:
In 1967, Manuel Blum
developed an axiomatic complexity theory based on his axioms
and proved an important result, the so called, speed-up theorem
. The field really began to flourish when the US researcher Stephen Cook
and, working independently, Leonid Levin
in the USSR, proved that there exist practically relevant problems that are NP-complete
. In 1972, Richard Karp
took this idea a leap forward with his landmark paper, "Reducibility Among Combinatorial Problems", in which he showed that 21 diverse combinatorial
and graph theoretical
problems, each infamous for its computational intractability, are NP-complete.
Theory of computation
In theoretical computer science, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm...
in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
that focuses on classifying computational problems according to their inherent difficulty, and relating those classes
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
to each other. In this context, a computational problem is understood to be a task that is in principle amenable to being solved by a computer (which basically means that the problem can be stated by a set of mathematical instructions). Informally, a computational problem consists of problem instances and solutions to these problem instances. For example, primality testing is the problem of determining whether a given number is prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
or not. The instances of this problem are natural numbers, and the solution to an instance is yes or no based on whether the number is prime or not.
A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying the amount of resources needed to solve them, such as time and storage. Other complexity measures are also used, such as the amount of communication (used in communication complexity
Communication complexity
The notion of communication complexity was introduced by Yao in 1979,who investigated the following problem involving two separated parties . Alice receives an n-bit string x and Bob another n-bit string y, and the goal is for one of them to compute a certain function f with the least amount of...
), the number of gates
Logic gate
A logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and...
in a circuit (used in circuit complexity
Circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
) and the number of processors (used in parallel computing
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
). One of the roles of computational complexity theory is to determine the practical limits on what computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s can and cannot do.
Closely related fields in theoretical computer science are analysis of algorithms
Analysis of algorithms
To analyze an algorithm is to determine the amount of resources necessary to execute it. Most algorithms are designed to work with inputs of arbitrary length...
and computability theory
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
. A key distinction between analysis of algorithms and computational complexity theory is that the former is devoted to analyzing the amount of resources needed by a particular algorithm to solve a problem, whereas the latter asks a more general question about all possible algorithms that could be used to solve the same problem. More precisely, it tries to classify problems that can or cannot be solved with appropriately restricted resources. In turn, imposing restrictions on the available resources is what distinguishes computational complexity from computability theory: the latter theory asks what kind of problems can, in principle, be solved algorithmically.
Computational problems
Problem instances
A computational problemComputational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
can be viewed as an infinite collection of instances together with a solution for every instance. The input string for a computational problem is referred to as a problem instance, and should not be confused with the problem itself. In computational complexity theory, a problem refers to the abstract question to be solved. In contrast, an instance of this problem is a rather concrete utterance, which can serve as the input for a decision problem. For example, consider the problem of primality testing. The instance is a number (e.g. 15) and the solution is "yes" if the number is prime and "no" otherwise (in this case "no"). Alternatively, the instance is a particular input to the problem, and the solution is the output corresponding to the given input.
To further highlight the difference between a problem and an instance, consider the following instance of the decision version of the traveling salesman problem: Is there a route of at most 2000 kilometres in length passing through all of Germany's 15 largest cities? The answer to this particular problem instance is of little use for solving other instances of the problem, such as asking for a round trip through all sites in Milan
Milan
Milan is the second-largest city in Italy and the capital city of the region of Lombardy and of the province of Milan. The city proper has a population of about 1.3 million, while its urban area, roughly coinciding with its administrative province and the bordering Province of Monza and Brianza ,...
whose total length is at most 10 km. For this reason, complexity theory addresses computational problems and not particular problem instances.
Representing problem instances
When considering computational problems, a problem instance is a stringString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
over an alphabet. Usually, the alphabet is taken to be the binary alphabet (i.e., the set {0,1}), and thus the strings are bitstrings. As in a real-world computer, mathematical objects other than bitstrings must be suitably encoded. For example, integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s can be represented in binary notation, and graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
can be encoded directly via their adjacency matrices
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
, or by encoding their adjacency list
Adjacency list
In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node...
s in binary.
Even though some proofs of complexity-theoretic theorems regularly assume some concrete choice of input encoding, one tries to keep the discussion abstract enough to be independent of the choice of encoding. This can be achieved by ensuring that different representations can be transformed into each other efficiently.
Decision problems as formal languages
Decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s are one of the central objects of study in computational complexity theory. A decision problem is a special type of computational problem whose answer is either yes or no, or alternately either 1 or 0. A decision problem can be viewed as a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
, where the members of the language are instances whose answer is yes, and the non-members are those instances whose output is no. The objective is to decide, with the aid of an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, whether a given input string is a member of the formal language under consideration. If the algorithm deciding this problem returns the answer yes, the algorithm is said to accept the input string, otherwise it is said to reject the input.
An example of a decision problem is the following. The input is an arbitrary graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. The problem consists in deciding whether the given graph is connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
, or not. The formal language associated with this decision problem is then the set of all connected graphs—of course, to obtain a precise definition of this language, one has to decide how graphs are encoded as binary strings.
Function problems
A function problemFunction problem
In computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO...
is a computational problem where a single output (of a total function) is expected for every input, but the output is more complex than that of a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
, that is, it isn't just yes or no. Notable examples include the traveling salesman problem and the integer factorization problem.
It is tempting to think that the notion of function problems is much richer than the notion of decision problems. However, this is not really the case, since function problems can be recast as decision problems. For example, the multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of two integers can be expressed as the set of triples (a, b, c) such that the relation a × b = c holds. Deciding whether a given triple is member of this set corresponds to solving the problem of multiplying two numbers.
Measuring the size of an instance
To measure the difficulty of solving a computational problem, one may wish to see how much time the best algorithm requires to solve the problem. However, the running time may, in general, depend on the instance. In particular, larger instances will require more time to solve. Thus the time required to solve a problem (or the space required, or any measure of complexity) is calculated as function of the size of the instance. This is usually taken to be the size of the input in bits. Complexity theory is interested in how algorithms scale with an increase in the input size. For instance, in the problem of finding whether a graph is connected, how much more time does it take to solve a problem for a graph with 2n vertices compared to the time taken for a graph with n vertices?If the input size is n, the time taken can be expressed as a function of n. Since the time taken on different inputs of the same size can be different, the worst-case time complexity T(n) is defined to be the maximum time taken over all inputs of size n. If T(n) is a polynomial in n, then the algorithm is said to be a polynomial time algorithm. Cobham's thesis
Cobham's Thesis
Cobham's thesis, also known as Cobham–Edmonds thesis , asserts that computational problems can be feasibly computed on some computational device only if they can be computed in polynomial time; that is, if they lie in the complexity class P.Formally, to say that a problem can be solved in...
says that a problem can be solved with a feasible amount of resources if it admits a polynomial time algorithm.
Turing Machine
A Turing machine is a mathematical model of a general computing machine. It is a theoretical device that manipulates symbols contained on a strip of tape. Turing machines are not intended as a practical computing technology, but rather as a thought experiment representing a computing machine. It is believed that if a problem can be solved by an algorithm, there exists a Turing machine that solves the problem. Indeed, this is the statement of the Church–Turing thesis
Church–Turing thesis
In computability theory, the Church–Turing thesis is a combined hypothesis about the nature of functions whose values are effectively calculable; in more modern terms, algorithmically computable...
. Furthermore, it is known that everything that can be computed on other models of computation known to us today, such as a RAM machine, Conway's Game of Life
Conway's Game of Life
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
, cellular automata or any programming language can be computed on a Turing machine. Since Turing machines are easy to analyze mathematically, and are believed to be as powerful as any other model of computation, the Turing machine is the most commonly used model in complexity theory.
Many types of Turing machines are used to define complexity classes, such as deterministic Turing machines, probabilistic Turing machine
Probabilistic Turing machine
In computability theory, a probabilistic Turing machine is a non-deterministic Turing machine which randomly chooses between the available transitions at each point according to some probability distribution....
s, non-deterministic Turing machine
Non-deterministic Turing machine
In theoretical computer science, a Turing machine is a theoretical machine that is used in thought experiments to examine the abilities and limitations of computers....
s, quantum Turing machine
Quantum Turing machine
A quantum Turing machine , also a universal quantum computer, is an abstract machine used to model the effect of a quantum computer. It provides a very simple model which captures all of the power of quantum computation. Any quantum algorithm can be expressed formally as a particular quantum...
s, symmetric Turing machine
Symmetric Turing machine
- Definition of Symmetric Turing machines :A Symmetric TM is a TM which has a configuration graph that is undirected. That is configuration i yields configuration j if and only if j yields...
s and alternating Turing machine
Alternating Turing machine
In computational complexity theory, an alternating Turing machine is a non-deterministic Turing machine with a rule for accepting computations that generalizes the rules used in the definition of the complexity classes NP and co-NP...
s. They are all equally powerful in principle, but when resources (such as time or space) are bounded, some of these may be more powerful than others.
A deterministic Turing machine is the most basic Turing machine, which uses a fixed set of rules to determine its future actions. A probabilistic Turing machine is a deterministic Turing machine with an extra supply of random bits. The ability to make probabilistic decisions often helps algorithms solve problems more efficiently. Algorithms that use random bits are called randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s. A non-deterministic Turing machine is a deterministic Turing machine with an added feature of non-determinism, which allows a Turing machine to have multiple possible future actions from a given state. One way to view non-determinism is that the Turing machine branches into many possible computational paths at each step, and if it solves the problem in any of these branches, it is said to have solved the problem. Clearly, this model is not meant to be a physically realizable model, it is just a theoretically interesting abstract machine that gives rise to particularly interesting complexity classes. For examples, see nondeterministic algorithm
Nondeterministic algorithm
In computer science, a nondeterministic algorithm is an algorithm that can exhibit different behaviors on different runs, as opposed to a deterministic algorithm. There are several ways an algorithm may behave differently from run to run. A concurrent algorithm can perform differently on different...
.
Other machine models
Many machine models different from the standard multi-tape Turing machines have been proposed in the literature, for example random access machineRandom access machine
In computer science, random access machine is an abstract machine in the general class of register machines. The RAM is very similar to the counter machine but with the added capability of 'indirect addressing' of its registers...
s. Perhaps surprisingly, each of these models can be converted to another without providing any extra computational power. The time and memory consumption of these alternate models may vary. What all these models have in common is that the machines operate deterministically
Deterministic algorithm
In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...
.
However, some computational problems are easier to analyze in terms of more unusual resources. For example, a nondeterministic Turing machine is a computational model that is allowed to branch out to check many different possibilities at once. The nondeterministic Turing machine has very little to do with how we physically want to compute algorithms, but its branching exactly captures many of the mathematical models we want to analyze, so that nondeterministic time is a very important resource in analyzing computational problems.
Complexity measures
For a precise definition of what it means to solve a problem using a given amount of time and space, a computational model such as the deterministic Turing machine is used. The time required by a deterministic Turing machine M on input x is the total number of state transitions, or steps, the machine makes before it halts and outputs the answer ("yes" or "no"). A Turing machine M is said to operate within time f(n), if the time required by M on each input of length n is at most f(n). A decision problem A can be solved in time f(n) if there exists a Turing machine operating in time f(n) that solves the problem. Since complexity theory is interested in classifying problems based on their difficulty, one defines sets of problems based on some criteria. For instance, the set of problems solvable within time f(n) on a deterministic Turing machine is then denoted by DTIMEDTIME
In computational complexity theory, DTIME is the computational resource of computation time for a deterministic Turing machine. It represents the amount of time that a "normal" physical computer would take to solve a certain computational problem using a certain algorithm...
(f(n)).
Analogous definitions can be made for space requirements. Although time and space are the most well-known complexity resources, any complexity measure can be viewed as a computational resource. Complexity measures are very generally defined by the Blum complexity axioms. Other complexity measures used in complexity theory include communication complexity
Communication complexity
The notion of communication complexity was introduced by Yao in 1979,who investigated the following problem involving two separated parties . Alice receives an n-bit string x and Bob another n-bit string y, and the goal is for one of them to compute a certain function f with the least amount of...
, circuit complexity
Circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
, and decision tree complexity.
Best, worst and average case complexity
Best, worst and average case
In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively...
complexity refer to three different ways of measuring the time complexity (or any other complexity measure) of different inputs of the same size. Since some inputs of size n may be faster to solve than others, we define the following complexities:
- Best-case complexity: This is the complexity of solving the problem for the best input of size n.
- Worst-case complexity: This is the complexity of solving the problem for the worst input of size n.
- Average-case complexity: This is the complexity of solving the problem on an average. This complexity is only defined with respect to a probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
over the inputs. For instance, if all inputs of the same size are assumed to be equally likely to appear, the average case complexity can be defined with respect to the uniform distribution over all inputs of size n.
For example, consider the dc sorting algorithm quicksort. This solves the problem of sorting a list of integers that is given as the input. The worst-case is when the input is sorted or sorted in reverse order, and the algorithm takes time O(n2) for this case. If we assume that all possible permutations of the input list are equally likely, the average time taken for sorting is O(n log n). The best case occurs when each pivoting divides the list in half, also needing O(n log n) time.
Upper and lower bounds on the complexity of problems
To classify the computation time (or similar resources, such as space consumption), one is interested in proving upper and lower bounds on the minimum amount of time required by the most efficient algorithm solving a given problem. The complexity of an algorithm is usually taken to be its worst-case complexity, unless specified otherwise. Analyzing a particular algorithm falls under the field of analysis of algorithmsAnalysis of algorithms
To analyze an algorithm is to determine the amount of resources necessary to execute it. Most algorithms are designed to work with inputs of arbitrary length...
. To show an upper bound T(n) on the time complexity of a problem, one needs to show only that there is a particular algorithm with running time at most T(n). However, proving lower bounds is much more difficult, since lower bounds make a statement about all possible algorithms that solve a given problem. The phrase "all possible algorithms" includes not just the algorithms known today, but any algorithm that might be discovered in the future. To show a lower bound of T(n) for a problem requires showing that no algorithm can have time complexity lower than T(n).
Upper and lower bounds are usually stated using the big Oh notation, which hides constant factors and smaller terms. This makes the bounds independent of the specific details of the computational model used. For instance, if T(n) = 7n2 + 15n + 40, in big Oh notation one would write T(n) = O(n2).
Defining complexity classes
A complexity class is a set of problems of related complexity. Simpler complexity classes are defined by the following factors:- The type of computational problem: The most commonly used problems are decision problems. However, complexity classes can be defined based on function problemFunction problemIn computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO...
s, counting problems, optimization problemOptimization problemIn mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s, promise problemPromise problemIn computational complexity theory, a promise problem is a generalization of a decision problem where the input is promised to belong to a subset of all possible inputs. Unlike decision problems, the yes instances and no instances do not exhaust the set of all inputs...
s, etc. - The model of computation: The most common model of computation is the deterministic Turing machine, but many complexity classes are based on nondeterministic Turing machines, Boolean circuitBoolean circuitA Boolean circuit is a mathematical model of computation used in studying computational complexity theory. Boolean circuits are the main object of study in circuit complexity and are a special kind of circuits; a formal language can be decided by a family of Boolean circuits, one circuit for each...
s, quantum Turing machineQuantum Turing machineA quantum Turing machine , also a universal quantum computer, is an abstract machine used to model the effect of a quantum computer. It provides a very simple model which captures all of the power of quantum computation. Any quantum algorithm can be expressed formally as a particular quantum...
s, monotone circuits, etc. - The resource (or resources) that are being bounded and the bounds: These two properties are usually stated together, such as "polynomial time", "logarithmic space", "constant depth", etc.
Of course, some complexity classes have complex definitions that do not fit into this framework. Thus, a typical complexity class has a definition like the following:
- The set of decision problems solvable by a deterministic Turing machine within time f(n). (This complexity class is known as DTIME(f(n)).)
But bounding the computation time above by some concrete function f(n) often yields complexity classes that depend on the chosen machine model. For instance, the language {xx | x is any binary string} can be solved in linear time on a multi-tape Turing machine, but necessarily requires quadratic time in the model of single-tape Turing machines. If we allow polynomial variations in running time, Cobham-Edmonds thesis
Cobham's Thesis
Cobham's thesis, also known as Cobham–Edmonds thesis , asserts that computational problems can be feasibly computed on some computational device only if they can be computed in polynomial time; that is, if they lie in the complexity class P.Formally, to say that a problem can be solved in...
states that "the time complexities in any two reasonable and general models of computation are polynomially related" . This forms the basis for the complexity class P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, which is the set of decision problems solvable by a deterministic Turing machine within polynomial time. The corresponding set of function problems is FP
FP (complexity)
In computational complexity theory, the complexity class FP is the set of function problems which can be solved by a deterministic Turing machine in polynomial time; it is the function problem version of the decision problem class P...
.
Important complexity classes
| Complexity class | Model of computation | Resource constraint |
|---|---|---|
| DTIME DTIME In computational complexity theory, DTIME is the computational resource of computation time for a deterministic Turing machine. It represents the amount of time that a "normal" physical computer would take to solve a certain computational problem using a certain algorithm... (f(n)) |
Deterministic Turing machine | Time f(n) |
| P P (complexity) In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds... |
Deterministic Turing machine | Time poly(n) |
| EXPTIME EXPTIME In computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n.... |
Deterministic Turing machine | Time 2poly(n) |
| NTIME NTIME In computational complexity theory, the complexity class NTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O, and unlimited space.... (f(n)) |
Non-deterministic Turing machine | Time f(n) |
| NP NP (complexity) In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."... |
Non-deterministic Turing machine | Time poly(n) |
| NEXPTIME NEXPTIME In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O for some polynomial p, and unlimited space.... |
Non-deterministic Turing machine | Time 2poly(n) |
| DSPACE DSPACE In computational complexity theory, DSPACE or SPACE is the computational resource describing the resource of memory space for a deterministic Turing machine. It represents the total amount of memory space that a "normal" physical computer would need to solve a given computational problem with a... (f(n)) |
Deterministic Turing machine | Space f(n) |
| L L (complexity) In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space... |
Deterministic Turing machine | Space O(log n) |
| PSPACE PSPACE In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :... |
Deterministic Turing machine | Space poly(n) |
| EXPSPACE EXPSPACE In complexity theory, EXPSPACE is the set of all decision problems solvable by a deterministic Turing machine in O space, where p is a polynomial function of n... |
Deterministic Turing machine | Space 2poly(n) |
| NSPACE NSPACE In computational complexity theory, the complexity class NSPACE is the set of decision problems that can be solved by a non-deterministic Turing machine using space O, and unlimited time. It is the non-deterministic counterpart of DSPACE.Several important complexity classes can be defined in terms... (f(n)) |
Non-deterministic Turing machine | Space f(n) |
| NL NL (complexity) In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space.... |
Non-deterministic Turing machine | Space O(log n) |
| NPSPACE | Non-deterministic Turing machine | Space poly(n) |
| NEXPSPACE | Non-deterministic Turing machine | Space 2poly(n) |
It turns out that PSPACE = NPSPACE and EXPSPACE = NEXPSPACE by Savitch's theorem
Savitch's theorem
In computational complexity theory, Savitch's theorem, proved by Walter Savitch in 1970, states that for any function ƒ ≥ log,...
.
Other important complexity classes include BPP, ZPP and RP
RP (complexity)
In complexity theory, RP is the complexity class of problems for which a probabilistic Turing machine exists with these properties:* It always runs in polynomial time in the input size...
, which are defined using probabilistic Turing machine
Probabilistic Turing machine
In computability theory, a probabilistic Turing machine is a non-deterministic Turing machine which randomly chooses between the available transitions at each point according to some probability distribution....
s; AC
AC (complexity)
In circuit complexity, AC is a complexity class hierarchy. Each class, ACi, consists of the languages recognized by Boolean circuits with depth O and a polynomial number of unlimited-fanin AND and OR gates....
and NC
NC (complexity)
In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
, which are defined using Boolean circuits and BQP
BQP
In computational complexity theory BQP is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances...
and QMA
QMA
In computational complexity theory, QMA, which stands for Quantum Merlin Arthur, is the quantum analog of the deterministic complexity class NP or the probabilistic complexity class MA...
, which are defined using quantum Turing machines. #P
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
is an important complexity class of counting problems (not decision problems). Classes like IP
IP (complexity)
In computational complexity theory, the class IP is the class of problems solvable by an interactive proof system. The concept of an interactive proof system was first introduced by Shafi Goldwasser, Silvio Micali, and Charles Rackoff in 1985...
and AM are defined using Interactive proof system
Interactive proof system
In computational complexity theory, an interactive proof system is an abstract machine that models computation as the exchange of messages between two parties. The parties, the verifier and the prover, interact by exchanging messages in order to ascertain whether a given string belongs to a...
s. ALL
ALL (complexity)
In computability and complexity theory, ALL is the class of all decision problems.-Relations to other classes:ALL contains all complexity classes of decision problems, including RE and co-RE....
is the class of all decision problems.
Hierarchy theorems
For the complexity classes defined in this way, it is desirable to prove that relaxing the requirements on (say) computation time indeed defines a bigger set of problems. In particular, although DTIME(n) is contained in DTIME(n2), it would be interesting to know if the inclusion is strict. For time and space requirements, the answer to such questions is given by the time and space hierarchy theorems respectively. They are called hierarchy theorems because they induce a proper hierarchy on the classes defined by constraining the respective resources. Thus there are pairs of complexity classes such that one is properly included in the other. Having deduced such proper set inclusions, we can proceed to make quantitative statements about how much more additional time or space is needed in order to increase the number of problems that can be solved.More precisely, the time hierarchy theorem
Time hierarchy theorem
In computational complexity theory, the time hierarchy theorems are important statements about time-bounded computation on Turing machines. Informally, these theorems say that given more time, a Turing machine can solve more problems...
states that
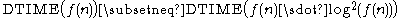.The space hierarchy theorem
Space hierarchy theorem
In computational complexity theory, the space hierarchy theorems are separation results that show that both deterministic and nondeterministic machines can solve more problems in more space, subject to certain conditions. For example, a deterministic Turing machine can solve more decision problems...
states that
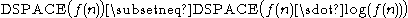.The time and space hierarchy theorems form the basis for most separation results of complexity classes. For instance, the time hierarchy theorem tells us that P is strictly contained in EXPTIME, and the space hierarchy theorem tells us that L is strictly contained in PSPACE.
Reduction
Many complexity classes are defined using the concept of a reduction. A reduction is a transformation of one problem into another problem. It captures the informal notion of a problem being at least as difficult as another problem. For instance, if a problem X can be solved using an algorithm for Y, X is no more difficult than Y, and we say that X reduces to Y. There are many different types of reductions, based on the method of reduction, such as Cook reductions, Karp reductions and Levin reductions, and the bound on the complexity of reductions, such as polynomial-time reductionPolynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
s or log-space reduction
Log-space reduction
In computational complexity theory, a log-space reduction is a reduction computable by a deterministic Turing machine using logarithmic space. Conceptually, this means it can keep a constant number of pointers into the input, along with a logarithmic number of fixed-size integers...
s.
The most commonly used reduction is a polynomial-time reduction. This means that the reduction process takes polynomial time. For example, the problem of squaring an integer can be reduced to the problem of multiplying two integers. This means an algorithm for multiplying two integers can be used to square an integer. Indeed, this can be done by giving the same input to both inputs of the multiplication algorithm. Thus we see that squaring is not more difficult than multiplication, since squaring can be reduced to multiplication.
This motivates the concept of a problem being hard for a complexity class. A problem X is hard for a class of problems C if every problem in C can be reduced to X. Thus no problem in C is harder than X, since an algorithm for X allows us to solve any problem in C. Of course, the notion of hard problems depends on the type of reduction being used. For complexity classes larger than P, polynomial-time reductions are commonly used. In particular, the set of problems that are hard for NP is the set of NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
problems.
If a problem X is in C and hard for C, then X is said to be complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
for C. This means that X is the hardest problem in C. (Since many problems could be equally hard, one might say that X is one of the hardest problems in C.) Thus the class of NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problems contains the most difficult problems in NP, in the sense that they are the ones most likely not to be in P. Because the problem P = NP is not solved, being able to reduce a known NP-complete problem, Π2, to another problem, Π1, would indicate that there is no known polynomial-time solution for Π1. This is because a polynomial-time solution to Π1 would yield a polynomial-time solution to Π2. Similarly, because all NP problems can be reduced to the set, finding an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem that can be solved in polynomial time would mean that P = NP.
Important open problems
P versus NP problem
The complexity class P is often seen as a mathematical abstraction modeling those computational tasks that admit an efficient algorithm. This hypothesis is called the Cobham–Edmonds thesis. The complexity class NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, on the other hand, contains many problems that people would like to solve efficiently, but for which no efficient algorithm is known, such as the Boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, the Hamiltonian path problem
Hamiltonian path problem
In the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph . Both problems are NP-complete...
and the vertex cover problem. Since deterministic Turing machines are special nondeterministic Turing machines, it is easily observed that each problem in P is also member of the class NP.
The question of whether P equals NP is one of the most important open questions in theoretical computer science because of the wide implications of a solution. If the answer is yes, many important problems can be shown to have more efficient solutions. These include various types of integer programming
Integer programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
problems in operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
, many problems in logistics
Logistics
Logistics is the management of the flow of goods between the point of origin and the point of destination in order to meet the requirements of customers or corporations. Logistics involves the integration of information, transportation, inventory, warehousing, material handling, and packaging, and...
, protein structure prediction
Protein structure prediction
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence — that is, the prediction of its secondary, tertiary, and quaternary structure from its primary structure. Structure prediction is fundamentally different from the inverse...
in biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, and the ability to find formal proofs of pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
theorems. The P versus NP problem is one of the Millennium Prize Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
proposed by the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
. There is a US$
United States dollar
The United States dollar , also referred to as the American dollar, is the official currency of the United States of America. It is divided into 100 smaller units called cents or pennies....
1,000,000 prize for resolving the problem.
Problems in NP not known to be in P or NP-complete
It was shown by Ladner that if P ≠ NP then there exist problems in NP that are neither in P nor NP-complete. Such problems are called NP-intermediate problems. The graph isomorphism problemGraph isomorphism problem
The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory as it is one of a very small number of problems belonging to NP...
, the discrete logarithm problem and the integer factorization problem are examples of problems believed to be NP-intermediate. They are some of the very few NP problems not known to be in P or to be NP-complete.
The graph isomorphism problem
Graph isomorphism problem
The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory as it is one of a very small number of problems belonging to NP...
is the computational problem of determining whether two finite graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s are isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
. An important unsolved problem in complexity theory is whether the graph isomorphism problem is in P, NP-complete, or NP-intermediate. The answer is not known, but it is believed that the problem is at least not NP-complete. If graph isomorphism is NP-complete, the polynomial time hierarchy collapses to its second level. Since it is widely believed that the polynomial hierarchy does not collapse to any finite level, it is believed that graph isomorphism is not NP-complete. The best algorithm for this problem, due to Laszlo Babai
László Babai
László Babai is a Hungarian professor of mathematics and computer science at the University of Chicago. His research focuses on computational complexity theory, algorithms, combinatorics, and finite groups, with an emphasis on the interactions between these fields...
and Eugene Luks has run time 2O(√(n log(n))) for graphs with n vertices.
The integer factorization problem is the computational problem of determining the prime factorization of a given integer. Phrased as a decision problem, it is the problem of deciding whether the input has a factor less than k. No efficient integer factorization algorithm is known, and this fact forms the basis of several modern cryptographic systems, such as the RSA algorithm. The integer factorization problem is in NP and in co-NP (and even in UP and co-UP). If the problem is NP-complete, the polynomial time hierarchy will collapse to its first level (i.e., NP will equal co-NP). The best known algorithm for integer factorization is the general number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
, which takes time O(e(64/9)1/3(n.log 2)1/3(log (n.log 2))2/3) to factor an n-bit integer. However, the best known quantum algorithm
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
for this problem, Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
, does run in polynomial time. Unfortunately, this fact doesn't say much about where the problem lies with respect to non-quantum complexity classes.
Separations between other complexity classes
Many known complexity classes are suspected to be unequal, but this has not been proved. For instance P ⊆ NP ⊆ PPPP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
⊆ PSPACE, but it is possible that P = PSPACE. If P is not equal to NP, then P is not equal to PSPACE either. Since there are many known complexity classes between P and PSPACE, such as RP, BPP, PP, BQP, MA, PH, etc., it is possible that all these complexity classes collapse to one class. Proving that any of these classes are unequal would be a major breakthrough in complexity theory.
Along the same lines, co-NP is the class containing the complement
Complement (complexity)
In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement...
problems (i.e. problems with the yes/no answers reversed) of NP problems. It is believed that NP is not equal to co-NP; however, it has not yet been proven. It has been shown that if these two complexity classes are not equal then P is not equal to NP.
Similarly, it is not known if L (the set of all problems that can be solved in logarithmic space) is strictly contained in P or equal to P. Again, there are many complexity classes between the two, such as NL and NC, and it is not known if they are distinct or equal classes.
It is suspected that P and BPP are equal. However, it is currently open if BPP = NEXP.
Intractability
Problems that can be solved in theory (e.g., given infinite time), but which in practice take too long for their solutions to be useful, are known as intractable problems. In complexity theory, problems that lack polynomial-time solutions are considered to be intractable for more than the smallest inputs. In fact, the Cobham–Edmonds thesis states that only those problems that can be solved in polynomial time can be feasibly computed on some computational device. Problems that are known to be intractable in this sense include those that are EXPTIME
EXPTIME
In computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
-hard. If NP is not the same as P, then the NP-complete problems are also intractable in this sense. To see why exponential-time algorithms might be unusable in practice, consider a program that makes 2n operations before halting. For small n, say 100, and assuming for the sake of example that the computer does 1012 operations each second, the program would run for about 4 × 1010 years, which is roughly the age of the universe
Age of the universe
The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...
. Even with a much faster computer, the program would only be useful for very small instances and in that sense the intractability of a problem is somewhat independent of technological progress. Nevertheless a polynomial time algorithm is not always practical. If its running time is, say, n15, it is unreasonable to consider it efficient and it is still useless except on small instances.
What intractability means in practice is open to debate. Saying that a problem is not in P does not imply that all large cases of the problem are hard or even that most of them are. For example the decision problem in Presburger arithmetic
Presburger arithmetic
Presburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
has been shown not to be in P, yet algorithms have been written that solve the problem in reasonable times in most cases. Similarly, algorithms can solve the NP-complete knapsack problem
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
over a wide range of sizes in less than quadratic time and SAT solvers routinely handle large instances of the NP-complete Boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
.
Continuous complexity theory
Continuous complexity theory can refer to complexity theory of problems that involve continuous functions that are approximated by discretizations, as studied in numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
. One approach to complexity theory of numerical analysis is information based complexity.
Continuous complexity theory can also refer to complexity theory of the use of analog computation, which uses continuous dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s and differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. Control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
can be considered a form of computation and differential equations are used in the modelling of continuous-time and hybrid discrete-continuous-time systems.
History
Before the actual research explicitly devoted to the complexity of algorithmic problems started off, numerous foundations were laid out by various researchers. Most influential among these was the definition of Turing machines by Alan TuringAlan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
in 1936, which turned out to be a very robust and flexible notion of computer.
date the beginning of systematic studies in computational complexity to the seminal paper "On the Computational Complexity of Algorithms" by Juris Hartmanis and Richard Stearns (1965), which laid out the definitions of time and space complexity and proved the hierarchy theorems.
According to , earlier papers studying problems solvable by Turing machines with specific bounded resources include John Myhill
John Myhill
John R. Myhill was a mathematician, born in 1923. He received his Ph.D. from Harvard University under Willard Van Orman Quine in 1949. He was professor at SUNY Buffalo from 1966 until his death in 1987...
's definition of linear bounded automata (Myhill 1960), Raymond Smullyan
Raymond Smullyan
Raymond Merrill Smullyan is an American mathematician, concert pianist, logician, Taoist philosopher, and magician.Born in Far Rockaway, New York, his first career was stage magic. He then earned a BSc from the University of Chicago in 1955 and his Ph.D. from Princeton University in 1959...
's study of rudimentary sets (1961), as well as Hisao Yamada
Hisao Yamada
-Selected publications:* Hisao Yamada: "A Historical Study of Typewriters and Typing Methods: from the Position of Planning Japanese Parallels", Journal of Information Processing, 2 , pp. 175–202-References:...
's paper on real-time computations (1962). Somewhat earlier, Boris Trakhtenbrot
Boris Trakhtenbrot
Boris Avraamovich Trakhtenbrot or Boaz Trakhtenbrot is an Israeli and Russian mathematician in mathematical logic, algorithms, theory of computation and cybernetics. He worked at Akademgorodok, Novosibirsk during the 1960s and 1970s...
(1956), a pioneer in the field from the USSR, studied another specific complexity measure. As he remembers:
In 1967, Manuel Blum
Manuel Blum
Manuel Blum is a computer scientist who received the Turing Award in 1995 "In recognition of his contributions to the foundations of computational complexity theory and its application to cryptography and program checking".-Biography:Blum attended MIT, where he received his bachelor's degree and...
developed an axiomatic complexity theory based on his axioms
Blum axioms
In computational complexity theory the Blum axioms or Blum complexity axioms are axioms which specify desirable properties of complexity measures on the set of computable functions. The axioms were first defined by Manuel Blum in 1967....
and proved an important result, the so called, speed-up theorem
Blum's speedup theorem
In computational complexity theory Blum's speedup theorem, first stated by Manuel Blum in 1967, is a fundamental theorem about the complexity of computable functions....
. The field really began to flourish when the US researcher Stephen Cook
Stephen Cook
Stephen Arthur Cook is a renowned American-Canadian computer scientist and mathematician who has made major contributions to the fields of complexity theory and proof complexity...
and, working independently, Leonid Levin
Leonid Levin
-External links:* at Boston University....
in the USSR, proved that there exist practically relevant problems that are NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. In 1972, Richard Karp
Richard Karp
Richard Manning Karp is a computer scientist and computational theorist at the University of California, Berkeley, notable for research in the theory of algorithms, for which he received a Turing Award in 1985, The Benjamin Franklin Medal in Computer and Cognitive Science in 2004, and the Kyoto...
took this idea a leap forward with his landmark paper, "Reducibility Among Combinatorial Problems", in which he showed that 21 diverse combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and graph theoretical
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
problems, each infamous for its computational intractability, are NP-complete.
See also
- List of computability and complexity topics
- List of important publications in theoretical computer science
- Unsolved problems in computer science
- :Category:Computational problems
- List of complexity classes
- Structural complexity theoryStructural complexity theoryIn computational complexity theory of computer science, the structural complexity theory or simply structural complexity is the study of complexity classes, rather than computational complexity of individual problems and algorithms...
- Descriptive complexity theory
- Quantum complexity theoryQuantum complexity theoryQuantum complexity theory is a part of computational complexity theory in theoretical computer science. It studies complexity classes defined using quantum computers and quantum information which are computational models based on quantum mechanics...
- Context of computational complexityContext of computational complexityIn computational complexity theory and analysis of algorithms, a number of metrics are defined describing the resources, such as time or space, that a machine needs to solve a particular problem. Interpreting these metrics meaningfully requires context, and this context is frequently implicit and...
- Parameterized ComplexityParameterized complexityParameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
- Game complexityGame complexityCombinatorial game theory has several ways of measuring game complexity. This article describes five of them: state-space complexity, game tree size, decision complexity, game-tree complexity, and computational complexity.-Measures of game complexity:...
- Proof complexityProof complexityIn computer science, proof complexity is a measure of efficiency of automated theorem proving methods that is based on the size of the proofs they produce. The methods for proving contradiction in propositional logic are the most analyzed...
- Transcomputational problemTranscomputational problemIn computational complexity theory, a transcomputational problem is a problem that requires processing of more than 1093 bits of information. Any number greater than 1093 is called a transcomputational number...