Brouwer fixed point theorem - AbsoluteAstronomy.com

Brouwer's fixed-point theorem is a fixed-point theorem

Fixed-point theorem

In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point , under some conditions on F that can be stated in general terms...

in topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, named after Luitzen Brouwer

Luitzen Egbertus Jan Brouwer

Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...

. It states that for any continuous function f with certain properties there is a point x₀ such that f(x₀) = x₀. The simplest form of Brouwer's theorem is for continuous functions f from a disk

Disk (mathematics)

In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...

D to itself. A more general form is for continuous functions from a convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

compact subset K of Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

to itself.

Among hundreds of fixed-point theorems, Brouwer's is particularly well known, due in part to its use across numerous fields of mathematics.
In its original field, this result is one of the key theorems characterizing the topology of Euclidean spaces, along with the Jordan curve theorem

Jordan curve theorem

In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...

, the hairy ball theorem

Hairy ball theorem

The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...

and the Borsuk–Ulam theorem

Borsuk–Ulam theorem

In mathematics, the Borsuk–Ulam theorem, named after Stanisław Ulam and Karol Borsuk, states that every continuous function from an n-sphere into Euclidean n-space maps some pair of antipodal points to the same point....

.
This gives it a place among the fundamental theorems of topology. The theorem is also used for proving deep results about differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

s and is covered in most introductory courses on differential geometry.
It appears in unlikely fields such as game theory

Game theory

Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...

. In economics, Brouwer's fixed-point theorem and its extension, the Kakutani fixed-point theorem, play a central role in the proof of existence of general equilibrium in market economies as developed in the 1950s by economics Nobel prize winners Gerard Debreu

Gerard Debreu

Gérard Debreu was a French economist and mathematician, who also came to have United States citizenship. Best known as a professor of economics at the University of California, Berkeley, where he began work in 1962, he won the 1983 Nobel Memorial Prize in Economics.-Biography:His father was the...

and Kenneth Arrow

Kenneth Arrow

Kenneth Joseph Arrow is an American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks in 1972. To date, he is the youngest person to have received this award, at 51....

.

The theorem was first studied in view of work on differential equations by the French mathematicians around Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

and Picard

Charles Émile Picard

Charles Émile Picard FRS was a French mathematician. He was elected the fifteenth member to occupy seat 1 of the Académie Française in 1924.- Biography :...

.
Proving results such as the Poincaré–Bendixson theorem

Poincaré–Bendixson theorem

In mathematics, the Poincaré–Bendixson theorem is a statement about the long-term behaviour of orbits of continuous dynamical systems on the plane.-Theorem:...

requires the use of topological methods.
This work at the end of the 19th century opened into several successive versions of the theorem. The general case was first proved in 1910 by Hadamard

Jacques Hadamard

Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...

, and then in 1912 by Luitzen Egbertus Jan Brouwer

Luitzen Egbertus Jan Brouwer

Statement

The theorem has several formulations, depending on the context in which it is used.
The simplest is sometimes given as follows:

In the plane: Every continuous function f from a closed

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

disk

Disk (mathematics)

In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...

to itself has at least one fixed point.

This can be generalized to an arbitrary finite dimension:

In Euclidean space:Every continuous function from a closed ball of a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

to itself has a fixed point.

A slightly more general version is as follows:

Convex compact set:Every continuous function f from a convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

subset K of a Euclidean space to K itself has a fixed point.

An even more general form is better known under a different name:

Schauder fixed point theorem

The Schauder fixed point theorem is an extension of the Brouwer fixed point theorem to topological vector spaces, which may be of infinite dimension...

:Every continuous function from a convex compact subset K of a Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

to K itself has a fixed point.

Illustrations

The theorem has several "real world" illustrations. For example: take two sheets of graph paper of equal size with coordinate systems on them, lay one flat on the table and crumple up (without ripping or tearing) the other one and place it, in any fashion, on top of the first so that the crumpled paper does not reach outside the flat one. There will then be at least one point of the crumpled sheet that lies directly above its corresponding point (i.e. the point with the same coordinates) of the flat sheet. This is a consequence of the n = 2 case of Brouwer's theorem applied to the continuous map that assigns to the coordinates of every point of the crumpled sheet the coordinates of the point of the flat sheet immediately beneath it.

Similarly: Take an ordinary map of a country, and suppose that that map is laid out on a table inside that country. There will always be a "You are Here" point on the map which represents that same point in the country.

In three dimensions the consequence of the Brouwer fixed-point theorem is that no matter how much you stir a cocktail in a glass some point in the liquid will remain in exactly the same place in the glass as before you took any action, assuming that, presumably, the final position of each point is a continuous function of its original position, and that the liquid after stirring is contained within the space originally taken up by it.

Explanations attributed to Brouwer

The theorem is supposed to have originated from Brouwer's observation of a cup of coffee.
If one stirs to dissolve a lump of sugar, it appears there is always a point without motion.
He drew the conclusion that at any moment, there is a point on the surface that is not moving.
The fixed point is not necessarily the point that seems to be motionless, since the centre of the turbulence moves a little bit.
The result is not intuitive, since the original fixed point may become mobile when another fixed point appears.

Brouwer is said to have added: "I can formulate this splendid result different, I take a horizontal sheet, and another identical one which I crumple, flatten and place on the other. Then a point of the crumpled sheet is in the same place as on the other sheet."
Brouwer "flattens" his sheet as with a flat iron, without removing the folds and wrinkles.

One-dimensional case

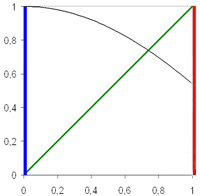
In one dimension, the result is intuitive and easy to prove. The continuous function f is defined on a closed interval [a, b] and takes values in the same interval. Saying that this function has a fixed point amounts to saying that its graph (black in the figure on the right) intersects that of the function defined on the same interval [a, b] which maps x to x (green).

Intuitively, any continuous line from the left edge of the square to the right edge must necessarily intersect the green diagonal.

It is not hard to give a formal proof. It suffices to consider the function g which maps x to f(x) - x. It is ≥ 0 on a and ≤ 0 on b. By the intermediate value theorem

Intermediate value theorem

In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....

, g has a zero in [a, b]; this zero is a fixed point.

Brouwer is said to have expressed this as follows: "Instead of examining a surface, we will prove the theorem about a piece of string. Let us begin with the string in an unfolded state, then refold it. Let us flatten the refolded string. Again a point of the string has not changed its position with respect to its original position on the unfolded string."

In one dimension, Brouwer's fixed point theorem is equivalent to the intermediate value theorem

Intermediate value theorem

History

The Brouwer fixed point theorem was one of the early achievements of algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

, and is the basis of more general fixed point theorems which are important in functional analysis

Functional analysis

Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...

. The case n = 3 first was proved by Piers Bohl

Piers Bohl

Piers Bohl was a Latvian mathematician, who worked in differential equations, topology and quasi-periodic functions....

in 1904 (published in Journal für die reine und angewandte Mathematik). It was later proved by L. E. J. Brouwer

Luitzen Egbertus Jan Brouwer

in 1909. Jacques Hadamard

Jacques Hadamard

Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...

proved the general case in 1910, and Brouwer found a different proof in 1912. Since these early proofs were all non-constructive

Constructive proof

In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...

indirect proofs, they ran contrary to Brouwer's intuitionist ideals. Methods to construct (approximations to) fixed points guaranteed by Brouwer's theorem are now known, however; see for example (Karamadian 1977) and (Istrăţescu 1981).

Prehistory

To understand the prehistory of Brouwer's fixed point theorem one needs to pass through differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

s. At the end of the 19th century, the old problem of the stability of the solar system

Stability of the Solar System

The stability of the Solar System is a subject of much inquiry in astronomy. Though the planets have been stable historically, and will be in the short term, their weak gravitational effects on one another can add up in unpredictable ways....

returned into the focus of the mathematical community.
Its solution required new methods. As noted by Henri Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

, who worked on the three-body problem

Three-body problem

Three-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...

, there is no hope to find an exact solution: "Nothing is more proper to give us an idea of the hardness of the three-body problem, and generally of all problems of Dynamics where there is no uniform integral and the Bohlin series diverge."
He also noted that the search for an approximate solution is no more efficient:
"the more we seek to obtain precise approximations, the more the result will diverge towards an increasing imprecision.".

He studied a question analogous to that of the surface movement in cup of coffee. What can we say, in general, about the trajectories on a surface animated by a constant flow

Flow (mathematics)

In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...

? Poincaré discovered that the answer can be found in what we now call the topological

Topology

properties in the area containing the trajectory. If this area is compact

Compact space

, i.e. both closed

Closed set

and bounded

Bounded set

In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...

, then the trajectory either becomes stationary, or it approaches a limit cycle. Poincaré went further; if the area is of the same kind as a disk, as is the case for the cup of coffee, there must necessarily be a fixed point. This fixed point is invariant under all functions which associate to each point of the original surface its position after a short time interval t. If the area is a circular band, or if it is not closed, then this is not necessarily the case.

To understand differential equations better, a new branch of mathematics was born. Poincaré called it analysis situs. The French Encyclopædia Universalis

Encyclopædia Universalis

The Encyclopædia Universalis is a French-language general encyclopedia published by Encyclopædia Britannica, Inc., a privately held company. The articles of the Encyclopædia Universalis are aimed at educated adult readers, and written by a staff of full-time editors and expert contributors...

defines it as the branch which "treats the properties of an object that are invariant if it is deformed in any continuous way, without tearing". In 1886, Poincaré proved a result that is equivalent to Brouwer's fixed-point theorem, although the connection with the subject of this article was not yet apparent. A little later, he developed one of the fundamental tools for better understanding the analysis situs, now known as the fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

or sometimes the Poincaré group. This method can be used for a very compact proof of the theorem under discussion.

Poincaré's method was analogous to that of Émile Picard, a contemporary mathematician who generalized the Cauchy–Lipschitz theorem. Picard's approach is based on a result that would later be formalised by another fixed-point theorem, named after Banach

Stefan Banach

Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....

. Instead of the topological properties of the domain, this theorem uses the fact that the function in question is a contraction

Contraction mapping

In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...

First proofs

At the dawn of the 20th century, the interest in analysis situs did not stay unnoticed. However, the necessity of a theorem equivalent to the one discussed in this article was not yet evident. Piers Bohl, a Latvian mathematician, applied topological methods to the study of differential equations. In 1904 he proved the three-dimensional case of our theorem, but his publication was not noticed.

It was Brouwer, finally, who gave the theorem its first patent of nobility. His goals were different from those of Poincaré. This mathematician was inspired by the foundations of mathematics, especially mathematical logic

Mathematical logic

Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...

and topology

Topology

. His initial interest lay in an attempt to solve Hilbert's fifth problem

Hilbert's fifth problem

Hilbert's fifth problem, is the fifth mathematical problem from the problem-list publicized in 1900 by mathematician David Hilbert, and concerns the characterization of Lie groups. The theory of Lie groups describes continuous symmetry in mathematics; its importance there and in theoretical physics...

. In 1909, during a voyage to Paris, he met Poincaré

Poincaré

Several members of the French Poincaré family have been successful in public and scientific life:* Henri Poincaré , physicist, mathematician and philosopher of science* Lucien Poincaré , physicist, brother of Raymond and cousin of Henri...

, Hadamard

Jacques Hadamard

Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...

and Borel

Émile Borel

Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...

. The ensuing discussions convinced Brouwer of the importance of a better understanding of Euclidean spaces, and were the origin of a fruitful exchange of letters with Hadamard. For the next four years, he concentrated on the proof of certain great theorems on this question. In 1912 he proved the hairy ball theorem

Hairy ball theorem

for the two-dimensional sphere, as well as the fact that every continuous map from the two-dimensional ball to itself has a fixed point. These two results in themselves were not really new. As Hadamard observed, Poincaré had shown a theorem equivalent to the hairy ball theorem. The revolutionary aspect of Brouwer's approach was his systematic use of recently developed tools such as homotopy

Homotopy

In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...

, the underlying concept of the Poincaré group. In the following year, Hadamard generalised the theorem under discussion to an arbitrary finite dimension, but he employed different methods. H. Freudenthal comments on the respective roles as follows: "Compared to Brouwer's revolutionary methods, those of Hadamard were very traditional, but Hadamard's participation in the birth of Brouwer's ideas resembles that of a midwife more than that of a mere spectator.".

Brouwer's approach yielded its fruits, and in 1912 he also found a proof that was valid for any finite dimension., as well as other key theorems such as the invariance of dimension. In the context of this work, Brouwer also generalized the Jordan curve theorem

Jordan curve theorem

In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...

to arbitrary dimension and established the properties connected with the degree of a continuous mapping

Degree of a continuous mapping

In topology, the degree is a numerical invariant that describes a continuous mapping between two compact oriented manifolds of the same dimension. Intuitively, the degree represents the number of times that the domain manifold wraps around the range manifold under the mapping...

. This branch of mathematics, originally envisioned by Poincaré and developed by Brouwer, changed its name. In the 1930s, analysis situs became algebraic topology

Algebraic topology

.

Brouwer's celebrity is not exclusively due to his topological work. He was also the originator and zealous defender of a way of formalising mathematics that is known as intuitionism

Intuitionistic logic

Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...

, which at the time made a stand against set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

. While Brouwer preferred constructive proof

Constructive proof

s, ironically, the original proofs of his great topological theorems were not constructive, and it took until 1967 for constructive proofs to be found.

Reception

The theorem proved its worth in more than one way. During the 20th century numerous fixed-point theorems were developed, and even a branch of mathematics called fixed-point theory.
Brouwer's theorem is probably the most important. It is also among the foundational theorems on the topology of topological manifold

Topological manifold

In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...

s and is often used to prove other important results such as the Jordan curve theorem

Jordan curve theorem

In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...

.

Besides the fixed-point theorems for more or less contracting

Contraction mapping

In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...

functions, there are many that have emerged directly or indirectly from the result under discussion. A continuous map from a closed ball of Euclidean space to its boundary cannot be the identity on the boundary. Similarly, the Borsuk–Ulam theorem

Borsuk–Ulam theorem

says that a continuous map from the n-dimensional sphere to Rⁿ has a pair of antipodal points that are mapped to the same point. In the finite-dimensional case, the Lefschetz fixed-point theorem

Lefschetz fixed-point theorem

In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X...

provided from 1926 a method for counting fixed points. In 1930, Brouwer's fixed-point theorem was generalized to Banach space

Banach space

s. This generalization is known as Schauder's fixed-point theorem, a result generalized further by S. Kakutani to multivalued function

Multivalued function

In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...

s. One also meets the theorem and its variants outside topology. It can be used to prove the Hartman-Grobman theorem

Hartman-Grobman theorem

In mathematics, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is an important theorem about the local behaviour of dynamical systems in the neighbourhood of a hyperbolic equilibrium point....

, which describes the qualitative behaviour of certain differential equations near certain equilibria. Similarly, Brouwer's theorem is used for the proof of the théorème de la variété centrale. The theorem can also be found in existence proofs for the solutions of certain partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

s.

Other areas are also touched. In game theory

Game theory

Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...

, John Nash

John Forbes Nash

John Forbes Nash, Jr. is an American mathematician whose works in game theory, differential geometry, and partial differential equations have provided insight into the forces that govern chance and events inside complex systems in daily life...

used the theorem to prove that in the game of Hex

Hex (board game)

Hex is a board game played on a hexagonal grid, theoretically of any size and several possible shapes, but traditionally as an 11x11 rhombus. Other popular dimensions are 13x13 and 19x19 as a result of the game's relationship to the older game of Go...

there is a winning strategy for white. In economy, P. Bich explains that certain generalizations of the theorem show that its use is helpful for certain classical problems in game theory and generally for equilibria (Hotelling's law

Hotelling's law

Hotelling's law is an observation in economics that in many markets it is rational for producers to make their products as similar as possible. This is also referred to as the principle of minimum differentiation as well as Hotelling's "linear city model"...

), financial equilibria and incomplete markets.

A proof using homology

The proof uses the observation that the boundary

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

of Dⁿ is S^n − 1, the (n − 1)-sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

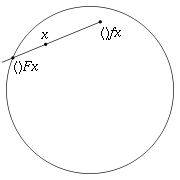
The argument proceeds by contradiction, supposing that a continuous function f : Dⁿ → Dⁿ has no fixed point, and then attempting to derive an inconsistency, which proves that the function must in fact have a fixed point. For each x in Dⁿ, there is only one straight line that passes through f(x) and x, because it must be the case that f(x) and x are distinct by hypothesis (recall that f having no fixed points means that f(x) ≠ x). Following this line from f(x) through x leads to a point on S^n − 1, denoted by F(x). This defines a continuous function F : Dⁿ → S^n − 1, which is a special type of continuous function known as a retraction: every point of the codomain

Codomain

In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...

(in this case S^n − 1) is a fixed point of the function.

Intuitively it seems unlikely that there could be a retraction of Dⁿ onto S^n − 1, and in the case n = 1 it is obviously impossible because S⁰ (i.e., the endpoints of the closed interval D¹) is not even connected. The case n = 2 is less obvious, but can be proven by using basic arguments involving the fundamental group

Fundamental group

s of the respective spaces: the retraction would induce an injective group homomorphism

Group homomorphism

In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...

from the fundamental group of S¹ to that of D², but the first group is isomorphic to Z while the latter group is trivial, so this is impossible. The case n = 2 can also be proven by contradiction based on a theorem about non-vanishing vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

s.

For n > 2, however, proving the impossibility of the retraction is more difficult. One way is to make use of homology groups

Homology (mathematics)

In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...

: the homology H_n − 1(Dⁿ) is trivial, while H_n − 1(S^n − 1) is infinite cyclic

Cyclic group

In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

. This shows that the retraction is impossible, because again the retraction would induce an injective group homomorphism from the latter to the former group.

A proof using Stokes's theorem

To prove that a map has fixed points, one can assume that it is smooth, because if a map has no fixed points then convoluting it with a smooth function of sufficiently small support produced a smooth function with no fixed points. As in the proof using homology, one is reduced to proving that there is no smooth retraction f from the ball B onto its boundary dB. If ω is a volume form on the boundary then

giving a contradiction.

More generally, this shows that there is no smooth retraction from any non-empty smooth orientable compact manifold onto its boundary. The proof using Stokes's theorem is closely related to the proof using homology (or rather cohomology), because the form ω generates the de Rham cohomology group Hⁿ⁻¹(dB) used in the cohomology proof.

A combinatorial proof

There is also a more elementary combinatorial proof

Combinatorial proof

In mathematics, the term combinatorial proof is often used to mean either of two types of proof of an identity in enumerative combinatorics that either states that two sets of combinatorial configurations, depending on one or more parameters, have the same number of elements , or gives a formula...

, whose main step consists in establishing Sperner's lemma

Sperner's lemma

In mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors...

in n dimensions.

A proof by Hirsch

There is also a quick proof, by Morris Hirsch

Morris Hirsch

Morris William Hirsch is an American mathematician, formerly at the University of California, Berkeley.A native of Chicago, Illinois, Hirsch attained his doctorate from the University of Chicago in 1958, under supervision of Edwin Spanier and Stephen Smale. His thesis was entitled Immersions of...

, based on the impossibility of a differentiable retraction. The indirect proof starts by noting that the map f can be approximated by a smooth map retaining the property of not fixing a point; this can be done by using the Weierstrass approximation theorem, for example. One then defines a retraction as above which must now be differentiable. Such a retraction must have a non-singular value, by Sard's theorem, which is also non-singular for the restriction to the boundary (which is just the identity). Thus the inverse image would be a 1-manifold with boundary. The boundary would have to contain at least two end points, both of which would have to lie on the boundary of the original ball—which is impossible in a retraction.

Kellogg, Li, and Yorke turned Hirsch's proof into a constructive proof by observing that the retract is in fact defined everywhere except at the fixed points. For almost any point, q, on the boundary, (assuming it is not a fixed point) the one manifold with boundary mentioned above does exist and the only possibility is that it leads from q to a fixed point. It is an easy numerical task to follow such a path from q to the fixed point so the method is essentially constructive. Chow, Mallet-Paret, and Yorke gave a conceptually similar path-following version of the homotopy proof which extends to a wide variety of related problems.

A proof using the game hex

A quite different proof given by David Gale

David Gale

David Gale was a distinguished American mathematician and economist. He was a Professor Emeritus at University of California, Berkeley, affiliated with departments of Mathematics, Economics, and Industrial Engineering and Operations Research...

is based on the game of Hex

Hex (board game)

. The basic theorem about Hex is that no game can end in a draw. This is equivalent to the Brouwer fixed-point theorem for dimension 2. By considering n-dimensional versions of Hex, one can prove in general that Brouwer's theorem is equivalent to the determinacy

Determinacy

In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...

theorem for Hex.

A proof using the Lefschetz fixed-point theorem

The Lefschetz fixed-point theorem says that if a continuous map f from a finite simplicial complex B to itself has only isolated fixed points, then the number of fixed points counted with multiplicities (which may be negative) is equal to the Lefschetz number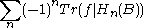

and in particular if the Lefschetz number is nonzero then f must have a fixed point. If B is a ball (or more generally is contractible) then the Lefschetz number is one because the only non-zero homology group is H⁰(B), so f has a fixed point.

A proof in a weak logical system

In reverse mathematics

Reverse mathematics

Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of...

, Brouwer's theorem can be proved in the system WKL₀, and conversely over the base system RCA₀

Reverse mathematics

Brouwer's theorem for a square implies the weak Konig's lemma, so this gives a precise description of the strength of Brouwer's theorem.

Generalizations

The Brouwer fixed-point theorem forms the starting point of a number of more general fixed-point theorem

Fixed-point theorem

In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point , under some conditions on F that can be stated in general terms...

s.

The straightforward generalization to infinite dimensions, i.e. using the unit ball of an arbitrary Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

instead of Euclidean space, is not true. The main problem here is that the unit balls of infinite-dimensional Hilbert spaces are not compact

Compact space

. For example, in the Hilbert space ℓ²

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

of square-summable real (or complex) sequences, consider the map f : ℓ² → ℓ² which sends a sequence (x_n) from the closed unit ball of ℓ² to the sequence (y_n) defined by

It is not difficult to check that this map is continuous, has its image in the unit sphere of ℓ², but does not have a fixed point.

The generalizations of the Brouwer fixed-point theorem to infinite dimensional spaces therefore all include a compactness assumption of some sort, and in addition also often an assumption of convexity

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

. See fixed-point theorems in infinite-dimensional spaces for a discussion of these theorems.

There is also finite-dimensional generalization to a larger class of spaces: If

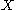is a product of finitely many chainable continua, then every continuous function

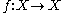has a fixed point, where a chainable continuum is a (usually but in this case not necessarily metric

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

) compact

Compact space

Hausdorff space

In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...

of which every open cover has a finite open refinement

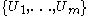, such that

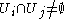if and only if

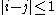. Examples of chainable continua include compact connected linearly ordered spaces and in particular closed intervals of real numbers.

The Kakutani fixed point theorem

Kakutani fixed point theorem

In mathematical analysis, the Kakutani fixed-point theorem is a fixed-point theorem for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex, compact subset of a Euclidean space to have a fixed point, i.e. a point which is mapped to a set containing...

generalizes the Brouwer fixed-point theorem in a different direction: it stays in Rⁿ, but considers upper semi-continuous correspondences

Correspondence (mathematics)

In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...

(functions that assign to each point of the set a subset of the set). It also requires compactness and convexity of the set.

The Lefschetz fixed-point theorem

Lefschetz fixed-point theorem

applies to (almost) arbitrary compact topological spaces, and gives a condition in terms of singular homology

Singular homology

In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....

that guarantees the existence of fixed points; this condition is trivially satisfied for any map in the case of Dⁿ.

External links

Brouwer's Fixed Point Theorem for Triangles at cut-the-knot
Cut-the-knot
Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
Brouwer theorem, from PlanetMath
PlanetMath
PlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...

with attached proof.
Reconstructing Brouwer at MathPages

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Statement

Illustrations

Explanations attributed to Brouwer

One-dimensional case

History

Prehistory

First proofs

Reception

A proof using homology

A proof using Stokes's theorem

A combinatorial proof

A proof by Hirsch

A proof using the game hex

A proof using the Lefschetz fixed-point theorem

A proof in a weak logical system

Generalizations

See also

External links