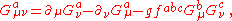Quantum chromodynamics
Encyclopedia
In theoretical physics
, quantum chromodynamics (QCD) is a theory of the strong interaction
(color
force), a fundamental force describing the interactions of the quark
s and gluon
s making up hadron
s (such as the proton
, neutron
or pion
). It is the study of the SU(3)
Yang–Mills theory of color-charged fermion
s (the quarks). QCD is a quantum field theory
of a special kind called a non-abelian gauge theory. It is an important part of the Standard Model
of particle physics
. A huge body of experimental evidence for QCD has been gathered over the years.
QCD enjoys two peculiar properties:
There is no known phase-transition line separating these two properties; confinement is dominant in low-energy scales but, as energy increases, asymptotic freedom becomes dominant.
(b. 1929) in its present sense. It originally comes from the phrase "Three quarks for Muster Mark" in Finnegans Wake
by James Joyce
. On June 27, 1978, Gell-Mann wrote a private letter to the editor of the Oxford English Dictionary, in which he related that he had been influenced by Joyce's words: "The allusion to three quarks seemed perfect." (Originally, only three quarks had been discovered.) Gell-Mann, however, wanted to pronounce the word with (ô) not (ä), as Joyce seemed to indicate by rhyming words in the vicinity such as Mark. Gell-Mann got around that "by supposing that one ingredient of the line 'Three quarks for Muster Mark' was a cry of 'Three quarts for Mister . . . ' heard in H.C. Earwicker's pub," a plausible suggestion given the complex punning in Joyce's novel.
The three kinds of charge
in QCD (as opposed to one in quantum electrodynamics
or QED) are usually referred to as "color charge
" by loose analogy to the three kinds of color
(red, green and blue) perceived by humans
. Other than this nomenclature, the quantum parameter "color" is completely unrelated to the everyday, familiar phenomenon of color.
Since the theory of electric charge is dubbed "electrodynamics", the Greek word "chroma" Χρώμα (meaning color) is applied to the theory of color charge, "chromodynamics".
s and spark chambers in the 1950s, experimental particle physics
discovered a large and ever-growing number of particles called hadron
s. It seemed that such a large number of particles could not all be fundamental. First, the particles were classified by charge
and isospin
by Eugene Wigner and Werner Heisenberg
; then, in 1953, according to strangeness by Murray Gell-Mann
and Kazuhiko Nishijima
. To gain greater insight, the hadrons were sorted into groups having similar properties and masses using the eightfold way
, invented in 1961 by Gell-Mann and Yuval Ne'eman
. Gell-Mann and George Zweig
, correcting an earlier approach of Shoichi Sakata
, went on to propose in 1963 that the structure of the groups could be explained by the existence of three flavor
s of smaller particles inside the hadrons: the quark
s.
Perhaps the first remark that quarks should possess an additional quantum number was made as a short footnote in the preprint of Boris Struminsky in connection with
hyperon composed of three strange quark
s with parallel spins (this situation was peculiar, because since quarks are fermion
s, such combination is forbidden by the Pauli exclusion principle
): Boris Struminsky was a PhD student of Nikolay Bogolyubov
. The problem considered in this preprint was suggested by Nikolay Bogolyubov, who advised Boris Struminsky in this research. In the beginning of 1965, Nikolay Bogolyubov
, Boris Struminsky and Albert Tavchelidze wrote a preprint with a more detailed discussion of the additional quark quantum degree of freedom. This work was also presented by Albert Tavchelidze without obtaining consent of his collaborators for doing so at an international conference in Trieste
(Italy
), in May 1965.
A similar mysterious situation was with the Δ++ baryon
; in the quark model, it is composed of three up quark
s with parallel spins. In 1965, Moo-Young Han
with Yoichiro Nambu
and Oscar W. Greenberg
independently resolved the problem by proposing that quarks possess an additional SU(3)
gauge
degree of freedom
, later called color charge. Han and Nambu noted that quarks might interact via an octet of vector gauge boson
s: the gluon
s.
Since free quark searches consistently failed to turn up any evidence for the new particles, and because an elementary particle back then was defined as a particle which could be separated and isolated, Gell-Mann often said that quarks were merely convenient mathematical constructs, not real particles. The meaning of this statement was usually clear in context: He meant quarks are confined, but he also was implying that the strong interactions could probably not be fully described by quantum field theory.
Richard Feynman
argued that high energy experiments showed quarks are real particles: he called them partons (since they were parts of hadrons). By particles, Feynman meant objects which travel along paths, elementary particles in a field theory.
The difference between Feynman's and Gell-Mann's approaches reflected a deep split in the theoretical physics community. Feynman thought the quarks have a distribution of position or momentum, like any other particle, and he (correctly) believed that the diffusion of parton momentum explained diffractive scattering
. Although Gell-Mann believed that certain quark charges could be localized, he was open to the possibility that the quarks themselves could not be localized because space and time break down. This was the more radical approach of S-matrix theory
.
James Bjorken proposed that pointlike partons would imply certain relations should hold in deep inelastic scattering
of electron
s and protons, which were spectacularly verified in experiments at SLAC in 1969. This led physicists to abandon the S-matrix approach for the strong interactions.
The discovery of asymptotic freedom
in the strong interactions by David Gross
, David Politzer and Frank Wilczek
allowed physicists to make precise predictions of the results of many high energy experiments using the quantum field theory technique of perturbation theory
. Evidence of gluons was discovered in three jet event
s at PETRA
in 1979. These experiments became more and more precise, culminating in the verification of perturbative QCD
at the level of a few percent at the LEP in CERN
.
The other side of asymptotic freedom is confinement. Since the force between color charges does not decrease with distance, it is believed that quarks and gluons can never be liberated from hadrons. This aspect of the theory is verified within lattice QCD
computations, but is not mathematically proven. One of the Millennium Prize Problems
announced by the Clay Mathematics Institute
requires a claimant to produce such a proof. Other aspects of non-perturbative QCD are the exploration of phases of quark matter
, including the quark-gluon plasma
.
The relation between the short-distance particle limit and the confining long-distance limit is one of the topics recently explored using string theory
, the modern form of S-matrix theory.
is based on certain symmetries of nature whose existence is deduced from observations. These can be
QCD is a gauge theory of the SU(3)
gauge group obtained by taking the color charge
to define a local symmetry.
Since the strong interaction does not discriminate between different flavors of quark, QCD has approximate flavor symmetry, which is broken by the differing masses of the quarks.
There are additional global symmetries whose definitions require the notion of chirality
, discrimination between left and right-handed. If the spin
of a particle has a positive projection
on its direction of motion then it is called left-handed; otherwise, it is right-handed. Chirality and handedness are not the same, but become approximately equivalent at high energies.
- to what one is used to, since usually one connects the absence of interactions with large distances. However, as already mentioned in the original paper of Franz Wegner, a solid state theorist who introduced 1971 simple gauge invariant lattice models, the high-temperature behaviour of the original model, e.g. the strong decay of correlations at large distances, corresponds to the low-temperature behaviour of the (usually ordered!) dual model, namely the asymptotic decay of non-trivial correlations, e.g. short-range deviations from almost perfect arrangements, for short distances. Here, in contrast to Wegner, we have only the dual model, which is that one described in this article.
: this is an abelian group
. If one considers a version of QCD with Nf flavors of massless quarks, then there is a global (chiral
) flavor symmetry group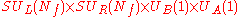
. The chiral symmetry is spontaneously broken
by the QCD vacuum
to the vector (L+R)
with the formation of a chiral condensate. The vector symmetry,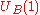 
corresponds to the baryon number of quarks and is an exact symmetry. The axial symmetry 
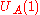is exact in the classical theory, but broken in the quantum theory, an occurrence called an anomaly
. Gluon field configurations called instanton
s are closely related to this anomaly.
There are two different types of SU(3) symmetry: there is the symmetry that acts on the different colors of quarks, and this is an exact gauge symmetry mediated by the gluons, and there is also a flavor symmetry which rotates different flavors of quarks to each other, or flavor SU(3). Flavor SU(3) is an approximate symmetry of the vacuum of QCD, and is not a fundamental symmetry at all. It is an accidental consequence of the small mass of the three lightest quarks.
In the QCD vacuum
there are vacuum condensates of all the quarks whose mass is less than the QCD scale. This includes the up and down quarks, and to a lesser extent the strange quark, but not any of the others. The vacuum is symmetric under SU(2) isospin
rotations of up and down, and to a lesser extent under rotations of up, down and strange, or full flavor group SU(3), and the observed particles make isospin and SU(3) multiplets.
The approximate flavor symmetries do have associated gauge bosons, observed particles like the rho and the omega, but these particles are nothing like the gluons and they are not massless. They are emergent gauge bosons in an approximate string description of QCD
.
is
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, quantum chromodynamics (QCD) is a theory of the strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
(color
Color charge
In particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
force), a fundamental force describing the interactions of the quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s and gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s making up hadron
Hadron
In particle physics, a hadron is a composite particle made of quarks held together by the strong force...
s (such as the proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
, neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
or pion
Pion
In particle physics, a pion is any of three subatomic particles: , , and . Pions are the lightest mesons and they play an important role in explaining the low-energy properties of the strong nuclear force....
). It is the study of the SU(3)
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
Yang–Mills theory of color-charged fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s (the quarks). QCD is a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of a special kind called a non-abelian gauge theory. It is an important part of the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
. A huge body of experimental evidence for QCD has been gathered over the years.
QCD enjoys two peculiar properties:
- Confinement, which means that the force between quarks does not diminish as they are separated. Because of this, it would take an infinite amount of energy to separate two quarks; they are forever bound into hadrons such as the protonProtonThe proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
and the neutronNeutronThe neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
. Although analytically unproven, confinement is widely believed to be true because it explains the consistent failure of free quark searches, and it is easy to demonstrate in lattice QCDLattice QCDLattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
. - Asymptotic freedomAsymptotic freedomIn physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
, which means that in very high-energy reactions, quarks and gluons interact very weakly. This prediction of QCD was first discovered in the early 1970s by David Politzer and by Frank WilczekFrank WilczekFrank Anthony Wilczek is a theoretical physicist from the United States and a Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology ....
and David GrossDavid GrossDavid Jonathan Gross is an American particle physicist and string theorist. Along with Frank Wilczek and David Politzer, he was awarded the 2004 Nobel Prize in Physics for their discovery of asymptotic freedom. He is currently the director and holder of the Frederick W...
. For this work they were awarded the 2004 Nobel Prize in PhysicsNobel Prize in PhysicsThe Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
.
There is no known phase-transition line separating these two properties; confinement is dominant in low-energy scales but, as energy increases, asymptotic freedom becomes dominant.
Terminology
The word quark was coined by American physicist Murray Gell-MannMurray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
(b. 1929) in its present sense. It originally comes from the phrase "Three quarks for Muster Mark" in Finnegans Wake
Finnegans Wake
Finnegans Wake is a novel by Irish author James Joyce, significant for its experimental style and resulting reputation as one of the most difficult works of fiction in the English language. Written in Paris over a period of seventeen years, and published in 1939, two years before the author's...
by James Joyce
James Joyce
James Augustine Aloysius Joyce was an Irish novelist and poet, considered to be one of the most influential writers in the modernist avant-garde of the early 20th century...
. On June 27, 1978, Gell-Mann wrote a private letter to the editor of the Oxford English Dictionary, in which he related that he had been influenced by Joyce's words: "The allusion to three quarks seemed perfect." (Originally, only three quarks had been discovered.) Gell-Mann, however, wanted to pronounce the word with (ô) not (ä), as Joyce seemed to indicate by rhyming words in the vicinity such as Mark. Gell-Mann got around that "by supposing that one ingredient of the line 'Three quarks for Muster Mark' was a cry of 'Three quarts for Mister . . . ' heard in H.C. Earwicker's pub," a plausible suggestion given the complex punning in Joyce's novel.
The three kinds of charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
in QCD (as opposed to one in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
or QED) are usually referred to as "color charge
Color charge
In particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
" by loose analogy to the three kinds of color
Color
Color or colour is the visual perceptual property corresponding in humans to the categories called red, green, blue and others. Color derives from the spectrum of light interacting in the eye with the spectral sensitivities of the light receptors...
(red, green and blue) perceived by humans
Color vision
Color vision is the capacity of an organism or machine to distinguish objects based on the wavelengths of the light they reflect, emit, or transmit...
. Other than this nomenclature, the quantum parameter "color" is completely unrelated to the everyday, familiar phenomenon of color.
Since the theory of electric charge is dubbed "electrodynamics", the Greek word "chroma" Χρώμα (meaning color) is applied to the theory of color charge, "chromodynamics".
History
With the invention of bubble chamberBubble chamber
A bubble chamber is a vessel filled with a superheated transparent liquid used to detect electrically charged particles moving through it. It was invented in 1952 by Donald A. Glaser, for which he was awarded the 1960 Nobel Prize in Physics...
s and spark chambers in the 1950s, experimental particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
discovered a large and ever-growing number of particles called hadron
Hadron
In particle physics, a hadron is a composite particle made of quarks held together by the strong force...
s. It seemed that such a large number of particles could not all be fundamental. First, the particles were classified by charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
and isospin
Isospin
In physics, and specifically, particle physics, isospin is a quantum number related to the strong interaction. This term was derived from isotopic spin, but the term is confusing as two isotopes of a nucleus have different numbers of nucleons; in contrast, rotations of isospin maintain the number...
by Eugene Wigner and Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
; then, in 1953, according to strangeness by Murray Gell-Mann
Murray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
and Kazuhiko Nishijima
Kazuhiko Nishijima
-Awards:*Nishina Memorial Prize*Japan Academy Prize*Order of Culture of Japan*Guggenheim Fellowship-Further reading:...
. To gain greater insight, the hadrons were sorted into groups having similar properties and masses using the eightfold way
Eightfold way (physics)
In physics, the Eightfold Way is a term coined by American physicist Murray Gell-Mann for a theory organizing subatomic baryons and mesons into octets...
, invented in 1961 by Gell-Mann and Yuval Ne'eman
Yuval Ne'eman
Yuval Ne'eman , was a renowned Israeli theoretical physicist, military scientist, and politician. He was a minister in the Israeli government in the 1980s and early 1990s.-Biography:...
. Gell-Mann and George Zweig
George Zweig
George Zweig was originally trained as a particle physicist under Richard Feynman and later turned his attention to neurobiology...
, correcting an earlier approach of Shoichi Sakata
Shoichi Sakata
was a Japanese academic and physicist who was internationally known for theoretical work on the structure of the atom. He proposed the Sakata model, which was an early precursor to the quark model....
, went on to propose in 1963 that the structure of the groups could be explained by the existence of three flavor
Flavour (particle physics)
In particle physics, flavour or flavor is a quantum number of elementary particles. In quantum chromodynamics, flavour is a global symmetry...
s of smaller particles inside the hadrons: the quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s.
Perhaps the first remark that quarks should possess an additional quantum number was made as a short footnote in the preprint of Boris Struminsky in connection with
hyperon composed of three strange quarkStrange quark
The strange quark or s quark is the third-lightest of all quarks, a type of elementary particle. Strange quarks are found in hadrons, which are subatomic particles. Example of hadrons containing strange quarks include kaons , strange D mesons , Sigma baryons , and other strange particles...
s with parallel spins (this situation was peculiar, because since quarks are fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s, such combination is forbidden by the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
): Boris Struminsky was a PhD student of Nikolay Bogolyubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
. The problem considered in this preprint was suggested by Nikolay Bogolyubov, who advised Boris Struminsky in this research. In the beginning of 1965, Nikolay Bogolyubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
, Boris Struminsky and Albert Tavchelidze wrote a preprint with a more detailed discussion of the additional quark quantum degree of freedom. This work was also presented by Albert Tavchelidze without obtaining consent of his collaborators for doing so at an international conference in Trieste
Trieste
Trieste is a city and seaport in northeastern Italy. It is situated towards the end of a narrow strip of land lying between the Adriatic Sea and Italy's border with Slovenia, which lies almost immediately south and east of the city...
(Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
), in May 1965.
A similar mysterious situation was with the Δ++ baryon
Delta baryon
The Delta baryons are a family of subatomic hadron particles which have the symbols , , , and and electric charges +2, +1, 0 and -1 elementary charge respectively...
; in the quark model, it is composed of three up quark
Up quark
The up quark or u quark is the lightest of all quarks, a type of elementary particle, and a major constituent of matter. It, along with the down quark, forms the neutrons and protons of atomic nuclei...
s with parallel spins. In 1965, Moo-Young Han
Moo-Young Han
Moo-Young Han is a professor of physics at Duke University. Along with Yoichiro Nambu of the University of Chicago, he is credited with introducing the SU symmetry of quarks, today known as the color charge...
with Yoichiro Nambu
Yoichiro Nambu
is a Japanese-born American physicist, currently a professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded a one-half share of the Nobel Prize in Physics in 2008 for the discovery of the mechanism of spontaneous broken symmetry in...
and Oscar W. Greenberg
Oscar W. Greenberg
Oscar Wallace Greenberg is an American physicist and professor at University of Maryland, College Park. He is famous for positing the existence of a property of subatomic particles called color charge.-Educational background:...
independently resolved the problem by proposing that quarks possess an additional SU(3)
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
gauge
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
degree of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
, later called color charge. Han and Nambu noted that quarks might interact via an octet of vector gauge boson
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s: the gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s.
Since free quark searches consistently failed to turn up any evidence for the new particles, and because an elementary particle back then was defined as a particle which could be separated and isolated, Gell-Mann often said that quarks were merely convenient mathematical constructs, not real particles. The meaning of this statement was usually clear in context: He meant quarks are confined, but he also was implying that the strong interactions could probably not be fully described by quantum field theory.
Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
argued that high energy experiments showed quarks are real particles: he called them partons (since they were parts of hadrons). By particles, Feynman meant objects which travel along paths, elementary particles in a field theory.
The difference between Feynman's and Gell-Mann's approaches reflected a deep split in the theoretical physics community. Feynman thought the quarks have a distribution of position or momentum, like any other particle, and he (correctly) believed that the diffusion of parton momentum explained diffractive scattering
Pomeron
In physics, the pomeron is a Regge trajectory, a family of particles with increasing spin, postulated in 1961 to explain the slowly rising cross section of hadronic collisions at high energies.-Overview:...
. Although Gell-Mann believed that certain quark charges could be localized, he was open to the possibility that the quarks themselves could not be localized because space and time break down. This was the more radical approach of S-matrix theory
S-matrix theory
S-matrix theory was a proposal for replacing local quantum field theory as the basic principle of elementary particle physics.It avoided the notion of space and time by replacing it with abstract mathematical properties of the S-matrix...
.
James Bjorken proposed that pointlike partons would imply certain relations should hold in deep inelastic scattering
Deep Inelastic Scattering
Deep inelastic scattering is the name given to a process used to probe the insides of hadrons , using electrons, muons and neutrinos. It provided the first convincing evidence of the reality of quarks, which up until that point had been considered by many to be a purely mathematical phenomenon...
of electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s and protons, which were spectacularly verified in experiments at SLAC in 1969. This led physicists to abandon the S-matrix approach for the strong interactions.
The discovery of asymptotic freedom
Asymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
in the strong interactions by David Gross
David Gross
David Jonathan Gross is an American particle physicist and string theorist. Along with Frank Wilczek and David Politzer, he was awarded the 2004 Nobel Prize in Physics for their discovery of asymptotic freedom. He is currently the director and holder of the Frederick W...
, David Politzer and Frank Wilczek
Frank Wilczek
Frank Anthony Wilczek is a theoretical physicist from the United States and a Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology ....
allowed physicists to make precise predictions of the results of many high energy experiments using the quantum field theory technique of perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
. Evidence of gluons was discovered in three jet event
Three jet event
In particle physics, a three-jet event is an event with many particles in final state that appear to be clustered in three jets. A single jet consists of particles that fly off in roughly the same direction. One can draw three cones from the interaction point, corresponding to the jets, and most...
s at PETRA
PETRA
PETRA is one of the particle accelerators at DESY in Hamburg, Germany. From 1978 to 1986 it was used to study electron–positron collisions. It was here that the TASSO collaboration found the first direct evidence for gluons in three jet events...
in 1979. These experiments became more and more precise, culminating in the verification of perturbative QCD
Perturbative QCD
Perturbative QCD is a subfield of particle physics in which the theory of strong interactions, Quantum Chromodynamics , is studied by using the fact that the strong coupling constant \alpha_s is small in high energy or short distance interactions, thus allowing Perturbation theory techniques to be...
at the level of a few percent at the LEP in CERN
CERN
The European Organization for Nuclear Research , known as CERN , is an international organization whose purpose is to operate the world's largest particle physics laboratory, which is situated in the northwest suburbs of Geneva on the Franco–Swiss border...
.
The other side of asymptotic freedom is confinement. Since the force between color charges does not decrease with distance, it is believed that quarks and gluons can never be liberated from hadrons. This aspect of the theory is verified within lattice QCD
Lattice QCD
Lattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
computations, but is not mathematically proven. One of the Millennium Prize Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
announced by the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
requires a claimant to produce such a proof. Other aspects of non-perturbative QCD are the exploration of phases of quark matter
QCD matter
Quark matter or QCD matter refers to any of a number of theorized phases of matter whose degrees of freedom include quarks and gluons. These theoretical phases would occur at extremely high temperatures and densities, billions of times higher than can be produced in equilibrium in laboratories...
, including the quark-gluon plasma
Quark-gluon plasma
A quark–gluon plasma or quark soup is a phase of quantum chromodynamics which exists at extremely high temperature and/or density. This phase consists of asymptotically free quarks and gluons, which are several of the basic building blocks of matter...
.
The relation between the short-distance particle limit and the confining long-distance limit is one of the topics recently explored using string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the modern form of S-matrix theory.
Theory
Some definitions
Every field theory of particle physicsParticle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
is based on certain symmetries of nature whose existence is deduced from observations. These can be
- local symmetriesLocal symmetryIn physics, a local symmetry is symmetry of some physical quantity, which smoothly depends on the point of the base manifold. Such quantities can be for example an observable, a tensor or the Lagrangian of a theory....
, that is the symmetry acts independently at each point in space-time. Each such symmetry is the basis of a gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
and requires the introduction of its own gauge bosonGauge bosonIn particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s. - global symmetriesGlobal symmetryA global symmetry is a symmetry that holds at all points in the spacetime under consideration, as opposed to a local symmetry which varies from point to point.Global symmetries require conservation laws, but not forces, in physics.-See also:...
, which are symmetries whose operations must be simultaneously applied to all points of space-time.
QCD is a gauge theory of the SU(3)
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
gauge group obtained by taking the color charge
Color charge
In particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
to define a local symmetry.
Since the strong interaction does not discriminate between different flavors of quark, QCD has approximate flavor symmetry, which is broken by the differing masses of the quarks.
There are additional global symmetries whose definitions require the notion of chirality
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
, discrimination between left and right-handed. If the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of a particle has a positive projection
Projection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
on its direction of motion then it is called left-handed; otherwise, it is right-handed. Chirality and handedness are not the same, but become approximately equivalent at high energies.
- Chiral symmetries involve independent transformations of these two types of particle.
- Vector symmetries (also called diagonal symmetries) mean the same transformation is applied on the two chiralities.
- Axial symmetries are those in which one transformation is applied on left-handed particles and the inverse on the right-handed particles.
Additional remarks: duality
As mentioned, asymptotic freedom means that at large energy - this corresponds also to short distances - there is practically no interaction between the particles. This is in contrast - more precisely one would say dualDualism
Dualism denotes a state of two parts. The term 'dualism' was originally coined to denote co-eternal binary opposition, a meaning that is preserved in metaphysical and philosophical duality discourse but has been diluted in general or common usages. Dualism can refer to moral dualism, Dualism (from...
- to what one is used to, since usually one connects the absence of interactions with large distances. However, as already mentioned in the original paper of Franz Wegner, a solid state theorist who introduced 1971 simple gauge invariant lattice models, the high-temperature behaviour of the original model, e.g. the strong decay of correlations at large distances, corresponds to the low-temperature behaviour of the (usually ordered!) dual model, namely the asymptotic decay of non-trivial correlations, e.g. short-range deviations from almost perfect arrangements, for short distances. Here, in contrast to Wegner, we have only the dual model, which is that one described in this article.
Symmetry groups
The color group SU(3) corresponds to the local symmetry whose gauging gives rise to QCD. The electric charge labels a representation of the local symmetry group U(1) which is gauged to give QEDQuantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
: this is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. If one considers a version of QCD with Nf flavors of massless quarks, then there is a global (chiral
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
) flavor symmetry group
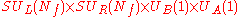. The chiral symmetry is spontaneously brokenSpontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
by the QCD vacuum
QCD vacuum
The QCD vacuum is the vacuum state of quantum chromodynamics . It is an example of a non-perturbative vacuum state, characterized by many non-vanishing condensates such as the gluon condensate or the quark condensate...
to the vector (L+R)
with the formation of a chiral condensate. The vector symmetry, 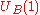corresponds to the baryon number of quarks and is an exact symmetry. The axial symmetry 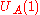is exact in the classical theory, but broken in the quantum theory, an occurrence called an anomalyAnomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics an anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking...
. Gluon field configurations called instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s are closely related to this anomaly.
There are two different types of SU(3) symmetry: there is the symmetry that acts on the different colors of quarks, and this is an exact gauge symmetry mediated by the gluons, and there is also a flavor symmetry which rotates different flavors of quarks to each other, or flavor SU(3). Flavor SU(3) is an approximate symmetry of the vacuum of QCD, and is not a fundamental symmetry at all. It is an accidental consequence of the small mass of the three lightest quarks.
In the QCD vacuum
QCD vacuum
The QCD vacuum is the vacuum state of quantum chromodynamics . It is an example of a non-perturbative vacuum state, characterized by many non-vanishing condensates such as the gluon condensate or the quark condensate...
there are vacuum condensates of all the quarks whose mass is less than the QCD scale. This includes the up and down quarks, and to a lesser extent the strange quark, but not any of the others. The vacuum is symmetric under SU(2) isospin
Isospin
In physics, and specifically, particle physics, isospin is a quantum number related to the strong interaction. This term was derived from isotopic spin, but the term is confusing as two isotopes of a nucleus have different numbers of nucleons; in contrast, rotations of isospin maintain the number...
rotations of up and down, and to a lesser extent under rotations of up, down and strange, or full flavor group SU(3), and the observed particles make isospin and SU(3) multiplets.
The approximate flavor symmetries do have associated gauge bosons, observed particles like the rho and the omega, but these particles are nothing like the gluons and they are not massless. They are emergent gauge bosons in an approximate string description of QCD
AdS/QCD
In theoretical physics, the AdS/QCD correspondence is a program to describe Quantum Chromodynamics in terms of a dual gravitational theory, following the principles of the AdS/CFT correspondence in a setup where the quantum field theory is not a conformal field theory.Such an alternative...
.
Lagrangian
The dynamics of the quarks and gluons are controlled by the quantum chromodynamics Lagrangian. The gauge invariant QCD LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
is
-
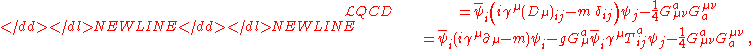
where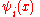
is the quark field, a dynamical function of space-time, in the fundamental representation of the SU(3) gauge groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, indexed by
; 
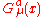are the gluon fields, also a dynamical function of space-time, in the adjoint representation of the SU(3) gauge group, indexed by 
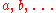. The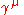 
are Dirac matrices connecting the spinor representation to the vector representation of the Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
; and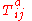
are the generators connecting the fundamental, antifundamental and adjoint representations of the SU(3) gauge group. The Gell-Mann matricesGell-Mann matricesThe Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....
provide one such representation for the generators.
The symbol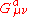
represents the gauge invariant gluonic field strength tensor, analogous to the electromagnetic field strength tensor, 
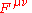, in Electrodynamics. It is given by
where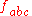
are the structure constants of SU(3). Note that the rules to move-up or pull-down the a, b, or c indexes are trivial, (+......+), so that 
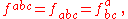whereas for the μ or ν indexes one has the non-trivial relativistic rules, corresponding e.g. to the signature (+---). Furthermore, for mathematicians, according to this formula the gluon color field can be represented by a SU(3)-Lie algebra-valued "curvature"-2-form 
where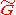 
is a "vector potential"-1-form corresponding to 
and 
is the (antisymmetric) "wedge productExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
" of this algebra, producing the "structure constants"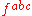
. The CartanCartanCartan may refer to:* Élie Cartan , French mathematician who worked with Lie groups* Henri Cartan , French mathematician who worked in algebraic topology, son of the above* Cartan , a lunar crater...
-derivative of the field form (i.e. essentially the divergence of the field) would be zero in the absence of the "gluon terms", i.e. those ~ g, which represent the non-abelian character of the SU(3).
The constants
and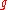 
control the quark mass and coupling constants of the theory, subject to renormalization in the full quantum theory.
An important theoretical notion concerning the final term of the above Lagrangian is the Wilson loopWilson loopIn gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
variable. This loop variable plays a most-important role in discretized forms of the QCD (see lattice QCDLattice QCDLattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
), and more generally, it distinguishes confinedConfinementConfinement may refer to either* Civil confinement for psychiatric patients* Color confinement, the physical principle explaining the non-observation of color charged particles like free quarks* Solitary confinement, a strict form of imprisonment...
and deconfined states of a gauge theory. It was introduced by the Nobel prizeNobel PrizeThe Nobel Prizes are annual international awards bestowed by Scandinavian committees in recognition of cultural and scientific advances. The will of the Swedish chemist Alfred Nobel, the inventor of dynamite, established the prizes in 1895...
winner Kenneth G. WilsonKenneth G. WilsonKenneth Geddes Wilson is an American theoretical physicist and Nobel Prize winner.As an undergraduate at Harvard, he was a Putnam Fellow. He earned his PhD from Caltech in 1961, studying under Murray Gell-Mann....
and is treated in a separate article.
Fields
Quarks are massive spin-1/2 fermionFermionIn particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s which carry a color chargeColor chargeIn particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
whose gauging is the content of QCD. Quarks are represented by Dirac fields in the fundamental representationFundamental representationIn representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
3 of the gauge group SU(3). They also carry electric charge (either -1/3 or 2/3) and participate in weak interactions as part of weak isospinWeak isospinIn particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
doublets. They carry global quantum numbers including the baryon number, which is 1/3 for each quark, hyperchargeHyperchargeIn particle physics, the hypercharge Y of a particle is related to the strong interaction, and is distinct from the similarly named weak hypercharge, which has an analogous role in the electroweak interaction...
and one of the flavor quantum numbers.
Gluons are spin-1 bosonBosonIn particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s which also carry color chargeColor chargeIn particle physics, color charge is a property of quarks and gluons that is related to the particles' strong interactions in the theory of quantum chromodynamics . Color charge has analogies with the notion of electric charge of particles, but because of the mathematical complications of QCD,...
s, since they lie in the adjoint representation 8 of SU(3). They have no electric charge, do not participate in the weak interactions, and have no flavor. They lie in the singlet representation 1 of all these symmetry groups.
Every quark has its own antiquark. The charge of each antiquark is exactly the opposite of the corresponding quark.
Dynamics
According to the rules of quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, and the associated Feynman diagramFeynman diagramFeynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s, the above theory gives rise to three basic interactions: a quark may emit (or absorb) a gluon, a gluon may emit (or absorb) a gluon, and two gluons may directly interact. This contrasts with QEDQuantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, in which only the first kind of interaction occurs, since photonPhotonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s have no charge. Diagrams involving Faddeev–Popov ghosts must be considered too.
Area law and confinement
Detailed computations with the above-mentioned Lagrangian show that the effective potential between a quark and its anti-quark in a mesonMesonIn particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
contains a term
, which represents some kind of "stiffness" of the interaction between the particle and its anti-particle at large
distances, similar to the entropic elasticityEntropic forceIn physics, an entropic force acting in a system is a phenomenological force resulting from the entire system's statistical tendency to increase its entropy, rather than from a particular underlying microscopic force.-Polymers:...
of a rubberRubberNatural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined...
band (see below). This leads to confinement of the quarks to the interior of hadrons, i.e. mesonMesonIn particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
s and nucleonNucleonIn physics, a nucleon is a collective name for two particles: the neutron and the proton. These are the two constituents of the atomic nucleus. Until the 1960s, the nucleons were thought to be elementary particles...
s, with typical radii Rc, corresponding to former "Bag models" of the hadrons . The order of magnitude of the "bag radius" is 1 fm (=10−15 m). Moreover, the above-mentioned stiffness is quantitatively related to the so-called "area law" behaviour of the expectation value of the Wilson loopWilson loopIn gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
product
of the ordered coupling constants around a closed loop W; i.e.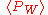 
is proportional to the area enclosed by the loop. For this behaviour the non-abelian behaviour of the gauge group is essential.
Methods
Further analysis of the content of the theory is complicated. Various techniques have been developed to work with QCD. Some of them are discussed briefly below.
Perturbative QCD
This approach is based on asymptotic freedom, which allows perturbation theoryPerturbation theory (quantum mechanics)In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
to be used accurately in experiments performed at very high energies. Although limited in scope, this approach has resulted in the most precise tests of QCD to date.
Lattice QCD
Among non-perturbative approaches to QCD, the most well established one is lattice QCDLattice QCDLattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
. This approach uses a discrete set of space-time points (called the lattice) to reduce the analytically intractable path integrals of the continuum theory to a very difficult numerical computation which is then carried out on supercomputers like the QCDOCQCDOCThe QCDOC, Quantum ChromoDynamics On a Chip, is a supercomputer technology focusing on using relatively cheap low power processing elements to produce a massively parallel machine...
which was constructed for precisely this purpose. While it is a slow and resource-intensive approach, it has wide applicability, giving insight into parts of the theory inaccessible by other means. However, the numerical sign problemNumerical sign problemThe numerical sign problem refers to the difficulty of numerically evaluating the integral of a highly oscillatory function of a large number of variables. Numerical methods fail because of the near-cancellation of the positive and negative contributions to the integral...
makes it difficult to use lattice methods to study QCD at high density and low temperature (e.g. nuclear matter or the interior of neutron stars).
1/N expansion
A well-known approximation scheme, the 1/N expansion1/N expansionIn quantum field theory and statistical mechanics, the 1/N expansion is a particular perturbative analysis of quantum field theories with an internal symmetry group such as SO or SU...
, starts from the premise that the number of colors is infinite, and makes a series of corrections to account for the fact that it is not. Until now it has been the source of qualitative insight rather than a method for quantitative predictions. Modern variants include the AdS/CFT approach.
Effective theories
For specific problems effective theories may be written down which give qualitatively correct results in certain limits. In the best of cases, these may then be obtained as systematic expansions in some parameter of the QCD Lagrangian. One such effective field theoryEffective field theoryIn physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
is chiral perturbation theoryChiral perturbation theoryChiral perturbation theory is an effective field theory constructed with a Lagrangian consistent with the chiral symmetry of quantum chromodynamics , as well as the other symmetries of parity and charge conjugation. ChPT is a theory which allows one to study the low-energy dynamics of QCD...
or ChiPT, which is the QCD effective theory at low energies. More precisely, it is a low energy expansion based on the spontaneous chiral symmetry breaking of QCD, which is an exact symmetry when quark masses are equal to zero, but for the u,d and s quark, which have small mass, it is still a good approximate symmetry. Depending on the number of quarks which are treated as light, one uses either SU(2) ChiPT or SU(3) ChiPT . Other effective theories are heavy quark effective theory (which expands around heavy quark mass near infinity), and soft-collinear effective theorySoft-collinear effective theoryIn quantum field theory, soft-collinear effective theory is a theoretical framework for doing calculations in quantum chromodynamics that involve interacting particles carrying widely different energies....
(which expands around large ratios of energy scales). In addition to effective theories, models like the Nambu-Jona-Lasinio modelNambu-Jona-Lasinio modelIn quantum field theory, the Nambu–Jona-Lasinio model is a theory of nucleons and mesons constructed from interacting Dirac fermions with chiral symmetry which parallels the construction of Cooper pairs from electrons in the BCS theory of superconductivity...
and the chiral modelChiral modelIn nuclear physics, the chiral model is a phenomenological model describing mesons in the chiral limit where the masses of the quarks go to zero . It's a nonlinear sigma model with the principal homogeneous space of the Lie group SU as its target manifold where N is the number of quark flavors...
are often used when discussing general features.
QCD Sum Rules
Based on an Operator product expansionOperator product expansion- 2D Euclidean quantum field theory :In quantum field theory, the operator product expansion is a Laurent series expansion of two operators...
one can derive sets of relations that connect different observables with each other.
Nambu-Jona-Lasinio model
A recent work by Kei-Ichi Kondo shows that the proper low-energy limit for QCD is a Nambu-Jona-Lasinio modelNambu-Jona-Lasinio modelIn quantum field theory, the Nambu–Jona-Lasinio model is a theory of nucleons and mesons constructed from interacting Dirac fermions with chiral symmetry which parallels the construction of Cooper pairs from electrons in the BCS theory of superconductivity...Nambu-Jona-Lasinio modelIn quantum field theory, the Nambu–Jona-Lasinio model is a theory of nucleons and mesons constructed from interacting Dirac fermions with chiral symmetry which parallels the construction of Cooper pairs from electrons in the BCS theory of superconductivity...
extended to a Polyakov-Nambu-Jona-Lasinio model at finite temperature.
Experimental tests
The notion of quark flavorsFlavour (particle physics)In particle physics, flavour or flavor is a quantum number of elementary particles. In quantum chromodynamics, flavour is a global symmetry...
was prompted by the necessity of explaining the properties of hadrons during the development of the quark modelQuark modelIn physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks which give rise to the quantum numbers of the hadrons....
. The notion of color was necessitated by the puzzle of the . This has been dealt with in the section on the history of QCD.
The first evidence for quarks as real constituent elements of hadrons was obtained in deep inelastic scatteringDeep Inelastic ScatteringDeep inelastic scattering is the name given to a process used to probe the insides of hadrons , using electrons, muons and neutrinos. It provided the first convincing evidence of the reality of quarks, which up until that point had been considered by many to be a purely mathematical phenomenon...
experiments at SLAC. The first evidence for gluons came in three jet eventThree jet eventIn particle physics, a three-jet event is an event with many particles in final state that appear to be clustered in three jets. A single jet consists of particles that fly off in roughly the same direction. One can draw three cones from the interaction point, corresponding to the jets, and most...
s at PETRAPETRAPETRA is one of the particle accelerators at DESY in Hamburg, Germany. From 1978 to 1986 it was used to study electron–positron collisions. It was here that the TASSO collaboration found the first direct evidence for gluons in three jet events...
.
Good quantitative tests of perturbative QCD are- the running of the QCD coupling as deduced from many observations
- scaling violation in polarized and unpolarized deep inelastic scatteringDeep Inelastic ScatteringDeep inelastic scattering is the name given to a process used to probe the insides of hadrons , using electrons, muons and neutrinos. It provided the first convincing evidence of the reality of quarks, which up until that point had been considered by many to be a purely mathematical phenomenon...
- vector bosonVector bosonIn particle physics, a vector boson is a boson with the spin quantum number equal to 1.The vector bosons considered to be elementary particles in the Standard Model are the gauge bosons or, the force carriers of fundamental interactions: the photon of electromagnetism, the W and Z bosons of the...
production at colliders (this includes the Drell-Yan processDrell-Yan processThe Drell–Yan process occurs in high energy hadron–hadron scattering. It takes place when a quark of one hadron and an antiquark of another hadron annihilate, creating a virtual photon or Z boson which then decays into a pair of oppositely-charged leptons...
) - jet cross sections in colliders
- event shape observables at the LEP
- heavy-quark production in colliders
Quantitative tests of non-perturbative QCD are fewer, because the predictions are harder to make. The best is probably the running of the QCD coupling as probed through latticeLattice QCDLattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
computations of heavy-quarkonium spectra. There is a recent claim about the mass of the heavy meson Bc http://www.aip.org/pnu/2005/split/731-1.html. Other non-perturbative tests are currently at the level of 5% at best. Continuing work on masses and form factorForm factorForm factor may refer to:*Form factor or emissivity, the proportion of energy transmitted by that object which can be transferred to another object...
s of hadrons and their weak matrix elements are promising candidates for future quantitative tests. The whole subject of quark matter and the quark-gluon plasmaQuark-gluon plasmaA quark–gluon plasma or quark soup is a phase of quantum chromodynamics which exists at extremely high temperature and/or density. This phase consists of asymptotically free quarks and gluons, which are several of the basic building blocks of matter...
is a non-perturbative test bed for QCD which still remains to be properly exploited.
Cross-relations to Solid State Physics
There are unexpected cross-relations to solid state physics. For example, the notion of gauge invariance forms the basis of the well-known Mattis spin glassSpin glassA spin glass is a magnet with frustrated interactions, augmented by stochastic disorder, where usually ferromagnetic and antiferromagnetic bonds are randomly distributed...
es, which are systems with the usual spin degrees of freedom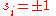
for i =1,...,N, with the special fixed "random" couplings 
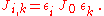Here the εi and εk quantities can independently and "randomly" take the values 
, which corresponds to a most-simple gauge transformation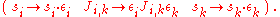 
This means that thermodynamic expectation values of measurable quantities, e.g. of the energy 
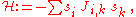are invariant.
However, here the coupling degrees of freedom
, which in the QCD correspond to the gluons, are "frozen" to fixed values (quenching). In contrast, in the QCD they "fluctuate" (annealing), and through the large number of gauge degrees of freedom the entropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
plays an important role (see below).
For positive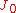
the thermodynamics of the Mattis spin glass corresponds in fact simply to a ferromagnet, just because these systems have no "frustrationGeometrical frustrationIn condensed matter physics, the term geometrical frustration means a phenomenon in which the geometrical properties of the crystal lattice or the presence of conflicting atomic forces forbid simultaneous minimization of the interaction energies acting at a given site.This may lead to highly...
“ at all. This term is a basic measure in spin glass theory. Quantitatively it is identical with the loop-product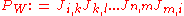
along a closed loop W. However, for a Mattis spin glass - in contrast to "genuine" spin glasses - the quantity PW never becomes negative.
The basic notion "frustration" of the spin-glass is actually similar to the Wilson loopWilson loopIn gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
quantity of the QCD. The only difference is again that in the QCD one is dealing with SU(3) matrices, and that one is dealing with a "fluctuating" quantity.
Energetically, perfect absence of frustration should be non-favorable and atypical for a spin glass, which means that one should add the loop-product to the Hamiltonian, by some kind of term representing a "punishment". - In the QCD the Wilson loop is essential for the Lagrangian rightaway.
The relation between the QCD and "disordered magnetic systems" (the spin glasses belong to them) were additionally stressed in a paper by Fradkin, Huberman und Shenker, which also stresses the notion of dualityDualismDualism denotes a state of two parts. The term 'dualism' was originally coined to denote co-eternal binary opposition, a meaning that is preserved in metaphysical and philosophical duality discourse but has been diluted in general or common usages. Dualism can refer to moral dualism, Dualism (from...
.
A further analogy consists in the already mentioned similarity to polymer physicsPolymer physicsPolymer physics is the field of physics that studies polymers, their fluctuations, mechanical properties, as well as the kinetics of reactions involving degradation and polymerisation of polymers and monomers respectively....
, where, analogously to Wilson LoopWilson loopIn gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
s, so-called "entangled nets" appear, which are important for the formation of the entropy-elasticityEntropic forceIn physics, an entropic force acting in a system is a phenomenological force resulting from the entire system's statistical tendency to increase its entropy, rather than from a particular underlying microscopic force.-Polymers:...
(force proportional to the length) of a rubber band. The non-abelian character of the SU(3) corresponds thereby to the non-trivial "chemical links“, which glue different loop segments together, and "asymptotic freedomAsymptotic freedomIn physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
" means in the polymer analogy simply the fact that in the short-wave limit, i.e. for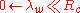
(where Rc is a characteristic correlation-length for the glued loops, corresponding to the above-mentioned "bag radius", while λw is the wavelength of an excitation) any non-trivial correlation vanishes totally, as if the system had crystallized.
There is also a correspondence between confinement in QCD - the fact that the color-field is only different from zero in the interior of hadrons - and the behaviour of the usual magnetic field in the theory of type-II superconductorType-II superconductorA Type-II superconductor is a superconductor characterized by the formation of vortex lattices in magnetic field. It has a continuous second order phase transition from the superconducting to the normal state within an increasing magnetic field....
s: there the magnetism is confined to the interiour of the Abrikosov flux-line latticeAbrikosov vortexIn superconductivity, an Abrikosov vortex is a vortex of supercurrent in a type-II superconductor. The supercurrent circulates around the normal core of the vortex. The core has a size \sim\xi — the superconducting coherence length...
, i.e., the London penetration depth λ of that theory is analogous to the confinement radius Rc of quantum chromodynamics. Mathematically, this correspondendence is supported by the second term,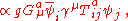
on the r.h.s. of the Lagrangian.
See also
- For overviews, see Standard ModelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, its field theoretical formulationStandard model (basic details)This is a detailed description of the standard model of particle physics. It describes how the leptons, quarks, gauge bosons and the Higgs particle fit together...
, strong interactionStrong interactionIn particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
s, quarkQuarkA quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s and gluonGluonGluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s, hadronHadronIn particle physics, a hadron is a composite particle made of quarks held together by the strong force...
s, confinementColour confinementColor confinement, often simply called confinement, is the physics phenomenon that color charged particles cannot be isolated singularly, and therefore cannot be directly observed. Quarks, by default, clump together to form groups, or hadrons. The two types of hadrons are the mesons and the baryons...
, QCD matterQCD matterQuark matter or QCD matter refers to any of a number of theorized phases of matter whose degrees of freedom include quarks and gluons. These theoretical phases would occur at extremely high temperatures and densities, billions of times higher than can be produced in equilibrium in laboratories...
, or quark-gluon plasmaQuark-gluon plasmaA quark–gluon plasma or quark soup is a phase of quantum chromodynamics which exists at extremely high temperature and/or density. This phase consists of asymptotically free quarks and gluons, which are several of the basic building blocks of matter...
. - For details, see gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, quantization procedureQuantum gauge theoryIn quantum physics, in order to quantize a gauge theory, like for example Yang-Mills theory, Chern-Simons or BF model, one method is to perform a gauge fixing. This is done in the BRST and Batalin-Vilkovisky formulation...
including BRST quantizationBRST quantizationIn theoretical physics, BRST quantization is a relatively rigorous mathematical approach to quantizing a field theory with a gauge symmetry...
and Faddeev–Popov ghosts. A more general category is quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. - For techniques, see Lattice QCDLattice QCDLattice QCD is a well-established non-perturbative approach to solving the quantum chromodynamics theory of quarks and gluons. It is a lattice gauge theory formulated on a grid or lattice of points in space and time....
, 1/N expansion1/N expansionIn quantum field theory and statistical mechanics, the 1/N expansion is a particular perturbative analysis of quantum field theories with an internal symmetry group such as SO or SU...
, perturbative QCDPerturbative QCDPerturbative QCD is a subfield of particle physics in which the theory of strong interactions, Quantum Chromodynamics , is studied by using the fact that the strong coupling constant \alpha_s is small in high energy or short distance interactions, thus allowing Perturbation theory techniques to be...
, Soft-collinear effective theorySoft-collinear effective theoryIn quantum field theory, soft-collinear effective theory is a theoretical framework for doing calculations in quantum chromodynamics that involve interacting particles carrying widely different energies....
, heavy quark effective theory, chiral modelChiral modelIn nuclear physics, the chiral model is a phenomenological model describing mesons in the chiral limit where the masses of the quarks go to zero . It's a nonlinear sigma model with the principal homogeneous space of the Lie group SU as its target manifold where N is the number of quark flavors...
s, and the Nambu and Jona-Lasinio modelNambu-Jona-Lasinio modelIn quantum field theory, the Nambu–Jona-Lasinio model is a theory of nucleons and mesons constructed from interacting Dirac fermions with chiral symmetry which parallels the construction of Cooper pairs from electrons in the BCS theory of superconductivity...
. - For experiments, see quark search experiments, deep inelastic scatteringDeep Inelastic ScatteringDeep inelastic scattering is the name given to a process used to probe the insides of hadrons , using electrons, muons and neutrinos. It provided the first convincing evidence of the reality of quarks, which up until that point had been considered by many to be a purely mathematical phenomenon...
, jet physics, quark-gluon plasmaQuark-gluon plasmaA quark–gluon plasma or quark soup is a phase of quantum chromodynamics which exists at extremely high temperature and/or density. This phase consists of asymptotically free quarks and gluons, which are several of the basic building blocks of matter...
.
External links
- Particle data group
- The millennium prize for proving confinement
- Ab Initio Determination of Light Hadron Masses
- Andreas S Kronfeld The Weight of the World Is Quantum Chromodynamics
- Andreas S Kronfeld Quantum chromodynamics with advanced computing
- Standard model gets right answer
- Quantum Chromodynamics
-
